分行剪纸
常文武


分形听起来高深莫测,其实只当它是一种自相似的玩意就好了,如图所示就是谢尔宾斯基三角形和谢尔宾斯基地毯的立体效果图。
看过分形图后,想到要通过剪纸方法剪出分形,你一定会觉得难,
然而令人不可思议的是,通过此文介绍的方法,你不但可以剪出漂亮的分形图,而且分形图还是立体效果的呢!
那我们就开始吧!取A4纸一张,剪刀一把。
步骤:
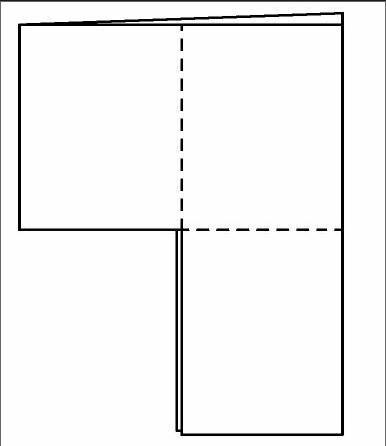
1.把A4纸的短边对齐短边折成双层,
2.在纸面上通过折纸找到水平和垂直的两条中轴线。
问题1:什么是分形?
李辰缘:分形图形一般是极不规则、分布不均,但在各种放大和缩小的尺寸上都有着近乎相似的形状。
冯烨:分形的单词是数学家曼德尔布·罗特根据拉丁文对其加以改造的,其含义是不规则的、琐碎的,我国就把它翻译成“分形”。
王伟业:通过查阅资料,我了解到分形几何是一门以非规则几何形态为研究对象的几何学,其研究的领域以及应用面无比广阔——它被广泛用于设计雕塑、绘画、服装、家居等各行各业。
问题2:你看过哪些有关分形的书,可以介绍给大家吗?
王伟业:《英国的海岸线有多长》给我留下深刻的印象,它是由20世纪70年代的著名数学家曼德尔布·罗特所写,其主要内容是探讨英国海岸线的长度,具有一定的思想深度,另外,张济忠的《分形》也不错,颇受广大读者喜爱,你若有兴趣,闲暇时也可翻阅一下。
3.用剪刀在折痕中点垂直于折痕剪开,刀口到中心处停下来,
4.把左下角的纸沉折到里面去,为此需再折两道痕同时改变上一道折痕的方向,效果图如下,
(注:沉折,折纸术语,就是将所指的部位,压入纸张内部,)
至此,我们来分析一下,剪开前的一道折痕现在成了4道短折痕:3道是山线,1道是谷线,
(注:山线就是凸起的折痕,谷线就是凹下的折痕。)
前面提到了自相似,现在看到的3道山线,每道都可当它是第一次剪开所碰到的那道折痕,因为它们的右边都有一个长方形也是竖直摆放的,只不过小了一号了。
明白了这一点,我们就可以继续下去了,如果你的剪刀够锋利,就可以两次搞定,如图,
问题3:你找到了哪些令你惊叹的分形图形,愿意拿出来与大家分享吗?
王迎新:西兰花便是一种分形图形。小编:看看还有什么?分形树叶、分形树。
问题4:说说你对分形的了解与体会。
王伟业:每一张分形图都是关神赋予我们最好的礼物,随着计算机技术的不断进步,越来越多唯关的分形作品被创造,但分形中最经典的,自然要数谢尔宾斯基的三角形了,它具有严格的自相似特点,相传在一个世纪前,在数学领域,人们惊奇地发现谢尔宾斯基三角形的面积居然为O!这令当时的数学家们百思不得其解,掌握了一定分形知识的你知道这是怎么回事吗?
问题5:谈谈你对于折纸、剪纸艺术与数学的看法,
吴蓝琨:折纸、剪纸都算是一种技艺,然而这种技艺与数学是分不开的。
接下来该怎么办你一定知道了,把刀口下方的3条山线沉折到里面,效果如下图,
毋庸赘述,上面的过程理论上显然是可以无限发展下去的,但实际上只能重复做有限次,下图展示了再通过两次细化后打开得到的效果。给它起个名字叫狮身人面像,像吗?
刘芳宁:有时一些数学问题,也能通过折纸、剪纸这种形象的方法来展现,
蒋卓珺:折纸、剪纸艺术很难离开数学规律,数学给人带来关和艺术。
王伟业:数学是灵魂、剪纸是肉体,正是由于数学与剪纸艺术那灵与肉的完美结合,使得数学由枯燥抽象的理论转变为主动、有趣、具体的视觉效果,化繁杂为简单,化抽象为具体,可以说剪纸搭起了数学与艺术的桥梁!
问题6:你还有什么想告诉小伙伴们的吗?
赵晟皓:记得以前看过一组图片,讲的是雪花的分形,众所周知,雪花是一个正六边形的轮廓,在六个角上会有类似树杈状的分支,其与整片雪花的形状是大致相同的,而在这分叉的分叉上也会有一个类似原雪花的形状,其也是一个分形图,分形这门学科十分强大,被推广到了许多领域,甚至是社科领域,乃至玄学,我认为其本身也有一定的哲学意味,象征着在某些地方局部事物与整体具有统一性,将剪纸与数学结合在一起,具有启发性。
王伟业:从无知到有知,从无形到有形,从曼德尔布·罗特刚提出分形概念到今天我们讨论谢尔宾斯基三角形,无不体现了我们人类的探索精神,这种不畏艰难、勇求上进的探索精神,不正是我们每个人都需要的吗?
陈子豪:多动手,多动脑,常思考所遇到新知识,尝试新方法,探索未知领域。
老师点评
分形几何源于20世纪70年代,发展时间虽短暂却速度迅猛,成为人人乐于研究的一门数学分支,在于其奇趣、美妙,引人入胜,分形是一个数学构造,且可以在自然界中被找到,这使得它们被划入艺术作品的范畴,把玩分形,欣赏分形,感悟数学,源于生活,表现生活,丰富生活。
——江苏省徐州市第一中学 张培强
谢尔宾斯基三角形是波兰数学家谢尔宾斯基在1915年提出的,它是分形图形的典型例子,同学们认识它可能还是学习了等比数列之后,通常我们作谢尔宾斯基三角形的方法是:先作一个正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,以此类推,用剪刀来剪出谢尔宾斯基三角形,更是博人眼球,同学们赶快拿起剪刀来试一试吧!要剪出文中的狮身人面像,除了按照文章中步骤剪,还要再加工,聪明的你能发现吗?
——江苏省江阴要塞中学 李红

