含齿根裂纹的非标齿轮啮合刚度改进算法及动态响应分析

张玲玉，徐颖强，许璠，秦宇飞，陈仙亮

（西北工业大学机电学院，陕西西安 710072）

含齿根裂纹的非标齿轮啮合刚度改进算法及动态响应分析

张玲玉，徐颖强，许璠，秦宇飞，陈仙亮

（西北工业大学机电学院，陕西西安 710072）

时变啮合刚度是齿轮系统动力学模型的参数激励，当齿轮出现齿根裂纹时，啮合刚度变化引起的动态响应特征是实现齿轮裂纹故障诊断的重要依据。以非标齿轮为研究对象，针对齿根裂纹故障对其时变啮合刚度的影响，建立考虑基圆与齿根圆不重合的变截面悬臂梁模型，提出利用改进势能法求解齿轮啮合刚度的计算模型，与原势能法和ISO 6336-1-2006进行对比分析，并计算齿顶高系数和顶隙系数改变时不同裂纹尺寸的轮齿刚度和齿轮时变啮合刚度；建立非标齿轮传动系统六自由度动力学分析模型，利用4-5阶Runge-Kutta数值法求解故障系统的动态响应。仿真结果表明改进势能法显著提高了非标齿轮时变啮合刚度的求解精度。齿根裂纹的存在使得非标齿轮综合啮合刚度明显减小，系统时域信号中存在周期性冲击响应，频域中出现调制边频带结构，这些均为齿轮系统故障诊断提供了理论依据。

齿根裂纹；时变啮合刚度；改进势能法；动力学分析

齿轮传动是工程中用于传递运动和动力的重要部件，相比于标准齿轮而言，非标齿轮具备设计参数灵活、重合度大、承载能力强及啮合传动平稳等优点，因此有更广泛的应用空间［1］。但是由于结构复杂，工作环境恶劣等因素，齿轮传动系统在整个生命周期内会出现多种失效形式，如果采用传统复形法进行齿轮疲劳试验，则需要反复拆卸和检测，过程极为繁琐、实时性弱。因此，通过齿轮传动系统动力学分析进行实时状态监测、寿命预估和故障诊断具有至关重要的意义。

国内外学者在齿轮时变啮合刚度方向做了很多研究。王龙宝、李亚鹏等［2-3］提出改进的石川公式算法，但仍然不能考虑轮齿故障因素的影响。Yang等［4］从能量角度出发首次提出了势能法计算齿轮时变刚度模型；Tian［5］补充了轮齿剪切刚度；Pandya等［6］探究了在不同轮齿参数下裂纹扩展路径对啮合刚度的影响。但是他们在计算轮齿刚度时，都没有考虑基体变形，而且假设轮齿为固定在齿轮基圆上的变截面悬臂梁，忽略了基圆与分度圆之间的能量。万志国等［7］提出了改进势能法，考虑了基圆与齿根圆不重合的问题，弥补了势能法的缺陷，但他们的研究对象为标准齿轮，对于非标齿轮的研究则相对较少。

本文以非标齿轮为研究对象，在前人研究成果基础上，采用改进势能算法计算无故障非标齿轮时变啮合刚度，并与ISO 6336-1-2006［8］进行验证分析；计算了不同非标因素下正常齿轮和不同裂纹尺寸齿轮的时变啮合刚度，模拟了故障齿轮系统的振动响应，得到齿根裂纹对时变啮合刚度及系统动态响应的影响规律，为高效地进行故障信号提取与诊断提供理论基础。

1　齿轮系统六自由度动力学模型

齿轮传动系统是一个弹性连续系统，包括齿轮副、传动轴、支承轴承、箱体、原动机和负载等零部件，在各种动态激励下会产生动态响应。

为研究齿根裂纹故障对齿轮传动系统的影响，本文忽略原动机和负载的影响，考虑综合啮合刚度和齿面摩擦系数等时变特征，用集中参数法建立了六自由度动力学模型，如图1所示。

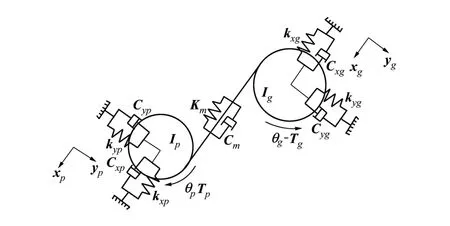
图1　齿轮系统六自由度振动模型

根据牛顿第二定律，结合集中参数动力学模型，建立齿轮传动系统六自由度运动微分方程。主、从动轮的扭转振动方程为：

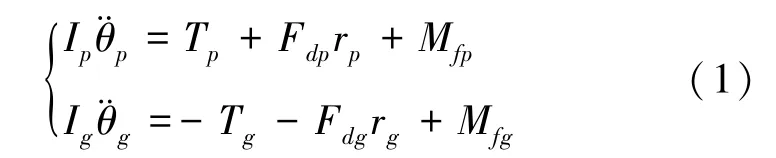
啮合线方向的力平衡方程为：

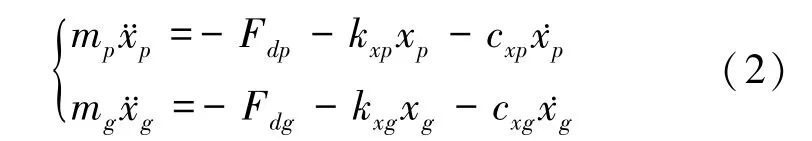
摩擦力方向的力平衡方程为：

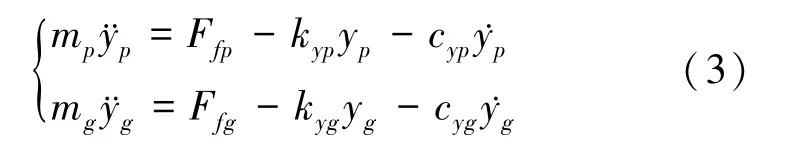
式中，mp、mg、Ip、Ig分别为主、从动轮的质量和转动惯量；kxp、kxg、kyp、kyg分别为主、从动轮的x方向和y方向的支撑轴承刚度；cxp、cxg、cyp、cyg为主、从动轮的x方向和y方向的支撑轴承阻尼；Fdp、Fdg为主、从动轮所受的动态啮合力；Ffp、Ffg为主、从动轮齿的滑动摩擦力；Mfp、Mfg为两齿轮相应的摩擦力矩，可由下式计算得到：

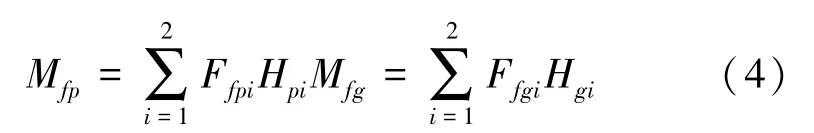
式中，i表示第i对轮齿（i=1，2）；Ffpi、Ffgi分别为主、从动轮第i个轮齿所受的摩擦力，Hpi、Hgi为相应的摩擦力臂，具体计算方法见文献［8］。

动态啮合力计算表达式为：

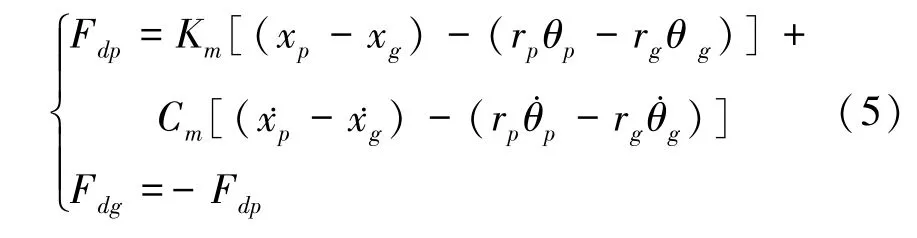
式中，Km和Cm为齿轮副时变啮合刚度和啮合阻尼。主、从动轮齿间的滑动摩擦力可表示为：

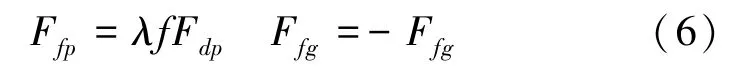
式中，f为时变摩擦系数，λ为齿面摩擦力方向系数，沿y正方向时取“+1”，反之取“-1”。

由公式（1）、（2）和（5）可知，齿轮时变啮合刚度为动力学模型中的弹性力项参数，因此确定啮合刚度是分析系统振动响应的前提。

2　时变啮合刚度改进算法

势能法计算时变啮合刚度的前提是将轮齿看做长度为d、固定在基圆的悬臂梁［9］，忽略了基圆与齿根圆之间势能，但是实际上齿轮基圆与齿根圆不重合，这将导致计算不准确，因此需对其进行修正。

据齿轮几何关系，基圆和齿根圆半径分别为

式中，m为模数，z为齿数，α0=20o。对于非标齿轮，按照齿顶高系数和顶隙系数的取值不同分为3种情况：①=1.15，c∗=0.25；②=1.25，c∗=0.25；③=1.25，c∗=0.28。若令rb=rf，则zlim=47， 50，51。因此，需要按照齿数z分情况讨论。

2.1z＜zlim的情况

当齿数z＜zlim时，rb＞rf，原势能法的悬臂梁模型是在基圆处的，因此改进势能法补充了储存在基圆与齿根圆之间的轮齿变形势能。此时，弯曲势能公式［7］为

式中，Ix1和Ax1为齿根过渡曲线部分距离基圆x1处的横截面惯性矩和面积，可由下式计算得到

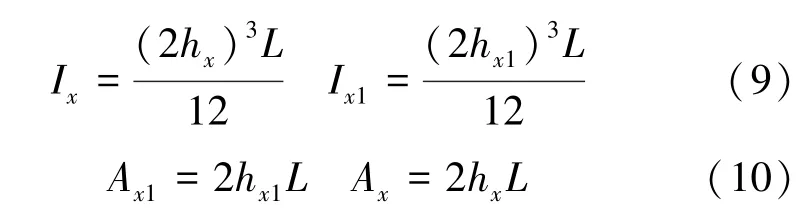
式中，R为齿根过渡曲线圆角半径，参数hx和hx1的计算表达式为

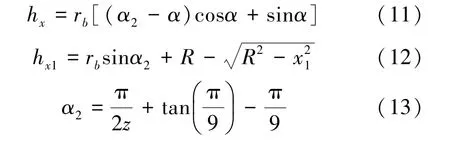
根据几何关系，我们可以得到

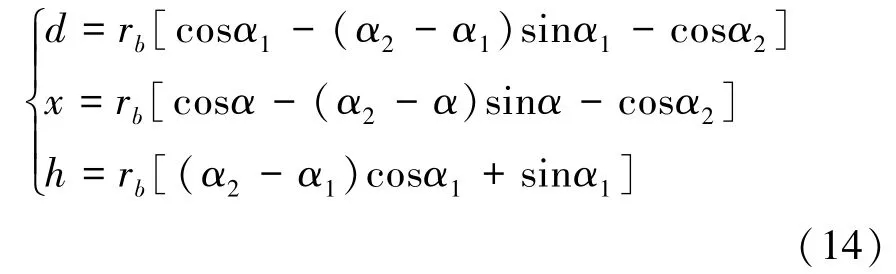
将公式（8）化简得到修正后的轮齿弯曲刚度为

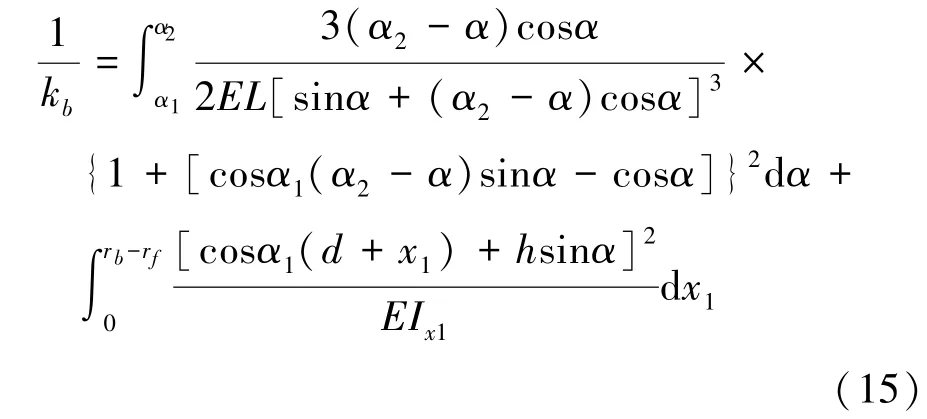
同样地，轮齿的剪切势能和轴向压缩势能为：

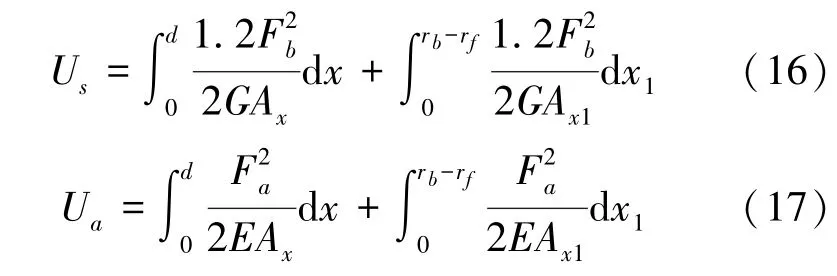
经过推导，将轮齿的剪切刚度ks和轴向压缩刚度ka修正为：

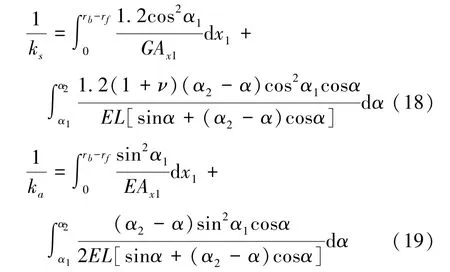
根据公式（15）、（18）和（19）可知，对渐开线轮齿来说，其弯曲刚度、剪切刚度和轴向压缩刚度仅仅是参数α1的函数，kb、ka和ks仅随啮合点位置变化而改变。

2.2z＞zlim的情况

当齿数z＞zlim时，rb＞rf，故应减去储存在基圆与齿根圆之间的轮齿变形势能。弯曲势能公式应修正为［7］

化简可得，

剪切刚度和轴向压缩刚度为：

f圆压力角和齿根圆压力角，θ和θf为二者相应展角。

2.3改进啮合刚度算法验证

为了验证时变啮合刚度改进算法的正确性，本文引入ISO 6336-1-2006标准，以求解单齿对最大啮合刚度与齿轮平均啮合刚度。单齿对最大啮合刚度为

式中，修正系数CM=0.8，齿轮毛坯系数CR=1，齿廓系数CB=1，β为螺旋角。cth为单齿对啮合刚度理论值，可以用下式计算

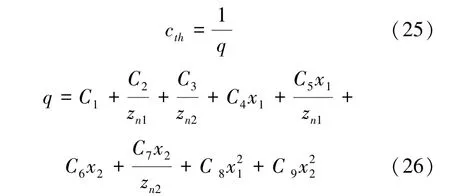
齿轮平均啮合刚度为

其中，各符号含义参见ISO 6336-1-2006标准。

以直齿圆柱齿轮为例，齿数Z1=30，Z2=36，模数m=5 mm，齿宽L=5 mm，弹性模量E=210 MPa，泊松比为0.3，=1.15，c∗=0.25。

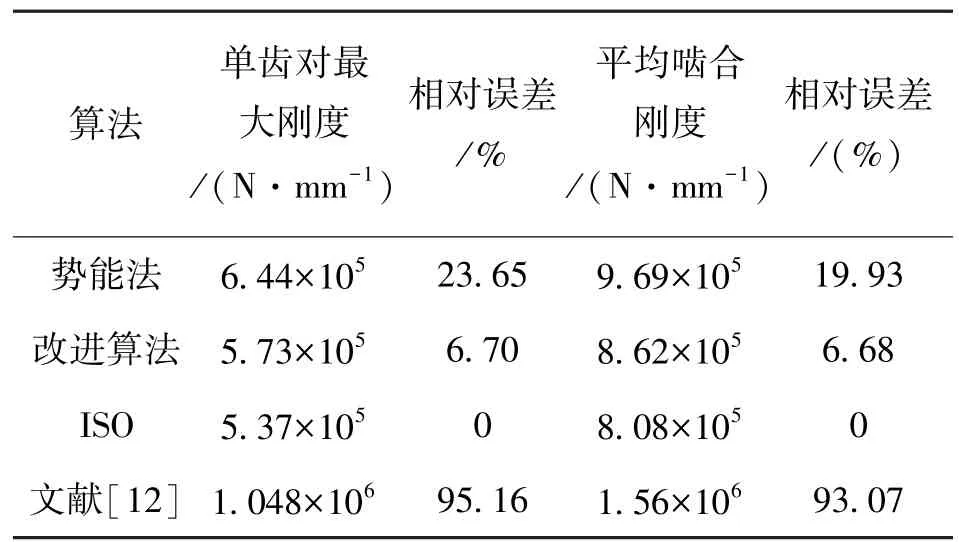
表1　与ISO相对误差比较

根据表1可知，本文改进算法所得结果与ISO结果十分接近，误差控制在7%以内。原势能法没有计算储存在基圆与齿根圆之间的势能，使得单齿对刚度值偏大23.65%，齿轮平均啮合刚度偏大19.93%。文献［10］忽略了齿轮基体的弹性变形，与势能法和改进势能法相比，其结果更偏离ISO。

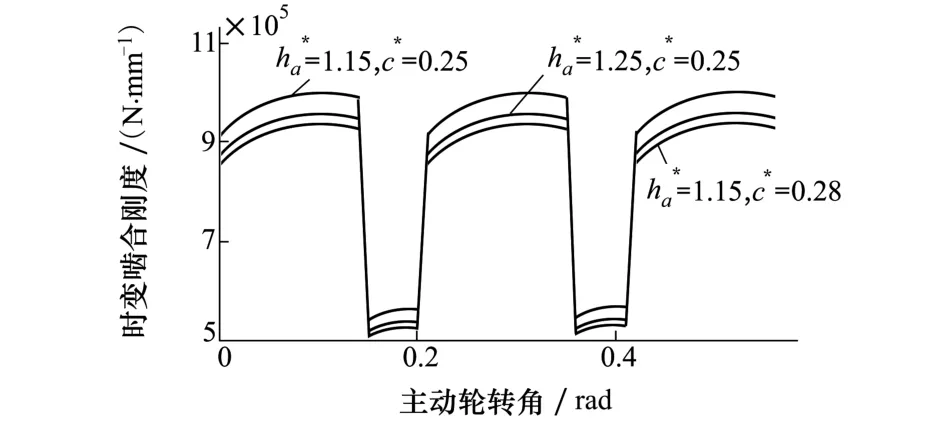
图2　不同参数的非标齿轮时变啮合刚度比较

图2为改进算法计算得到的非标齿轮时变啮合刚度结果。根据曲线可知，齿顶高系数和顶隙系数对啮合刚度影响明显。比较曲线1和2，当顶隙系数不变时，啮合刚度随着齿顶高系数的增大而减小。同样比较曲线2和3，啮合刚度会随顶隙系数增大而减小。

3　齿根裂纹啮合刚度计算

显然，接触刚度、轴向压缩刚度和基体刚度均不受轮齿裂纹影响，因而只需考虑弯曲刚度和剪切刚度的变化。对于齿根裂纹模型，我们应该分两种情况讨论：①当载荷F作用点未进入裂纹影响区域，即hx≤hc；②当载荷F作用点进入裂纹影响区域，即hx＞hc。因此，啮合轮齿储存的弯曲势能和剪切势能仍可由正常齿轮势能公式计算，但是惯性矩Ix和横截面积Ax需要分段，即

式中，hx表示齿廓线上距离基圆为x的点与轮齿水平中心线之间的距离，hc为裂纹根部到轮齿中心线的距离，由公式（30）求得，h0为裂纹起始位置高度。

因此，将公式（28）和（29）带入即可得到齿根裂纹轮齿的弯曲刚度和剪切刚度。图3为裂纹深度变化时，不同齿顶高系数和顶隙系数下的轮齿弯曲刚度和剪切刚度。

图3　不同裂纹深度的轮齿刚度

对于同一非标齿轮，轮齿的弯曲刚度和剪切刚度均随着裂纹深度增加而减小，而且这种影响在啮合初期更为明显。比较图4a）和图4b）可知，顶隙系数不变时，齿顶高系数越大，非标齿轮的弯曲刚度和剪切刚度越小，且弯曲刚度的下降幅度更大。

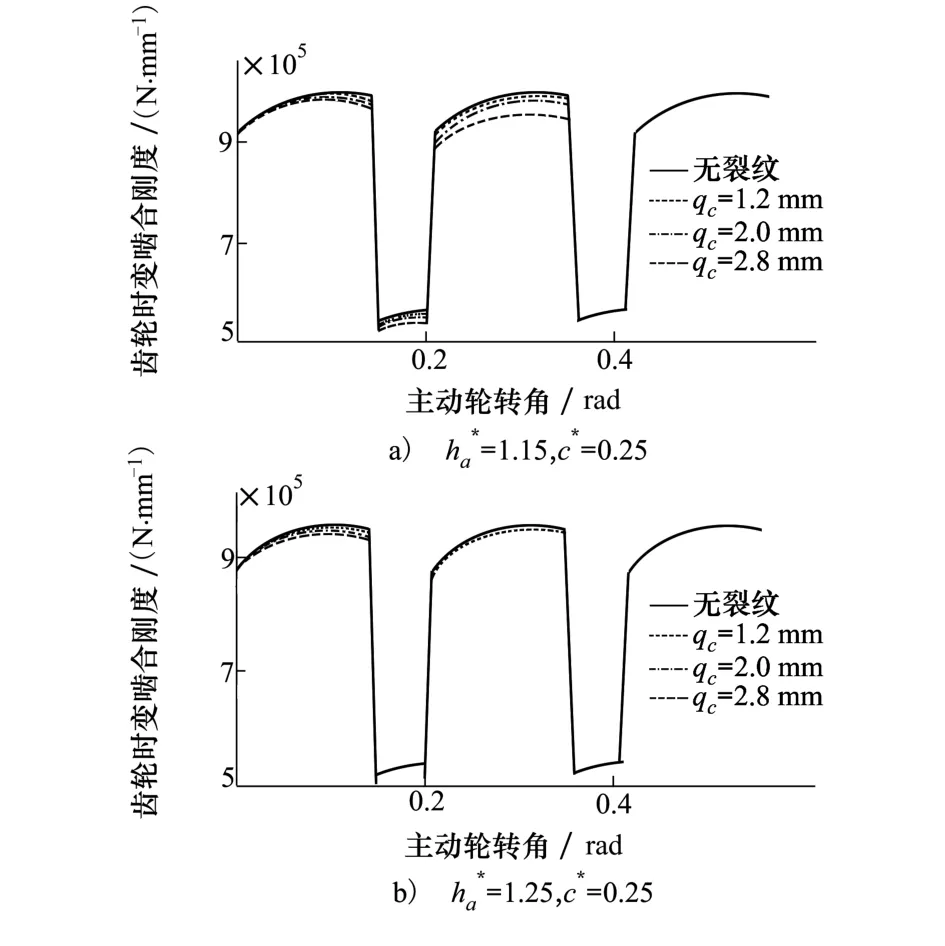
图4　非标齿轮时变啮合刚度

图4为不同裂纹尺寸下非标齿轮时变啮合刚度曲线。由于齿根裂纹的存在，故障齿轮副的时变啮合刚度值明显小于正常齿轮副啮合刚度。顶隙系数不变时，齿轮时变啮合刚度随着齿顶高系数增大而减小。

4　动态响应分析

选取输入转速为900 r/min，负载为2 750 N· mm，仿真时间为0.333 s，得到正常齿轮和裂纹深度为2.0 mm、角度为60°时主动轮X向位移的时域响应，如图5所示。

图5　主动轮X向位移时域响应

根据图5可知，正常齿轮传动系统（见图5a））的主动轮X向位移响应比较平稳，在某一值附近上下波动。当存在齿根裂纹时（见图5b）），主动轮的位移曲线出现以主动轮旋转周期0.066 7 s为间隔的异常波动，说明冲击正是由于主动轮齿根裂纹轮齿的啮合导致的。

图6为不同齿顶高系数下正常系统和裂纹齿轮系统的主动轮X向位移频谱图，是通过对时域波形作傅里叶变换得到的。观察图6a）、图6c）发现，在正常齿轮系统中，仅存在以啮合频率（450 Hz）及其倍频为中心的幅值谱，无调制现象。

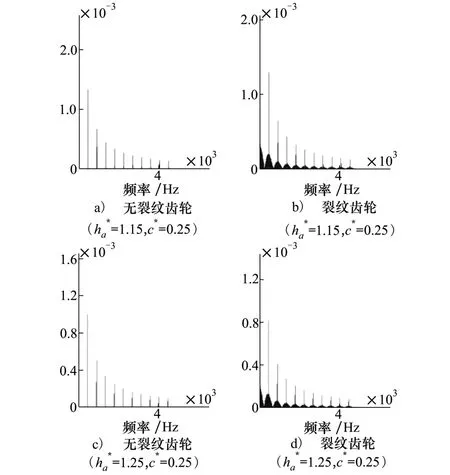
图6　主动轮X向位移频谱图

齿根裂纹系统（图6b）、图6d））相对于（图6a）、图6c））而言，在低阶啮合频率附近出现对称边频带，其幅值调制和频率调制现象较为明显，较高阶啮合频率附近也存在微弱的边频带结构。这是因为主动轮每旋转一周，裂纹轮齿就会参与一次啮合，产生一个脉冲激励。此外，齿根裂纹使得轮齿啮合刚度发生变化，因此除使得振幅加大外，还会使相位发生变化，即出现边频带。

5　结 论

1）本文考虑了基圆与齿根圆不重合因素，提出非标齿轮啮合刚度的改进算法，通过与原势能法和ISO 6336-1-2006结果对比分析，验证了改进算法的求解精确性。

2）通过求解齿顶高系数改变时不同裂纹尺寸的轮齿弯曲刚度、剪切刚度和时变啮合刚度，建立齿轮系统的动力学模型，采用数值解法研究了故障系统的振动响应特性，可以为进一步探索裂纹产生机理和故障诊断方法奠定基础。

［1］ 徐颖强，朱燃燃，于东洋，等.大顶隙长齿齿轮高弯曲承载能力关键技术研究［J］.机械强度，2014，36（5）：803-808

Xu Yingqiang，Zhu Ranran，Yu Dongyang，et al.Key Technology Research of Long Tooth and Large Bottom Clearance Gear with High Bending Bearing Capacity［J］.Journal of Mechanical Strength，2014，36（5）：803-808（in Chinese）

［2］ 王龙宝.齿轮刚度计算及其有限元分析［D］.南京：江苏大学，2007

Wang Longbao.Calculation and Finite Analysis of Gears Mesh Stiffness［D］.Nanjing：Jiangsu University，2007（in Chinese）

［3］ 李亚鹏，孙伟，魏静，等.齿轮时变啮合刚度改进算法［J］.机械传动，2010，35（5）：22-26

Li Yapeng，Sun Wei，Wei Jing，et al.Study on the Improved Algorithm of the Time-Varying Meshing Stiffness of Gear［J］.Journal of Mechanical Transmission，2010，35（5）：22-26（in Chinese）

［4］ Yang D，Lin J.Hertzian Damping，Tooth Friction and Bending Elasticity in Gear Lmpact Dynamics［J］.ASME J Mech Auto Des，1987，109（2）：189-196

［5］ Tian X.Dynamic Simulation for System Response of Gearbox Including Localized Gear Faults［D］.University of Alberta，Edmonton，Alberta，Canada，2004

［6］ Pandya Y，Parey.A Crack Behavior in a High Contact Ration Spur Gear Tooth and Its Effect on Mesh Stiffness［J］.Engineering Failure Analysis，2013（34）：69-78

［7］ Wan Zhiguo，Cao Hongrui，Zi Yanyang，et al.An Improved Time-Varying Mesh Stiffness Algorithm and Dynamic Modeling of Gear-Rotor System with Tooth Root Crack［J］.Engineering Failure Analysis，2014，42：157-177

［8］ Mohammed O D，Rantatalo M，Aidanpaa J O，et al.Vibration Signal Analysis for Gear Fault Diagnosis with Various Crack Progression Scenarios［J］.Mechanical Systems and Signal Processing，2013，41：176-195

［9］ 崔玲丽，康晨辉，高立新，等.含故障齿轮的动力学模型及振动响应研究［J］.振动与冲击，2010，29（Suppl 1）：40-42

Cui Lingli，Kang Chenhui，Gao Lixin，et al.Research on the Vibration Response and Dynamic Model of a Spur Gear System with Fault［J］.Journal of Vibration and Shock，2010，29（Suppl 1）：40-42（in Chinese）

［10］Wu Siyan，Zuo Mingjian，Parey Anand.Simulation of Spur Gear Dynamics and Estimation of Fault Growth［J］.Journal of Sound and Vibration，2008，317（3）：608-624

Improved Algorithm for Calculating Mesh Stiffness of Non-Standard Gear with Root Crack and Its Dynamic Responce Analysis

Zhang Linyu，Xu Yingqiang，Xu Fan，Qin Yufei，Chen Xianliang
（Department of Mechanical Engineering，Northwestern Polytechnical University，Xi′an 710072，china）

When a tooth crack failure occurs，the dynamic response caused by time-varying mesh stiffness changes plays a significant role in monitoring the operating conditions of a gear system and diagnosing its fault.We study a non-standard gear and the effect of tooth crack fault on the time-varying mesh stiffness.We establish the non-uniform cantilever beam model in which the misalignment between base circle and root circle is taken into account.The three gear mesh stiffneses calculated with the improved algorithm，the existing potential energy method and the ISO 6336-1-2006 Standard are compared to verify the improved potential energy method.The tooth stiffness and time-varying gear mesh stiffness with different crack sizes are calculated when the gear addendum coefficient and the tip clearance coefficient change.The 6-degeee-of-freedom dynamics analysis model of a non-standard gear transmission system is established，and the Runge-Kutta numerical method is used to analyze the dynamic response.The simulation results show that when the cracked tooth comes in contact，mesh stiffness decreases greatly and that the dynamic response presents a periodically impulse amplitude.Besides，modulation sidebands appear in the frequency domain；these results provide a theoretical basis for diagnosing the fault of a gear system.

calculations，computer simulation，dynamics，degrees of freedom（mechanics），dynamic response，errors，failure analysis，friction，gears，mean square error，monitoring，Runge-Kutta methods，stiffness；dynamics analysis，improved potential energy method，root crack，time-varying mesh stiffness

TH113；TH132

A

1000-2758（2015）06-0956-06

2015-04-01

国家自然科学基金（11072196）资助

张玲玉（1990—），女，西北工业大学博士研究生，主要从事结构疲劳强度与可靠性分析研究。