点焊机器人路径规划及应用

兰斌

摘要：针对目前白车身焊接机器人路径规划不合理的问题，总结归纳了不同算法的优点和不足，改进了贪婪算法容易进入局部最优的缺陷，并提出一种基于删除最大的距离的路径规划新算法。结合实际生产线车身侧围焊点布局，用两种算法作了对比分析，最后用DELMIA软件进行了实例验证。

关键词：白车身；路径规划；TSP问题；贪婪算法

前言

随着社会经济和科学技术的快速发展，焊接机器人技术不管是在研究领域还是工程实践领域都有了很大的提高。焊接机器人在白车身焊接上的运用，很大程度上提高了焊接质量，改善了工人的劳动条件，提高了生产效率。而点焊以其独特的成本优势使得它成为了目前国内的各大汽车组装厂的主要焊接方式。然而在实际生产过程中，传统的点焊机器人一般采用路采用在线示教方法对机器人的路径进行规划和仿真，由于工作任务和工作环境的复杂性，并且多台机器人还需避免相互干涉和碰撞，因此，实际工作中需对机器人反复调试，从而会导致机器人路径的设计工作量大、效率低，且不便于优化、无法并行工作[1]。本文在对点焊机器人和车身进行虚拟建模的基础上，提出基于删除最大距离的新型算法，并编写算法实现程序，在DELMIA软件仿真中实现点焊机器人路径自动规划，在很大程度上提高点焊机器人的路径规划设计效率，提高了点焊机器人的工作效率。

1.白车身焊接特点

焊接工艺是整车制造厂四个工艺之一，是白车身加工制造的重要环节，白车身焊接包括对发动机仓，前底板，后地板，侧围，顶棚和五门一盖等零部件或零部件总成的装配焊接。本文就侧围工位机器人点焊具有如下特点：

1.1工作环境复杂。侧围工位主要运用点焊机器人进行自动化焊接，焊接工位包括机器人群组，工装夹具，车身工件，传输装置等。机器人的活动范围是有限的，特别是在多台机器人在同一工位上执行操作的时候，往往会对机器人的路径规划造成很大的困难。

1.2焊点数量多。每个焊接工位上面有多台机器人，每台机器人负责的焊点一般二十个左右。

1.3使用的焊接方法多。包括电阻点焊、激光焊、CO2气体保护焊等等。其中电阻點焊因其独特的成本优势，良好的焊接性能，是目前国内整车厂中应用最广泛的焊接方式。

1.4对焊接技术要求高。对焊接产品有高的尺寸精度要求，对焊缝接头有高的性能要求，对批量化焊接生产有高品质的要求，对焊接过程有高节拍、高效率的要求[2]。

一台整车的焊点数有4000～5000个，每个人或是每台机器人负责的焊点一般二十多个，因此对车身焊点的路径规划显得很重要，一个好的路径不仅能节省人力、物力、财力，更重要的是能节省时间，提高效率和生产效益。

2.路径优化数学模型及优化算法

2.1.TSP旅行商问题基本思想和数学模型

旅行商问题（TSP）是组合优问题中典型的NP-完全问题，是许多领域内复杂工程优化问题的抽象形式。TSP问题是这样描述的：设有n个城市，一个旅行商从其中一个城市出发，最后回到出发的城市，其余n-1个城市，有且只能经过一次，目标是所经过的路径距离最短，这就是著名的旅行商问题（TSP）。用图论的语言来描述，正权图G=（V，E，W）中，包含图G中每个点至少一次的一条环路称为旅行商环路，一条具有最小权和的旅行商环路称为最佳旅行商环路，求最佳旅行商回路的问题称为旅行商问题（TSP）。而具有最小权和的哈密顿回路称为最佳哈密顿回路问题[3]。

旅行商问题（TSP）的数学模型描述如下：

设G=< V，E> 为赋权图，V={1，2，...，n}为顶点的集合，E为边的集合。各顶点间距离 已知（ >0， ，i，j V），并设

这里，S是V顶点集合的任意的一个子集，第一个约束意味着对每个顶点而言，仅有一条边进和一条边出，后一约束则保证了没有任何子回路解的产生。于是，满足上述约束的解构成了一条哈密顿回路。

2.2.改进贪婪算法及实现

求解TSP旅行商问题的解法很多，主要分为精确解法和近似解法两大类。精确算法能得到TSP的精确解，对于TSP的一些特殊情况，业已研究出一系列非常优美的结果，如：机器排序问题（Gilmore等，1964）、二分图情形（Lawler，1971）、平面TSP中的一些特例（Burkard，1989），等等。可解情形的结果都已经成为了成熟的定理。还有一些其他的精确算法如：线性规划算法、动态规划法、分之界定算法等。近似算法包括插入算法，最近邻算法，Clark&Wright算法，双生成树算法等。到了八十年代往后，出现了很多智能算法，如：神经网络算法，模拟退火算法，遗传算法，蚁群算法等[4]。上述算法各有各的特点和应用范围，精确算法能得到TSP的精确解，但是当维数n增大时，运算所用的时间成指数级增长，近似算法能较好的解决时间复杂度的问题，但是要牺牲一定的精度，智能算法则能在大型复杂工程问题时表现出其独特的优势，得到满足精度要求的解。

贪婪算法又叫贪心算法。贪婪算法（greedy algorithm）是一种解决最优化问题的近似方法[5]。它是一种逐步构建最优解的方法，在对问题求解时，总是做出当前看来最好的选择。，贪婪算法并不要求对所有问题都能得到整体最优解，而是某种意义上的局部最优解，在大量实际应用中，能得到问题的整体最优解或者是整体最优解的近似解[6]。

贪婪算法在每个决策阶段作出的决策不可更改，作出贪婪决策的依据称为贪婪准则（greedy criterion），也称贪婪因子。在路径规划中，路径的最小值即为贪婪因子。具体的算法流程如下：

Step1：输入n*n维距离矩阵D（对角元素为0的对称矩阵）和解矩阵X（和D矩阵同维数的0矩阵）。

Step2：选择任一顶点作为出发点，比较其他顶点与当前点的距离，选择最小距离的顶点相连。解矩阵X中对应连接的边赋值为1.

Step3：若最小距离的顶点已经在已连接的路径中，则赋值这个距离为无穷大，循环Step2.最终得到解矩阵X。

3.基于删除最大距离算法技术方案研究

总结以上算法，本文作者提出了一种基于删除最大距离的焊接机器人路径优化的近似算法。应用于较小维数的路径优化，新算法的时间复杂度为O（ ），能较快的收敛，并且思路简单，操作方便。基于删除最大距离算法与贪婪算法有相似之处，也容易产生局部解，经过改进，较小维数上能避免局部最优解的产生。在某种程度上，解要比贪婪算法更优。具有一定的应用价值。

基于删除最大距离算法流程如下：

Step1.构造一个n*n维距离矩阵D（对角线元素为0的对称矩阵）和解矩阵X（和D矩阵同维数的全1矩阵）。并对距离矩阵中元素从小到大进行排序。

Step2.选出最长距离，即最长边，两个顶点如果各连接的边数多于两条，则删除当前最长边，并把解矩阵中的当前位置元素赋值为0.循环直至所有满足要求的边都删除完为止。

Step3.在执行完Step2之后会出现两种情况：

3.1所有顶点都连接两条边，满足哈密顿回路，删除最长边，形成开环，得到需要的解矩阵。

3.2某一个或多个顶点连接边数多余两条或者形成局部环，形成局部最优解。

①某一个顶点或多个顶点连接边数多余两条处理如下。

找出当前顶点所连接边中最长的一条，在保证当前顶点连接边的另一顶点所连接边数大于一条时，删除当前边，直到当前顶点所连边数等于1为止。

②形成局部环处理。删除局部环中最长边。

③至此形成了两条以上的由数个顶点连接的开环。找出每条开环的端点，计算不在同一条环的各个端点之间的距离，选择最短的连接，直至所剩端点为2为止，形成一条开环链。得到需要的解矩阵。

基于删除最大距离算法流程图如下：

4.仿真实例验证

DELMIA数字制造解决方案可以使制造部门设计数字化产品的全部生产流程，在部署任何实际材料和机器之前进行虚拟演示。DELMIA软件由两个相互关联的独立软件DPE（Digital Process Engineer ）和DPM（Digital Process Manufacture）组成。

Robotics模块是一个基于物理的、可伸缩的三维机器人仿真解决方案。可用于对复杂的，多设备机器人工作单元进行建模和离线编程。利用Robotics可快速和图形化的构造各种应用工作单元作业，如焊接、喷涂、搬运、打磨和装配等。下图表示利用DELMIA/Robotics对车身焊接側围某工位的路径仿真画面。

本文的焊点分布来自某整车制造企业焊装生产线侧围总成工位SJ12机器人焊接焊点布局。焊接方式为点焊，生产节拍为70S。其中两层焊焊点10个，三层焊焊点7个。本文采用基于删除最大距离算法所求路径与改进贪婪算法和某整车制造企业生产线生产的路径进行对比，对比的标准是路径总和最短。

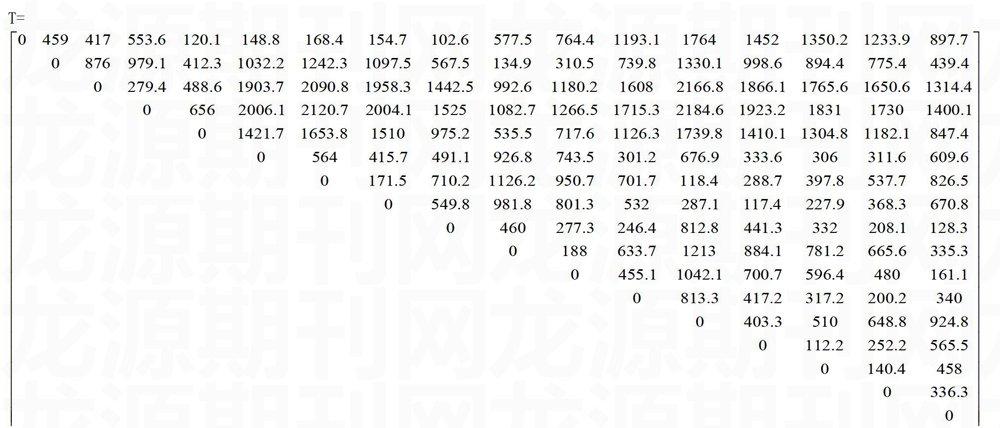
距离矩阵D是通过焊点坐标计算出来的，取D的上三角T矩阵如下：

基于删除最大距离算法的距离总长和贪婪算法距离总长对比，从表1中可看出，贪婪算法从1～17作为起始点，删除最大距离算法较贪婪算法更优。

5.结论

路径规划的算法有很多，针对不同的具体情况，各有各的优势和不足。本文解决了贪婪算法容易陷入局部最优的问题，并提出了一种基于删除最大距离的新算法。使用matlab编程实现，调用DELMIA/Robotics模块对汽车车身侧围某一工位点焊机器人路径进行了仿真，两种算法进行对比分析。分析结果表明，基于删除最大距离的算法能比较好的优化路径，满足路径规划的要求。

参考文献：

[1]张勇智，韩赞东.白车身装焊单元点焊机器人路径规划研究.机械设计与制造，2006.

[2]海江，罗生斌.白车身侧围工位焊接机器人路径优化研究[J].制造业自动化，2005，27（7）：35-38.

[3]管琳，白艳萍.用分支定界法求解旅行商问题.中北大学学报，2007，28（2）：104-107.

[4]马良.旅行推销员问题的算法综述.数学的实践与认识，2000，30（2）：156-165.

[5]Jean-claude Agnese，Pascal Brousse.Sch- eduling Techniques for a Constellation Visibil-ities[R].ASS98-303，1998.

[6]http：//baike.baidu.com/view/298415.htm？fromId=1628576.