港口起重机小车不同角度偏斜的接触应力分析

郑武军　吴姜玮

摘要：利用有限元软件ANSYS15.0对港口起重机小车轮轨接触进行弹塑性分析，用数值方法分析并比较轮轨正常工况和轮子水平面内发生小角度偏斜各个接触状态。结果表明：接触应力随偏斜角度增大而增大，发生点蚀破坏的危险增大。

关键词：有限元；起重机；接触应力

前言

随着各国经济贸易加强，带动了远洋运输业，码头越建越大，船舶的吨位不断增大，港口机械也朝着大型化、重型化的方向发展。这对起重机轨道和车轮的强度、承载能力和使用寿命提出更高的要求。

1.Hertz接触理论

对起重机车轮的设计[1][2]，传统的方法是采用赫兹公式计算接触疲劳强度，对车轮的许用轮压进行校核。德国人Hertz Heinrich 是接触理论的创始人。1881年在一定的假设条之下，他研究了两个弹性体的法向接触力学行为[3]。他的接触理论中假设条件归纳如下：1物体的接触表面连续光滑且无摩擦作用；2接触点附近的物体曲率半径是连续的常数；3接触斑的特征半径远小于接触物体的特征尺寸，接触物体被近似看作弹性无限半空间；4接触斑成椭圆状，接触斑上的法向压力分布成半椭球状。

但Hertz线弹性接触理论局限于无摩擦表面和理想弹性体。实际工程中的起重机，由于其巨大的自重及起重量，使得车轮与轨道接触部分局部材料超过了屈服极限成为塑性。在运行过程中，由于滑动摩擦力的影响，接触状态在不断改变，从而使车轮系统产生非线性的响应，这是典型的接触问题。有限元方法是目前解决复杂工程结构问题目前最有效的方法，它不但可以解决复杂的弹性接触问题，而且可以解决弹塑性接触问题。

2.轮轨接触有限元模型

在有限元方法中，接触问题是一种高度非线性问题[4]，即有接触面积变化而产生的非线性以及有由于接触压力分布变化而产生的非线性，也有由于摩擦作用而产生的非线性。因此求解过程需要较大的计算资源和时间，为了节约资源，可以只建立车轮的下半部分，并去掉车轮轮缘和倒角简化模型。本研究选取直径为500mm的双轮缘车轮SYL500和QU80型铁路轨道的接触，接触类型为线接触，按照起重车轮和轨道的尺寸建立模型，选用20节点的实体单元SOLID95。本模型由于主要研究接触区域的应力，因此对接触区域进行局部细化。模型中材料参数：弹性模量E为210GPa，泊松比为0.3，密度为 ，重力加速度为 ，摩擦系数为0.3。

由于轮轨接触变形时会有一定的滑动，故选用CONTACT174单元创建接接触面覆盖在车轮外径上，使用TARGE170来创建目标面轮轨上表面上，两者组成接触对，选用增广的拉格朗日求解算法求解。

将钢轨底面所有节点的自由度全部约束，钢轨的纵向线位移约束；同时在车轮上表面中心建立局部坐标，耦合其端面节点的法向自由度，防止局部自由度过大，使得ANSYS无法求解，约束车轮外圆与上表面的交线的纵向线位移，在施加载荷时，对载荷做等效处理，将载荷作用在平面上，即对车轮施加面载荷，这种加载方法对于结果的精度不会产生很大的影响。

3.计算结果比较分析

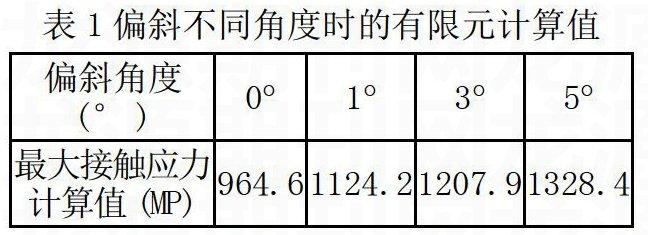
根据Hertz理论，可以计算出500KN作用力下，该模型无偏斜时轮轨接触时理论接触应力最大值为938.5MP；由图3可以看出轮子无偏斜时，最大接触应力为964.65MP，与理论值的相对误差为2.55%。

由表1可以看出当在500KN作用力下，轮子水平面内发生1°偏斜时最大接触应力为1121.81MP，与正常工况相比，接触应力增大了16.55%；轮子在水平面内发生3°偏斜时，接触应力最大值为1124.2MP，与正常工况相比，接触应力增大了25.2%；轮子在水平面内发生5°偏斜时，接触应力最大值为1328.4MP，与正常工况相比，接触应力增大了37.7%。

4.结论

（1）该模型的有限元计算结果是准确的，误差在工程容许范围之内，所以用有限元模型来模拟分析是合理的。

（2）轮轨接触时为线接触，接触斑近似为一矩形，最大接触应力出现在接触斑的两端部。

（3）轮子发生偏斜时，系统会承受更大的应力，且角度越大，接触应力越大，发生点蚀破坏的危险增大。所以起重机工作时应随时检测轮子的偏斜状态，调整到正常工况下工作。

参考文献：

[1]孙枫.港口起重机设计规范.北京：人民交通出版社，2007.8

[2]中华人民共和国国家标准局.GB3811-83.起重机设计规范.北京：中国标准出版，1983.08

[3]Johnson K L.著 徐秉业等译.接触力学北京：高等教育出版社，1992

[4]张洪伟，高相胜，张庆余.ANSYS非线性有限元分析方法及范例應用.北京：中国水利水电出版社，2013.4