基于随机效应的红松人工林一级枝条动态生长模型

朱万才 贾炜玮

摘要：基于孟家岗林场60株人工红松955个标准枝数据，使用非线性混合效应模型的相关理论和研究方法，分别考虑样地效应、单木效应和枝条效应，利用S-Plus软件中的NLME模块建立了红松人工林一级枝条动态生长模型。结果表明：红松人工林一级枝条基径和枝长的最优生长模型分别为Gompertz和Richards方程；随着随机效应尺度的减小（样地一单木_+枝条），混合模型的模拟精度逐渐提高，枝条基径和长度最优混合模型分别较基础模型提高约30.0%和2.4%，32.7%和6.6%以及50.1%和24.6%；基于枝条效应的基径最优混合模型不需进行误差项的校正，而枝条长度混合模型采用ARMA（1，1）时间序列结构可有效消除模型的异方差问题；独立检验结果表明枝条基径和长度最优混合模型的决定系数与基础模型相比增加了0.1左右，而平均误差绝对值和均方根误差均显著减小，说明非线性混合模型较传统非线性模型更适合于描述红松人工林一级枝条的生长过程。

关键词：红松人工林；枝条生长；非线性混合模型；方差协方差结构

中图分类号：S718.55

文献标识码：A

文章编号：1001-005X（2015）04-0026-07

树冠结构是林木自身遗传因素及其与周围环境长期交互作用的结果。研究树冠结构对评价林分（单木）健康、森林场景（林分、单木）可视化、制定合理经营措施等都具有重要意义。 研究树冠结构就是通过对树冠各结构因子的大量统计，找出它们之间的相关关系并且进一步分析潜在规律。随着研究方法和数据获取手段的不断进步，可将其大致分为4个阶段：①着重分析和比较树冠各结构变量及其空间分布状态，这一阶段主要采用定性的方法，枝条各个因子的空间分布状态；②根据临时样地上获取的资料，采用线性或非线性回归模型建立树冠各结构因子预测模型，虽然这类方法的研究历史较长，但由于从临时观测样地上获取枝条生长动态数据较为困难，因此该类方法对于树冠动态预测模型的研究较少；③利用树干解析、枝解析技术，仍然采用传统线性和非线性模型来研究树冠各结构因子的预测模型；④利用混合模型研究树冠结构因子的预测模型，与传统的回归模型相比，混合模型能够很大程度上提高模型的预估精度。

红松（Puzus koraiensis）是我国首批国家二级保护植物，由于其具有产量高、材质好、用途广、分布广以及耐严寒等特点，同时也是我国东北小兴安岭、长白山林区天然林中主要的树种组成。红松人工林也已成为我国东北地区主要的生态系统之一。但目前对红松人工林枝条动态生长预测的研究则鲜有报道。为此，本研究以黑龙江省佳木斯市孟家岗林场的红松人工林为研究对象，采用非线性混合模型分别研究不同尺度效应（样地、单木、枝条）对枝条基径和长度生长模型拟合精度的影响，在此基础上采用时间序列结构和异方差校正函数对模型误差项的方差协方差结构进行校正，以期为红松人工林树冠结构的动态预测提供科学依据。

1 研究区概况与方法

1.1 研究区概况

研究区域位于黑龙江省佳木斯市孟家岗林场（130°32'42"-130°52'36"E.46°20'30"-46°30'50"N），总经营面积1.63×104h㎡，总蓄积1.41×10⁶m³，森林覆盖率80.4%。该区年平均降雨量为550mm，年日照時数1955h，无霜期120d；区内最大河流为柳树河，属松花江水系；地带性土壤为暗棕壤，非地带性土壤为白浆土、草甸土、沼泽土以及泥炭土；植被属小兴安岭一老爷岭植物区的张广才岭亚区，其中天然林面积3.60×l0³hm²，蓄积4.07 xl0⁵m³。孟家岗林场森林资源丰富，既有天然林也有非常丰富的人工林，但总体上来说以人工林为主。人工红松在该地区有着非常广泛的分布，其果实具有非常高的营养价值，因此本研究以孟家岗林场红松人工林为研究对象。

1.2 数据收集

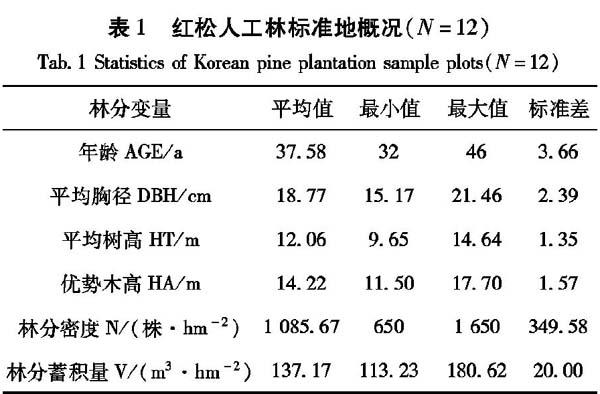
在对全区森林资源全面踏查的基础上，于2010年7月～8月在孟家岗林场不同年龄、不同密度、不同立地的红松人工林中选择有代表性的林分共设置12块固定标准地。样地面积一般为0.06h㎡，最大为0.09h㎡，采用5mx5m的相邻网格进行调查，以每个网格为调查单元。每木调查因子包括树种、胸径（DBH）、树高（HT）、冠幅（CIV）、活枝高、死枝高和坐标XY等，各个测量因子的详细统计表见表1。在研究区域内首先进行标准地的设置，在每一块标准地内选取能够反映整体水平5级标准木。对标准木进行伐倒后进行枝条解析，按照枝条解析的原则和方法分别测定所有枝条的各个属性因子，并进行记录。在每轮枝内，根据枝条的基径、长度以及长势等信息选取标准枝，查数枝条基部截面确定枝条的年龄，用游标卡尺测定枝条基径年轮宽度（0.1mm），用钢尺测定枝条每年的累积长度（1cm）。对上述所有测定内容，按样地、样木、轮枝、枝条分级编号，把外业数据录入计算机，建立数据库，并进行基础数据整理。按系统抽样方法，将数据按8：2分为建模数据和检验数据，由于同一轮枝内枝条大小、生长的变化差异很大，因此本文所建立的枝条模型采用标准枝数据，将所有数据按照接近3：1的比例划分成建模数据和独立检验数据，详见表2。

1.3 研究方法

1.3.1 基础模型

绘制枝条基径和枝长平均年生长量、累积生长量与龄阶的散点图从而得出枝条的动态生长过程图，如图1所示。从研究结果可以看出，人工林枝条生长速率与年龄有着非常密切的关系，其年生长量随着枝条年龄的增加总体呈下降趋势，但其累积生长是一个典型的具有一个渐进值的S型曲线（如图1（a）所示）。因此，利用实测的48株样木的772个枝条基径生长数据分别拟合Logistic方程和Mitscherlich方程、Gompertz方程、Richards方程、Korf方程、Schumacher方程、Weibull方程等方程，通过R²、RMSE、MAE等指标确定最优模型。

1.3.2 混合模型

混合模型近些年来得到了非常快速的发展，在林业数学模型中应用广泛，对模型的固定部分和混合效应部分都能够进行很好的拟合。有关模型的具体理论目前在很多文献中都已经有详细的描述，本文不在进行赘述。

2 结果与分析

2.1 基础模型

利用SAS软件中的NUN模块对枝条基径和枝长的7个备选模型分别进行拟合，各模型的参数估计值及拟合统计量见表3。枝条基径和长度模型的各项拟合统计指标较为接近，这可能是因为枝条的生长不仅受到自身遗传因素的制约，同时外界环境条件（光照、林分密度和地形等）对其也有很大干扰，导致其不同级别树木、不同枝条的生长出现一定程度的扰动；同时，非线性函数估计方法通常是将原方程展开为泰勒级数，一定程度上降低了原方程的敏感性。对枝条基径模型，Gompertz方程的拟合效果相对最好，且模型检验（F=26717.0.P<0.0001）极显著，各参数均通过t检验，说明该模型对描述红松人工林一级枝条基径的生长规律有显著意义。而对枝条长度模型，Richards方程的拟合效果相对最好，模型检验（F=50136.9.P<0.0001）和参数t检验也均极显著，说明该式对于描述红松人工林枝条长度生长规律具有显著意义。

2.2 混合模型

基于不同尺度效应和随机参数的组合，利用S-Plus软件的NLME模型对枝条基径和长度的最优基础模型进行拟合。利用AIC、BIC、-2Log likeli-hood对模型的拟合优度进行比较，指标数值越小说明模型的拟合效果越好，采用似然比检验进行比較，差异显著性水平设为a=0.05。

2.2.1 随机参数效应

基于样地效应的枝条基径和枝长模型的随机参数组合及拟合结果见表4。对枝条基径模型，混合模型收敛的情况共有6种，具有不同随机参数个数的模型间差异显著（P<0.0001）；当参数a₀，a₁，a₂全部为随机参数时模型的拟合效果最好，较基础模型提高了约30.0%。对枝条长度模型，混合模型收敛的情况共有5种，具有不同随机参数个数的模型间差异显著（P<0.0001）；当参数a₀，a₂为随机参数时模型的拟合效果最好，但较基础模型仅提高了约2.4%。综上分析可知，林分因子对枝条生长具有显著作用。

从表5可以看出，当将单木作为随机效应时不同参数的组合同样能够显著提高模型的拟合精度。对枝条基径模型，混合模型收敛的情况共有6种，具有不同随机参数个数的模型间差异显著（P<0.0001）；当参数a₀，a₁，a₂全部为随机参数时模型的拟合效果最好，较基础模型提高了约32.7%。而对枝条长度模型，混合模型收敛的情况则仅有3种，具有不同随机参数个数的模型间差异显著（P<0.0001）；当参数a₀，a₂为随机参数时模型的拟合效果最好，但较基础模型提高了约6.6%。上述结果同样说明树木因子会影响枝条的生长过程。

当进一步将枝条尺度作为随机效应时，枝条基径和长度模型收敛数量明显降低，但模型拟合效果得到明显提高（见表6）。对枝条基径模型，混合模型收敛的情况减少为4个，但模型的拟合精度较基础模型提高了约50.1%。而对枝条长度模型，则仅有2个混合模型收敛，模型的拟合精度也提高约24.6%，说明枝条因素对其生长具有极其显著的影响。

2.2.2 误差项的方差协方差结构

综上分析可知，枝条基径生长模型在考虑枝条效应时模型的拟合精度明显优于样地效应（LRT=12706.5）和树木效应（LRT=10998.8）。为此，本文以具有随机效应参数o.，a2的混合模型为基础测试了CS、AR （1）、ARMA（1，1）共3种时间序列结构，但模型拟合均不收敛，因此本文不考虑枝条基径模型的时间相关性，即为确定考虑了枝条效应后的枝条基径生长模型是否还存在异方差问题，绘制了基础模型和混合模型的残差分布图（如图2所示）。并且图2（b）表示出估计的枝条基径残差值比图2（a）的残差值分布范围小的多。为此，最终确定的红松人工林枝条基径生长混合模型如下： 式中：m_ijk为第i样地j株解析木k个枝条的年龄； 为第第i样地j株解析木k个枝条第1年时的预测误差；其余参数和变量如前所述。该模型的拟合参数如下：

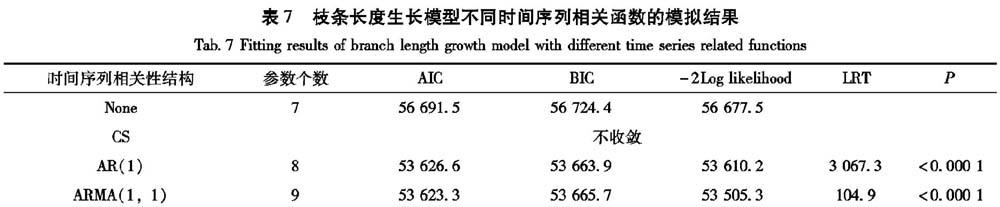
当把复合对称结构CS、自回归（AR（1））、自回归移动平均ARMA（1，1）分别加入以上得到的最优枝条基径混合模型中，模拟结果见表7。可以看出，当把cs结构加入到模型中，模型没有收敛；采用AR（1）和ARMA（1，1）结构比不考虑时间序列结构的精度高，而且ARMA（1，1）结构的3个评价指标最小，因此本研究采用ARMA（1，1）结构描述枝条长度生长的时间序列相关性。枝条长度生长的基础模型和最优混合模型的残差分布如图3所示。与基础模型相比，混合模型的残差分布范围更小，且模型的异方差现象得到有效消除，因此模型的异方差现象在本研究中不予考虑，即。因此最终确定的红松人工林枝条长度生长最优混合模型形式如下：式中：γ和p为时间序列结构ARMA（1，1）中的参数；其他参数和变量如前所述。该模型的拟合参数如下：

（1）固定参数：a₀=363.67；a₁=0.0967；a₂=1.2537。

（2）方差协方差结构参数。

（3）ARMA（1，1）结构参数：γ=0.7414；p=0.7556。

2.3 模型评价

为检验该混合模型的预测能力，根据各基础模型的模拟结果，计算12株检验样木的192个标准枝生长数据的随机效应参数μ_ij，进而计算出各标准枝的生长过程预测值，具体计算利用Mat-lab2010a软件实现，模型的各项统计指标见表8。可以看出，枝条基径和混合模型的预测精度均显著提高，其中枝条基径混合模型的确定系数提高了约0.08，平均绝对误差和均方根误差减小约1.2cm和1.7cm；枝条长度混合模型的确定系数提高约0.12，平均绝对误差和均方根误差下降约16. 27、25.44cm.说明混合模型能够有效提高红松人T林枝条生长模型的预测精度。

3 结论与讨论

本文定量揭示了不同尺度效应对枝条生长的影响，并采用时间序列结构和异方差校正函数对模型误差项的方差协方差结构进行了校正，使模型的拟合精度得到显著提高，得出以下结论：

（1）不同尺度的因子均对枝条的生长过程有显著影响。当分别将样地、单木和枝条作为随机效应时，枝条基径和长度最优混合模型的拟合精度分别较基础模型提高了约30.O%和2.4%，32.7%和6.6%以及50.1%和24. 6%。

（2）方差协方差结构的校正会显著影响模型的拟合精度。在本研究中，林业中常用的时间序列结构和异方差校正函数均不适用于枝条基径模型，有待于进一步探索或建立其他时间序列结构和异方差校正函数，而枝条长度模型采用ARMA（1，1）结构时已显著消除了模型误差项的自相关性和异质性。

（3）混合模型平均绝对误差和均方根误差则显著减小，说明混合模型技术能够显著提高枝条动态生长模型的预测精度。

b 但限于方法、数据和技术等方面的原因，本文在以下方面还有待于进一步研究：

（1）由于数据的限制，本研究的研究尺度有些受限，定量揭示不同尺度效应及其交互作用对枝条生长的影响，为综合确定合理的人工林经营措施提供理论依据。

（2）混合模型通过选用合适的结构能够有效消除这种现象，林业上应用最多的是采用UN、UN1和CS结构来消除残差异质性，AR（1）、ARMA（1，1）和CS结构消除残差的自相关性，虽然多数研究取得了较好的效果，但从本文的结果来看这些结构均不适用于枝条基径模型；Yang等建议在样本量足够大时，可考虑用TOEP（5）、POW（1）等更为复杂的结构来描述残差之间的关系，因此选用或根据数据的规律建立更合适的结构是混合模型今后应用中要解决的问题。