异径非标塔器运输鞍座设计与应力校核
黄德华
中石化宁波工程有限公司 浙江宁波 315207
随着我国石油化工行业的蓬勃发展,炼油产能不断提升,设备大型化趋势显著,特别是近十年来,国内直径10m左右,高度超过50m的大型非标塔器的已屡见不鲜。我公司作为中石化炼化集团公司大型非标设备制造基地,具备设备整体成型并通过港口或陆路运输至现场交货的实力。由于大型塔器直径大而且高,从工厂运往安装现场只能采用卧式运输,而在远途运输,特别是远洋运输中均采用鞍座支承。
非标塔器的大型化表现为高度和直径的增长,造成塔体在鞍座处的弯矩很大,而运输鞍座又不与筒体采用焊接连接,垫板不能起到筒体局部加强的作用,又因运输过程中的加速度的影响,壳体和鞍座受到的动载荷很大,如果不对塔体进行有效的校核,很容易造成运输中塔壳的失稳或破坏。
运输鞍座与JB4731-2005《钢制卧式容器》中的鞍座计算条件相比,此时容器为空载,不考虑内压作用,温度为常温,可不考虑腐蚀余量。因一端封头,一端裙座,鞍座一般不再对称分布,若筒体存在非等径状况,且要考虑运输过程中的动载荷和预紧力,因而不能再硬套原来的计算公式。本文就非等径塔体采用运输鞍座时的外载荷对塔器壳体的力学校核和失稳分析进行讨论。在讨论中使用的一系列公式,其中:
m—塔设备空质量,kg;
m1—塔器左端质量(含锥体质量),kg;
m2—塔器右端质量,kg;
q1,q2—支座1,支座2处附加了动载荷的单位长度载荷,N/mm;
L—塔器有效长度(从上封头2/3深度算起,至裙座底部),mm;
A1—左鞍座上封头2/3深度的距离,mm;
A2—右鞍座至裙座底环板下表面距离,mm;
L1—支座1至变径段小端的距离,mm;
L2—支座1至危险截面处的距离,mm;
V1—上封头切线至锥体大端间距离,mm;
V2—下封头切线至锥体小端间距离,mm;
D1,D2,D3,D4—支座1,支座2,危险截面处,锥体小端塔体的内径,mm;
δ1,δ2,δ3,δ4—支座1,支座2,危险截面处,锥体小端塔体的壁厚,mm;
B—鞍座宽度,mm;
H—鞍座底面距离至塔体中心的距离,mm;
θ—鞍座包角,°;
kV,kH,kR—运输时上下,前后,左右方向的动载荷系数,无量纲;
T1,T2—支座1,2的综合支反力,N;
T1’,T2’—支座1,2的竖直支反力,N;
T1”,T2”—支座1,2的侧向支反力,N;
M1,M2—支座1,2处的轴向弯矩,N.mm;
M3—危险截面处轴向弯矩,N.mm;
M4—变径段小端处轴向弯矩,N.mm;
σ1,σ2,σ3,σ4—支座1,支座2,中部危险截面,锥段小端处的轴向应力,Mpa;
[σ]t—常温下材料的许用应力,Mpa;
[σ]cr—常温下材料的许用压缩应力,[σ]cr=B(GB-150查取),Mpa;
τ1,τ2,τ、1,τ、2,—筒体在支座1,2截面的切向剪应力,Mpa;
σ5,σ6—支座1,2最低点周向应力,Mpa;
σ'5,σ"5,σ'6,σ"6,—支座1,2边角处周向应力,Mpa;
f—摩擦系数,根据不同材料选择,无量纲;
K—总安全系数,取值2/3;
Fm—最大摩擦力,N。
1 鞍座数量与位置布置
由于运输过程中很难保证支座的相对高度,并加以固定,对非等径塔器而言,如果使用三鞍座或更多鞍座的形式,很大情况下只能有其中某两个鞍座起作用,且这两个鞍座也不固定,属于静不定状况。该种受力状况异常复杂,可按照矩阵原理采用MATLAB列多方程计算式分析受力。本文仅按照材料力学基本原理针对双鞍座支承运输情况作分析。
为了改善受力状况,对于鞍座位置的设置,《钢制卧式容器》中要求鞍座在端部Rm/2和0.2L范围内,这是基于卧式容器的长径比一般都不太大(推荐3~6)的缘故。塔器的长径比一般都在15~20,甚至达到30~40,如果再按照《钢制卧式容器》的方法确定鞍座的位置,塔器在中间截面所有的弯曲应力将很高,远高于鞍座处的弯曲应力,这样就很难保证中间截面的安全。
如何来安排运输鞍座位置呢?由于塔设备的下封头在裙座上,到底部还有一段距离,有时也能利用封头的加强作用,再者,异径塔体的变径段(即锥体)一般也可作为刚性结构,相当于凸形封头,如果位置适当,也可加以利用,就是说可以使鞍座位置尽量靠近变径段和下封头,在其Rm/2范围内,至于具体怎样放置鞍座更合理,可以将鞍座设定在几个有代表性的位置,进行验算和比较后确定。
2 力学分析
2.1 受力分析
支座的受力情况和尺寸关系见图1。有效长度L从上封头2/3深度处算起,至裙座底部,A1,A2不一定相等,L1为支座1到变径段小端的距离,L2是支座1到危险截面处的距离,,,,,,,,分别为支座1,支座2和重心处及锥体小端塔体的内径和壁厚(扣除钢板负偏差,但不扣腐蚀余量);为鞍座宽度,为鞍座底面至塔体中心的距离,θ 为鞍座包角,所有尺寸单位为mm,角度单位为°,力的单位为N,下同。
设定卧式容器为承受两种均布载荷的连续梁,容器空载重量为mg,左右两端的质量分别为,(锥体部分计入大端)。容器总质量则由(式1)计算得出。

kV,kH,kR分别为上下,前后和左右方向的动载系数,以运输状况按经验选取,根据不同的运输方式动载荷系数一般取值如表1所示[1]。
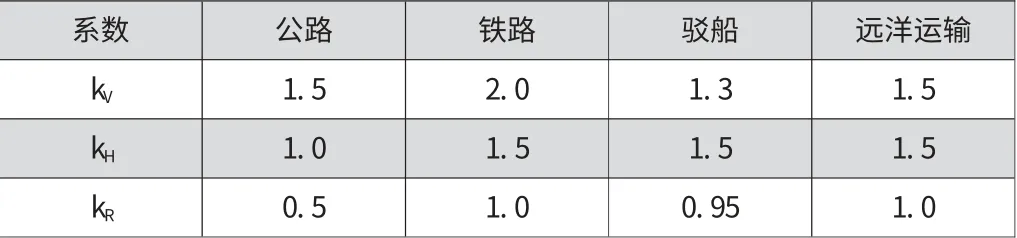
表1 运输动载荷系数
这样,容器承受以下外力:
轴向力kHmg,两个方向都要考虑;
侧向力,kRmg,考虑任一方向;
竖直方向,动载附加在两段均布载荷上,支座1端单位长度载荷可由(式2)计算;

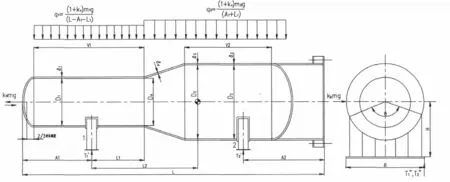
图1 塔器卧置尺寸、受力示意图
支座2端单位长度载荷可由(式3)计算。

2.2 支座反力计算
两支座反力分别为T1,T2。以支座2底部为支点,按力矩平衡理论[2]可得:
(1)轴向支反力
存在如(式4)的数学关系:
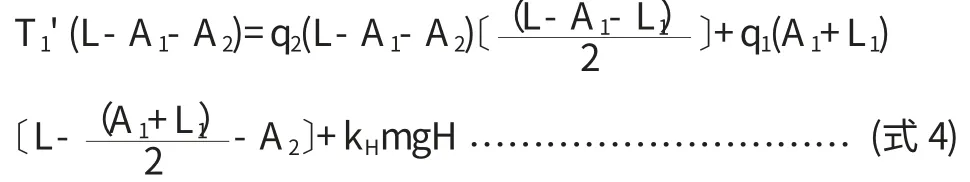
q1,q2见式(2)、(3),代入后,求得最大支反力:
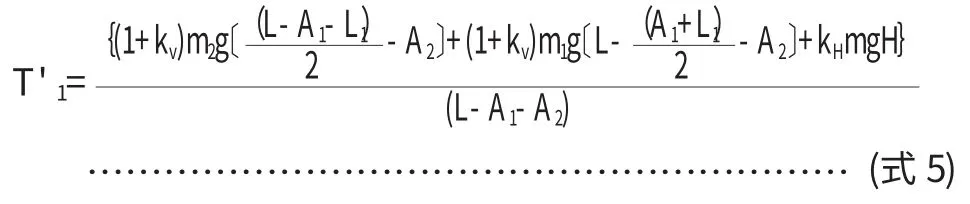
(2)侧向支反力
存在如(式6)的数学关系。

求得最大反力:

(3)综合最大反力
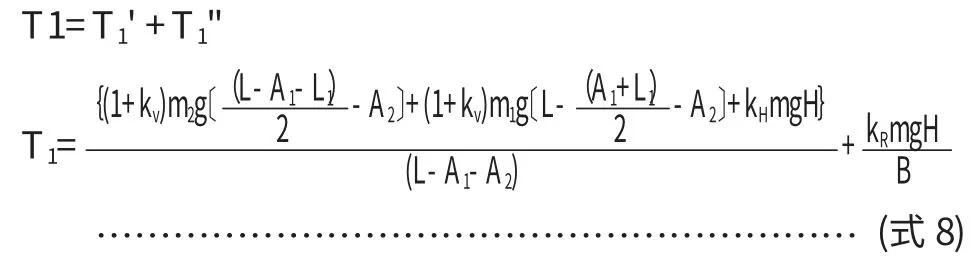
按同样方法可求得:T2=T2'+T2"
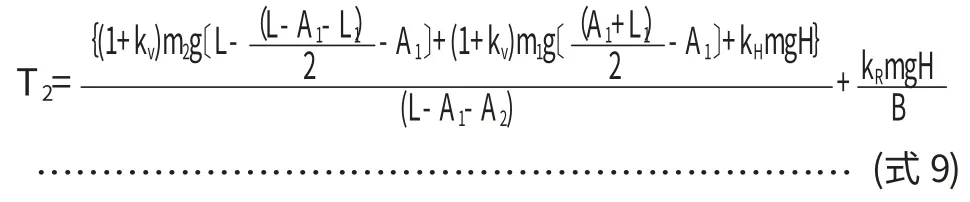
2.3 筒体轴向最大弯矩计算
塔器在运输过程中,由于侧向力对轴向弯矩没有作用,这里不考虑侧向动载,而轴向力方向不固定,它对各位置弯矩的影响按产生较大弯矩时的情况计算。轴向弯矩的最大值可能在两支座处,也可能在两支座跨距的中间某处。按力矩平衡理论[2]可按(式10)求出中间最大弯矩处的位置。

这里未考虑轴向动载的影响,因为轴向动载方向的不固定,它导致实际最大弯矩的位置也不固定,但和竖直方向的力相比,它由于力臂很短,实际对弯矩的影响很小,对最大弯矩位置的影响就更小。因此,这里确定最大弯矩位置时忽略轴向动载的作用,但在最大弯矩位置最大弯矩的计算中要加上该位置因轴向动载可能产生的最大弯矩。根据力矩平衡理论可求出:
(1)支座1处轴向弯矩
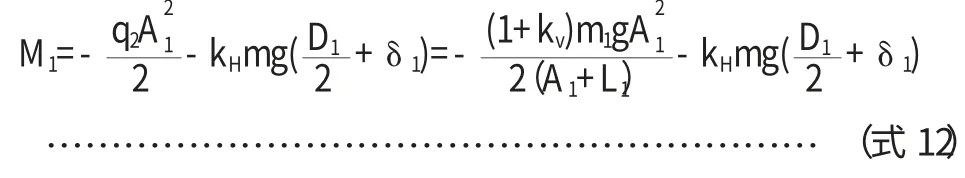
(2)支座2处轴向弯矩
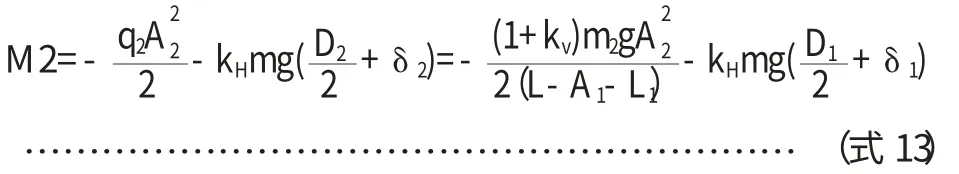
注:轴向动载的力臂不易确定,为方便计算,趋于保险,这里统一按大端取轴向动载的力臂。
(3)危险截面处轴向弯矩当L2≥L1时:
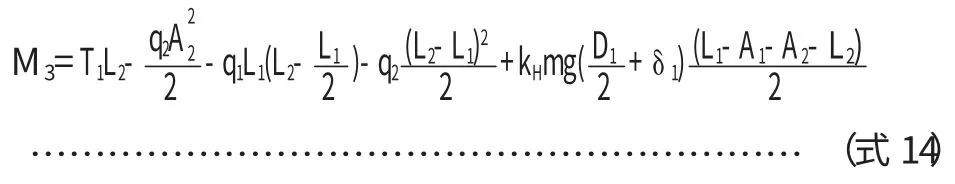
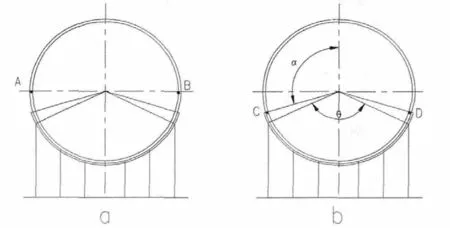
当L2 其中: 特别注意,如果计算的中部最大弯矩在大直径壳体处,此处并不一定就是中部的最危险截面,因为其截面的惯性矩比较大,在壳体处产生的弯曲应力就偏小,此时真正的危险截面还可能在变径段的小端。 因此,当L2 当圆筒在鞍座平面上或靠近鞍座处有加强圈或被封头加强时,即鞍座距离最近封头或锥体切线距离轴向应力σ1位于横截面最高点处(见图2a);当圆筒未被加强时,位于靠近水平中心线处(见图2b)。 图2 支座处圆筒轴向应力位置 3.1.1 支座处的轴向应力 (1)在支座1截面上,最高点处轴向应力: 式中,支座1处筒体截面的抗弯截面系数为: 因此, (2)在支座1截面上,最低点处轴向应力: (3)在支座2截面上,最高点处轴向应力: (4)在支座2截面上,最低点处轴向应力: 式中k1,k2取值查文献表[2]7-1。 3.1.2 危险截面处的轴向应力 (1)中部最大弯矩截面上,最高点处轴向应力: (2)中部最大弯矩截面上,最低点处轴向应力: (3)当L2>L1时,要考虑变径段小端截面上最高点处轴向应力: (4)当L2>L1时,变径段小端截面上最低点处轴向应力: 3.1.3 应力校核 计算出的轴向拉伸应力不得超过常温下材料的许用应力[σ]t,压缩应力不得超过材料的许用应力[σ]t和许用临界压应力[σ]cr。 [σ]cr=B,B可从文献[3]查取。 若圆筒在鞍座平面上有加强圈,其最大剪应力τ 位于截面的水平中心线处A、B点(见图3a);在安装平面内无加强圈或靠近鞍座处有加强圈,其最大剪应力τ 位于靠近鞍座边角处C、D(见图3b)。 图3 圆筒切向剪应力位置 3.2.1 支座处的剪应力 按未被加强取值文献表7-2。 (2)否则,壳体被加强,在支座1截面上切向剪应力: K3按被加强取值查文献[4]表7-2。 (3)还应校核封头或锥体处剪应力: K4按被加强取值,查文献[4]表7-2。为封头或锥体大端壁厚,扣除钢板负偏差,但不扣腐蚀余量。 K3按未被加强取值文献[4]表7-2。 (5)否则,壳体被加强,在支座2截面上的切向剪应力: K3按被加强取值文献[4]表7-2。 (6)此时还应校核封头: 但考虑底封头已被裙座加强,此计算可以免除。 3.2.2 切向剪应力校核 切向剪应力的校核条件为不超过材料常温下许用应力的0.8倍,即上述各式的结果必须满足: 对运输鞍座,垫板不起加强作用,且支座不与壳体焊接。 3.3.1 在支座1截面上周向应力校核 (1)最低点处: 式中 b2为支座1处筒体有效宽度;K5为仅与包角有关的系数,查文献[4]表7-3可知。 (2)鞍座边角处: 如果封头切线到锥体大端的距离≥4(D1+δ1), 式中,K6为与鞍座包角和是否被加强有关的系数,查文献[4]表7-3可知. 相反,如果封头切线到锥体大端的距离V1<4(D1+δ1), 3.3.2 在支座2截面上周向应力校核 (1)最低点处: 式中: 为支座2处筒体有效宽度;K5为仅与包角有关的系数,查文献表7-3可得。 (2)鞍座边角处: 如果底封头切线到锥体小端的距离V2≥4(D2+δ2), 相反,如果底封头切线到锥体小端的距离V2<4(D2+δ2), 3.3.3 周向应力的校核 支座处筒体最低点的周向应力不得超过常温下材料的许用应力,即σ5,σ6≤[σ]t鞍座边角处筒体的周向应力不得超过常温下材料许用应力的1.25倍,即 对运输鞍座,鞍座与筒体间轴向主要依靠摩擦力保持相对位置。由于运输中起动、加速和停止都会造成塔体的轴向动载,从而引起很大的惯性力,如果摩擦力不足,塔体将在鞍座中滑动。虽然塔体与载体(车或船)另有固定措施,塔体不致滑出,但也会造成塔体在鞍座中小幅度的串动,一来会使固定措施越来越松,甚至绷断;二来会造成塔体局部磨损,这都是不能允许的。因此有必要对摩擦力加以核算。为增大磨擦系数,通常在鞍座与筒体间增加橡胶等材质的软垫。 核算摩擦力时,支座反力不能再取最大值,侧向动载的影响可以不计,轴向动载使两鞍座反力一增一减,也不再计入。竖向动载按理应反向计入,但考虑竖向动载一般是瞬时的,与轴向动载不大可能会长时间同时发生,所以竖向动载一般也不计入,或者计入总的安全系数k中,此时: 事实上: 允许的最大磨擦力为: 式中,f为磨擦系数,可根据材料查相关资料,k为总的安全系数[5],建议取值2/3。摩擦力的校核条件为: 即: 一般情况下,塔体不会出现应力失效。但在一些直径大,高度很高和壁厚较薄的容器中,如果鞍座设置不合理,也很容易出现失效情况,特别是鞍座边角处的周向应力。 当轴向应力失效时,只能调整鞍座的位置。虽然改变鞍座及垫板的宽度也有作用,但影响很小。不过,只要位置调整适当,轴向应力应不致失效,实在必要时,可在塔体内外焊接筋板或垫板。如果切向力失效,应将鞍座放置在封头或锥体的加强区内,必要时还可以增加鞍座包角。 鞍座边角处周向力失效时,也可调整鞍座位置,使两支座反力更接近,或使支座位于能被锥体或封头加强的位置,其次是调整鞍座包角,角度越大,受力越好。必要和情况允许时,可在壳体相关部位增加垫板,与壳体焊接,或在支座处及其附近的筒体上焊接加强圈。关于有加强圈时周向应力的计算,可参见相关标准,由于篇幅关系这里不再赘述。 以上讨论都是关于在鞍座运输过程中塔体本身的受力校核,至于鞍座自身的设计,可以直接选用标准鞍座。根据以上求出的支座反力再乘上一定的安全系数(因同时还承受水平力)可作为选择鞍座依据的允许载荷。安全系数的取值依经验而定,一般不小于1.2。 工程实践操作过程中,鞍座运输的安全还取决于相关的方方面面。由于塔体能在鞍座中轴向移动,一定要将塔体和运输工具固定牢固,使其和运输工具成为一个整体。鞍座底部一定要有防止鞍座滑动的固定措施,为防止鞍座与壳体间可能发生的磨擦和振动;同时要在鞍座与壳体间增加软质垫片,塔体和与塔体直接接触的金属之间也要有防止擦伤和压伤的具体措施。与此同时还要保证所有措施在整个运输过程中不会失去作用,并在运输中加强检查,及时发现和纠正可能发生的任何问题。 1 DennisR.MossPressureVesselDesignMannal (ThirdEdition)Procedure 7 Transportation and Erection of Pressure Vwssels P365~P387. 2 《材料力学》刘鸿文 浙江大学出版社 第四版2004年10月 3 GB150.1~4-2011《压力容器》 4 JB/T 4731-2005《钢制卧式容器》 5 《机械设计手册》化学工业出版社2002年1月第4版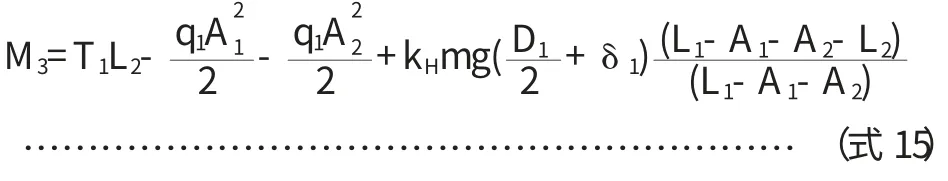
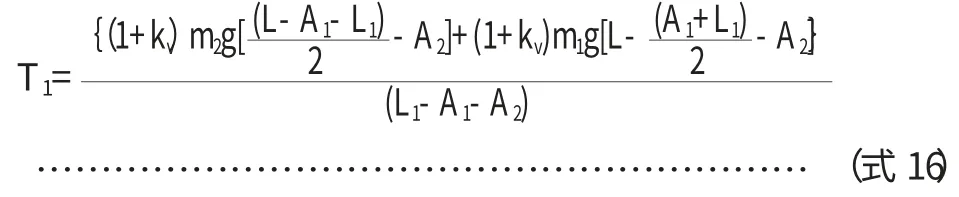
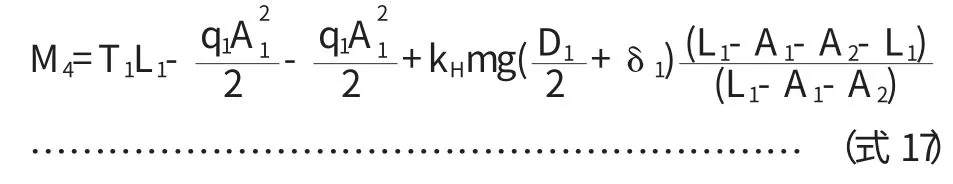
3 筒体应力校核
3.1 筒体轴向应力校核
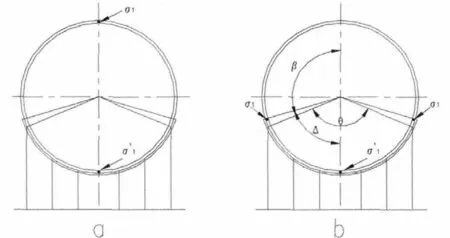


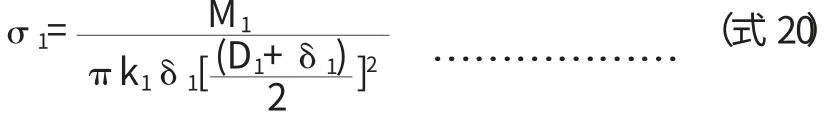
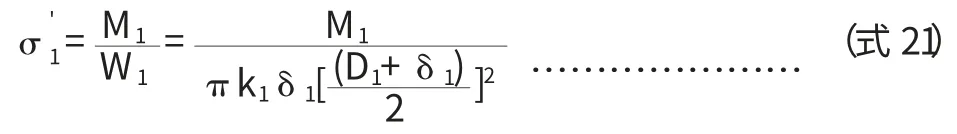
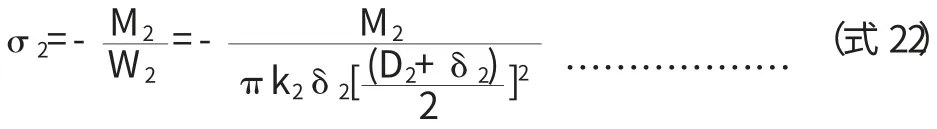
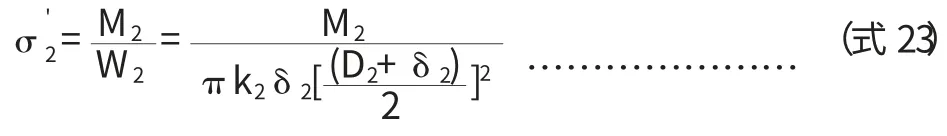
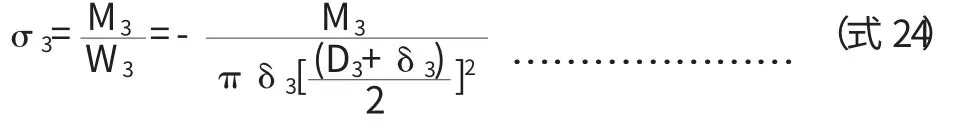
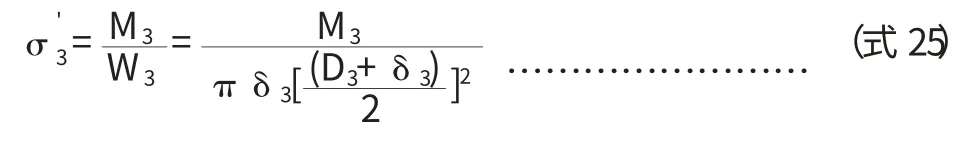
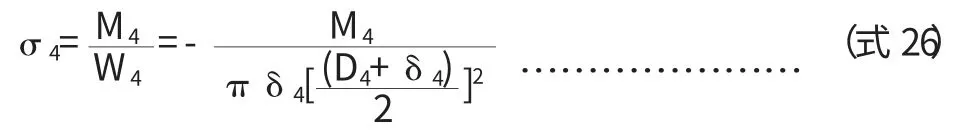
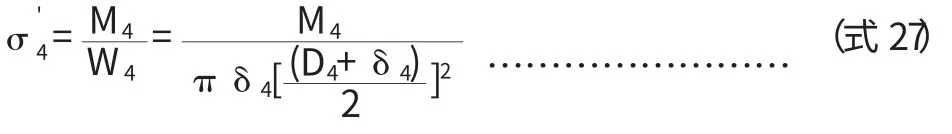
3.2 筒体切向剪应力校核







3.3 筒体周向应力校核

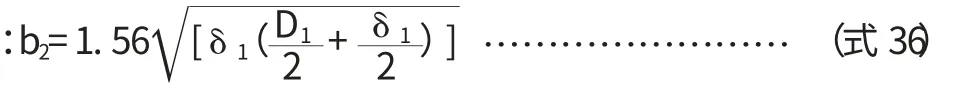

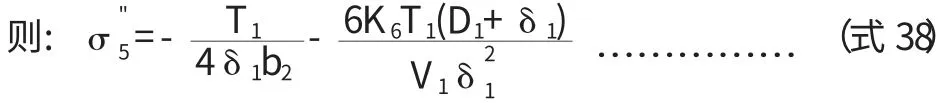

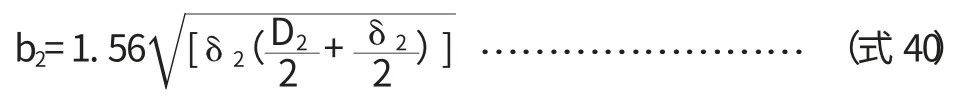

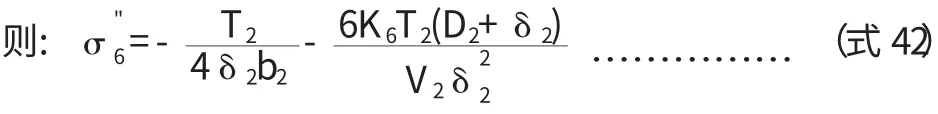

4 鞍座与筒体间轴向磨擦力的校核
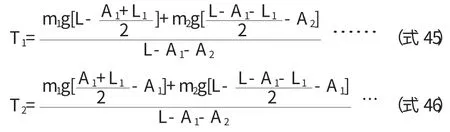

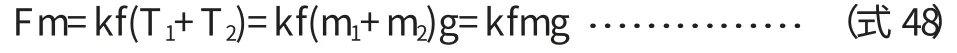


5 应力校核失效的处理
6 结束语

