最大比合并接收系统在n-Rayleigh信道下的性能分析
徐凌伟,张 浩,,刘 兴,王景景,Gulliver T A
(1.中国海洋大学信息科学与工程学院,山东青岛266100;2.加拿大维多利亚大学电子与计算机工程学院,维多利亚V8W 3P6;3.青岛科技大学信息科学与技术学院,山东青岛266061)
多输入多输出(MIMO)技术不仅使频谱得到了更好的利用,还使通信容量得到了提高[1],在下一代宽带无线移动通信系统中得到了广泛应用,尤其在信道建模、调制编码方面得到了广泛的关注[2-3]。在MIMO无线通信中,系统的性能受到了多径衰落现象的严重影响。分集接收技术可以减小多径衰落的影响,因此得到了广泛的应用。MRC(Maximal Ratio Combining)合并、EGC(Equal Gain Combining)合并和SC(Selection Combining)合并是3种主要的分集接收技术[4]。3种分集接收技术中,MRC性能最好,但是实践中不利于实现,SC和EGC性能相对差些,SC的实现程度最低。
W.Honcharenko等人通过实地测量,分别针对室内环境和城镇微小区环境,建立了适合移动通信的双瑞利(2-Rayleigh)分布模型[5-6]。文献[7]对2-Rayleigh分布的3种典型的传播场景进行了总结,在任何一种场景中,都可以用两个独立的Rayleigh分布的乘积来表示接收端信号的幅度特性。在2-Rayleigh分布的基础上,大量试验研究指出:当两个移动终端在相互通信时,其通信信道是通过其附近的散射体产生的n(n>2)个相互独立的Rayleigh衰落过程构成的,那么可以用n-Rayleigh分布来表示信道的幅度传播特性。n-Rayleigh分布在车联网移动通信、协作分集系统移动通信、无线传感器网络移动通信、卫星移动通信等方面得到了广泛的应用。文献[8]研究了n-Rayleigh分布的特点,得到了n-Rayleigh分布的概率密度函数(PDF)和累积分布函数(CDF),并详细分析了 n=3,4,5 时的情况。
从目前搜集的资料来看,研究文献主要是采用不同的分集接收技术,在独立的2-Rayleigh衰落信道下,研究系统的ASEP性能。文献[9-10]在独立的2-Rayleigh衰落信道下,基于MGF的方法,分别采用MRC等3种合并技术,得到了系统的ASEP性能表达式,并且分析了系统的中断概率(OP)。文献[11]在2-Rayleigh衰落信道下,采用MRC合并技术,利用MGF的方法,分析了系统的ASEP性能。
但是在n-Rayleigh衰落信道下,研究分集接收系统性能的文献很少。所以本文在n-Rayleigh信道下,针对分集支路的衰落幅度是否平衡的情况,基于MGF的方法,推导出了涵盖多种调制方式的ASEP性能的通用计算公式,并对不同系统条件下的ASEP性能做了数值仿真和分析,验证了分析结果的正确性。
1 系统模型
先从2-Rayleigh信道开始,然后扩展到n-Rayleigh信道。在这里,使用文献[9-10]中的2-Rayleigh信道模型,如图1所示。

图1 双瑞利信道模型
设a是符合2-Rayleigh分布的随机变量,a1和a2为两个独立的零均值循环复高斯随机变量,那么a=a1a2,其PDF为

式中:σ1
2,σ22分别为a1和a2的方差;K0(·)为修正的零阶第二类贝塞尔函数。a的平均功率[9]可以表示为

式中:E[·]表示求均值运算。
服从n-Rayleigh分布的随机变量Z可以表示为

式中:n是零均值循环复高斯随机变量的个数,则 Z的PDF[8]为

式中:Meijer’s G-函数[8]表示为
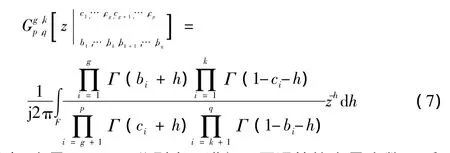
式中:变量g,k,p,q分别表示进行不同运算的变量个数;bi和ci是任意的实数。
假设接收端具有L个接收天线,则第i个接收天线的接收信号为

式中:Zi为相互独立的信道系数,服从n-Rayleigh分布;s表示发送端的发射信号,其平均能量为Es;W为加性复高斯噪声,其功率谱密度为N0。
由式(8)得,第i个接收天线的瞬时接收信噪比为

其平均接收信噪比为

则 ri的 PDF[12]可以表示为
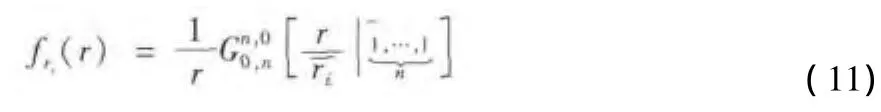
ri的 CDF[12]可以表示为

当接收机采用最大比合并时,接收端总的输出瞬时信噪比[13]可以为

在n-Rayleigh信道下,利用接收信噪比的MGF的方法分析最大比接收系统的ASEP,则ri的MGF为

为了计算式(14),使用文献[14]中的公式

式中:

所以将式(11)代入式(14)得

由于各ri相互独立,故由式(13)得rMRC的MGF为

1)当各分集支路衰落幅度不平衡时,可以表示为

使用文献[9]中的方法,计算各分集支路的平均接收信噪比,可以表示为

式中:W表示衰弱因子。
2)当各分集支路衰落幅度平衡时,各ri具有相同的均值,可以表示为

式(19)简化为

2 平均误码率分析
M-PSK、M-QAM、M-PAM等调制方式,进行相干解调时,系统的 ASEP[15]可以表示为

式中:Ed表示与调制方式有关的权重系数;D表示权重系数的个数;θd表示与调制方式有关的积分上限;φd,Vd,Λd表示影响因子。
2.1 M-PSK调制
采用相干检测的 M-PSK 调制时,D=1,Ed=1/π,θd=(M-1)π/M,φd=sin2θ/M,Vd=0,Λd=-1/2,所以系统的ASEP可以表示为
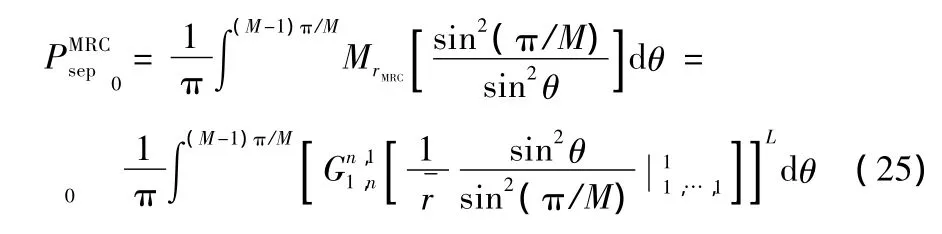
2.2 M-QAM调制
采用相干检测的M-QAM调制时,D=2,分为两种情况:

所以系统的ASEP可以表示为

2.3 M-PAM调制
采用相干检测的M-PAM调制时,D=1,Ed=2(M-1)/(πM),θd= π/2,φd=3/(M2-1),Vd=0,Λd=-1/2,所以系统的ASEP可以表示为

3 数值仿真
3.1 各支路衰落幅度平衡时的性能仿真
图2给出了在n-Rayleigh信道下,总发射信噪比对MRC接收系统的ASEP性能的影响。分集支路数L=1,2,3,n=2,调制方式是相干QPSK调制。由图2可知,理论值与仿真值之间的差距非常小,理论分析的正确性得到了证明。当分集支路数L一定时,MRC接收系统的ASEP性能随着发射信噪比的增加而不断降低,例如,分集支路数 L=2时,系统的ASEP在8 dB时为6×10-2,在10 dB时为3×10-2;当信噪比一定时,随着分集支路数的增加,系统的ASEP性能是不断改善的。例如,当 SNR=12 dB,分集支路数 L=1时,系统的ASEP是1×10-1;分集支路数L=2时,系统的ASEP是2×10-2;分集支路数L=3时,系统的ASEP是4×10-3。

图2 MRC接收系统使用QPSK调制的ASEP性能
图3 给出了在n-Rayleigh信道下,总发射信噪比对MRC接收系统的ASEP性能的影响。分集支路数L=1,2,3,n=2,调制方式是BPAM调制。由图3可知,理论结果与仿真结果相吻合,验证了理论分析的正确性。当分集支路数L一定时,MRC接收系统的ASEP随着发射信噪比的增加而不断降低,例如,分集支路数L=2时,系统的ASEP在8 dB时为1×10-2,在10 dB时为7×10-3;当信噪比一定时,随着分集支路数的增加,系统的ASEP性能是不断改善的。例如,当SNR=12 dB,分集支路数L=1时,系统的ASEP是4×10-2;分集支路数L=2时,系统的ASEP是4×10-3;分集支路数L=3时,系统的ASEP是6×10-4。

图3 MRC接收系统使用BPAM调制的ASEP性能
图4 分别在Rayleigh和2-Rayleigh衰落信道下,比较了分集支路数L=1,2,3三种情况的MRC分集接收系统的ASEP性能。在6种传输方式中,2-Rayleigh衰落信道下,L=1时,系统的ASEP性能最差,但当L>1时,采用MRC合并后,系统的ASEP性能是不断改善的。例如,L=2时,2-Rayleigh衰落信道下的性能已经优于Rayleigh衰落下L=1时的性能;2-Rayleigh衰落信道下,L=3的性能优于Rayleigh衰落下,L=2时的性能。当分集支路数L一定时,系统在Rayleigh信道下的性能优于2-Rayleigh信道下的性能。
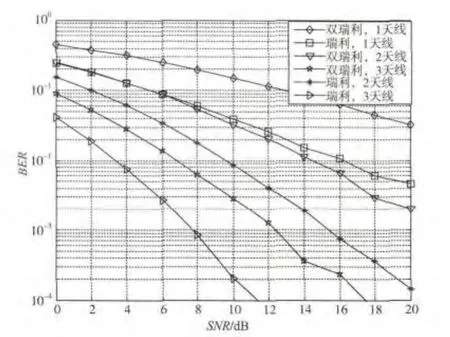
图4 MRC系统在不同信道下的ASEP性能比较
3.2 各支路衰落幅度不平衡时的性能仿真
图5 研究了分集支路数对MRC接收系统的ASEP性能的影响。分集支路数L=1,2,3,衰弱因子W=1。由图5可知,理论值与仿真值得之间的差距很小,理论分析的正确性得到了证明。当分集支路数L一定时,MRC接收系统的ASEP性能随着发射信噪比的增加而不断降低,例如,分集支路数L=2时,系统的ASEP在10 dB时为6×10-2,在12 dB时为4×10-2;当信噪比一定时,随着分集支路数的增加,系统的ASEP性能是不断改善的,例如,当SNR=12 dB,分集支路数L=1时,系统的ASEP是1×10-1;分集支路数L=2时,系统的ASEP是4×10-2;分集支路数L=3时,系统的ASEP是2×10-2。

图5 分集支路数对系统ASEP性能的影响
图6 研究了衰弱因子W对MRC接收系统的ASEP性能的影响。衰弱因子W分别取1,0.5,0,分集支路数L=2。由图6可知,理论值与仿真值得之间的差距很小,理论分析的正确性得到了证明。当衰落因子W一定时,随着发射信噪比的增加,MRC接收系统的ASEP不断减小,例如,衰落因子W=1时,在信噪比为8 dB时,系统的ASEP是9×10-2,在10 dB时,系统的ASEP是6×10-2;当信噪比一定时,随着衰落因子W的增大,系统的ASEP性能是不断变差的,例如,当SNR=14 dB,衰落因子W=0时,系统的ASEP是2×10-2;衰落因子W=0.5时,系统的ASEP是1.5×10-2;衰落因子W=1时,系统的ASEP是1×10-2。
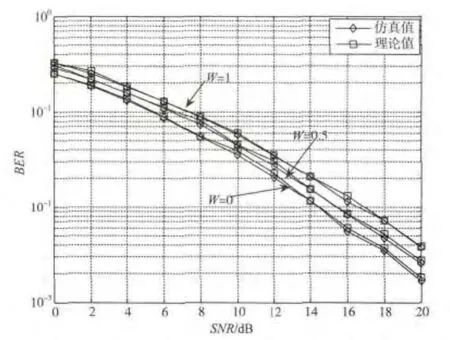
图6 衰弱因子对系统ASEP性能的影响
4 小结
本文在 n-Rayleigh信道下,基于MGF的方法,研究了MRC接收系统的ASEP性能,推导了MRC接收系统在n-Rayleigh衰落信道上采用相干检测的MPSK,MQAM,MPAM等调制方式的ASEP的精确表达式。然后针对分集支路的衰落幅度是否平衡的情况,分别做了仿真,理论分析值与仿真值差距很小,理论分析结果的正确性得到了验证。本文得到了如下结论:分集支路数和衰弱因子对系统的ASEP性能有着重要的影响。本文是在独立的信道下进行研究,但是独立信道在实际应用环境中,是一种非常理想的条件,因此在后续研究中,可以进一步研究相关信道对系统性能的影响。
[1] WANG K,WANG X D,XU W Q,et al.Coordinated linear precoding in downlink multicell MIMO-OFDMA networks[J].IEEE Trans.Signal Processing,2012,60(8):4264-4277.
[2]王振朝,张建平,种少飞.MIMO-OFDM系统ICI自消除改进算法[J].电视技术,2014,38(3):141-145.
[3]钱栋军,张静,顾夏珺.MIMO中继系统中基于失真信道的联合收发机设计[J].电视技术,2013,37(7):135-137.
[4]彭国祥,庄铭杰,林比宏.常见分集合并系统的性能分析[J].电视技术,2005,29(6):58-62.
[5] HONCHARENKO W,BERTONI H L,DAILING JL.Bilateral averaging over receiving and transmitting areas for accurate measurements of sector average signal strength inside buildings[J].IEEE Trans.Antennas and Propagation,1995,43(5):508-512.
[6] ERCEG V,FORTUNE SJ,LING J,et al.Comparison of a computer based propagation toll with experimental data collected in urban microcellular environments[J].IEEE Journal on Selected Areas in Communication,1997,15(4):677-684.
[7] SALO J,EL SALLABI H M,VAINIKAINEN P.Statistical analysis of the multiple scattering radio channel[J].IEEE Trans.Antennas and Propagation,2006,54(11):3114-3124.
[8] SALO J,El SALLABI H M,VAINIKAINEN P.The distribution of the product of independent Rayleigh random variables[J].IEEE Trans.Antennas and Propagation,2006,54(2):639-643.
[9]李兆训,曹文魁,梁波,等.双瑞利衰落信道下最大比合并性能研究[J]. 电路与系统学报,2012,17(3):88-93.
[10]李兆训,胡捍英.双瑞利衰落信道下双天线接收系统分集特性分析[J].西安电子科技大学学报,2011,38(4):160-166.
[11] UYSAL M.Maximum achievable diversity order for cascaded Rayleigh fading channels[J].IEEE Electron Letter,2005,41(23):1289-1290.
[12] GEORGE K K,NIKOSC S,P T M.N*Nakagami:A novel stochastic model for cascaded fading channels[J].IEEE Trans.Communications,2007,55(8):1453-1458.
[13] SIMON M K,ALOUINI M S.Digital Communication over Fading Channels[M].2nd ed.Hoboken,New Jersey:John Wiley &Sons Press,2005.
[14] ADAMCHIK V S,MARICHEV O I.The algorithm for calculating integrals of hypergeometric type functions and its realization in reduce system[C]//Proc.International Symposium on Symbolic and Algebraic Computation.Tokyo,Japan:IEEE Press,1990:212-224.
[15] YILMAZ F,KUCUR O.Exact performance of wireless multihop transmission for M-ary coherent modulations over generalized gamma fading channels[C]//Proc.International Symposium on Personal, Indoor and Mobile Radio Communications. Cannes,France:IEEE Press,2008:1-5.

