基于GPU并行计算的OMP算法

谈继魁，方 勇，霍迎秋

(西北农林科技大学信息工程学院，陕西杨陵712100)

随着信息技术、计算机技术及多媒体技术的快速发展，需要处理的数据量越来越大，而传统的Nyquist采样定理要求对信号的采样率不得低于信号带宽的2倍，这就需要有效的方法来提高对信号的处理能力。压缩感知(Compressed Sensing，CS)理论是Donobo与Candes等人在2006年提出的一种新的信号处理理论框架［1］。该理论表明，利用较少的信号值就可实现稀疏的或可压缩信号的精确重建，这使得其在信号处理领域中有着非常广阔的应用前景［2］。重建算法是CS理论的核心。在匹配追踪(Matching Pursuit，MP)算法的基础上提出来的正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法是经典的重建算法［3］，其沿用了MP算法选择原子的准则，不同的是OMP算法通过递归地对已选择的所有原子进行正交化处理，以保证每次迭代的最优性，从而减少了迭代次数［4］。

OMP算法提高了算法的性能，但在分解的每一步都对所选原子做正交化处理，增加了算法的计算复杂度［5］。针对这一问题，本文采用并行计算在图形处理单元(Graphics Processing Unit，GPU)上加速该算法，首先分析OMP算法的复杂度，找出影响其复杂度较高的部分，在GPU平台上设计其并行方案对算法进行优化，以提高OMP算法的运行速度。

1 OMP算法分析

令传感矩阵 Α=(α1，…，αn)，其中 αi∈Rm(R 表示实数集)是矩阵Α的第i列，称矩阵Α和向量αi分别为字典和原子。令y=Az，其中z在Ψ域(可逆变换矩阵)中k阶稀疏［6］。当迭代次数t≤k时，OMP算法计算步骤如下:

第一步，输入传感矩阵 A∈Rm×n，测量值 y∈Rm，稀疏度为k;令残差r=y，被选中原子的索引集i=Φ;

第三步，由i=i∪it更新索引集;

按照上述几步，对OMP算法的复杂度作如下分析:

1)投影:投影部分的实质是矩阵向量的乘法运算。残差r在原子上的投影可以表述为〈r，ai'〉/ai'2，〈·，·〉表示两个向量的内积，·2表示向量的l2模。为简化计算，令ρ =(a12，…，an2)T，则投影部分可以转化为 ATr./ρ，其中．/表示点除。由于矩阵Α的大小为m×n而残差r是大小为m的列向量，因此，投影部分的复杂度为Ο(m×n)。

2)选择最匹配的原子:从未选中的原子中选取与残差r投影绝对值最大原子的索引。字典Α每一行有n个原子，且k≪n，故本部分的复杂度为 Ο(n)。

4)更新残差:由于t≤k≪n2，因此相比于投影部分的复杂度，这一步的复杂度非常小甚至可以忽略。

基于上述分析可知，当k值比较小的时候，OMP算法的计算复杂度主要取决于投影部分，且其复杂度为Ο(m×n);而当k取值较大的时候，OMP算法的计算复杂度主要取决于矩阵求逆部分，其复杂度为 Ο(k3)。因此，影响OMP算法计算效率的关键步骤为投影部分矩阵向量相乘和更新权值部分矩阵求逆。

2 GPU简述

GPU是由流多处理器(Streaming Multiprocessor，SM)构成的，而流多处理器是由流处理器(Streaming Processor，SP)构成的。运行在GPU上的程序称为核函数。图1所示为GPU编程模型，GPU线程被组织成Thread-Block-Grid三层结构，每个 Grid包含若干 Block，每个 Block又包含若干个Thread。GPU运行时采用单指令多线程(Single Instruction，Multiple Thread，SIMT)执行模式，这意味着同一个SM中的SP执行的指令完全相同。GPU的存储器是由1个全局存储器和4个不同类型的片上存储器构成，分别为常量存储器、纹理存储器、共享存储器和寄存器［7］。寄存器是线程特定的，即每个线程只能访问自己的寄存器，而共享存储器是SM特定的，每个SM的所有线程都能访问这个SM的共享存储器。全局存储器、常量存储器和纹理存储器都可以被所有GPU的线程访问。常量存储器和纹理存储器都是只读的，使用它们可以减少所需要的内存带宽。全局存储器、常量存储器和纹理存储器的使用可以实现不同的优化，例如纹理存储器可以为特定的数据格式提供不同的寻址方式［7-10］。

图1 GPU编程模型示意图

本实验是在NVIDIA GTX480显卡上完成的，它由15个有效的SM构成，每个SM由32个SP构成。因此，该显卡总共含有480个处理器内核(Processor Core)。NVIDIA GTX480的每个SM包含64 kbyte的寄存器和48 kbyte的共享存储器，在运行时SM将寄存器平均分配给所有线程。此外，每个NVIDIA GTX480还包含1.5 Gbyte的全局存储器和64 kbyte的纹理存储器。

3 OMP算法在GPU上的并行实现

通过分析可知，影响OMP算法复杂度的关键步骤是矩阵求逆和矩阵向量相乘两部分。下面分别介绍基于GPU的矩阵求逆和矩阵向量相乘的并行计算，并给出OMP算法在GPU上并行实现的方案。

3．1 矩阵逆更新

由式(1)可知求解t×t大小矩阵逆的复杂度为 Ο(t3)。然而在OMP算法的每次迭代中，At是在上添加一列构成的，这表明可以使用矩阵逆更新算法［11］来求解矩阵的逆从而降低其计算复杂度。

式中:d和P的表述如式(3)和式(4)所示

为了进一步简化计算，作如下定义

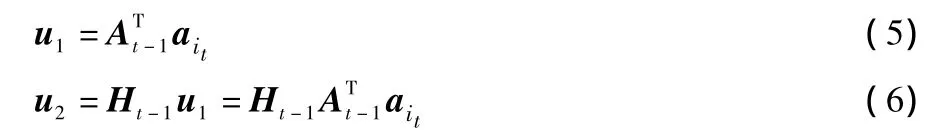
将d和P简化为式(7)和式(8)

由此，Ht的表达式可以简化为式(9)

3．2 矩阵向量相乘块算法

3．3 OMP算法的并行实现

要在GPU上并行实现OMP算法，需要在GPU上为输入变量分配内存。输入变量为和y，输出变量为z。由前面的分析可知，OMP算法中会用到原子的范数，因此定义ρ(长度为n的向量)用于存放算法中经常使用原子的-范数，定义向量i用于存储已选定原子的索引。如图2所示为OMP算法在GPU上并行实现的流程图。

图2 OMP算法GPU并行化实现流程图

在OMP算法运行前，首先把矩阵AT和向量y中的数据从CPU内存传输至GPU的全局存储器;OMP算法执行结束后，将输出的z从GPU全局存储器中拷贝到CPU内存中。OMP算法的每一次迭代中都会用到ρ，为了避免频繁的重新计算，提前计算得到ρ并把它保存到GPU的全局存储器中。

OMP并行过程包含k次循环，每次循环求得一个原子的索引。在GPU上并行实现OMP算法方案如下:首先定义一个核函数，其中“·* ”表示两个向量的点乘。在这个核函数中，z用来区分原子是否已经被选中:如果z中相应原子不为零，则表示该原子已被选中，将在这个原子上的投影值设置为零，以避免该原子再次被选中。这种方法的优点是不需要额外的内存来区分原子是否被选中。其次，通过计算最大投影值来寻找最匹配原子的过程，使用CUBLAS库函数来实现。第三，采用矩阵逆更新算法和矩阵向量相乘块算法来实现矩阵求逆和矩阵向量相乘在GPU上的并行计算。第四，定义两个核函数，一个用于计算和的积，另一个用于更新残差r。

4 实验结果及分析

本实验是在Intel(R)core(TM)i7处理器12 Gbyte内存，NVIDIA GTX480显卡上完成的。实验的基本设置如下:传感矩阵Φ服从标准高斯分布;变换矩阵Ψ不影响算法的运行速度，因此令A=Φ。实验测试中，每组参数设置下的测量值都能够正确地恢复，选取以下6组实验数据进行比较分析，其中n和m分别表示传感矩阵Α的行和列，而k表示矩阵Α的稀疏度。

4．1 矩阵向量相乘

从表1的实验结果可以看出:基于GPU的并行矩阵向量相乘块算法相比其在CPU的串行算法运算速度提高了50多倍;且随着数据量的增加，加速效果更好，因而较好地解决了矩阵向量相乘计算耗时长的难题。

表1 矩阵向量相乘的结果对比

4．2 矩阵求逆

从表2的实验结果可看出:基于GPU并行矩阵求逆算法相比其在CPU上的串行算法运行速度提高了近2倍;其加速比只与稀疏度k相关，而不依赖于n和m的大小。即k相同时，并行求逆算法相比其串行算法加速比相同。

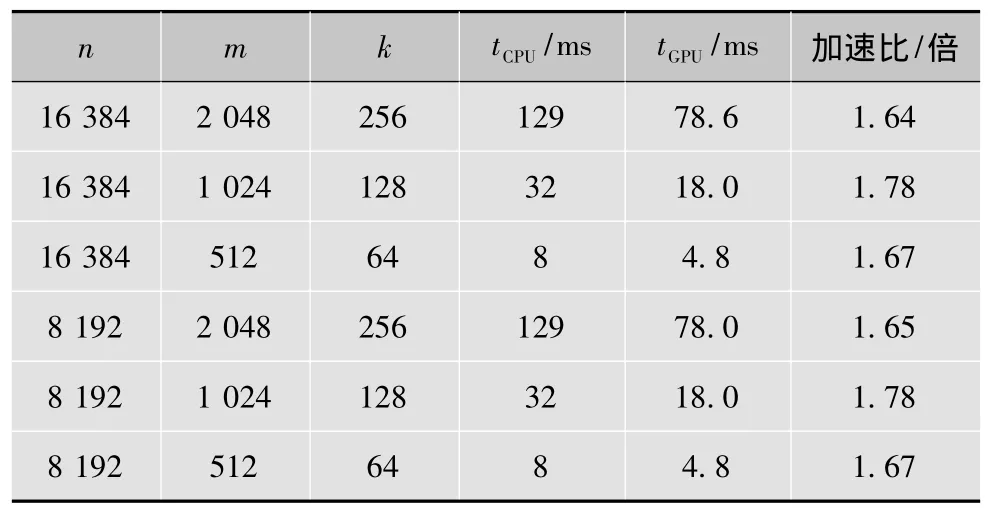
表2 矩阵求逆的结果对比

4．3 仿真结果

从表3的实验结果可以看出:基于GPU的并行OMP算法相比其CPU上的串行算法运行速度提高了30～44倍:当n=16 384时，加速比可以达到44倍;n=8 192时，加速比也可达到30多倍。实验结果充分地证明了基于GPU并行计算OMP算法的有效性和方案的可行性。图3是对表3中6组不同参数设置下并行OMP算法的加速效果图。

表3 仿真实验的结果对比

图3 并行OMP算法的加速效果

5 小结

本文在GPU平台上设计了一个并行OMP算法。通过分析OMP算法的复杂度发现，该算法的计算瓶颈在于矩阵求逆和投影部分的矩阵向量相乘。因此在矩阵求逆中使用矩阵逆更新算法从而大幅降低算法的计算复杂度，并在GPU平台上设计了矩阵求逆对应的并行算法;此外，利用分块思想设计了一个并行的矩阵向量相乘块算法以加速投影模型。实验结果表明，相比于串行算法而言，基于GPU的并行OMP算法可获得30～44倍的加速比，这充分说明了并行算法的有效性和方案的可行性。然而，通过对比表1和表3的实验结果可以发现，矩阵向量相乘计算所耗时间占总运行时间的2/3以上，也就是说，找到更好的矩阵向量相乘算法是提高OMP算法效率的关键。因此，对OMP算法中矩阵向量相乘的进一步优化，将是今后工作的重点。

［1］喻玲娟，谢晓春.压缩感知理论简介［J］.电视技术，2008，32(12):16-18.

［2］高睿.基于压缩传感的匹配追踪重建算法研究［D］.北京:北京交通大学，2009.

［3］ 方红，杨海蓉.贪婪算法与压缩感知理论［J］.自动化学报，2011，37(12):1413-1421.

［4］方红，章权兵，韦穗.改进的后退型最优正交匹配追踪图像重建方法［J］.华南理工大学学报:自然科学版，2008，36(8):23-27.

［5］ 吴凌华，张小川.贪婪算法与压缩感知理论［J］.电讯技术，2011，51(1):120-124.

［6］ TROPP J，GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Trans.Inform.Theory，2005，12(53):4655-4666.

［7］刘金硕，曾秋，邹斌，等.快速鲁棒特征算法的CUDA加速优化［J］.计算机科学，2014，41(4):24-27.

［8］张舒，褚艳利.GPU高性能运算之CUDA［M］.北京:中国水利水电出版社，2009.

［9］ FARBER R.CUDA application design and development［M］.San Francisco:Morgan Kaufmann，2011.

［10］ JASON S，EDWARD K.CUDA by Example［M］.Boston:Addison-Wesley，2010.

［11］ HAGER W W.Updating the Inverse of a Matrix［J］.SIAM Review，2008，31(2):221-239.

［12］ FUJIMOTO N.Faster matrix-vector multiplication on GeForce 8800GTX［C］//Proc.IEEE International Symposium on Parallel and Distributed Processing.［S.l.］:IEEE Press，2008:14-18.

［13］ FANG Yong，LIANG Chen，WU Jiaji，et al.GPU implementation of orthogonal matching pursuit for compressive sensing［C］//Proc.IEEE 17th International Conference on Parallel and Distributed Systems(ICPADS).［S.l.］:IEEE Press，2008:1044-1047.