LDO自激振荡故障的仿真建模方法研究
刘 淼(天津电子信息职业技术学院,天津 300350)
LDO自激振荡故障的仿真建模方法研究
刘淼
(天津电子信息职业技术学院,天津300350)
借助频域傅里叶分析的方法,对传统PMOS结构LDO系统的稳定性进行了仿真建模方法研究,阐述了引起环路不稳定的因素及其影响机制。结合一例LDO自激振荡故障的分析,指出故障发生的原因和相应的处理措施。
LDO;稳定性分析;失效模式;故障诊断
0 引言
低压差线性稳压器(Low-Dropout Linear Regulator,LDO)因其具有稳定性高、噪声低、功耗低、抗干扰能力强、响应快速等优点被广泛应用于计算机、网络设备、无线通信设备及芯片内部供电。因此LDO在一定程度上带动了很多产业的发展,具有相当广阔的发展前景。
环路稳定性作为重要指标,直接影响LDO在实际使用中能否正常工作。本文以PMOS结构LDO为例,进行小信号建模及瞬态响应分析,并以此为基础研究一例LDO输出电压自激振荡的故障,得出环路不稳定因素及其影响机制,给出解决的方法。
1 问题背景
某超高频RFID阅读器射频板,工作在UHF频段(840MHz~845MHz,920MHz~925MHz),基带信号接收频段为40kHz~640kHz,系统的低频噪声直接影响接收灵敏度指标。单板选用的低压差线性电压调整器是一款商用LDO,该LDO具有超低噪声(48μVRMS)和高PSRR值(在10kHz为49dB),因此被用于大负载电流的电压调整,为前接收链路供电。
单板调试过程中,发现LDO输出电压纹波异常(5.4V~5V的电平转换),Vpp达到1.6V,判断LDO处于正反馈自激振荡状态,测试结果如图1所示。
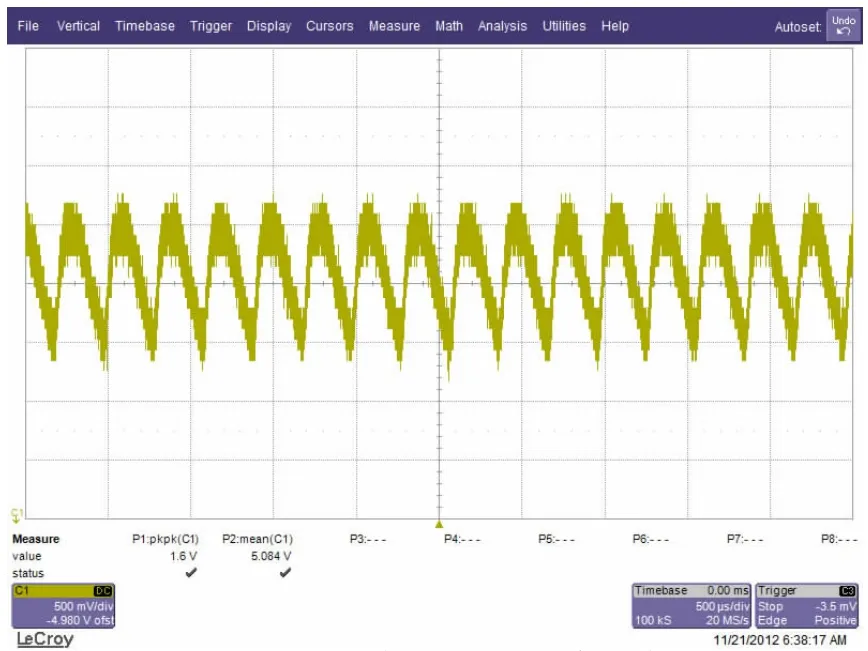
图1 LDO输出电压的异常纹波
LDO电路原理图如图2。其中C118和C16是输入端的去耦电容,C14和C117是输出端的去耦电容,R61和R34是反馈取样电阻,C106是反馈补偿电容,C15是NR|FB管脚的去耦电容。
2 小信号建模及瞬态响应分析
通过查看器件手册[1],LDO工作在输出电压可调模式。LDO原理框图如图3所示。当输出电压可调时,C15是反馈端的旁路电容。新引入的旁路电容与电阻R61形成一个RC滤波,造成反馈取样信号的延时,反馈端无法及时反映输出电平的情况,容易造成环路不稳定。从环路稳定性原理也可以得出,当LDO稳定工作时,旁路电容C15的引入会使C106产生的补偿极点频率减小,环路带宽减小,当新补偿极点的频率小于单位增益点时,其产生的负相移会大大增加,系统开环函数的相位裕度减小,容易造成环路不稳定,形成正反馈振荡。
下面将建立LDO的AC小信号模型[2],通过环路稳定性理论来分析故障的原因。
所用LDO是PMOS结构的LDO,如果不考虑过流、过温保护的情况,芯片正常工作时的等效模型如图4所示。LDO线性调整器可以分为4个基本的功能模块:调整管(Pass Element)、电压基准(Voltage Reference)、误差放大器(Error Amplifier)和电阻反馈网络(Feedback Network,包含电阻R1和R2)。误差放大器的小信号模型是跨导ga,电容Cpar和电阻Rpar是它的寄生输出阻抗,同时也是调整管的栅极输入阻抗。串联调整管(PMOS晶体三极管)的小信号模型是跨导gp。LDO的输出电容Co,它的等效串联电阻是RESR,Cb是后级各电压输入器件的高频去耦电容,Cb<<Co。
MOSFET共有G、D、S 3个脚,通过G、S间加控制信号可以改变D、S间的导通和截止。PMOS源漏区的掺杂类型是P型,所以PMOS的工作条件是在栅上相对于源极施加负电压,形成从源到漏的源漏电流,|Vgs|=Vsg的值越大,沟道的导通电阻越小,电流的数值越大。在LDO降压转换器中,PMOS调整管作为电压控制电流源(VCCS),电流I=|Vgs|*gp,其中gp是跨导,它提供稳定输出电压VO所需的负载电流IL。输出电压VO由R1和R2分压得到的反馈信号作为误差放大器(EA)的输入,与基准源Vref进行比较放大Verr=ga*(Vfb-Vref),EA输出调整PMOS管的栅极电压,驱动PMOS管输出稳定电流,从而得到稳定输出电压VO。由此可见,LDO的稳定性即是输出电压的稳定性,它是由负反馈网络决定的。环路的负反馈特性要求EA的两个输入电压相等,即把反馈信号固定在一个参考电平上,因此得到VO=Vref(1+R1/R2)。
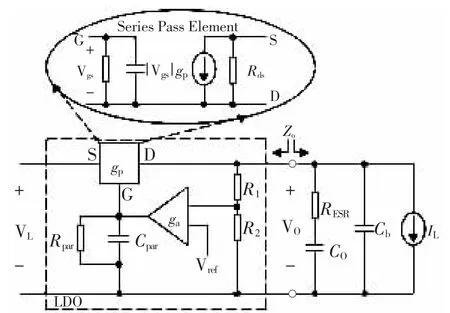
图4 LDO的AC小信号等效模型
模型中几个变量的常用取值[3]为:
(1)典型的误差放大器的直流增益为25dB~45dB。
(2)寄生电容Cpar一般取值为100pF~300pF。
(3)寄生电阻Rpar大约为300kΩ。
由LDO的小信号等效模型,得到输出阻抗为:
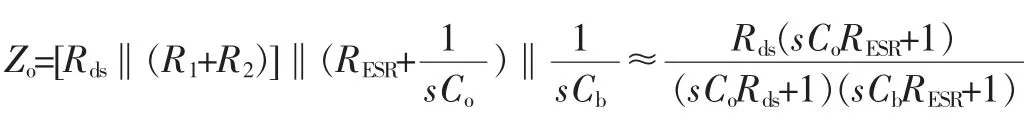
其中,Rds‖(R1+R2)≈Rds,Co>>Cb,Rds>>RESR。
前向通道传递函数为:
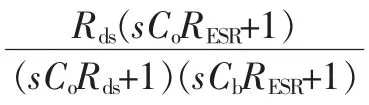
其中,Afw指前向通道增益,即PMOS管的增益,设置Afw=Gpmos=8=18.1dB(20log)。
反馈通道传递函数为:
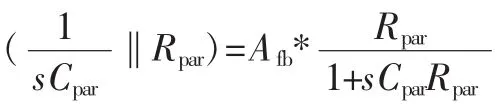
其中,Afb指反馈通道增益,包括反馈分压网络的增益和误差放大器的增益:
Afb=GEA*Gfb
GEA=35dB=56.2
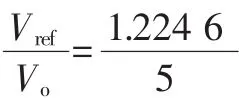
开环传递函数为:
G(s)=GfGp
化简G(s)可找出环路中的零点(Zero)和极点(Pole),主极点为:

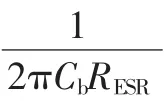
Pb与等效串联电阻RESR有关,当RESR很大时,Pb极点出现在低频,同样会减小相位裕度。
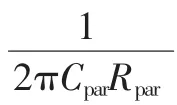
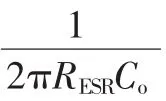
通常系统中存在3个极点(Po,Pa,Pb)和一个零点(ZESR),可以近似比较出4个零极点的大小:po<pa<ZESR<pb。
LDO所有输出电容相并联,总的ESR要满足的范围主要取决于大电容的小ESR值。通常认为,电容所含的寄生单元会降低其电性能,ESR是最重要的寄生单元之一。如果在设计时电容选择不恰当,将导致稳定性故障,并影响输出的时域瞬态响应[4]。图5为典型LDO的频率响应曲线。大多数LDO都要求其输出电容的ESR满足特定范围,以保证环路的稳定性,并根据ESR的稳定区间选取合适的电容类型:固体坦电解/铝电解/多层陶瓷电容。
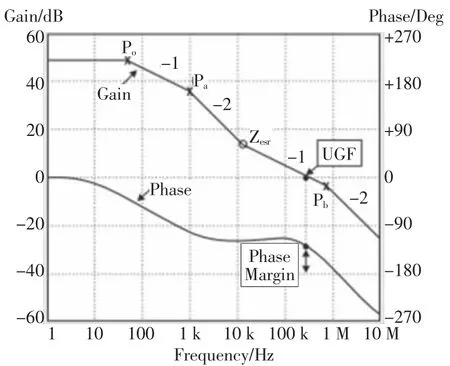
图5 典型LDO的频率响应曲线[2]
图6为LDO当输出电容为10μF时,不同负载电流所对应的ESR稳定范围曲线,作为电容选择时的参考,即规定了特定负载电流和特定输出容值条件下,其等效串联电阻RESR在工作温度范围内的阻值上限,超过上限会引起环路不稳定。
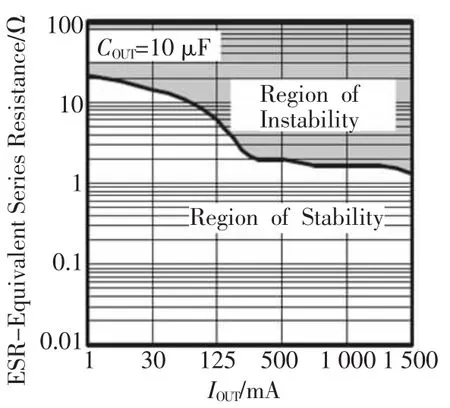
图6 LDO的稳定ESR范围[1]
从图6可以看出,随着负载电流的增大,ESR的取值上限在降低,这是因为随着Iout增大,主极点Po频率升高,主极点产生的负相移减小,因此零点(反比ESR)可以减少正相移的补偿,ZESR频率升高则ESR的取值上限可以相应减小。
环路的稳定性补偿除了使用输出电容的等效串联电阻RESR来获取有效的正相移之外,在大多数输出可调LDO稳压器中,都通过在取样电阻R1上并联补偿电容CFF来获得正相移[5]。
如图7所示,反馈网络由R1、R2和CFF组成,反馈网络的传输函数为:
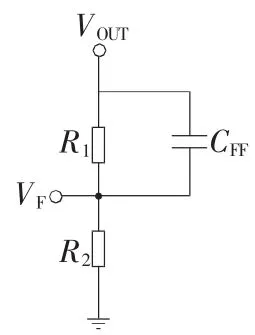
图7 电容电阻反馈网络A
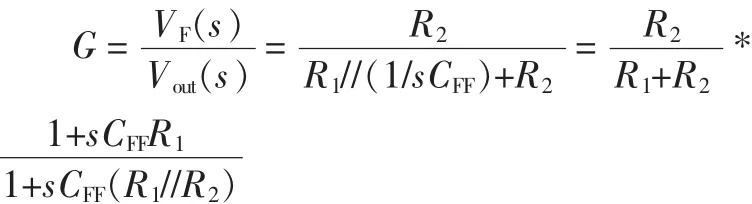
R1、R2和CFF形成一个极点/零点对,这里零点的频率总比极点的频率低,零极点频率由如下公式给出:
FZERO=1/(2×π×CFF×R1)
FPOLE=1/(2×π×CFF×(R1//R2))
如图8所示,与原理图对应,反馈网络由R1、R2和CF1、CF2组成,电容电阻反馈网络的传输函数为:
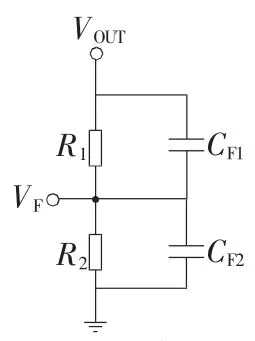
图8 电容电阻反馈网络B
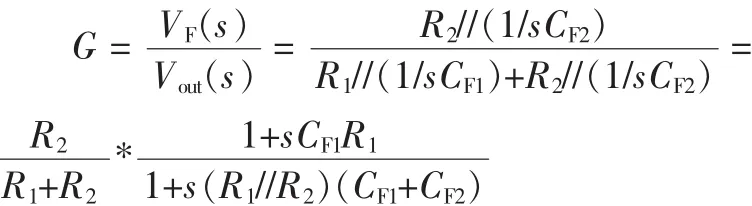
R1、R2和CF1、CF2形成一个新的零/极点对,零极点频率由以下公式给出:
FZERO=1/(2×π×CF1×R1)
FPOLE=1/(2×π×(CF1+CF2)×(R1//R2))
相比于反馈网络A产生的零极点对,反馈网络B产生的零点频率不变,极点频率减小,这就增加了系统的负相移,使单位增益点(0dB)频率对应的相位裕度减小,环路的不稳定性增大。
下面根据实际LDO系统设置具体参数,通过绘制bode图得到系统的相位裕度,从而证明,正是CF2取值不当使系统的相位裕度减小到不稳定区域,最终导致正反馈振荡。
系统开环传递函数为:
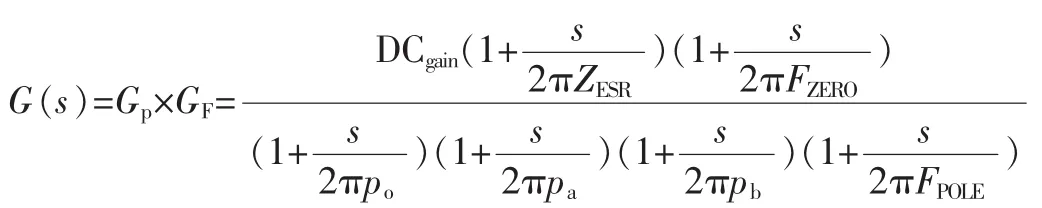
其中,直流增益DCgain=Gpmos×GEA×Gfb=8×56.2×(1.224 6/5)=110.12。
由原理图知,Co≈47μF,RESR=1Ω,R1=62kΩ,R2=20kΩ,CF1=20pF,CF2=0.1μF,Cb=56pF(SRF=900MHz),Cpar=200pF,Rpar=300kΩ,Rds=65Ω。
计算得到零极点的分布为:
Po=52Hz,Pa=2.65kHz,Pb=2.84GHz,ZESR=3.39kHz,FZERO=128kHz,FPOLE=526kHz(反馈网络A),FPOLE′=105Hz(反馈网络B)
由Simulink绘制出系统传递函数框图分别如图9和图10所示。
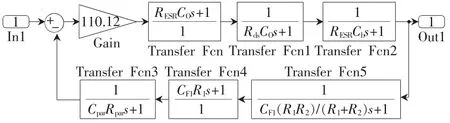
图9 系统传递函数框图(反馈网络A)
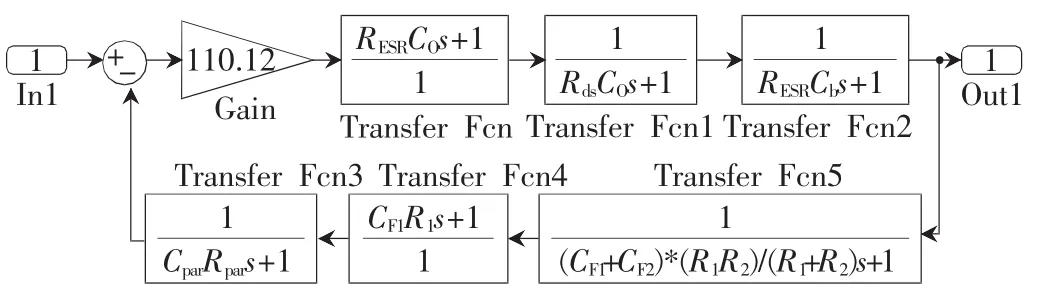
图10 系统传递函数框图(反馈网络B)
分别仿真得到它们的bode(波特)图如图11所示。
从图11可以看到,随着CF2的引入,补偿极点的频率明显减小(FPOLE→FPOLE′),回路带宽减小(4.81kHz→767Hz),补偿极点产生的负相移明显增大(-arctan(4.81k/526k)=-0.5°→-arctan(767/105)=-82°),相位裕度由86°减小到8.68°,负反馈环路处于不稳定状态,反馈信号与源信号相位相差很小,两信号相互叠加可能导致正反馈振荡。根据仿真结果,C15容值逐渐减小直到去掉的过程中,相位裕度逐渐增大(8.68°→86°),实测发现电压纹波逐渐减小,输出恢复稳定,与仿真结论一致。
3 结论
本文从理论上分析得到PMOS结构LDO的零极点分布,并仿真得到bode图,通过开环函数的相位裕度判断闭环系统的稳定性,结果表明补偿电容使用不当可能引起环路不稳定,导致自激振荡。根据仿真结果给出改进方案,实验与理论相符合。
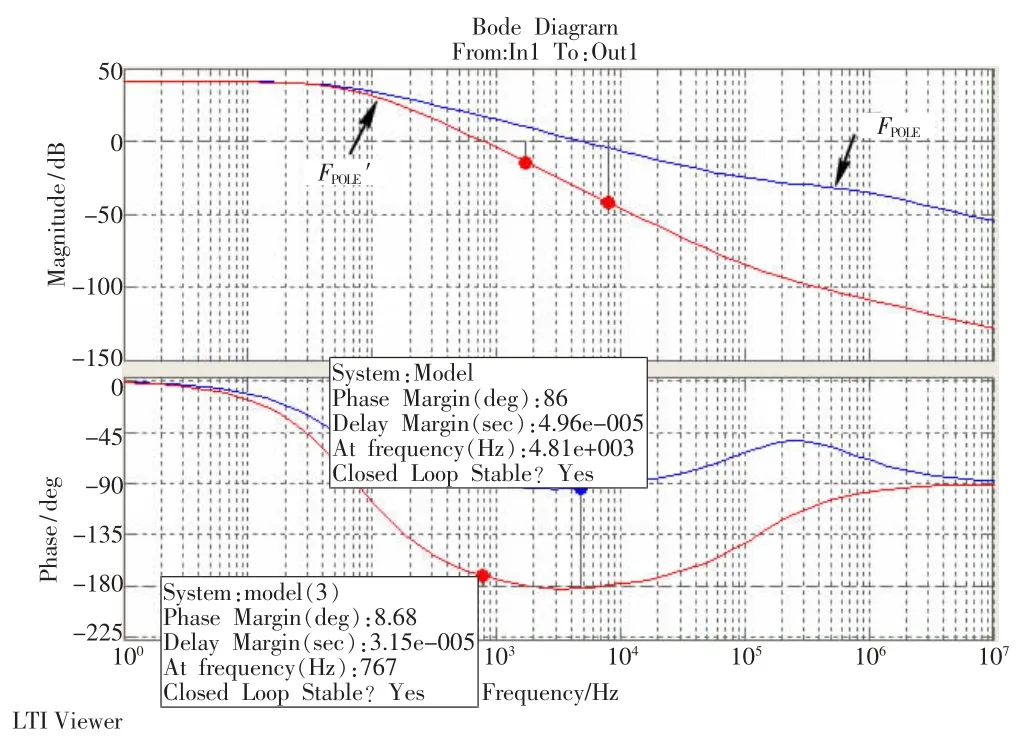
图11 波特图对比
[1]Texas Instruments Incorporated.Ultralow-noise,high-PSRR,fast,RF,1.5-A low-dropout linear regulators[EB/OL].[2014-06-08].http://www.ti.com.cn/cn/lit/ds/symlink/tps 78601.pdf
[2]LEE B S.Understanding the stable range of equivalent series resistance of an LDO regulator[EB/OL].[2014-06-08].http://www.ti.com.cn/cn/lit/an/slyt187/slyt187.pdf.
[3]Everett Rogers.Stability analysis of low-dropout linear regulators with a PMOS pass element[EB/OL].[2014-06-08].http://www.ti.com.cn/cn/lit/an/slyt194/slyt194.pdf.
[4]ALLEN G R,ADELL P C,Chen Dakai,et al.Singleevent transient testing of low dropout PNP series linear voltage regulators[J].IEEE Transactions on Nuclear Science,2012,59(6):2764-2771.
[5]SIMPSON C.LDO regulator stability using ceramic output capacitors[EB/OL].[2014-06-08].http://www.ti.com/lit/an/snva167a/snva167a.pdf.
Research on modeling methods of LDO self-excited oscillation fault simulation
Liu Miao
(Tianjin Electronic Information College,Tianjin 300350,China)
Using the method of Fouries analysis in frequency domain,this paper studied the stability of low dropout linear regulator with PMOS structure by modeling methods and illustrated the cause and influence mechanism of loop instability.An issue of ldo is taken for example,and the cause of issue and corresponding solution are investigated in paper.
LDO;stability analysis;fault modes;fault diagnosis
TN432
A
1674-7720(2015)10-0080-04
2014-12-31)
刘淼(1983-),通信作者,女,硕士,讲师,主要研究方向:射频电路设计与优化,可重构天线等。E-mail:fresh-1983@163.com。

