结构可靠度理论在公路桥梁设计中的若干应用研究

李继刚

(中国公路工程咨询集团有限公司,北京市 100097)

结构可靠度理论在公路桥梁设计中的若干应用研究

李继刚

(中国公路工程咨询集团有限公司,北京市 100097)

“定值设计法”长期在公路桥梁结构设计中被使用,但因为“概率极限状态设计法”的优越性能越来越凸显而逐渐将其取代。就结构可靠度理论应用于公路桥梁设计中的问题进行研究,重点研究桥梁结构可靠度的Monte—Carl0法(混凝土结构可靠度的Mc模拟)和实用分析方法,并研究工程界广泛使用的一次二阶矩法,针对其弱点,根据结构可靠度指标的几何意义以Jc法为基础,利用计算机建立结构可靠度指标计算优化模型,对求解方法着重研究,通过在桥梁工程中的实际算例证实这一方法切实可行并具有极高的优越性。

桥梁设计；结构可靠度；结构抗力：荷载作用；优化设计方法

0 引言

桥梁结构设计既要求能适用承载力及各项预定的功能要求,又要求能保障安全,同时能控制工程造价在合理范围,这是其要遵循的根本原则。可靠度和安全度分别用于度量可靠性和安全性,而桥梁的安全性并不同于可靠性,后者内涵外延更广。一座结构可靠性高的桥梁应该是安全的,能满足预定功能且经久耐用的。结构的安全性是在桥梁结构静止状态下及动态瞬间状态下结构可靠性的研究重点。结构的耐久性是在车辆反复荷载通行的情况下研究的重点。计算分析是建立在统计学基础上的,利用蒙特卡罗方法建立概率模型得到近似值来确定结构可靠度预定功能的概率,从而定量描述结构的可靠性。

1 结构可靠度基本理论

1.1 结构可靠度的基本概念

在规定的时间和规定的条件下,桥梁结构体的耐久性实际完成的功能与设计时预期要求完成的功能的概率,就是国际上对结构可靠度得到多数人认同的定义。

规定的时间指的是结合结构使用期对各种基本变量与时间的关系对结构可靠度进行分析所获得的基准时间。不考虑因为人的不当操作对结构产生影响因素,只考虑结构正常设计施工和使用的条件称为规定的条件。结构在施工和使用常态下能持续发挥各种应有作用、在正常使用时各方面性能保持正常,在正常维护下能够确保经久耐用,在突发事件发生过程中保持整体稳定性不被破坏,这四方面功能统称为预定功能。

“极限状态”被用为是否完成预定功能的衡量标志,也是结构工作状态是可靠或者失效的区分标志［1］。极限状态是指当结构设计规定的某一功能在结构整体或部分超出特定状态时不能得以满足的状态。在设计时应当要求对结构可能出现的各种极限状态的标志与极限值进行明确规定。承载能力极限状态、正常使用极限状态和“破坏—安全”极限状态三种极限状态是结构设计时通常要考虑到的极限状态。承载能力极限状态是指桥梁结构的最大承载能力,当通行荷载超过这个极限时结构将出现变形,进而影响结构的安全。所以,为了保障安全,工程在设计时要求对承载能力极限状态进行设计,并将失效概率控制在极低的水平。当结构整体或部分失去平衡,如错位、倾覆或者本身材料遭到过度破坏产生很大程度的变形而不能再行承载、结构本身体系转为机动或者出现压屈等情况使结构或构件丧失稳定,这四种情况通常被认为承载能力超过极限状态。

1.2 正常使用极限状态

公路桥梁结构或其构件符合正常使用并具备耐久性能时,所对应的工作条件和耐久程度即为正常使用极限状态。当公路桥梁结构出现外观变形、耐久性能局部破坏、正常使用时出现振动或其它特定状态等使桥梁不能正常使用时,即为异常使用极限状态。

1.3 “破坏-安全”极限状态

超过极限状态使结构体局部发生破坏而其余未被破坏的部分仍能继续发挥承载作用但承载要求可以降低,结构体本身仍有一定的可靠度而非完全丧失功能,这种状态即“破坏—安全”极限状态,又称条件极限状态［2］。结构在偶尔事件发生后只要求结构体本身没有酿成巨大损失即可,而不要求结构保持完全不受损的程度,这种理论常用于桥梁抗震和连拱推力墩的计算等方面的指导。

2 公路桥梁荷载作用和结构抗力的分布及统计参数研究

2.1 结构可靠度分析的蒙特卡罗方法

在数学或者物理学领域,人们会采用统计抽样理论来计算出无限接近正确答案的近似答案,这种计算方法即为蒙特卡罗方法。首先,根据问题建立相似的概率模型,利用这种相似性的一些概率模型的特性和数学计算与你的解答联系在一起,然后利用模型随机模拟、统计抽样,其结果对这些统计特征的统计估计值作为原始数学问题近似值,这就是利用蒙特卡罗方法解决问题的基本思想。足以见得失效概率即桥梁结构失效次数与抽样总数比率就是蒙特卡罗法的基本点。有直接法、平均值法、半解析法以及改进法等都被蒙特卡罗法用作计算失效概率的方法。其中,直接法是直接的数值模拟的极限状态方程的随机变量,以得到结构的失效概率,即结构失效频率、采样频率和M的比率［3］。失效频率随着抽样次数的增多不断接近于失效概率。

只有满足概率分布函数F或概率密度函数,才能得到所需要的各随机变量x,这是解决问题的关键。根据随机变量函数的理论,通过变换或者计算生成其它任意分布的随机变量,这种情况只需具备有连续分布的随机变量即可。随机变量的最佳选择是区间均匀分布的随机变量,因为它最简单最基本。由于随机数列点在区间上分布均匀,通过数学变换的方式就能得到其它分布的随机数列。这种电子计算机是有效的,可直接用于均匀分布的随机数函数或程序,如RAND等。在一般通过使用剩余的数值转换获得法,随机数生成,严格来说不是随机的,因此它被称为伪随机数。但是,如果计算方法好,它们类似于独立和均匀分布。

蒙特卡罗方法的可靠性研究的主要优点是：它避免在结构可靠性分析的数学难度,不考虑极限状态表面的复杂性,该变量和极限状态方程的分布简洁,容易计算约束［4］。

蒙特卡罗方法的可靠性研究的主要缺点在于：

(1)数据序列在大多数情况下是不能产生真正的随机数的,基于有这种可能性的数据统计所得到的结果并不会完全准确;许多随机数存在群聚效应使得观测得到的值没有实际意义而不被采用,造成浪费,进而使模拟效率下降；

(2)必须根据特定的随机过程和史料,否则直接影响计算结果的准确性；

(3)研究人员只有具备相应的统计学有关知识，才能用模拟方法构造模型和进行分析,因此只有时间充足、经验丰富的研究人员才能胜任这个工作；

(4)模型质量直接影响到检测结果的准确性,因此对模型质量要求高,且要明确模型自身存在风险。

(5)计算量大、计算时间长。

2.2 蒙特卡罗方法的求解步骤

蒙特卡罗方法的解题步骤如下：

(1)根据问题的需要构建一个简单的应用程序概率模型或随机模型,使问题的答案相对应于随机变量在模型中的特征(如概率、均值和方差),模型能与主体的实际问题或系统特征参数保持相同。

(2)根据每个随机变量在模型中的分布,以在计算机上产生随机数,实现足够随机数量的处理,完成“抽样”。平时第一步先生成均匀随机数,然后生成满足某一分布条件的随机数,随机模拟试验才能进行。

(3)根据随机变量的分布特征和概率模型的特征,设计和选择适当的抽样方法,每个随机变量进行抽样(包括直接取样、分层抽样、相关抽样、重要抽样)。

(4)问题的随机答案依据模型通过仿真实验和计算来求出。

(5)通过统计的测试结果的分析,得出概率解和解精度估计。在可靠性分析与设计中,采用蒙特卡罗模拟方法不仅能确定复杂的随机变量的概率分布和特征,而且还可以模拟随机过程、优化系统参数等。

2.3 蒙特卡罗方法时要注意的问题

注意以下4点有助于提高在实际应用蒙特卡罗技术解决实际问题的有效性。

(1)开发一套系统性强的抽样方法用于数值抽样；

(2)选择的模拟技术或者抽样策略要经济可靠,并且适合于要测算的样本；

(3)认真对待计算功能函数的复杂程度,选择足够多的数据作为模拟技术基本变量,从而提高计算结果的准确性。

(4)一个合理的估算应该能够从给定的模拟技术来得到其所需要的抽样数量。

2.4 公路桥梁荷载作用和结构抗力的分布及统计参数研究

这里提到的公路桥梁荷载作用指的是公路桥梁恒载,由构件重和桥面重组成的钢筋混凝土和预应力混凝土桥式梁的上部结构自重。桥面铺设的装修材料自身重量和桥梁的梁或板本身的重量不能混为一体,应分开测定,最后再组合成上部结构的自重。恒载因不随时间的变化而产生较大变化被认为在设计期间内其量值保持恒定,属于永久荷载,可用机变量概率模型进行描述,并可认为服从正态分布。分布参数见表1

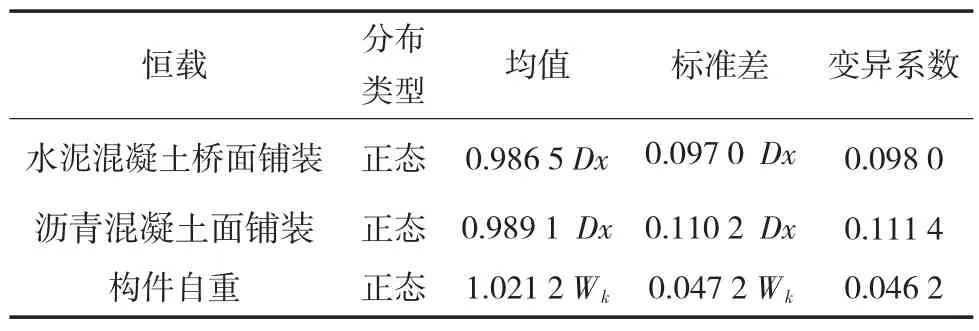
表1 桥面铺装层自重及构件自重的统计分析

恒载的统计参数(其服从正态分布)可在求得沥青混凝土桥面铺装层和构件自重统计参数的基础上进行进一步分析得到。窗体顶端车辆活荷载是桥结构的基本可变负荷,占有负荷的各种组合的重要地位,因为其随时间变化,车辆活荷载的重要位置应该由随机过程模型进行说明。车辆荷载中车重或轴重、车间距、轴距等参数会对桥梁结构中的效应产生影响,为了控制各种参数的影响,可对大量各种不一样的桥型及跨径进行计算求得各种类型的荷载效应,而不是采用难度较大的直接引入桥梁可靠度分析的方法。

结合我国当下执行的车辆荷载标准及其现状对实际测得的交通数据进行分析,把车辆运行状态分为一般运行和密集运行两种状态。对要测试的目标桥梁在规定时间内进行实地统计,获得该桥梁不同时间段内通行车辆的类型、车身及货物重、车子的总长度、行驶的速度、车辆间隔距离等变化关系,统计分析荷载幅值(总重或轴重)、时点变化过程,得到任意时点荷载幅值的分布、随机过程类型,并推算求出设计基准期内最大值分布,以确定车辆活荷载随机过程的类型和统计参数。

3 结语

“定值设计法”长期在公路桥梁结构设计中被使用,但因为“概率极限状态设计法”的优越性能越来越凸显而逐渐将其取代。利用数学统计的手段,通过度量结构的可靠性来确定结构的失效概率,并将其应用于公路桥梁结构设计中。将结构可靠性理论应用于工程结构计算实践中,并针对其中一个非常重要的问题进行研究,即研究能方便、精确地计算结构可靠指标或失效概率的方法。本文通过对几种得到广泛应用的实用计算方法进行讨论,针对其弱点提出新的优化方法,并用工程实例说明其优越性和适用性。

［1］ 赵国藩,贡金鑫,赵尚传.我国土木工程结构可靠性研究的一些进展［J］.大连理工大学学报,2012(3)：254.

［2］ 张建仁,刘扬,许福友,等.结构可靠度理论及其在桥梁工程中的应用［M］. 北京：人民交通出版社,2002.

［3］ 张建仁,张起森.公路工程结构可靠度理论及其应用［M］. 北京：人民交通出版社,2005.

［4］ 李扬海,鲍卫刚,郭修武,等.公路桥梁结构可靠度与概率极限状态设计［M］.北京：人民交通出版社,2013.

U441

A

1009-7716(2015)09-0202-03

2015-04-20

李继刚(1981-)，男,江西南昌人,工程师,从事公路桥梁设计工作。