机械设备集群大数据系统研究与应用
沈阳鼓风机集团股份有限公司 张建茹 郭庆丰 闫强
华电福新能源股份有限公司甘肃分公司 李乐 赵礼永
机械设备集群大数据系统研究与应用
沈阳鼓风机集团股份有限公司 张建茹 郭庆丰 闫强
华电福新能源股份有限公司甘肃分公司 李乐 赵礼永
对设备进行连续的数据采集与储存的基础上,获得反映设备状态的数据,系统通过对获得的大数据进行处理以及研究,从而对设备的健康状态进行一个合理的评估。为了有效地监测机组异常变化以及进行机组状态评估,必须选取合理的特征参量,并对这些参量进行监控。通过结合自动设置报警门限以及与特征参量门限值相关联的报警策略,实现了系统对机组的运行状态监测、异常识别、状态评估,甚至是故障部位识别,建立智能诊断系统。
大数据采集与存储 状态监测 数据分析 故障诊断 门限值。
1 大数据存储
传统关系型数据库已不能满足互联网应用需求的情况下,开始出现一些针对结构化、半结构化甚至非结构化数据的管理系统。在这些系统中,数据通常采用多副本的方式进行存储,保证系统的可用性和并发性;采用较弱的一致性模型(如最终一致性模型),在保证低延时的用户相应的同时,维持复本之间的一致状态;并且都提供良好的负载平衡策略和容错手段。
按照数据管理方式划分,集中式数据管理系统和非集中式数据管理系统两大类。
2 大数据处理
在信息时代,互联网已经成为了世界范围内最大的数据仓库。如何快速地从这些海量数据中抽取出关键的信息用以提高互联网应用的质量、用户体验等,已经成为了互联网企业之间竞争的关键技术问题。同时,大规模数据处理的研究,也是DISC应用研究的关键问题。
解决大规模数据处理的方法就是并行计算。将大量数据分散到多个节点上,将计算并行化,利用多机的计算资源,从而加快数据处理的速度。目前,这种并行计算主要分为三大类,一类是广泛应用于高性能计算的MPI(Message Passing Interface,消息传递接口)技术,一类是以Google/Yahoo为代表的互联网企业兴起的Map(映射)/Reduce(化简)计算,一类是微软提出的Dryad并行计算模型。
3 机械设备运行工况智能识别技术
现行大数据有结构化、半结构化与非结构化之分,对于结构化大数据(大规模样本+高维变量),研究了大数据分类分析方法,主要包括:支持向量分位数回归、神经网络分位数回归、L1 Logit回归、大规模数据分位数回归等。这些大数据分类分析方法,能够准确地识别机械设备运行工况,具体过程如下:
第一,收集所监测机械设备历年来的运行工况参数,基于对其工况特点的统计分析,给出对其工况的合理分段(确定工况类别数);
第二,根据正常工况下机械设备的功率、针对幅值等信号,将每一组工况参数分到不同的类中,形成带有类别标签的样本集;
第三,利用这些样本训练支持向量分位数回归、神经网络分位数回归、L1 Logit回归、大规模数据分位数回归等,得到相应的模型(估计出模型参数);
第四,将此模型应用到机械设备,则可以通过输入当前的工况参数到此模型,模型会自动给出当前工况的类别。
4 神经网络分位数回归模型的应用
现实中,解释变量和响应变量之间的关系模式不一定是线性的,非线性关系即使存在,其函数形式也很难准确确定,主要表现为:非线性函数fx1(X1)的形式很难选择和设计。常见的做法是将非线性函数进行线性近似:局部多项式展开或B-样条基函数展开,使用线性分位数回归方法逼近非线性分位数回归结果,局部多项式分位数回归与B-样条分位数回归就是其中的典型代表。或者可以使用非参数方法解决非线性函数误设问题,即建立非参数分位数回归模型。
神经网络分位数回归(QRNN)由Taylor首次提出,是一种灵活的非参数的分位数回归建模方法。分位数回归神经网络将分位数回归和神经网络的优点相结合,表现出强大的功能:一方面,通过分位数回归方法可以揭示解释变量对响应变量整个条件分布的影响;另一方面,通过神经网络结构可以模拟解释变量对响应变量的非线性影响模式。
因此,由前文介绍,进一步考虑神经网络的分位数回归问题,我们就可以得到神经网络分位数回归(QRNN)模型
式(29)
式中,权重向量W(ζ)与阈值向量b(ζ)都依赖于分位点ζ的变化。特别地,当隐层转换函数g(h)j和输出层转换函数g(o)都是等值函数时,QRNN模型就退化为线性分位数回归模型。
在QRNN模型中,隐层节点的数目n决定了模型的复杂程度,Taylor(2000)给出其选择准则,可以采用K折交叉验证法得到隐含层结点数目。K折交叉验证法的基本思想是:将原始训练划分成两个部分,训练集与验证集;将数据集分成大小相等的子集K份,每个子集分别作一次验证集,其余K份子集作为训练集,因此,在一次K折交叉验证法中,相对应要建立K个模型,并且对这K个模型的验证结果计算平均辨识率。理论上,K要足够大,才能使得训练集样本数足够多,实践中,K=10已经足够大。文中选择K=5进行交叉验证。
前文已经定义过非对称损失函数Pl(u),但是,该函数不是处处可微,它在原点处的倒数没有定义。因此,我们可以考虑用一个处处可微的函数逼近代替。根据Chen(2007)在分位数回归方法中使用的Huber(1981)准则,可以构建平滑算法逼近非对称损失函数Pl(u)。
Huber准则h( u)是 L1(绝对误差)准则和 L2(平方误差)准则的混合使用, L1准则用于描述绝对值误差项大于给定阈值ε的值,L2准则用于描述绝对值误差项小于给定阈值ε的值:
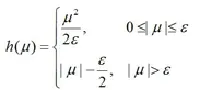
这个方程准则提供了绝对误差和平方误差在原点处的平稳过渡。Huber准则可以被用来逼近损失函数,新的逼近损失函数为
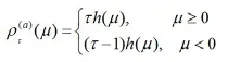
因此,此时标准的基于梯度的优化算法可以被用于优化模型参数。即QRNN模型的参数向量可以使用逼近损失函数
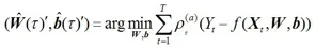
此外,为防止神经网络出现过度拟合现象,可以对QRNN模型的误差项增加一个二次惩罚项,因此可有
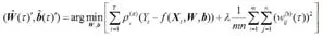
估计得到。其中,λ为惩罚参数。
5 基于大数据分析的机械设备异常状态智能报警方法
1)基本观点与思想
振动信号是设备运行状态的体现,正常的设备其振动信号应该服从某一特定的正态分布。当设备产生异常,其振信号必将产生偏移,可以划分为三种情况:第一,位置偏移,仍然服从正态分布;第二,位置不变,方差变大并且不服从正态分布;第三,位置偏移且不服从正态分布。为此,可以使用统计过程控制的基本方法与原理,对振动信号进行系统分析,判定其变动模式,进而推断设备异常情况,给出智能报警机制。
2)EVMA控制图
EWMA控制图采用指数加权移动均值设置控制线,因而可以不受正态假定的限定、加之图上的每个点包含着前面所有子组的信息,具有检验出过程均值小漂移的敏感性。
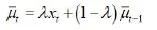
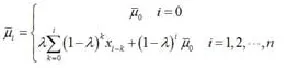
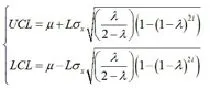
当t无穷大时,为
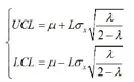
接下来考虑EWMA统计量的平均运行长度ARL
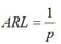
其中,p为第一个点落在控制限外的概率。根据3□原则,p=0.0027,则ARL=370。然后根君3□原则,使受控ARL=370,选择参数。
3)自适应门限法
自适应门限算法是当连续超过门限值的时间区间的个数超过一定的设定时就报警的检测算法。为了应对观测值周期性变动和长期趋势,门限值以观测值的均值为基础进行自动调整。假设是相互独立的观测值序列,。xt是第t个时间区间(设备采样区间)上的观测值。将□t□1设定为门限值,考虑一个向上的幅度,设置报警条件为
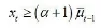
式(10)
其中,□t□1是前t□1个时间区间上序列均值的估计,可以通过式(51)计算得到,门限值□t□1能够随着t的变化进行自动的调整。
直接运用上述算法会产生较高的误报率,简单的改进会改善上述算法的性能。设定一个值k,当连续超过门限值的时间区间的个数大于或等于k时就报警,即
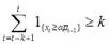
式(11)
其中,1k>。
上述算法的调整参数包括幅度参数□、EWMA的参数□、连续超过门限值的时间区间的个数k。
4)CUSUM方法
CUSUM算法是依赖于假设检验的异常点检测算法,目的是当异常点出现后尽快将它检测出来。对该问题的精确统计描述如下:对某个正整数v,观测值yyLy为独立同分布变量,其共同分布为,而观测值则是来自F1(y)的独立同分布变量,。显然,若v=n,则说明没有异常点,所有观测值均为独立同分布变量。另一方面,若有异常点v<n,那检测方法应尽快发现异常点,并报警。
[1]贺兴书.机械振动学[M].上海:上海交通大学出版社.1985.[2]郑水英.设备故障诊断[M].北京:化学工业出版社.2006.
[3] 沈庆根.化工机械故障诊断技术[M].杭州:浙江大学出版社.2006.
[4]刘文艺.风力发电机振动检测与故障诊断研究[D].重庆:重庆大学.2010.
[8]陈安华.旋转机械若干非线性故障现象的分析与研究[D].长沙:中南工业大学.1997.
[9]米勒P C.席伦W O,著.线性振动[M].曾子平.向豪英,等译.天津:天津大学出版社.1989.
[10]黄文振.多跨转子-轴承系统振动稳定性试验研究.机械工程学报.1995.31(5):34-38.
[11]钟掘.机械非线性故障现象的描述.诊断与预测[J].世界科技研究与发展.1996.18(6):15-19.

