复用技术耦合率失真优化的多图像加密机制

陈 阳，郑涵容

(1.浙江传媒学院 教育技术中心，浙江 杭州 310014；2.浙江艺术职业学院，浙江 杭州 310014)

复用技术耦合率失真优化的多图像加密机制

陈 阳1，郑涵容2

(1.浙江传媒学院 教育技术中心，浙江 杭州 310014；2.浙江艺术职业学院，浙江 杭州 310014)

为了解决当前多图像加密机制存在串扰效应以及失真现象等难题，提出了复用技术耦合率失真控制优化的多图像并行加密机制。基于DCT(Discrete Cosine Transform)变换与ZigZag扫描，设计复用技术，将多个明文压缩成一个复合置乱图像；并引入结构相似度，设计率失真控制优化技术，嵌入到复用技术中，优化失真值，减少失真度；再利用2D Arnold混沌映射对复合置乱图像进行二次置乱；再结合混沌相位掩码，构造双重加密函数，对置乱图像进行扩散。仿真实验结果表明：该加密机制高度安全，具备优异的加密质量与强烈的密钥敏感性能；且与当前多图像加密机制相比，该算法的解密质量更加优异，更能降低串扰效应。

多图像并行加密；复用技术；率失真控制；混沌掩码；串扰效应

随着网络信息和计算机科学的蓬勃发展，网络交流已经成为人们日常沟通不可缺少的一种方式，给生活带来了很大的便利[1]。但由于免费外放的网络环境，对传输文件信息的安全带来了严重威胁，特别是图像，因其所涉及到信息非常多，包括国防机密、商业机密等，防止图像信息被窃取已经成为研究人员的焦点。加密技术作为一种有效的方式，能够有效防止数字图像在传输过程被肆意攻击篡改[3]，但是这些算法忽略了图像的本质特性，不适合用于图像加密。对此，诸多学者提出了一系列适用于图像的加密算法。如Zhang G[4]等人设计了基于混沌映射的快速图像加密算法，通过迭代Tent映射，产生一个密钥流和一个与明文图像大小相同的P盒子，共同置乱图像，再对置乱图像进行加密，并测试其算法的加密性能，数据表明其算法高度安全。Mao[5]等人对三维混沌CAT映射进行改进，利用改进的混沌映射产生混沌序列设计了具有实时安全匀称加密机制，并对其算法进行了仿真验证，仿真结果表明该算法具有较好的加密效果，密钥空间巨大，增强了加密系统的抗攻击性能。Abdullah[6]等人引入遗传算法，提出了基于DNA算法与混沌理论的图像加密优化算法，对密文进行优化，并测试了该算法的加密性能，结果显示该算法高度安全，具备优化功能。尽管上述图像加密算法具有较高的安全性，能够有效保护图像信息被肆意篡改与窃取，但是这些算法只能对单个图像进行加密，无法对多图像同步加密。

为此，学者们相继开发了一些多图像加密算法。如张文全[7]等人设计了一种基于非对称密码系统的多图像加密算法，引入幅相调制技术与相位截断运算，通过光学系统，将5幅图像加密成1个密文，并测试了其算法的合理性与加密性能，实验结果显示其算法具有较好的加密质量与安全性。郭雨等人[8]等人引入复用技术和NTICE算法，提出了基于NTICE算法的图像同步压缩加密机制，并对其算法进行了测试，实验结果表明其算法能够对多个图像进行加密，且算法高度安全，具有较快的运行效率。龚黎华[9]等人设计了频谱切割融合Arnold变换的彩色图像加密算法，基于频谱切割技术，将单一彩色图像的三个分量复合成一个混合频谱，再利用Arnold变换与相位掩码对混合频谱加密，实验结果显示其算法具有良好的加密效果。

尽管当前的多图像机制能够对多幅图进行同步加密，且算法高度安全，但是这些算法在对多图像进行压缩时，失真值较大，且存在串扰效应，导致解密质量不佳。

为了解决上述问题，实现对多个图像进行并行加密，并有效消除串扰效应和失真现象，本文设计复用技术，将多个明文压缩成一幅复合置乱图像；引入结构相似度，设计率失真控制机制，嵌入到复用技术过程，控制图像压缩；再利用2D Logistic映射对复合置乱图像进行二次置乱；结合混沌掩码，构造双重加密函数，对二次置乱图像进行扩散。最后借助MATLAB仿真测试，通过对比技术测试本文机制。

1 复用技术

对n个初始明文执行并行加密，首先需将其压缩成1幅复合图像。故本文引入DCT(Discrete Cosine Transform)变换与ZigZag技术，设计复用技术来同步完成图像的压缩与初始置乱，获取复合置乱图像。其复用机制见图1。

图1 本文复用技术的示意图

具体步骤如下：

1)图像经DCT(Discrete Cosine Transform)处理后，其信号能量主要位于DCT系数中的直流与交流分量。故本文对每个明文进行j×j分块，利用DCT函数，将明文图像转换成DCT系数矩阵A1,A2,A3…An。DCT模型为

(1)

式中：F(u,v)代表变换系数矩阵；x,y代表2D图像f(x,y)的数据坐标值；M×N代表明文尺寸；u,v代表F(u,v)的数据坐标值；cos(A)代表余弦变换；K(u),K(v)均为常数

(2)

(3)

1个2D图像，经8×8分块后，利用上述DCT处理后，可以用DCT变换域中的8×8系数表征。例如，以2D灰度图像转为例(见图2)；经过DCT模型处理后，可获取8×8的系数矩阵，即

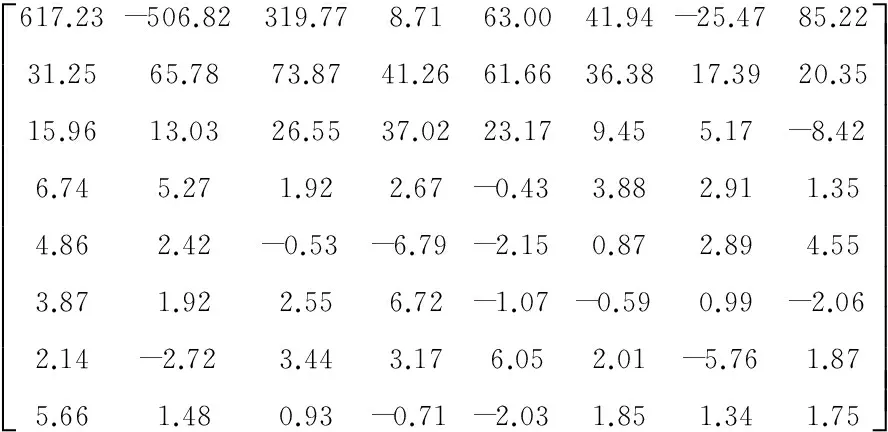
图2 2D明文灰度图像

2)为了提高算法安全性，本文引入ZigZag技术，对DCT系数矩阵A1,A2,A3,…,An进行扫描，按照扫描轨迹形成1D数组 a1,a2,a3,…,an。ZigZag扫描见图3。

3)将步骤2)中得到数组a1,a2,a3,…,an按照行(列)转换，形成1个2D复合矩阵B=(b1,b2,b3,…,bn),有

bi=ai

(4)

4)再利用IDCT(InverseDiscreteCosineTransform)函数，将B=(b1,b2,b3,…,bn)转变成一个复合图像，完成多图像压缩

图3 ZigZag扫描示意图

(5)

2 率失真控制优化设计

虽然复用技术能够将多幅明文压缩成一幅复合图像，但是在压缩中其编码率不能有效控制与优化，产生了较大幅度的失真，导致解密密文质量不佳。故本文引入结构相似度[10-11]，并基于拉格朗日拟合技术，设计率失真优化机制，控制图像压缩。率失真控制优化流程图见图4。

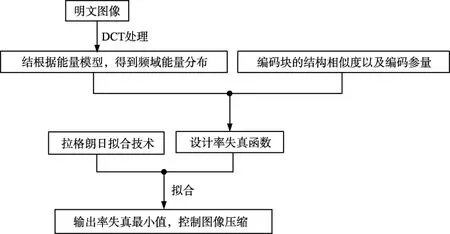
图4 率失真值优化示意图

根据上文可知，经过DTC处理后，图像从空域演变成系数矩阵(如表1)，得到图像的能量信号。能量分布模型如下

(6)

引入结构相似度SSIM(x,y)，利用SSIM(x,y)来求解图像失值；并联合能量分布以及编码参量，设计率失真控制函数φ；并利用拉格朗日技术对φ进行拟合，输出最小的φ。率失真控制函数φ模型如下[10-13]

(7)

(8)

(9)

(10)

失真D(η)模型如下[11]

(11)

式中：DiffS(x,y)代表明文与解密图像在坐标(x,y)像素能量差演变为频域的系数；H代表哈德曼矩阵

(12)

整个编码过程采用常规的方法，本文不做介绍。

在MPEG-4编码器中，利用率失真控制优化技术以及文献[8]、文献[9]中的技术对图1进行压缩编码，测试明文与解密图像之间的信噪比PSNR，得到了率失真曲线图，见图5。从图5中可知，相对于其他两种技术而言，本文引入率失真控制优化技术后，其PSNR值最大，这显示了明文与解密图像很接近，大幅减小了失真度；而文献[9]的失真程度最为严重，PSNR值最小，原因是单一的频谱切割机制存在数据丢失，切掉了高频直流分量部分。

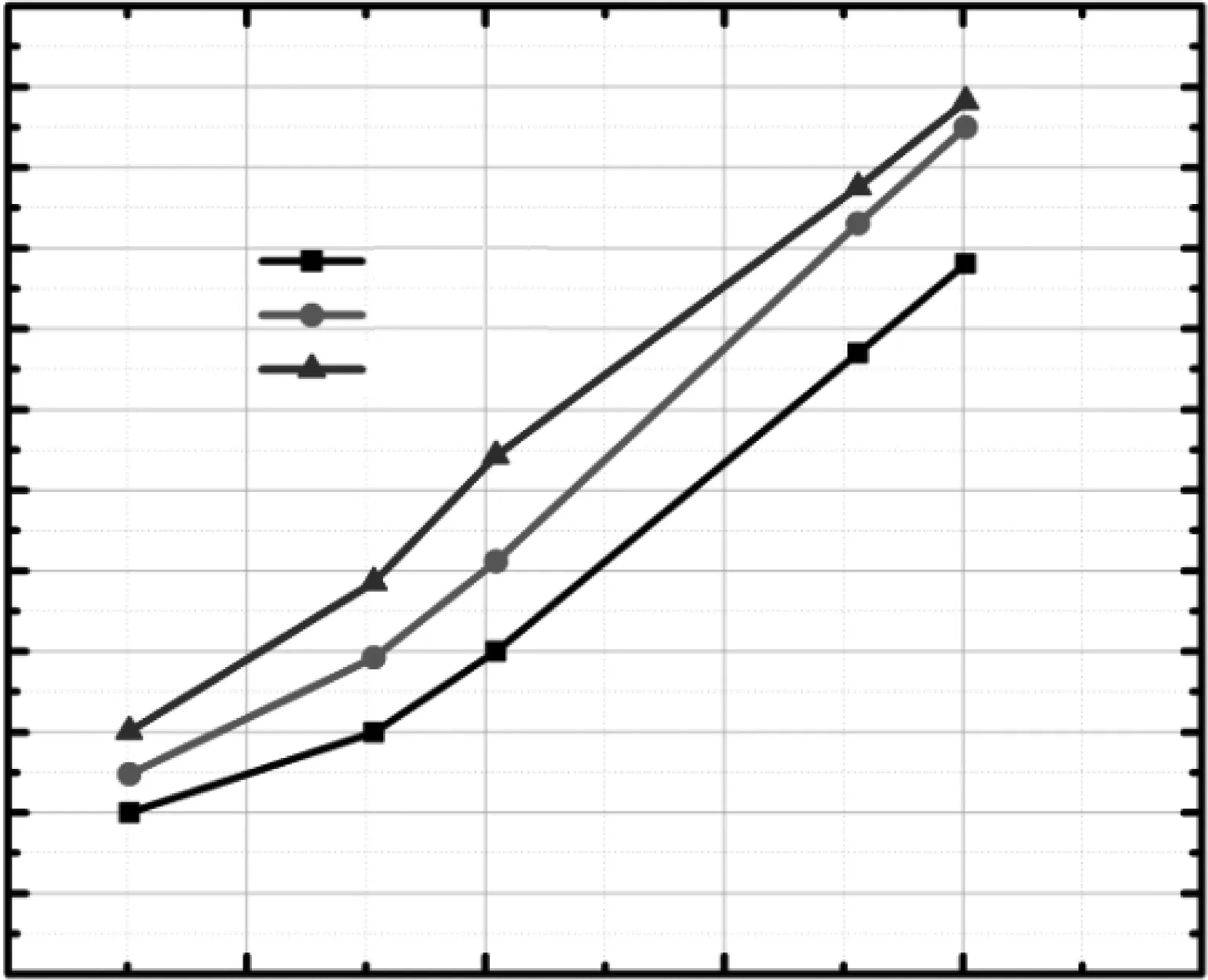
图5 3种不同算法的失真率曲线

3 本文多图像并行加密算法设计

本文加密算法示意图见图6。从图中可知，本文算法包括了3个阶段：复用阶段、复合图像置乱阶段、双重加密阶段。通过复用技术，同步完成对多个明文压缩与初始置乱；复合图像置乱阶段可彻底改变置乱图像的像素位置；根据混沌掩码与FrFT(FractionalFourierTransform)函数对二次置乱复合图像进行扩散。通过构造“复用技术处理—二次置乱—双重加密”结构，使密文获得良好的混乱性能；并保证了解密质量，显著提高算法的安全性。

图6 本文多图像同步加密算法示意图

1)若4幅明文的尺寸均为M×N，利用本文设计的复用技术对其进行同步压缩与置乱，获取复合置乱图像P。

2)设置好二维Arnold混沌映射的初值(x0,y0)，迭代M×N次，得到一个数组L={(X1,Y1),(X2,Y2),…,(XM×N,YM×N)}。二维Arnold混沌映射模型如下

(13)

式中：X,Y均为状态参数；x,y系统参数；mod代表求余运算。

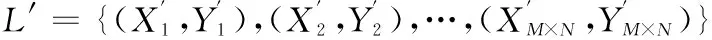
(14)

(15)

5)利用步骤4)中的位置集合S={S1,S2,S3,S4,…,SM×N}对复合置乱图像P进行二次置乱，得到图像P′，彻底充分扰乱像素位置。

6)输入初始值y0，迭代Logistic映射，产生混沌相位掩码CPRM1=(x,y)，见图7。再结合FrFT(Fractional Fourier Transform)变换，形成正则函数LCT

(16)

式中：f(x,y)代表输入图像；A代表复杂常量；CPRM1(x,y)代表混沌相位掩码。

图7 混沌相位掩码

Logistic映射模型如下

xi=μxi-1(1-xi-1)

(17)

式中：μ为控制参数，μ∈[0,4]。

7)根据加密函数，对二次置乱图像P′进行扩散，输出密文P″。加密函数如

P″=LCT[P′exp(iπ(CPRM1))]

(18)

式中：P″代表密文；P′代表二次置乱复合图像；LCT为正则函数。

因解密为加密的逆过程，故本文不做详细介绍。

4 仿真结果与分析

4.1 多图像加密效果

借助MATLAB仿真实验测试本文算法的安全性能。以4幅大小为233×233的明文图像为对象，见图8a～图8d。1D Logistic映射的初值x0=0.52，μ=1.3；2D Arnold映射初值为x0=0.35,y0=1.46；复杂常量A=3。利用本文多图像加密机制，对其进行加密，仿真结果见图8。经过本文设计的复用技术同步压缩与置乱后，得到复合置乱图像，见图8i；再由二维Arnold映射二次置乱后，复合图像得到了充分扰乱，见8k；最终得到密文，见图8l。由图8可知，4个明文图像的直方图分布很不均匀，波动剧烈，表明它们的随机性不强，安全性不高，见图8e～图8h。经过复用技术处理后，压缩为一个复合置乱图像，其像素点分布与初始明文，相差不大，见图9a；经过二次置乱后，相位位置彻底打乱，其像素点分布较前者而言，有一定的改善，但是还没达到理想状态，见图9b；经过混沌掩码的双重加密后，4幅图像的像素点分布趋于一致，而且较为均匀，见图9c。实验表明本文算法具有较高的安全性。

图8 本文算法加密效果

图9 本文算法直方图测试结果(灰度等级：0～256)

4.2 算法敏感性能分析

优异的加密机制应迎合“雪崩效应”。当密钥发生微小波动时，所产生的解密图像是截然不同的。本文测试了Logistic映射初值x0的敏感度，通过增加或减去δ=10-16来改变x0。即：(x0-δ)与(x0+δ)。用不同的密钥对图8l进行解密；并测试了x0的均方差MSE曲线，仿真结果见图10。从图10a与图10b可知，当x0发生极其微小变动时，是无法解密的，得不到初始明文图像的；且x0发生微小扰动时，其MSE曲线变化非常剧烈，见图10d。这表明本文算法具有较强的敏感性能。

图10 算法敏感度测试结果

4.3 解密质量对比分析

为了凸显本文算法的优越性能，本文设立了两个对照组：1)文献[8]，记为A；2)文献[9]，记为B。仿真结果如图11所示。从图中可以看到，虽然从视觉上，A、B两种多图像加密机制得到的解密图像是可以接受的，但是其解密效果不佳，都存在一定的模糊现象，这主要是由于A、B算法在将多个图像压缩成复合图像时，编码率得不到有效控制，且串扰效应明显，造成失真值较大，见图11a～图11b。而本文算法设计了率失真控制优化技术，有效控制编码率，继而有效解决了串扰效应与失真问题，见图11c。

图11 不同算法的解密效果分析

5 结论

本文基于DCT(Discrete Cosine Transform)变换与ZigZag扫描，设计复用技术，将多个明文压缩成一个复合置乱图像；并引入结构相似度，设计率失真控制优化技术，嵌入复用技术中，优化失真值，控制图像压缩；提出了复用技术耦合率失真控制优化的多图像并行加密机制。有效解决了多图像加密机制存在串扰效应以及密文失真等难题。测试结果表明：本文加密机制高度安全，具备优异的加密质量与强烈的敏感性能；且与当前多图像加密机制相比，本文算法的解密质量更加优异，有效消除了串扰效应。

[1]牟宇飞，张文普，王志中.基于分形和骑士巡游的图像压缩加密算法研究[J].电视技术，2014，38(1)：30-33.

[2]周琳，杜广朝，邵明省.基于双随机编码正交映射的全息图像加密[J].电视技术，2013，37(1)：24-27.

[3]刘博文，柏森，刘程浩.基于骑士巡游的灰度图像加密压缩算法[J].电视技术，2012，36(9)：10-14.

[4]ZHANG G，LIU Q.A novel image encryption method based on total shuffling scheme [J].Opt.Commun.，2011(12)：2775-2780.

[5]MAO Y，CHUI C.A symmetric image encryption scheme based on 3D chaotic cat maps[J].Chaos，Solitons & Fractals，2011，21(18)：749-761.

[6]ABDULLAH A H，ENAYATIFAR R，LEE M .A hybrid genetic algorithm and chaotic function model for image encryption [J].AEU：Int JElectron Commun，2012，66(10)：806-816.

[7]张文全，周南润.基于非对称密码系统的多图像加密算法[J].光电子.激光，2012，22(7)：213-216.

[8]郭雨，柏森，阳溢.基于复用技术和数论的图像加密压缩同步算法[J].电视技术，2013，37(5)：33-37.

[9]龚黎华，曾邵阳，周南润.基于2D Arnold变换与频谱切割的彩色图像加密算法[J].计算机应用，2012，32(9)：2599-2602.

[10]黄孝建.基于结构相似度的高效视频编码感知率失真优化方法：中国，103607590A[P].2014-02-26.

[11]马国强.一种在视频图像压缩中对率失真进行优化的方法：中国，101521819B[P].2010-12-01.

[12]WANG Y，WONG K W，LIAO X，et al.A new chaos-based fast image encryption algorithm [J].Appl.Soft Comput.，2011，11(1)：514-522.

[13]WANG Zhen，HUANG Xia，LI Yuxia，et al.A new image encryption algorithm based on the fractional-order hyperchaotic Lorenz system [J].Chinese Physics：B，2013，22(1)：1-7.

陈 阳(1979— )，硕士，主研数字图像处理、音视频处理；

郑涵容(1983— )，女，硕士，主研数字图像处理、音视频处理。

责任编辑：时 雯

Study on Multi-Image Encryption Mechanism Based on Multiplexing Technology Integration with Rate Distortion Optimization

CHEN Yang1，ZHENG Hanrong2

(1.TechnologyCenterofMultimedia，ZhejiangUniversityofMediaandCommunications，Hangzhou310014，China；2.DepartmentofcomputerEngineering，ZhejiangVocationalAcademyofArt，Hangzhou310014，China)

In order to overcome these defects such as crosstalk effects and distortion in current multi-image encryption mechanism，the multi-images parallel encryption algorithm is proposed based on multiplexing technology integration with rate distortion optimization controlling.The multiplexing technology is designed based on DCT(Discrete Cosine Transform)and ZigZag Scanning to take multi-images into one composite permutation image.And the Structural similarity is introduced to design the rate distortion controlling optimization method to embed into the multiplexing technology for optimizing the value of distortion to reduce the distortion.Then 2D Arnold map is used to per mutate the composite permutation image.The double encryption function is constructed by chaos phase mask to diffuse the permutation image.Simulation results are showed that this encryption mechanism is highly secure with excellent quality and strong key sensitivity, compared with current multi-image encryption algorithm，the decryption effects of the mechanism in this paper is best to effectively eliminate the crosstalk effects.

multi-images parallel encryption； multiplexing technology； rate distortion controlling； chaotic masks； crosstalk effects

【本文献信息】陈阳，郑涵容.复用技术耦合率失真优化的多图像加密机制[J].电视技术,2015，39(3).

TP391

A

10.16280/j.videoe.2015.03.005

2014-03-16