利用梯度方向的Hausdorff距离配准红外和可见光图像

冯晓磊，吴 炜，李 智，邓 文

(1.四川大学 电子信息学院，四川 成都 610064；2.西南电子设备研究所，四川 成都 610036)

利用梯度方向的Hausdorff距离配准红外和可见光图像

冯晓磊1，吴 炜1，李 智1，邓 文2

(1.四川大学 电子信息学院，四川 成都 610064；2.西南电子设备研究所，四川 成都 610036)

基于Hausdorff距离的算法已经被广泛应用于异源图像配准，但是现有的Hausdorff距离配准算法是在整幅图像上找最相近的点对，不仅容易出现错误匹配的情况，而且计算量很大。为了减少计算冗余和消除误配情况，提高配准的准确度，提出了一种利用梯度方向的Hausdorff距离配准算法。在进行配准时，将提取到的角点集合按照每个角点的不同梯度方向角分解为8个子集合。然后计算两幅图像中同一方向区间所对应的两个子集合间的Hausdorff距离。由于只在对应的子集合内找最相近的配准点对，减少了干扰点的数目和计算的次数，提高了计算的有效性和异源图像配准的准确度。实验结果表明，利用梯度方向的Hausdorff距离算法能够较好地运用于红外图像和可见光图像的配准，并且表现出较好的准确度和稳健性。

异源图像；Hausdorff距离；梯度方向；Harris角点

在现代战争和现代医学领域中，为了获得最佳的作战效果和快速准确的诊断，通过单一传感器获得的信息，已经无法满足需要。如果通过多个传感器，能够获得更全面的信息，对战略决策和病情诊断会有重大意义。红外图像利用在夜间正常工作的优势，在军事领域有重要的作用。而且红外图像在医学康复领域也有重要的作用，但是含有较多的噪声，经常需要和可见光图像结合，才能获得更多、更全面的信息。

红外图像得到的是热图，灰度值是图像的温度特征，其中阴影部分在红外图像中是无法显示的；可见光图像的灰度，是由物体对光的反射和阴影部分决定的。红外图像和可见光图像缺少共同的信息，同时也使二者具有互补作用。红外图像能克服部分视觉上的障碍而探测到目标和夜间能够正常成像，成为检测设备的必需品，但是红外图像中有较多的噪声；而可见光图像中有较少的噪声，但是在夜间是无法正常成像的。这种互补的作用，使红外图像和可见光图像的融合后能够获得更为全面的信息，但是图像配准是图像融合必不可少的步骤[1-3]。

目前常用的异源图像配准方法可分为基于像素的算法和基于特征的算法，基于像素的算法适用于两幅图像的灰度分布间存在一定相关性的图像；基于特征的算法适用于结构明显的图像。在实际应用中基于特征的算法在大多数情况下有很好的配准效果[4]。如果两幅图像的特征被正确提取出来，这些方法能够容易找到配准变换参数[5]。但是在大多数情况下，红外图像和可见光图像有不同的信息特征，并且有一些重要的特征不容易同时提取到。无法在两幅图像中同时提取到重要信息，致使配准结果出现误配。只有尽可能地增强容易提取的特征信息的相关性或者寻找更好的提取特征的方法，才能有效提高配准的准确度。

常用的特征点有角点和边缘点。由于在红外和可见光图像中某些边缘不是同时存在的，使提取到的边缘点往往缺乏共同信息；并且选择边缘点特征，获得的边缘点数目会比较多，使计算量大并且过程比较复杂；角点具有几何图形不变性，能够通过人工观测很好地分辨[6]提取出的角点是否合理正确，对比异源图像中提取到的角点是否有共性；可以通过观察提取到的角点的分布特点，进行参数修改，使其达到最佳效果，所以文章选用了角点特征。

基于两个点集间的Hausdorff距离匹配算法用起来比较简便，不需要建立两点之间的对应关系，而是计算两个点集之间的距离。由于其计算过程的简便性，已被广泛用于异源图像的配准[7]。Huttenlocher在基本Hausdorff距离的基础上提出了Partial Hausdorff距离算法(P-HD)[8]，解决了部分遮挡和虚假点的问题。Dubuission提出了modified Hausdorff 距离(modified-HD)[9]，具有更强的分辨能力。Sim等人在modified-HD基础上进行进一步的改进，提出了以M-estimation为基础的 Hausdorff Distance算法(M-HD)[10]，利用消费函数(Cost Function)减少了边缘外部点的作用。Oh-Kyu等人提出了Accurate M-Hausdorff距离(AM-HD)，采用距离方向变换(Distance Orientation，DO)[7]能够准确地检测外部点，提高配准的准确度。以上这些方法都是利用图像的边缘点集合进行计算，WU Jianming等人提出了一种改进的Hausdorff距离算法[11]，此算法用的是角点集合进行计算，利用几何结构限制条件，有效地从最初配准的点对中检测出误配的点对。但是由于异源图像中提取的特征点相关性较差，导致经过多次的计算得到的配准点对未必是正确的配准，误配情况的存在，造成了计算的浪费，并且降低了配准的准确性。

以上算法大多是用边缘点集合直接进行计算Hausdorff距离进行配准，这样的算法是在整幅图像上寻找配准的点对，盲目的寻找使计算量很大；对于同样的图像，提取的边缘点要比角点多，所以在所有的边缘点中寻找距离相近的点对，相对于在角点中找配准的点对而言，干扰点较多，大量的干扰点会使配准结果的准确度降低。

针对这个问题，本文提出了利用梯度方向信息的Hausdorff距离算法。该方法首先从图像中提取角点，对提取到的角点集合按照每个角点的梯度方向角所在的角度区间不同进行分类；然后计算两幅图像中位于同一个区间所对应的子集合间的利用梯度方向信息的Hausdorff距离；计算得到各个子集合间的距离后，采用均值的方法，只计算较小的K个子集合间的距离的均值，将均值作为最终的距离值。通过实验证明：利用梯度方向信息的Hausdorff距离算法对于红外图像和可见光图像的配准不仅位置误差有所减小，而且比其他的方法更加集中在实际配准位置附近。由此看出，本文中提出的算法，在红外图像和可见光图像配准中有更好的准确度。

1 Hausdorff距离研究现状

HD(P,Q)=max(h(P,Q),h(Q,P))

(1)

前向距离计算公式为

(2)

后向距离计算公式为

(3)

(4)

式中：p和q分别是P和Q中的任意点。每种算法只提到了前向距离的算法，后向距离的算法与前向距离的算法一样，只需要把两个点集的位置互换即可。由于Hausdorff距离计算的是最小最大距离，即使P和Q形状非常相似，只要P中有一个点到Q的距离较远，计算出的距离会很大[12]。由此看出，原始的Hausdorff距离对噪声点和边缘外部点会比较敏感，在用于图像配准算法时会影响配准的效果。

(5)

Dubusssion提出的modified-HD算法[6]，用所有点的均值距离作为配准距离，由于均值是数据的集中趋势的量数。由于对所有的点距离取均值，使噪声点和外部点对结果的影响变小。modified-HD的前向距离hm(P,Q)为

(6)

Sim等人提出的基于最大似然值(Maxmumlikelihood-estimation，M-estimation)的M-HD算法[10]，利用成本函数(Costfunction)U(·)函数中的阈值，当最小距离大于阈值时，其距离值被赋值为阈值；小于阈值时，距离值不变。噪声点和外部点对应的最小距离比较大，通过成本函数后，消除了外部点和噪声点的影响，提高了配准的准确性。M-HD定义前向距离hM(P,Q)为

(7)

成本函数U(·)被定义为

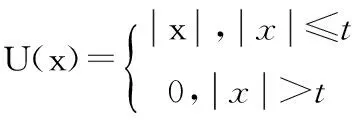
(8)

Oh-Kyu Kwon等人提出了AM-HD算法[7]，该算法利用距离变换和方向变换，先对二值图进行距离变换，然后对得到的距离变换图再进行方向变换。通过二者的混合使用，能够准确地分辨异常值[6]，AM-HD算法定义前向距离hAM(P,Q)为

(9)

(10)

式中：D(i,j)是经过距离变换得到的灰度图；N是P中特征点的个数；kn是Kirsch算子[13]中的第n个方向的模板，n=0,1,2,…,7；δ(·)是冲激函数，计算如下

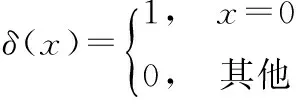
(11)

以上各种Hausdorff距离配准算法，为了找配准的点对，需要计算两幅图像中任何两点间的距离，存在一定的盲目性。在参考图像中的每一个角点与待配准图像中配准的点，只有一个是正确的，其他的点都是干扰点，所以盲目寻找配准点对存在的干扰点数目较多。由于大量干扰点的存在，使配准点对出现误配的情况可能性较大，导致配准的准确性降低，而且盲目性导致计算过程的浪费。

2 利用梯度方向信息的Hausdorff距离算法

针对以上的问题，文章中提出了一种利用梯度方向信息的Hausdorff距离配准算法，首先通过角点的梯度方向角的不同，对点集合进行划分，将梯度方向角位于同一个方向区间的角点组合为一个子集合；然后计算对应点集合间的距离，缩小了寻找范围，减少了在找最相近点对的计算量，同时消除了不同区间对应子集合中点的干扰，提高了计算的有效性。利用梯度方向信息的Hausdorff距离算法与现有的Hausdorff距离算法的本质区别，如图1所示。由于每个角点都对应一个梯度方向角，所以每个角点都可以在极坐标平面内找到对应的位置，在图1中将从参考图像和待配准图像中提取到的初始角点集合，分别显示在两个极坐标平面上。假设图1a和图1b中左边的是从参考图像中提取到的角点在极坐标的分布图，右边是从待配准图像中提取到的角点在极坐标的分布图，现有的算法是在所有的角点中寻找配准的点，而利用梯度方向信息的Hausdorff距离算法只在梯度方向角度位于同一个区间的点中寻找配准点。

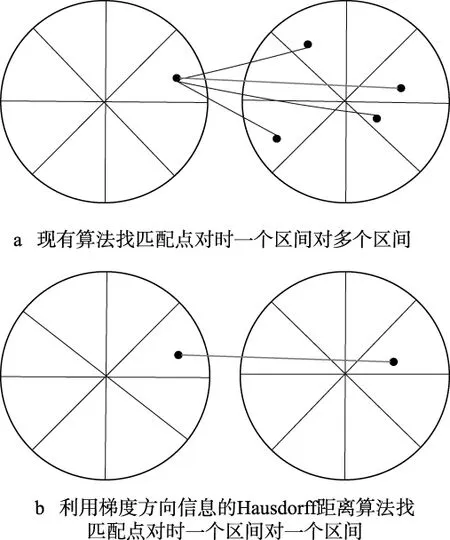
图1 现有算法和利用梯度方向信息的Hausdorff距离算法的本质区别

2.1 角点提取和角点集合的分解

现有的Hausdorff算法大多是选择边缘点进行计算的，然而红外和可见光图像中，某些边缘不是在两幅图像中同时存在的，所以使二者边缘点集间的共性信息减少。一般情况下，提取的边缘点很多，所以在计算时，要进行很多次的重复计算前向和后向距离，使计算量大大增加。本文中选择角点集合进行计算，利用Harris检测算子提取角点。通过角点检测后，可得到二值图像。

利用Sobel算子计算图像每个像素的梯度方向，将图像的灰度值用其梯度方向角度代替，即相当于将图像的梯度方向可视化。角点梯度方向可视化过程为

IPO=IP*IO

(12)

式中：IP是图像提取角点后得到的二值图像；IO是图像的像素梯度方向角可视化图像；*代表将两矩阵对应元素相乘运算。计算梯度方向时，Sobel算子模块为

(13)

(14)

利用Sobel算子的模板与图像I进行平面卷积，可以得到横向亮度差分近似值Ix和纵向亮度差分近似值Iy，由这两个近似值可计算梯度方向Gor为

(15)

对于异源图像，在可见光图像中提取到的特征点，在红外图像中未必可以提取到对应的相关特征点。现有的Hausdorff距离算法是在整幅图像上找最相近的点对作为配准的点对，计算两个点集的相似度，对于每个点的辨别能力较差，这样导致了计算的浪费和配准的准确性下降。为了减少计算量，提高计算的有效性；减少误配的点对配准的情况，提高配准的准确性，要尽可能缩小寻找配准点对的范围和减少干扰点的影响，有针对性地找最相近点对。在文献[3]中对异源图像的梯度幅值、梯度方向和灰度值3个量的相关性进行了对比实验，结果显示异源图像中梯度方向有较大的相关性，在文章中就利用了异源图像梯度方向间的相关性，在角点位置信息的基础上，增加了其梯度方向信息，利用方向信息对初始角点集合分解。

为了解决盲目配准的问题，采用分解初始的角点集合的方式，将初始的点集合划分成8个带有方向性的子集合，这样只在同一个方向的子集内找最相近点对，消除了不同方向的点的干扰，减少了误配的可能性。以一个像素点为中心，周围有8个相邻的像素，文章中根据这8个像素所覆盖的角度范围，将梯度方向角划分了8个区间。具体做法是：1)计算角点梯度方向图；2)将-180°～+180°的角度区间均分为8子区间；3)将角点中位于一个子区间的角点合并为一个子集合，这样就产生了8个子集合。图2给出了角度区间的划分方法，具体为：(-22.5°～22.5°)，(22.5°～67.5°)，(67.5°～112.5°)，(112.5°～157.5°)，(-157.5°～-112.5°)，(-112.5°～-67.5°)，(-67.5°～-22.5°) ，(157.5°～180°)∪(-180°～-157.5°)。

图2 梯度方向角8个区间划分方法

2.2 计算利用梯度方向的Hausdorff距离

假设经过对角点集合的分解后，红外图像中的8个点集合记为IRP={IRPi,i=1,2,…,8}，可见光图像中的8个点集合记为VISP={VISPi,i=1,2,…,8}。利用梯度方向的Hausdorff距离HGor定义为

(16)

式中：HDi(i=1,2,…,8)是按升序排列后的数列，i的8个值分别代表了8个不同的方向区间；K是一个小于等于8的常数，在这篇文章里，选择4作为K的值，进行了实验。这里的HDi=HD(IRPi,VISPi)，HDi是两幅图像中同位于第i个方向区间的角点集合间的Hausdorff距离。在计算HDi时，利用文献[11]中均值的算法，增加了限制条件，计算如下

(17)

(18)

(19)

式中：U(·)是成本函数；M和N分别是IRPi和VISPi中满足U(·)非零点的个数；irp和visp分别是IRPi和VISPi集合中的每个点元素；h(IRPi,VISPi)和h(VISPi,IRPi)分别是两个点集间的前向和后向距离。

3 实验结果

实验中使用异源图像来自于www.imagefusion.org网站的红外和可见光图像对。这些图像共有8对图像，分别对应8个不同场景，图3中给出了实验中用的图像。为了验证本文中提出的算法对红外图像和可见光图像配准的有效性，也将该算法与modified-HD，M-HD，AM-HD这3种算法进行了比较。在实验的过程中对可见光图像进行逐个角度的旋转和逐像素的平移，找到配准时的旋转角度和平移坐标。当距离最小时，对应的平移坐标和旋转角度即是计算出来的配准结果。

图3 测试使用的异源图像

为了分析在旋转θg0=10，平移(xg0,yg0)=(5,5)的情况下，4种算法配准时的平移变换坐标和旋转角度的准确度，定义了误差距离Errdist和误差角度Errori，二者的计算如下

(20)

(21)

式中：(x,y)是每对图像经计算得到的配准位置；θ是计算得到的旋转角度。除了计算每种算法的误差外，还定义了平移坐标和旋转角度的离散度，离散度用来衡量配准的位置参数与实际的配准参数的偏离程度和稳定程度，平移和旋转的离散度σdist，σori分别定义如下

(22)

(23)

式中：L是实验的图像对数；(xi,yi)和θi分别是第i对实验图像计算得到的平移位置和旋转角度。根据以上的定义，实验中用8对红外图像和可见光图像进行了实验，统计了每一对异源图像的配准误差和4种算法配准结果的离散程度。图4是平移变换配准时的误差距离的曲线，利用梯度方向信息的Hausdorff距离算法的配准效果modified-HD，M-HD和AM-HD有明显的提高，不仅配准的对数有所增加而且误差也有所减小。图5给出的是误差角度曲线，虽然对于前面几对图像，利用梯度方向信息的Hausdorff距离算法和M-HD，modified-HD的误差是一样的，但是在后面的几对图像中角度误差明显有所减小；而利用梯度方向的Hausdorff距离的算法和AM-HD算法得到的配准角度都是准确的。

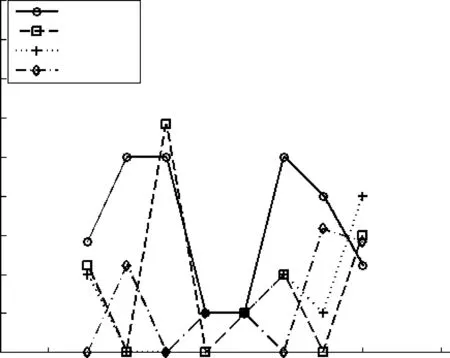
图4 旋转误差比较

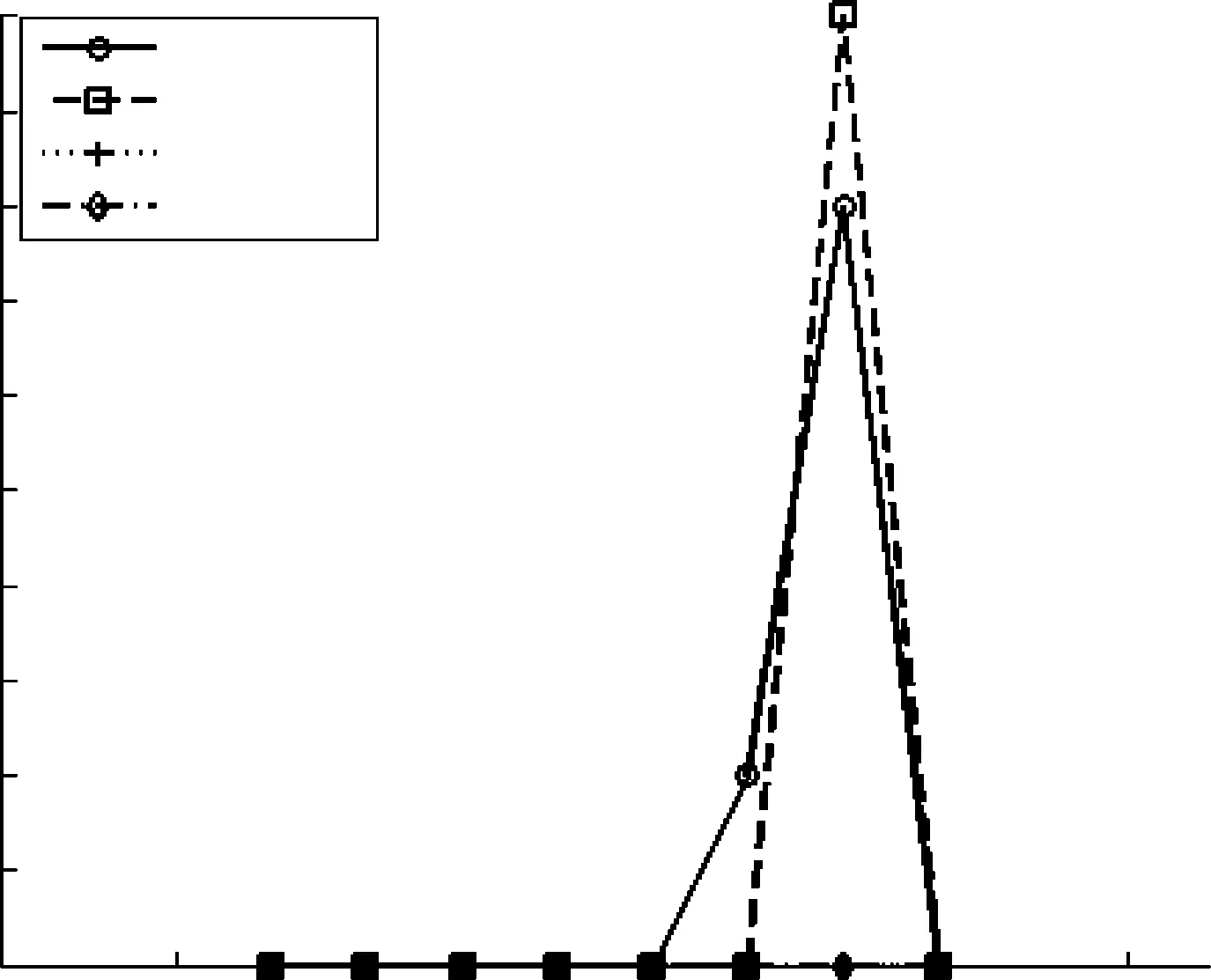
图5 平移误差比较

图6和图7分别给出了平移变换和旋转变换的离散度，根据离散度的定义，可以得知：离散度越小，集中程度会越高，算法的稳健性会越高。由图6也可以看出利用梯度方向信息的Hausdorff距离配准算法在做平移变换时的离散度远远小于modified-HD和M-HD两种算法，与AM-HD算法相比较离散度也是有降低的，说明利用梯度方向信息的Hausdorff距离配准算法的配准结果的位置相对比较集中，主要分布在离实际配准位置较近的区间里，准确性相对来说是较好的。图7给出的是旋转变换时的离散度，利用梯度方向信息的Hausdorff距离的配准算法与M-HD，modified-HD相比，明显离散度是最小的，与AM-HD的准确度是一样的。

图6 平移离散度比较

图7 旋转离散度比较

平移和旋转都是图像间常见的变换，所以综合来看，对于旋转变换和平移变换，利用梯度方向信息的Hausdorff距离的配准算法比其他的四种算法相比，不仅配准位置误差较小，而且离散度也是最小的，说明利用梯度方向信息的Hausdorff距离的配准算法的配准结果相对是比较准确的，并且配准结果是相对集中在实际配准位置附近的，有较好的稳健性。

在不同的初始变换下情况下，还进行了4种算法的平移和旋转的平均误差的比较实验，平均平移误差计算如下

(24)

(25)

式中：n是初始变换的个数。旋转采用了θg0=10，θg1=20，θg2=30这3个初始变换，计算了每种算法的平均误差角度值；平移采用了(xg0,yg0)=(5,5)，(xg1,yg1)=(10,10)，(xg2,yg2)=(15,15)这3个初始变换。图8和图9分别给出了不同的初始变换下，每对图像的平移和旋转变换的误差值。

图8 每对图像在3次不同的初始平移变换的平均误差

图9 每对图像在3次不同的初始旋转变换的平均误差

从图8看出，在平移变换时，利用梯度方向的Hausdorff距离的误差与其他3种方法相比，有更多的完全配准对数，平均误差总体较小。图9中显示，基于梯度方向的Hausdorff距离算法和AM-HD算法在旋转时平均误差一样，比M-HD和modified-HD算法有更小的平均误差。由此可以看出，无论是平移变换还是旋转变换，利用梯度方向的Hausdorff距离算法比M-HD，modified-HD的平均误差小；和AM-HD算法相比，虽然旋转时AM-HD和利用梯度方向的Hausdorff算法的平均误差一样，但是在平移时AM-HD却不如文章中提出的算法，因此利用梯度方向的Hausdorff距离的算法比AM-HD好。总体来说，利用梯度方向的Hausdorff距离算法的误差比较小，有更好的准确度。

4 结论

针对现有的Hausdorff距离配准算法，盲目地在整幅图像上寻找配准点对问题，本文提出了利用梯度方向信息的Hausdorff距离的异源图像配准算法。该算法计算每个角点的梯度方向角，利用角度值所位于的角度区间不同，将提取到的初始的角点集合分解为8个子集合，每个子集合中的角点都是梯度方向位于同一个角度区间的点。在进行配准计算时，只计算两幅图像中同一个角度区间所对应的子集合间的距离，这样就消除了不同角度区间的点对配准结果的干扰，通过大大减少了干扰点的数目，减少了误配的情况，提高配准的准确度。通过实验，证明了利用梯度方向信息的Hausdorff距离算法有较小的配准误差，说明其能更好地实现红外图像和可见光图像间的配准而且有更高的配准精度。

[1]HUANGXP，NETRAVALIR，HONGM，etal.Multi-sensorfusionofelectro-opticalandinfraredsignalsforhighresolutionvisibleimages[J].Oceans，2012，12(8)：1-6.

[2]EISLERK，HOMMAC，GOLDAMMERM，etal.Fusionofvisualandinfraredthermographimagesforadvancedassessmentinnon-destructivetesting[J].ReviewofScientificInstruments，2012，84(6)：1-5.

[3]葛小青.红外与可见光图像融合的研究[D].重庆：重庆大学，2010.

[4]HANJG，ERICJP，ZEEUWP.Visibleandinfraredimageregistrationinman-madeenvironmentsemployinghybridvisualfeatures[J].PatternRecognitionLetters，2013，34(1)：42-51.

[5]KIMYS，LEEJH，RAJB.Muti-sensorimageregistrationbasedonintensityandedgeorientationinformation[J].PatternRecognition，2008，41(11)：3356-3365.

[6]BARBARAZitova，JANFlusser.Imageregistrationmethods：asurvey[J].ImageandVisionComputing，2003，21(11)：977-1000.

[7]KWONOK，KIMDS，SUHJW.AccurateM-Hausdorffdistancesimilaritycombiningdistanceorientationformatchingmulti-modalsensorimages[J].PatternRecognitionLetters，2011，32(7)：903-909.

[8]HUTTENLOCHERDP，KLANDERMANGA，RUCKLIDGEWJ.ComparingimagesusingtheHausdorffdistance[J].IEEETrans.PatternAnalysisandMachineIntelligenc，1993，15(9)：850-863.[9]DUBUISSON M P，ANIL K J.A modified Hausdorff distance for object matching[C]//Proc.International Conference on Pattern Recognition，1994.[S.l.]：IEEE Press，1994：566-568.

[10]SIM D G，KWON O K，PARK R H.Object matching algorithms using robust Hausdorff distance measures[J].IEEE Trans.Image Processing，1999，8(3)：425-429.

[11]WU J M，JING Z L，WU Z，et al.Study on an improved Hausdorff distance for multi-sensor image matching[J].Common Nonlinear Sci.Numer Simulat，2012，17(2)：520-531.

[12]牛力丕，毛士艺，陈炜.基于Hausdorff距离的图像配准研究[J].电子与信息学报，2007，29(1)：35-38.

[13]KIRSCH R A.Computer determination of the constituent structure of biological images[J].Computer and Biomedical Research，1971，4(3)：315-328.

[14]YANG W P，WANG X Z，MORAN B，et al.Efficient registration of optical and infrared images via modified Sobel edgeing for plant canopy temperature estimation[J].Contents and Electrical Engineering，2012，38(5)：1213-1221.

[15]BILODEAU G，TORABI A，MORIN F.Visible and infrared image registration using trajectories and composite foreground images[J].Image and Visible Computing，2011，29(1)：41-50.

责任编辑：时 雯

Hausdorff Distance Using Gradient Orientation Registers Infrared and Visible Image

FENG Xiaolei1，WU Wei1，LI Zhi1，DENG Wen2

(1.CollegeofElectronicInformation，SichuanUniversity，Chengdu610064，China；2.ElectronicequipmentResearchInstituteofSouthwestChina，Chengdu610036，China)

Hausdorff distance has been widely used to register multi-sensor images.The traditional Hausdorff distance finds the nearest point pairs in the full image.It not only leads to matching error but also leads to that the computational complexity is very high.In this paper，an image registration algorithm，Hausdorff distance using gradient orientation information，is proposed to reduce computational complexity and enhance the precision of registration.Firstly，the proposed method divides the initial corner point set into 8subsets using the different gradient orientation information.Then Hausdorff distances between the two subsets which have the same direction range in the two images are computed.Since corner points only match its corresponding points in a corresponding subset，it decreases the number of the points of matching error，and the computation time.The experimental results show that the proposed method performs well to register infrared image and visible image，and has better precision and robustness compared with other methods.

multi-sensor image；Hausdorff distance；gradient orientation；Harris corner

【本文献信息】冯晓磊，吴炜，李智,等.利用梯度方向的Hausdorff距离配准红外和可见光图像[J].电视技术,2015，39(3).

国家自然科学基金项目(61271330)；四川省科技支撑计划项目(2014GZ0005)；归国人员留学基金项目

TP391.4

A

10.16280/j.videoe.2015.03.002

2014-03-03