楔形中心和偏心料仓中壁面摩擦系数对卸料速率的影响

许鹏凯，段学志，钱刚，周兴贵



楔形中心和偏心料仓中壁面摩擦系数对卸料速率的影响

许鹏凯，段学志，钱刚，周兴贵

（华东理工大学化学工程联合国家重点实验室，上海200237）

采用离散元方法（DEM）研究了在不同的内摩擦系数、料仓半锥角和料仓宽度条件下，楔形中心料仓和偏心料仓中壁面摩擦系数对卸料速率的影响。研究发现，随着壁面摩擦系数的增加，两种料仓的卸料速率均先降低后稳定。当料仓从中心料仓变为偏心料仓时，壁面摩擦系数对卸料速率的影响程度以及卸料速率停止下降时的壁面摩擦系数的值都增大。随着内摩擦系数的减小或料仓半锥角的增大，壁面摩擦系数对卸料速率的影响程度以及卸料速率停止下降时的壁面摩擦系数的值都逐渐减小。增加料仓宽度能够削弱壁面摩擦系数对卸料速率的影响程度，但并不改变卸料速率停止下降时的壁面摩擦系数的值。

颗粒流；计算机模拟；实验验证；卸料速率；壁面摩擦系数

引 言

矩形截面的料仓由于其较低的制造成本和较高的空间利用率等优点而被广泛应用于工业生产过程[1-3]。为了避免在卸料过程中形成死区，料仓通常采用楔形的底部结构[4]。根据出料口位置，这种楔形料仓可分为中心料仓和偏心料仓。前者的结构 较为简单且在设计时较为容易[5]。然而，在设备空间受限或是与其他设备耦合时有特殊要求的情况下，中心料仓并不适用，采用偏心料仓则可以满足要求[6]。

在料仓的设计和操作中，准确地预测卸料速率非常重要[7-9]。目前的研究结果表明，颗粒内摩擦系数、料仓半锥角和出料口位置等因素均对卸料速率有显著影响[6,10-13]。然而，关于壁面摩擦系数对卸料速率的影响目前还未得出一致结论。Langston等[14]的工作中指出卸料速率对壁面摩擦系数较为敏感，而Kruggel-Emden等[15]、Ketterhagen等[6]则得出相反的结论。此外，随着壁面摩擦系数的增加，卸料速率减小[15]、保持不变[16-17]甚至增加[18]的结果都被报道过。实际料仓中，壁面摩擦系数随着壁面粗糙度等因素的变化而变化[19]。为了准确地预测卸料速率，有必要系统地研究壁面摩擦系数对卸料速率的影响。

在对颗粒流动的研究中，离散元方法（DEM）已被广泛应用[20-22]。通过这种方法所得到的结果与实际情况能较好地吻合[15,23-27]。本文采用DEM研究了楔形中心料仓和偏心料仓中壁面摩擦系数对卸料速率的影响。在此基础上，还进一步研究了颗粒内摩擦系数、料仓半锥角和料仓宽度等因素对上述影响的作用。通过分析料仓中颗粒流动的变化提出了以上变化发生的机理。

1 DEM模拟方法

本工作模拟了三维（3D）矩形截面料仓中的颗粒流动。料仓结构如图1所示。该料仓的厚度和出料口宽度分别为9倍和5倍颗粒直径。料仓的其他参数以及颗粒的性质如表1[15]所示。在默认条件下，颗粒内摩擦系数（i）为1.376，料仓半锥角（w）为30°，料仓宽度（hopper）为0.10 m。偏心料仓的出料口紧靠左侧壁面。图1中彩色颗粒为示踪颗粒。这种颗粒与其他颗粒除颜色不同外，其他性质都相同。

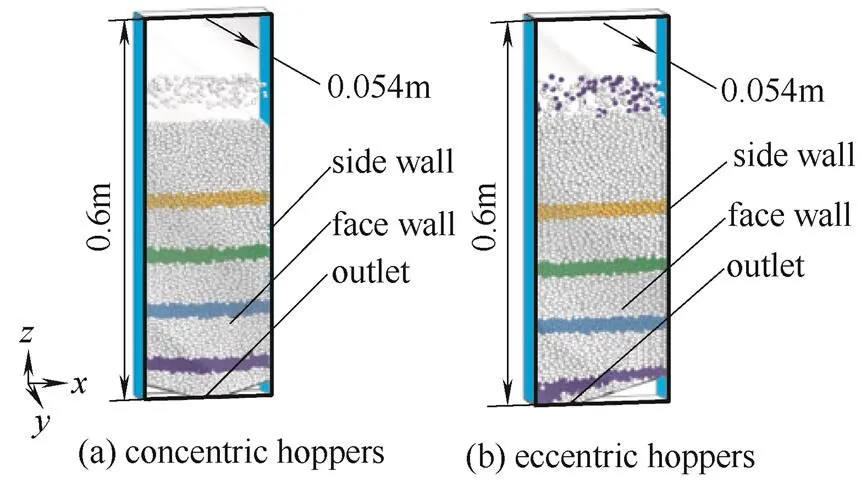
图1 模拟计算中所用料仓的结构

表1 颗粒物性以及料仓的相关参数

DEM最早由Cundall等[28]提出。该模拟过程主要包含4个步骤：颗粒系统的生成、颗粒间碰撞的搜索、碰撞作用力的计算以及颗粒系统的更新[29]。本工作采用En masse方法将颗粒填充到料仓中以形成颗粒系统[30]。颗粒之间以及颗粒与壁面之间的作用力均通过线性模型进行计算[15]。更新颗粒系统时，需对颗粒的线性运动和转动进行更新。这两种运动可以用方程式（1）和式（2）进行描述

式中，、为任意颗粒；和分别为颗粒的质量和转动惯量；和分别为颗粒的线速度和角速度；为由颗粒指向接触点的向量；g,i和c,ij分别为颗粒的重力以及颗粒、之间的碰撞作用力。

对于本工作所用料仓，其侧壁由垂直和倾斜壁面组成，而面壁则仅由垂直壁面组成。侧壁结构（如侧壁倾斜壁面的倾角）的变化可以改变料仓中的颗粒流动行为，进而改变壁面摩擦系数对卸料速率的影响。在本工作中，面壁摩擦系数（face）固定为0.1，而侧壁摩擦系数（side）在0.2～1.2之间变化，以更全面地理解壁面摩擦系数对卸料速率的影响。

2 结果与讨论

2.1 DEM实验验证

本工作采用文献中已报道的方法来验证模拟结果的可靠性，即比较模拟结果与实验结果中的平均卸料速率[15,30]。此处所用的颗粒及料仓与Kruggel-Emden等[15]工作中所用颗粒和料仓相同。通过本工作中的DEM程序模拟得到的卸料速率（）平均值为0.029 kg·s-1，与Kruggel-Emden等[15]报道的实验值（0.028 kg·s-1）基本一致，如图2所示。这说明本工作中的模拟结果是可信的。

图2 拟3D料仓卸料过程中卸料速率的演变过程（其中虚线表示平均卸料速率）

2.2 默认条件下壁面摩擦系数对卸料速率的影响

图3所示为默认条件下，中心和偏心料仓的壁面摩擦系数对卸料速率的影响。结果显示，随着壁面摩擦系数的增大，两种料仓的卸料速率都先降低后稳定。其中，偏心料仓中卸料速率的下降幅度（0.139 kg·s-1）以及其停止下降时的壁面摩擦系数的值（1.0）都比中心料仓中的结果（0.072 kg·s-1和0.75）更大。图4中给出了默认条件下，两种料仓中的示踪颗粒在卸料开始时和卸料过程中的分布。卸料开始时[图4 (a)、(f)]，同种示踪颗粒位于同一高度范围内。卸料一段时间（1.0 s）以后，当壁面摩擦系数为0.2时[图4 (b)、(g)]，两种料仓中的示踪颗粒几乎仍然保持在同一高度范围内。随着壁面摩擦系数的增加[图4 (c)～(e)，(h)～(j)]，壁面附近示踪颗粒的流动被逐渐减缓。这一结果与文献结果一致[31]。

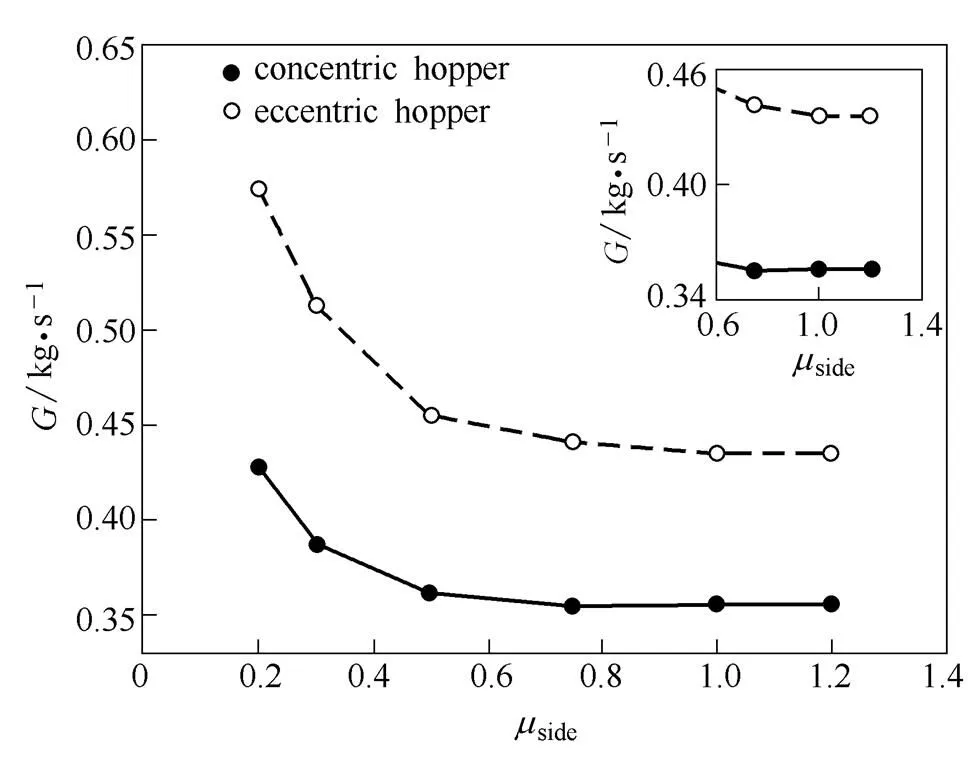
图3 在默认条件下中心料仓和偏心料仓的壁面摩擦系数对卸料速率的影响

图4 默认条件下中心料仓和偏心料仓中的示踪颗粒在卸料开始和卸料过程中的分布

颗粒的流动可以分为颗粒之间的相对滑动以及颗粒与壁面之间的相对滑动。壁面摩擦系数通过影响颗粒与壁面之间的相对滑动[31-32]，对卸料速率产生影响。在较小的壁面摩擦系数下，颗粒与壁面之间的相对滑动比颗粒之间的相对滑动容易发生。壁面摩擦系数的增加逐渐抑制了颗粒与壁面之间的相对滑动，并使其最终比颗粒之间的相对滑动难以发生。因此，卸料速率先降低后稳定。

在默认条件下，由于颗粒之间的互相挤压，壁面的倾斜以及颗粒间的支撑作用，颗粒在渐缩段中流动时受到较强的阻碍。因此，卸料速率主要由渐缩段颗粒流动控制。进一步地，渐缩段中的颗粒流动主要受渐缩段壁面摩擦系数的影响，进而使得渐缩段壁面对卸料速率的控制作用大于垂直段壁面对卸料速率的控制作用。图5结果显示，渐缩段壁面摩擦系数（sw）增大时卸料速率的变化幅度明显大于垂直段壁面摩擦系数（sv）增大时卸料速率的变化幅度。这一结果也说明渐缩段和垂直段壁面中，前者对卸料速率的控制作用较大。然而，在较小的壁面摩擦系数下，卸料速率并非完全决定于渐缩段颗粒流动。这是因为渐缩段内颗粒间的支撑作用并不足够强，增大壁面摩擦系数逐渐增强这一支撑作用。因此，渐缩段颗粒流动对卸料速率的控制作用越来越强，直至完全控制卸料速率。卸料速率停止下降时的壁面摩擦系数的值也完全决定于渐缩段中的颗粒流动。

图5 默认条件下中心和偏心料仓中不同段的壁面摩擦系数对卸料速率的影响

中心料仓和偏心料仓中壁面摩擦系数对卸料速率的影响有差异是因为两种料仓中的颗粒流动行为不同。当渐缩段的一个壁面由垂直壁面变为倾斜壁面时，即从偏心料仓变为中心料仓时，颗粒在流向出料口时所受到的阻碍作用被增强[6]。这一过程中，颗粒之间以及颗粒与该壁面之间的相对滑动都被抑制。随着颗粒流动的减缓，上层颗粒的载荷更多地由下层颗粒承担。这有利于颗粒之间以及颗粒与壁面之间的相对滑动，进而削弱这两种相对滑动所受到的抑制作用。相对于壁面上的颗粒，不与壁面接触的颗粒能够承担更大空间内的颗粒载荷。因此，这一向下传递的载荷更有利于削弱对颗粒间相对滑动的抑制作用。

根据以上论述，从偏心料仓变为中心料仓时，渐缩段中颗粒与壁面之间的相对滑动相对于颗粒之间的相对滑动被削弱。这一变化使得颗粒与壁面之间的相对滑动对颗粒流动的贡献减小。因此，中心料仓渐缩段壁面以及整个料仓的壁面，对卸料速率的影响都较小（图5）。此外，在这一变化的作用下，颗粒与渐缩段壁面之间的相对滑动在较小的壁面摩擦系数下就比颗粒间的相对滑动难以发生。故而，卸料速率停止下降时的壁面摩擦系数的值在中心料仓中比在偏心料仓中小。

上海诚达物流运输公司根据上海汽车变速器各部门的生产需要，将各零部件、半成品运输到指定的目的地，同时配合各生产单位进行卸货。

2.3 多种颗粒和料仓性质条件下壁面摩擦系数对卸料速率的影响

随着颗粒内摩擦系数、料仓半锥角和料仓宽度的变化，壁面摩擦系数对卸料速率的影响也产生变化，如图6所示。减小颗粒内摩擦系数[图6 (a)、(b)]或增大料仓半锥角[图6 (c)、(d)]都使得壁面摩擦系数对卸料速率的影响程度以及卸料速率停止下降时的壁面摩擦系数的值减小。增大料仓宽度能够减小壁面摩擦系数对卸料速率的影响程度，但并不改变卸料速率停止下降时的壁面摩擦系数的值[图6 (e)、(f)]。进一步的结果表明，颗粒内摩擦系数的减小和料仓半锥角的增大主要削弱渐缩段壁面摩擦系数对卸料速率的影响程度[图7 (a)～(d)]，而料仓宽度的增加则主要削弱垂直段壁面摩擦系数对卸料速率的影响程度[图7(e)、(f)]。

图6 不同的颗粒和料仓性质下壁面摩擦系数对卸料速率的影响

图7 不同的颗粒性质和料仓性质下不同段的壁面摩擦系数对卸料速率的影响

内摩擦系数的减小增强了颗粒之间的相对滑动[33-34]。这一过程也可被认为是颗粒与壁面之间的相对滑动相对于颗粒之间的相对滑动被削弱。因此，壁面摩擦系数对卸料速率的影响程度以及卸料速率停止下降时的壁面摩擦系数的值都减小。当内摩擦系数减小为0时，在所考察的壁面摩擦系数范围内，颗粒与壁面之间的相对滑动始终比颗粒之间的相对滑动难以发生，进而使得壁面摩擦系数不对卸料速率产生影响。

随着半锥角的增大，颗粒载荷沿倾斜壁面法向方向传递的分量增大[35]，而沿其切向方向传递的分量减小。这抑制了倾斜壁面附近颗粒之间以及颗粒与壁面之间的相对滑动，进而增强了颗粒在渐缩段中流动时所受到的阻碍作用。随着渐缩段内颗粒流动的减缓，更多的上层载荷被下层颗粒支撑。这一向下传递的载荷有利于颗粒之间以及颗粒与壁面之间的相对滑动，但对前者更有利。因此，随着料仓半锥角的增大，颗粒与壁面之间的相对滑动相对于颗粒之间的相对滑动被削弱。故而，壁面摩擦系数对卸料速率的影响程度以及卸料速率停止下降时的壁面摩擦系数的值都减小。当半锥角为90°时，料仓底部形成了死区。此时，中心料仓出料口附近的颗粒在死区之间流动。卸料速率几乎完全决定于这一区域内的颗粒流动，而不受壁面摩擦系数的影响。这一结果与Anand等[10]以及Vidyapati等[9]所报道的结果一致。然而，偏心料仓出料口附近的颗粒在死区与垂直壁面之间流动。因此，其卸料速率仍受壁面摩擦系数的影响。

在窄料仓（hopper0.04 m）的渐缩段中，颗粒间的支撑作用较弱。较小的壁面摩擦系数也有利于颗粒在渐缩段的流动。因此，低壁面摩擦系数下，窄料仓中对颗粒流动的阻碍作用主要来自于颗粒在垂直段中流动时所受到的阻碍作用。增加料仓宽度可以增强渐缩段中颗粒间的支撑作用，进而增强渐缩段内对颗粒流动的阻碍作用。因此，在这一过程中，垂直段颗粒流动对卸料速率的控制作用越来越弱。故而，垂直段壁面对卸料速率的影响逐渐被削弱，并使得整个料仓的壁面摩擦系数对卸料速率的影响也被削弱。当料仓足够宽（如中心料仓宽度为0.22 m或偏心料仓宽度为0.10 m时）以使得卸料速率完全决定于渐缩段颗粒流动时，壁面摩擦系数对卸料速率的影响不再随着料仓宽度的增加而变化。此外，即使在窄料仓中，较大壁面摩擦系数下的卸料速率同样决定于渐缩段中的颗粒流动。因此，在不同宽度的料仓中，卸料速率在同一壁面摩擦系数下停止下降。

3 结 论

采用三维DEM研究了楔形中心料仓和偏心料仓中壁面摩擦系数对卸料速率的影响。这两种料仓中的卸料速率都随着壁面摩擦系数的增加而先降低后稳定。相对于中心料仓的结果，偏心料仓壁面摩擦系数对卸料速率的影响更显著，且卸料速率停止下降时的壁面摩擦系数的值也更大。随着内摩擦系数的减小和半锥角的增大，壁面摩擦系数对卸料速率的影响程度以及卸料速率停止下降时的壁面摩擦系数的值都逐渐减小。然而，增加料仓宽度仅在一定程度上削弱壁面摩擦系数对卸料速率影响程度。

壁面摩擦系数通过改变颗粒的流动行为进而影响卸料速率。壁面摩擦系数的增加抑制了颗粒与壁面之间的相对滑动，并使其最终比颗粒之间的相对滑动难以发生。内摩擦系数的减小和半锥角的增加都使得颗粒与壁面之间的相对滑动相对于颗粒之间的相对滑动被削弱。随着料仓宽度的增加，渐缩段的颗粒流动越来越强直至完全地控制卸料速率。若壁面摩擦系数的增加能够令卸料速率最终完全决定于颗粒在渐缩段的流动，则改变料仓的宽 度并不影响卸料速率停止下降时的壁面摩擦系数的值。

References

[1] Goodey R J, Brown C J, Rotter J M. Verification of a 3-dimensional model for filling pressures in square thin-walled silos [J]..., 2003, 25: 1773-1783

[2] Vidal P, Gallego E, Guaita M, Ayuga F. Finite element analysis under different boundary conditions of the filling of cylindrical steel silos having an eccentric hopper [J]...., 2008, 64: 480-492

[3] Goodey R J, Brown C J. The influence of the base boundary condition in modelling filling of a metal silo [J]..., 2004, 82: 567-579

[4] Zhu H P, Yu A B, Wu Y H. Numerical investigation of steady and unsteady state hopper flows [J].., 2006, 170: 125-134

[5] Wojcik M, Enstad G G, Jecmenica M. Numerical calculations of wall pressures and stresses in steel cylindrical silos with concentric and eccentric hoppers [J]...., 2003, 21: 247-258

[6] Ketterhagen W R, Hancock B C. Optimizing the design of eccentric feed hoppers for tablet presses using DEM [J]...., 2010, 34: 1072-1081

[7] Balevičius R, Kačianauskas R, Mroz Z, Sielamowicz I. Discrete element method applied to multiobjective optimization of discharge flow parameters in hoppers [J]...., 2006, 31: 163-175

[8] Zhu H P, Zhou Z Y, Yang R Y, Yu A B. Discrete particle simulation of particulate systems: a review of major applications and findings [J]...., 2008, 63: 5728-5770

[9] Vidyapati V, Subramaniam S. Granular flow in silo discharge: discrete element method simulations and model assessment [J]....., 2013, 52: 13171-13182

[10] Anand A, Curtis J S, Wassgren C R, Hancock B C, Ketterhagen W R. Predicting discharge dynamics from a rectangular hopper using the discrete element method (DEM) [J]...., 2008, 63: 5821-5830

[11] Nedderman R M, Tüzün U, Savage S B, Houlsby G T. The flow of granular materials (Ⅰ): Discharge rates from hoppers [J]...., 1982, 37: 1597-1609

[12] Weir G J. A mathematical model for dilating, non-cohesive granular flows in steep-walled hoppers [J]...., 2004, 59: 149-161

[13] Balevičius R, Kačianauskas R, Mróz Z, Sielamowicz I. Discrete-particle investigation of friction effect in filling and unsteady/steady discharge in three-dimensional wedge-shaped hopper [J].., 2008, 187: 159-174

[14] Langston P A, Nikitidis M S, Tüzün U, Heyes D M, Spyrou N M. Microstructural simulation and imaging of granular flows in two- and three-dimensional hoppers [J].., 1997, 94: 59-72

[15] Kruggel-Emden H, Rickelt S, Wirtz S, Scherer V. A numerical study on the sensitivity of the discrete element method for hopper discharge [J]..., 2009, 131: 031211

[16] Vivanco F, Rica S, Melo F. Dynamical arching in a two dimensional granular flow [J].., 2012, 14: 563-576

[17] Brown R L, Richards J C. Kinematics of the flow of dry powders and bulk solids [J].., 1965, 4: 153-165

[18] Laforge R M, Boruff B K. Profiling flow of particles through hopper openings [J]...., 1964, 56: 42-46

[19] Zhu H P, Yu A B. Steady-state granular flow in a 3D cylindrical hopper with flat bottom: macroscopic analysis [J]., 2005, 7: 97-107

[20] Wu Jintao (武锦涛), Chen Jizhong (陈纪忠), Yang Yongrong (阳永荣). Microscopic analysis of particle flow in moving bed [J]...:.. (浙江大学学报:工学版), 2006, 40: 864-871

[21] Wu J, Binbo J, Chen J, Yang Y. Multi-scale study of particle flow in silos [J]..., 2009, 20: 62-73

[22] Xu Y, Kafui K D, Thornton C. Silo discharge simulations with different particle properties using the distinct element method [J]..... (农业工程学报), 1999, 15: 65-69

[23] Ketterhagen W R, Curtis J S, Wassgren C R, Hancock B C. Predicting the flow mode from hoppers using the discrete element method [J].., 2009, 195: 1-10

[24] Yang S C, Hsiau S S. The simulation and experimental study of granular materials discharged from a silo with the placement of inserts [J].., 2001, 120: 244-255

[25] Balevičius R, Sielamowicz I, Mróz Z, Kačianauskas R. Investigation of wall stress and outflow rate in a flat-bottomed bin: a comparison of the DEM model results with the experimental measurements [J].., 2011, 214: 322-336

[26] Majmudar T S, Behringer R P. Contact force measurements and stress-induced anisotropy in granular materials [J]., 2005, 435: 1079-1082

[27] Delannay R, Louge M, Richard P, Taberlet N, Valance A. Towards a theoretical picture of dense granular flows down inclines [J]., 2007, 6: 99-108

[28] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies [J]., 1979, 29: 47-65

[29] Asmar B N, Langston P A, Matchett A J, Walters J K. Validation tests on a distinct element model of vibrating cohesive particle systems [J]...., 2002, 26: 785-802

[30] González-Montellano C, Ramírez Á, Gallego E, Ayuga F. Validation and experimental calibration of 3D discrete element models for the simulation of the discharge flow in silos [J]...., 2011, 66: 5116-5126

[31] Yu Y, Saxén H. Discrete element method simulation of properties of a 3D conical hopper with mono-sized spheres [J]..., 2011, 22: 324-331

[32] Masson S, Martinez J. Effect of particle mechanical properties on silo flow and stresses from distinct element simulations [J].., 2000, 109: 164-178

[33] Barreto D, O’Sullivan C. The influence of inter-particle friction and the intermediate stress ratio on soil response under generalised stress conditions [J]., 2012, 14:1-17

[34] Wang D, Zhou Y. Statistics of contact force network in dense granular matter [J]., 2010, 8: 133-140

[35] Chou C S, Chen R Y. The static and dynamic wall stresses in a circulatory two-dimensional wedge hopper [J]..., 2003, 14: 195-213

Granular discharge from concentric and eccentric wedge shaped hoppers:effect of wall friction coefficient on discharge rate

XU Pengkai, DUAN Xuezhi, QIAN Gang, ZHOU Xinggui

State Key Laboratory of Chemical EngineeringEast China University of Science and TechnologyShanghaiChina

Particle discharging from concentric and eccentric wedge shaped hoppers with different internal friction coefficients, hopper half angles and hopper widths was simulated by 3D discrete element method (DEM) and the effect of wall friction coefficient on discharging rate were investigated. In general, increasing wall friction coefficient would decrease discharging rate by retarding particle-wall slip, and the effect was more significant in wedge shaped hoppers. The friction coefficient in the convergent section had a stronger effect in reducing discharging rate than that in the vertical section. When internal friction coefficient decreased, or the width of the hopper increased, the retarding effect would decrease and eventually become insignificant.

granular flow；computer simulation；experimental validation；discharge rate；wall friction coefficient

2014-09-23.

Prof. ZHOU Xinggui, xgzhou@ecust.edu.cn

10.11949/j.issn.0438-1157.20141434

TQ 018

A

0438—1157（2015）03—0880—08

国家重点基础研究发展计划项目（2012CB720501）。

2014-09-23收到初稿，2014-11-04收到修改稿。

联系人：周兴贵。第一作者：许鹏凯（1985—），男，博士研究生。

supported by the National Basic Research Program of China (2012CB720501).