数控加工系统的可靠性分析研究与仿真

苏冬胜

（广西生态工程职业技术学院，柳州 545000）

0 引言

数控加工技术在现代工业中起着不可取代的核心地位，一旦机床的相关装置发生异常，必将影响机床的正常工作，甚至导致严重的事故，直接威胁着人们的生命财产安全[1.2]。因此，如何对数控加工系统的可靠性进行有效的检测已经成为该领域热点研究的问题之一[3]。现阶段，常用的数控加工系统可靠性检测方法主要包括基于多尺度成分分析算法的可靠性检测方法[4]、基于隐马尔科夫模型的可靠性检测方法[5]和基于数据挖掘算法的数据挖掘算法的可靠性检测方法[7]。由于对数控加工系统的可靠性分析能够实时预警数控加工系统的故障情况，为大型数控系统的维护、维修提供依据，从而保证相关设备的安全运行，因此，受到相关专家学者的重点关注，拥有十分广阔的发展前景[8～10]。

由于数控加工系统工作环境的复杂性，且受到不同运行状态的影响，其相关装置的退化程度具有较大离散性，采用传统的方法对其进行可靠性检测，往往需要耗费巨大的成本，且检测效果的精确度无法保证。

为了避免上述算法的缺陷，提出基于改进最小二乘法的数控加工系统的可靠性检测方法。依据数控加工系统可靠性的影响因素，求得不同指标的权重值，并据此制定可靠性估计参考标准，根据改进最小二乘算法原理，求解数控加工系统的故障率的加权最小二乘估计值，通过代入公式，得到可靠性估计结果，实现数控加工系统的可靠性检测。实验结果表明，采用改进算法进行数控加工系统的可靠性检测，能够有效的提高检测的准确度，节约运行成本和时间，具有更强的鲁棒性。

1 数控加工系统的可靠性检测原理

数控加工系统的可靠性即在一定条件下，在预期时间内系统保持正常工作状态的能力。数控加工系统的可靠性在很大程度上决定着数控加工系统的有效度。

设定E表示数控加工系统的有效度，F表示动力装置的工作性能，R表示装置的可靠性，A表示装置的利用率，则：

式中，F,R,A的取值区间为[0,1]，当其中任意项的因子偏向0时，则数控加工系统的有效度就会明显降低，若其中任意因子为0，则动力装置的有效度也为0。

机床的相关装置的可靠性受多种因素影响，主要可通过动力装置的零部件、装置结构及工作环境对其进行预测，其表达式可描述为：

式中， 用来描述数控加工系统的关键零部件或独立单元的可靠度，若其中任意零部件或独立单元的可靠度下降，则整个数控加工系统的可靠度也随之下降。

假设机床装置独立单元数为n，动力装置的可靠度上限值可通过下式获取：

其中，Ri表 示单元i的可靠度上限值。已知Ri= e−λit，且λi表示单元i的失效率，则：

根据已知条件，可得到数控加工系统可靠度的下限值为：

对数控加工系统可靠性的上限和下限进行综合分析，可对整个数控加工系统的可靠性进行综合预测，即：

依据上述原理可实现数控加工系统的可靠性检测，为机床相关装置的维护及维修提供可靠依据。

2 数控加工系统的可靠性检测优化算法

2.1 数控加工系统的可靠性检测标准

假设数控加工系统的可靠性是由m种因素影响，并据此将数控加工系统的可靠性分为k个等级。

式中，al用来描述指标xl与其相应的1级标准的统一度，用来描述xl与其相应的1级标准的差一级的差异度，cl用来描述xl与其相应的1级标准独立度。

由于数控加工系统受不同因素的影响程度有差异，因此，上式可转变为：

式中ωl用来描述影响设备可靠性指标xl的权重值。通过上述方法可制定数控加工系统可靠性的评测标准，为可靠性检测提供数据支持。

2.2 基于最小二乘法的数控加工系统可靠性检测方法

依据改进最小二乘法原理，数控加工系统的可靠性检测可通过下述步骤实现：

就数控加工系统某单元或零部件于某时刻发生异常的概率进行估计，表达式如下：

采用变量转换理论，将目标指数分布下的变量关系转换成线性关系；代入任意ti值到异常概率函数F(t)= 1−e−λt，即为：

则该数控加工系统的单元或者零部件的异常概率pi= F (ti),i = 1 ,2,...,m ，即：

给定yi= 1 n ( 1 − pi),i = 1 ,2,...,m ，则转换后的线性关系可描述为：

将数控加工系统的零部件的异常概率pi用其估计值替代，为减小其中的误差，可加入误差因子εi，即：

为最大化降低其中的误差值，需取下式的最小值：

对上式进行求解，得到数控加工系统零部件的异常概率估计值为：

由相关公式可获得该数控加工系统零部件发生异常的时间间隔的平均估计值，具体可描述如下：

由上可以得到指数分布下的数控加工系统的可靠性参数估计。使：

引入ni并 使加权因子ωi=，则数控加工系统的异常率最小二乘的估计值结果为：

由此获得动力装置可靠性的加权最小二乘的估计结果为：

将异常概率的估计值代入上式进行计算，即可求得数控加工系统的可靠性结果，从而实现数控加工系统的可靠性检测。

3 实验结果及分析

为了验证改进算法的有效性，需要进行实验。

实验对象选取某公司的数控机床，对象示例如下图1所示，实验中将数控加工系统的可靠性等级分为10级，最高可靠度等级为1，最低可靠度等级为0，设定50个采样点，实验过程随机选取其中的采样点进行动力装置可靠性检测实验。

图1 仿真对象示例

分别采用传统算法和改进算法进行实验，各随机选取采样点9个，得到的检测值和实际值的对比结果如图2、图3所示。

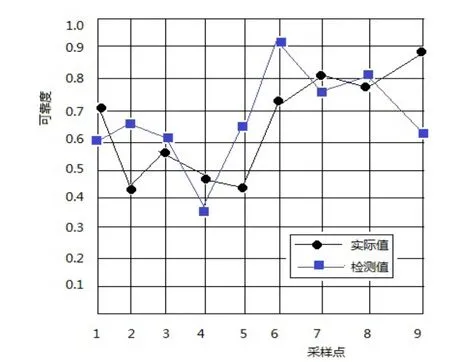
图2 传统算法检测结果

图3 改进算法检测结果

从图2、图3可以看出，利用传统算法的检测结果，可靠度值偏离实际值较大，检测结果的误差较大，利用改进算法的检测结果，则与实际值偏差较小，能够保证检测结果的准确度。

为评价不同算法的运行效率，就不同算法的收敛速度进行比较，得到的结果如图4、图5所示。

图4 传统算法的收敛速度

图5 改进算法的收敛速度

由图4、图5可以看出，采用传统算法进行数控加工系统的可靠性检测，在迭代次数为800次时，误差达到最小的状态，采用改进算法在迭代次数达到400次时即达到误差最小的状态，收敛速度明显优于传统算法，具有显著的优越性。

4 结论

数控加工系统工作环境具有复杂性，且易受到不同运行状态的影响，其动力装置的退化程度具有较大离散性，利用传统方法对其进行可靠性检测，检测准确度低，为此，提出基于改进最小二乘法的数控加工系统的可靠性检测方法。根据数控加工系统可靠性的影响因素，制定可靠性检测参考标准，依据最小二乘算法原理，获取数控加工系统可靠性的加权最小二乘估计值，得到可靠性估计结果，实现数控加工系统的可靠性检测。实验结果表明，采用改进算法进行数控加工系统的可靠性检测，可以有效的提高检测的准确性及鲁棒性，满足实际的应用需求。

[1]魏海涛.浅析电气自动化控制设备可靠性检测方法[J].商品与质量:房地产研究,2014(5):22-22.

[2]武坚,王积武,张峡辉,孙绍河,王革胜,李相全.山区村落单基站RTK测量的可靠性检测和成果精度评估[J].测绘与空间地理信息,2014,37(5):101-102.

[3]于春洪.DX-600水冷式中波发射机漏水故障检测电路原理及维护[J].电子世界,2014(19):70-71.

[4]董爱华,余琼芳.煤矿高压输电线路短路故障高可靠性检测方法[J].计算机仿真,2014,31(4):154-157.

[5]Nassim Laouti,Sami Othman,Mazen Alamir;Nida Sheibat-Othman.Combination of Model-based Observer and Support Vector Machines for Fault Detection of Wind Turbines[J].International Journal of Automation and computing,2014(3):274-287.

[6]秦凯凯.频谱分析在建筑设备电机故障检测与诊断中的应用[J].城市建筑,2014(8):205-206.

[7]张冲.电气自动化控制设备的可靠性检测基本原则和实践应用[J].电子技术与软件工程,2013(23):261-261.

[8]WEN Hao,LIN Chuang,REN FengYuan,ZHOU Jia,YUE Yao,HUANG XiaoMeng.Retransmission or redundancy:Transmission reliability study in wireless sensor networks[J].SCIENCE CHINA Information Sciences, 2012,55(4):737-746.

[9]韩静,岳江,张毅,柏连发,陈钱.光谱角匹配加权核特征空间分离变换高光谱异常检测算法[J].红外与毫米波学报,2013(4):2-8.

[10]刘辉,项昌乐,郑慕侨.模块化建模方法及其在车辆传动系中的应用[J].计算机仿真,2002,19(3):61-66.