双基地MIMO雷达发射功率聚焦的角度估计算法研究

黄中瑞 张剑云 周青松



双基地MIMO雷达发射功率聚焦的角度估计算法研究

黄中瑞*张剑云 周青松

(电子工程学院 合肥 230037)

该文针对传统双基地MIMO雷达发射功率在空间发散的问题，提出一种双基地MIMO雷达发射功率聚焦方法。首先，建立了双基地MIMO雷达发射功率聚焦的优化模型，其优化准则为：在感兴趣空域内严格约束优化波束与期望波束的最大误差小于给定门限的前提下，最小化发射方向图的峰值旁瓣功率。同时，构造特殊发射端波束矩阵，不仅能使等效发射/接收导向矢量具有旋转不变性，并且简化了原优化模型，以便采用二阶锥规划理论进行快速求解；其次，利用改进平行因子算法对空间目标的收发角度进行估计，结合发射/接收导向矢量的旋转不变性对平行因子内部最小二乘算法的初始迭代点进行了改进，有效地减小了算法的迭代步数；再次，推导了双基地MIMO雷达发射功率聚焦下多目标角度估计的克拉美罗界(CRB)，进一步说明了所提方法的优越性。最后，仿真验证了理论分析的有效性。

双基地MIMO雷达；发射功率聚焦；角度估计；改进平行因子算法；二阶锥规划；克拉美罗界

1 引言

多输入多输出(MIMO)雷达是近年来提出的一种新型体制雷达[1]。MIMO雷达的每个阵元可以独立发射波形因而具有更高的自由度[2,3]，同等阵元配置条件下与相控阵雷达相比，可以辨识更多的目标。其中双基地MIMO雷达，由于接收和发射阵列分别布置在两个相距较远的基地，因此目标具有不同的DOA和DOD，在进行检测和参数估计时，将会引入一些特殊的问题[4]，是近几年信号处理领域的研究热点。但是现有关于双基地MIMO雷达参数估计的文献，均以MIMO雷达每个阵元发射相互独立的正交波形为前提，其发射功率在空间过于发散，对于已知目标分布空域的角度估计是不利的。

文献[5]指出MIMO雷达发射方向图与其发射信号的协方差矩阵具有密切关系，文献[6,7]进一步采用不同的算法对MIMO雷达的发射方向图进行了优化。虽然文献[5-7]实现了发射功率的聚集提高了接收端的输出信噪比[8]，但是如何从具有相关性的回波中提取目标的角度信息仍是一个亟待解决的问题。文献[9]提出了一种独立于波形设计的发射方向图综合方法。将MIMO雷达的方向图综合问题转化为各个基信号线性组合系数的求解问题，从而实现方向图设计与发射波形设计的有效分离。

文献[10]在聚焦空域内对发射方向图的相位因子进行了约束使其具有近似旋转不变性，避免了文献[9]中波束矩阵对发射导向矢量造成的畸变，因而在接收端可以采用传统算法对目标角度进行估计。文献[11]对波束矩阵进行了重构，在对期望发射方向图进行较好逼近的同时，使得等效发射/接收导向矢量具有了旋转不变性，消除了文献[10]中发射导向矢量非理想旋转不变性带来的误差，进一步提高参数的估计性能。但文献[11]存在两点不足：第一，发射阵元需要基信号的个数必须为偶数；第二，接收端数据处理时，等效发射导向矢量为一个2维向量，因此严重制约了MIMO雷达的虚拟孔径扩展功能。

上述文献主要是针对单基地MIMO雷达发射功率聚焦的角度估计方法进行了研究，本文将其扩展到双基地MIMO雷达中，同时为了克服文献[10,11]在MIMO雷达发射方向图综合上的不足，给出了一种新的波束矩阵构造方法，该方法不但对基信号个数的奇偶性没有要求，而且其等效发射导向矢量维数为基信号的个数，避免了文献[11]中等效发射导向矢量维数始终为2的弊端；然后利用改进平行因子(PARAFAC)算法对目标的角度进行了估计，分析表明该算法具有较低的运算复杂度，而且能够实现收发角度的自动配对，在此基础之上推导了功率聚焦MIMO雷达目标角度估计的CRB，进一步验证了发射功率聚焦下角度估计性能的优越性。

2 MIMO雷达发射功率聚焦数学模型

考虑一双基地MIMO雷达，其发射阵列和接收阵列均为均匀线阵，阵元数分别为和，阵元间距分别为和,表示载波波长。并假设远场相同距离分辨单元内存在个目标，相对于发射阵和接收阵的角度分别为，其中，阵列配置如图1所示。

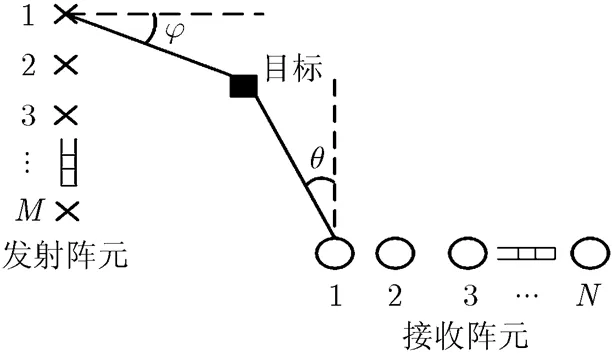
图1 双基地MIMO雷达收发阵元配置图

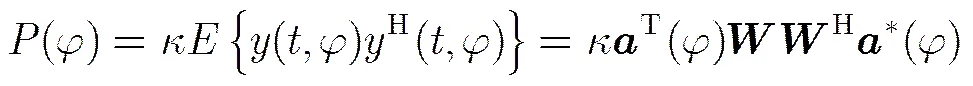
由式(1)可知，MIMO雷达发射功率的分配问题实质上就转化为如何对波束矩阵的优化问题，结合文献[10]可建立MIMO雷达发射功率聚焦的优化模型为

3 基于特殊波束矩阵构造的发射方向图优化

对于角度估计来说，波束矩阵把发射阵元的导向矢量进行了线性组合，使其不再具有旋转不变性。为避免对目标角度估计的影响，需要对波束矩阵的结构接收进行重构，以恢复等效发射导向矢量的旋转不变性。

3.1 发射功率聚焦下的接收信号模型

给出个阵元在第个脉冲时接收到个目标的回波为

用第个基信号对目标回波进行匹配滤波：

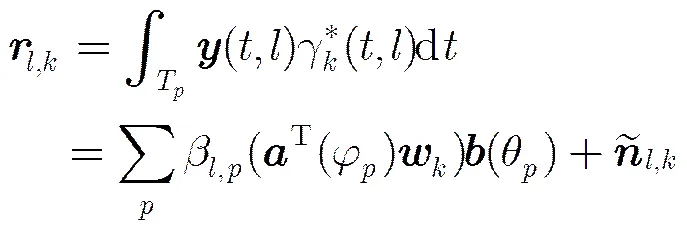
根据式(4)可得第个脉冲时刻接收阵列的匹配输出为，对其进行矩阵拉直操作得

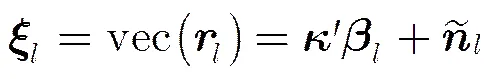
3.2 波束矩阵的构造

为了便于对目标角度进行估计，设计一个既能使MIMO雷达发射功率进行聚焦，又能使等效导向矢量具有旋转不变性的是一个亟待解决的问题。本文从波束矩阵的结构入手，在优化之前预先对其进行重构，使等效导向矢量在整个感兴趣空域均具有旋转不变性。

根据式(1)可以重新推导发射信号在空间的功率分布：

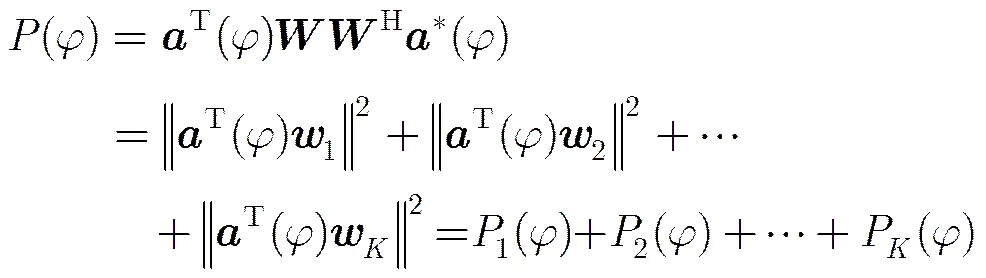
从式(6)可知，MIMO雷达发射方向图是个基信号空间分布功率的线性叠加，与的相位没有关系，所以对波束矩阵的结构进行处理，使等效发射导向矢量具有旋转不变性，不会对MIMO雷达发射方向图产生任何影响。构造的波束矩阵：

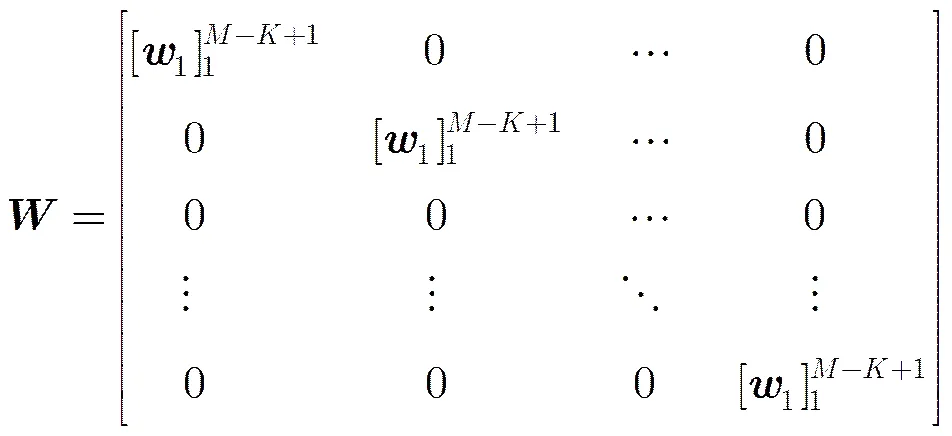
3.3 性能比较

4 发射功率聚焦的角度估计及其性能分析

4.1 基于改进PAPRFAC的角度估计

得到波束矩阵后需要根据接收信号对多个目标的收发角度进行估计，结合式(5)推得多目标情况下个回波脉冲串的匹配输出为：

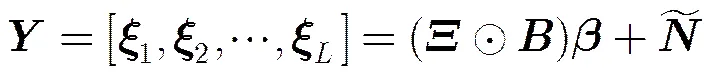
步骤3 执行以下循环体：

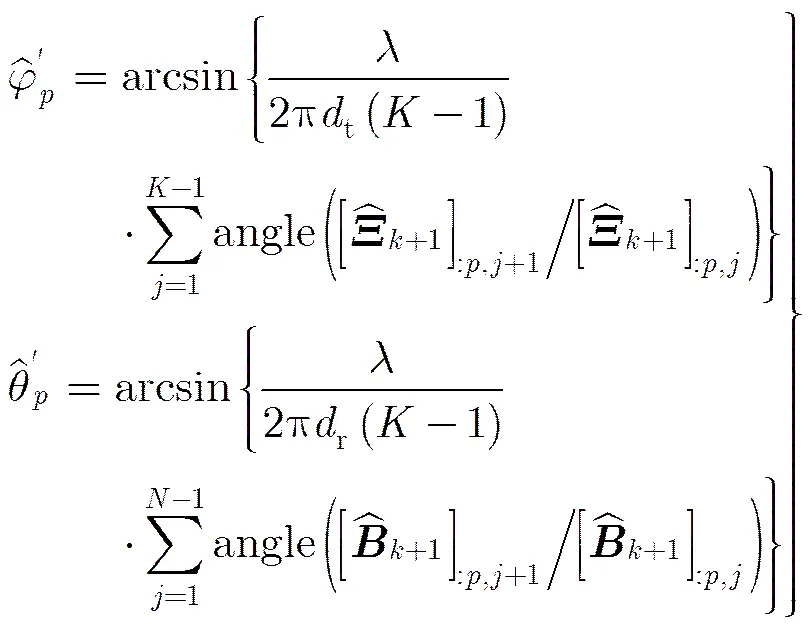
然后转入步骤3；

4.2 运算复杂度分析

采用改进PAPRFAC算法对角度进行估计，不需要进行特征值分解，TALS只需几步迭代即可收敛因而具有计算量低的特点。常规的PAPRFAC每次迭代的计算复杂度(次复乘)为，迭代过程中修正算法的计算复杂度为，因而改进PAPRFAC每次迭代的计算复杂度为，而基于ESPRIT算法的双基地MIMO雷达角度估计的计算复杂度为，相比来说本文算法的计算复杂度较低。

4.3 角度估计的CRB

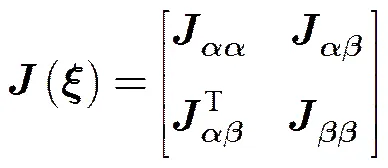
只要求得式(12)中各个分块矩阵的具体元素，并将其代入式(13)即可计算出各个目标收发角度的CRB，在求解之前首先定义,,。则的第个元素为,的第个元素为,的第个元素为，其中，

5 仿真实验

假设双基地MIMO雷达的发射阵列和接收阵列均采用线性配置，阵元间距均为半波长，发射阵元数目，接收阵元数目，发射基信号个数。分别给出如下仿真实验。

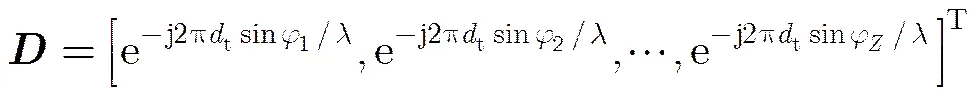
感兴趣空域内的离散化点数为100，旁瓣离散化点数为202，误差门限，对全向等功率辐射和发射功率聚焦两种情况下的发射方向图进行比较，如图2所示。

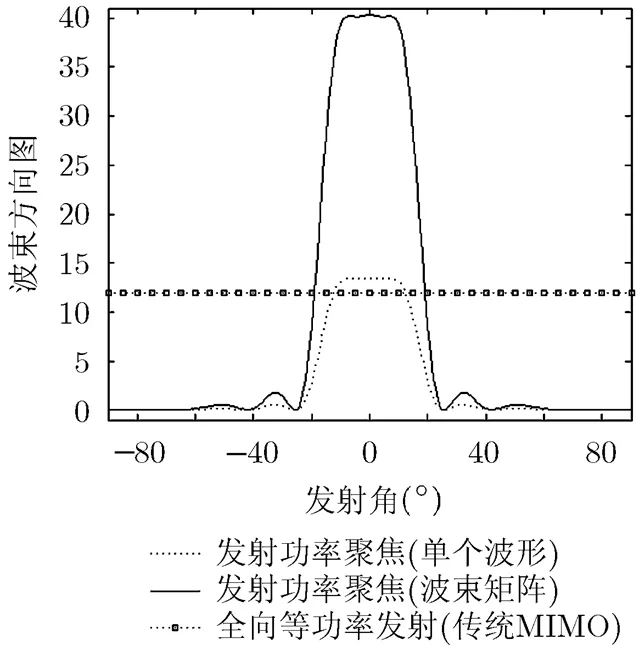
图2 两种模式下的发射方向图比较

图2给出了发射功率聚焦MIMO雷达和传统MIMO雷达的发射方向图，从中可知通过对波束矩阵进行合理的设计，可以使得MIMO雷达的发射方向图在感兴趣空域内实现能量聚焦，在不感兴趣的空域内能量最小。图2中的虚线表示一个基信号在整个空域内发射能量的分布图，其形状与发射功率聚焦MIMO雷达的发射方向图一样，只是相应位置上的能量存在整数倍(倍)的关系，这也验证了前面理论分析的正确性。图3仿真了目标分布于两个不相连的空域和的情况，从中可知，发射方向图在两个指定空域内实现了能量聚焦，且其模值增益的动态小于2，说明本文算法对于多个不相连空域内的能量聚焦也是适用的。

实验2 角度估计有效性验证 假设空中存在两个不相干目标源分布空域为，其具体角度为,，利用优化所得权值进行方向图综合，然后采用改进PAPRFAC对目标的收发角度进行估计，dB，蒙特卡洛实验次数为50，其余仿真条件同实验1。

图4和图5分别给出了功率聚焦MIMO雷达和传统MIMO雷达的目标角度估计星座图，从中可知在发射功率和估计算法一定时，功率聚焦的MIMO雷达比传统MIMO雷达具有更优的参数估计精度，在低信噪比条件下估计结果比较稳定。其原因为：实现发射功率的聚焦相当于提高了发射端的能量，因而算法一定时具有更好的角度估计效果。

图6和图7为空间两个目标收发角度估计性能随信噪比的变化图，其中仿真线上带有正方形标记的为本文方法，仿真线上带有圆圈标记的为传统MIMO雷达。从图中可知，通过对发射方向图进行预先设计可以有效提高目标处的接收能量，使输出端具有较高的信噪比(此处的信噪比与仿真条件中的信噪比不同)，因而发射功率和角度估计算法相同时，功率聚焦MIMO雷达具有更优的角度分辨率和更高的角度估计精度。

图3 多空域功率聚焦的MIMO           图4 发射功率聚焦后的目标          图5 传统MIMO雷达的目标

雷达发射方向图                      角度估计星座图                     角度估计星座图

图6 目标1收发角度估计的均方误差和成功率随SNR的变化

图7 目标2收发角度估计的均方误差和成功率随SNR的变化

6 结束语

针对传统MIMO雷达发射功率发散导致某些感兴趣空域内目标角度估计精度较差的问题，本文基于波束矩阵优化提出了一种MIMO雷达发射功率聚焦方法。通过对波束矩阵进行合理设计，可以使发射功率在感兴趣空域进行有效聚焦，从而在目标散射系数一定时使接收阵列能够获得更高的输出信噪比，构造的波束矩阵保持了收发导向矢量的旋转不变性，可以采用传统的MUSIC, ESPRIT和PAPRFAC算法对目标的收发角度进行估计；另外，在对目标的收发角度进行估计时，利用先验信息对PAPRFAC算法进行改进，可有效减小其内部交替迭代最小二乘的迭代步数；在此基础之上，推导了发射功率聚焦模式下目标收发角度估计的CRB，进一步验证了本文算法的有效性；仿真结果表明：发射功率和角度估计算法相同时，本文方法具有更优的角度估计性能。

[1] Guang H and Abeysekera S S. Receiver design for range and Doppler sidelobe suppression using MIMO and phased-array radar[J]., 2013, 61(6): 1315-1326.

[2] 杨涛, 苏涛, 张旺. 二维宽带MIMO雷达发射方向图综合方法[J]. 西安电子科技大学学报, 2013, 40(3): 180-187.

Yang Tao, Su Tao, and Zhang Wang. Transmit beampattern synthesis and waveform design for 2-D wideband MIMO radar[J]., 2013, 40(3): 180-187.

[3] Cui G L, Li H B, and Rangaswamy M. MIMO radar waveform design with constant modulus and similarity constraints[J].,2014, 62(2): 343-353.

[4] 刘晓莉, 廖桂生. 基于MUSIC和ESPRIT的双基地MIMO雷达角度估计算法[J]. 电子与信息学报, 2010, 32(9): 2179-2183.

Liu Xiao-li and Liao Gui-sheng. Combined MUSIC with ESPRIT algorithm for angle estimation in bistatic MIMO radar system[J].&, 2010, 32(9): 2179-2183.

[5] Fuhrmann D and Antonio G S. Transmit beamforming for MIMO radar systems using signal cross-correlation[J].2008, 44(1): 171-186.

[6] Shadi K and Behnia F. Transmit beampattern synthesis using eigenvalue decomposition in MIMO radar[C]. Proceedings of 8th International Conference on Information, Communications and Signal Processing, Singapore, 2011, 1-5.

[7] Lipor J, Ahmed S, and Alouini M S. Fourier-based transmit beampattern design using MIMO radar[J]., 2014, 62(9): 2226-2235.

[8] Liu J, Li H B, and Himed B. Joint optimization of transmit and receive beamforming in active arrays[J]., 2014, 21(1): 39-42.

[9] Ahmed S and Alouini M S. MIMO radar transmit beampattern design without synthesis the covariance matrix [J]., 2014, 62(9): 2278-2289.

[10] Hassanien A and Vorobyov S A. Transmit energy focusing for DOA estimation in MIMO radar with collocated antennas[J]., 2011, 59(6): 2669-2682.

[11] Ehabbazibasmenj A, Hassanien A, Vorobyov S A,. Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar[J]., 2014, 62(6): 1490-1500.

[12] Rabideau D J and Parker P. Ubiquitous MIMO multifunction digital array radar[C]. Proceedings of 37th Asilomar Conference on Signals, Systems, and Computer, Pacific Grove, CA, USA, 2003, 1: 1057-1064.

[13] Bekkerman I and Tabrikian J. Target detection and localization using MIMO radars and sonars[J]., 2006, 54(10): 3873-3883.

Study on Angle Estimation of Bistatic MIMO Radar Based on Transmit Power Focus

Huang Zhong-rui Zhang Jian-yun Zhou Qing-song

(,230037,)

In order to solve the problem that the power is transmitted dispersedly in traditional bistatic MIMO radar, a method about the transmit power focus of the bistatic MIMO radar is proposed. Firstly, the mathematic model is constructed based on an effective optimal criterion that can not only constrain the maximum error of the optimal beam and the desire one less than the given value, but also minimize the peak side lobe power of the transmit pattern. At the same time, a special beam matrix of transmitting terminal is constructed, not only making equivalent transmit/receive steering vector possessing the character of rotational invariance property, but also simplifying the original optimized model in order to be fast solved via second-order cone programming theory. Secondly, the transmitting and receiving angle of space target is estimated by utilizing improved PARallel FACtor (PARFAC) algorithm. The initial iteration point in the least square algorithm of PARFAC interior is improved by integrating into rotation invariance of transmitting/receiving steering vector, which can effectively decrease the number of iteration. Furthermore, the Cramer-Rao Bound of multi-target angle estimation under bistatic MIMO radar transmitting power focusing is derived which prove the superiority of the proposed method. Finally, the simulation results show the effectiveness of the theoretical analysis.

Bistatic MIMO radar; Transmit power focus; Angle estimation; Improving parallel factor algorithm; Second-order cone programming; Cramer-Rao Bound (CRB)

TN958

A

1009-5896(2015)10-2314-07

10.11999/JEIT150159

2015-01-27；改回日期：2015-06-16；

2015-07-27

黄中瑞 18756073857@163.com

国家自然科学基金(61201279)和安徽省自然科学基金(1408085MF128)

The National Natural Science Foundation of China (61201279); The Provincial Natural Science Foundation of Anhui (1408085MF128)

黄中瑞： 男，1988年生，博士生，研究方向为阵列信号处理、MIMO雷达信号处理.

张剑云： 男，1963年生，教授，博士生导师，主要研究方向为雷达及目标环境模拟、雷达信号处理、高速信号处理.

周青松： 男，1982年生，讲师，主要研究方向为高速数字信号处理和凸优化理论.

1)为描述方便，后文将每个发射阵元发射相互理想正交波形的MIMO雷达称为传统MIMO雷达，将本文提出的发射功率在空间能够进行聚焦的MIMO雷达称为功率聚焦MIMO雷达。