用于网络编码优化的改进量子进化算法

唐东明，卢显良



用于网络编码优化的改进量子进化算法

唐东明1，卢显良2

(1. 西南科技大学信息工程学院 四川绵阳 621010; 2. 电子科技大学计算机科学与工程学院 成都 611731)

网络编码允许网络中间节点对输入数据进行处理而非简单转发，提高了网络的吞吐量和鲁棒性，已经被证明能够达到网络最大流最小割限制。但网络节点的编码操作引发了额外的计算及资源开销。为此，该文提出了一种针对网络编码优化的改进量子进化算法IQEA-NC，以满足达到理论多播速率的情况下最小化网络的编码开销目的。IQEA-NC对传统量子进化算法进行了有效的改进，降低了算法搜索空间，增强了全局搜索能力，同时避免了陷入局部最优。仿真对比实验表明，同已有的量子进化算法及其他进化算法相比，该方法提高了优化性能，在准确性和收敛速度上都具有较大的优势。

多播; 网络编码; 优化; 量子进化算法

网络编码(network coding)[1]是一种融合编码和路由的信息交换技术，允许网络中间节点对传输的信息按照合适的方式进行编码处理而不仅仅完成存储和转发，基于该方式的网络多播能够实现最大流最小割定理确定的最大理论传输容量。文献[2]进一步证明只需要线性网络编码就可以达到网络最大传输容量。线性网络编码中，编码节点输出链接上的信息是其输入链接信息的线性组合。网络编码在提高网络吞吐量、改善负载均衡、降低无线节点能耗等方面具有明显的优势，并逐渐在内容分发[3]、分布式存储[4]、无线网络[5]、P2P网络[6]等领域得到成功应用。

然而，网络节点的编码操作引入了额外的计算开销和资源消耗，增大了系统的复杂性[7]。减少进行网络编码操作的中间节点数量具有实际的意义。事实上，编码操作不需要在所有的中间节点都实施，只要在部分节点上进行网络编码就可达到网络的最大理论传输容量[8]。然而，确定最小编码节点集被证明是一个NP难问题[8-9]。

已有的研究工作都是通过减少参与编码的中间节点数量，以降低网络编码开销，优化编码效率。文献[7]指出了针对有环和无环拓扑的网络编码节点的上界，并证明该界限仅决定于设计速率和接收节点的数量。文献[10]提出子树分解的方法，得出在双源、个接收节点的无环网络中，编码节点数不超过个。但上述两种方法依赖于信息传输的边序列，不合适的序列会导致算法性能下降并带来更多的计算开销。文献[11]提出了用于网络编码的线性规划模型，但优化算法过于复杂，随着接收节点的增加，复杂度呈指数级增长。文献[8-9]提出了基于遗传算法的网络编码优化算法，实验结果表明效果优于上述非启发式算法，但遗传算法本身存在的缺陷，如早熟、收敛速度慢等可能导致该算法表现出较差的性能。最近，量子进化算法[12]被引入到网络编码优化问题的研究中，由于该算法具有种群规模小、收敛速度快和全局寻优能力强等特点而大量应用于各种组合优化问题的求解中[13-15]。文献[16]应用量子进化算法及其改进算法解决网络编码优化问题，得到较经典遗传算法更好的性能，但该算法仅仅考虑了量子进化算法本身的性能改进，没有针对性地考虑网络编码优化问题的特殊性，当网络规模扩大时，该算法搜索能力会下降。

针对现有的网络编码优化算法存在的不足，本文以量子进化算法作为研究工具，对网络编码优化问题进行进一步的研究。提出了基于改进量子进化算法的网络编码优化算法IQEA-NC，该算法充分利用了量子计算的并行性和量子染色体多状态表征能力，同时考虑了网络编码优化的诸多约束条件，对量子进化算法进行了有针对性的改进。

1 网络编码优化问题描述

本文讨论线性网络编码下的单源多接收节点的多播问题。多播网络可以表示为一个有向无环图，其中，表示节点的集合，表示链路的集合。每个链接具有单位容量，节点间具有较大容量的链接使用多个单位容量链接表示。单源多播场景可以用一个4元组表示，即在图中，将信息从单源以速率传输到接收节点集，如果存在一种传输策略使得所有个接收节点都接收到了源节点发出的数据信息，那么称速率是可达的。

很明显，具有多个输入链接的节点才可能进行编码操作，仅一个输入链接的节点只完成信息的存储和转发。既使是多输入链接的节点，如果其输出链接的信息仅仅依赖于一个输入链接的信息，该节点仍无需进行编码操作。事实上，网络中间节点是否需要编码取决于其是否存在至少一条输出边需要传输编码信息，所以编码链接能够比编码节点更精确地表示当前网络的编码计算开销[7]。因此，本文讨论的网络编码优化问题就是在保证网络多播速率可达到的情况下，最小化参与网络编码的编码链接数量。

本文引用了代数方法[17]对网络编码优化问题进行描述。给定一个有向无环图, 如果满足条件，则称边连入边。以图为参照，生成一个有向标线图，其中，，，图中的每一条边被标记上对应的链路系数，在有限域上随机选取。按文献[17]的方法，为个接收节点中的每一个节点都建立一个的系统传递矩阵以描述源节点和每个接收节点间的关系。表示这个系统传递矩阵所对应行列式的乘积，是一个关于的多项式，当≠0时，网络可以达到给定的多播速率[17]。

2 量子进化算法

进化算法是一类模拟生物进化过程的随机搜索及优化方法，把量子计算的原理和特性融入到进化计算中产生的量子进化算法(QEA)[12]，可以充分利用量子计算的并行性和随机性解决普通进化计算在损失种群多样性时引起的早熟收敛。

2.1 量子比特

在量子进化算法中，最小的信息单元为一个量子比特(qutbit)，它的定义是在一个二维复向量空间中的一个单位向量。一个量子比特的状态可取0(记为)，或者1(记为)，或者状态0和1的不同叠加态。一个量子比特记为，可以表示为：

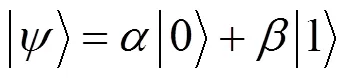
且满足归一化条件：

(2)

2.2 量子编码

量子进化算法采用了基于量子比特的编码方式，即用实数定义一个量子比特位。一个具有个量子比特位的系统可以描述为：，其中，。该表示方法可以表征任意的线性叠加态。

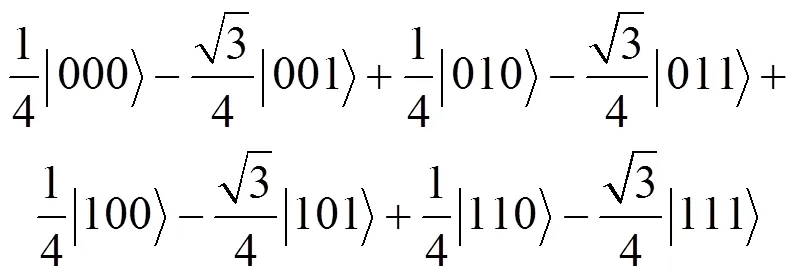
3 基于量子进化算法的网络编码优化

本文将量子进化算法用于网络编码优化问题，提出了基于改进的量子进化算法的网络编码优化算法(IQEA-NC)。针对网络编码优化问题的特点，对量子种群的初始化、观测算子及量子旋转门修正等方面进行了改进，提高量子进化算法的多样性保持能力，并降低算法搜索空间、增强全局搜索能力，同时避免陷入局部最优。

3.1 网络编码优化问题的量子比特表示

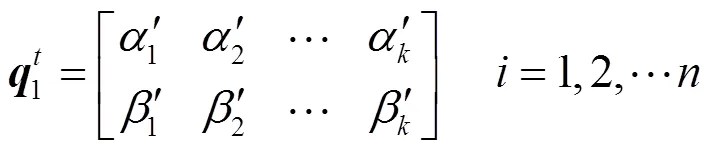
在网络编码优化问题中，本文取适应度函数为满足网络多播速率要求的前提下，参与网络编码的链接数的倒数，即：

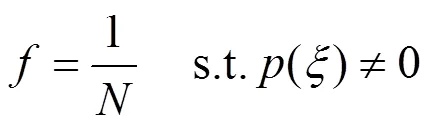
3.2 初始化种群

3.3 观测算子的改进

3.4 量子旋转门修正

量子进化算法中，采用量子旋转门操作对量子比特进行改变从而更新量子种群，促进每个量子比特的概率幅值收敛到0或者1，直到搜索到最优解。量子旋转门的定义为：

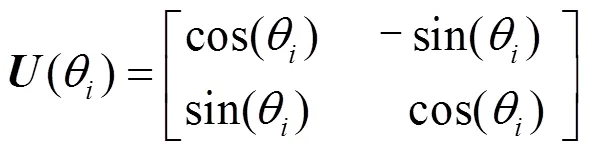
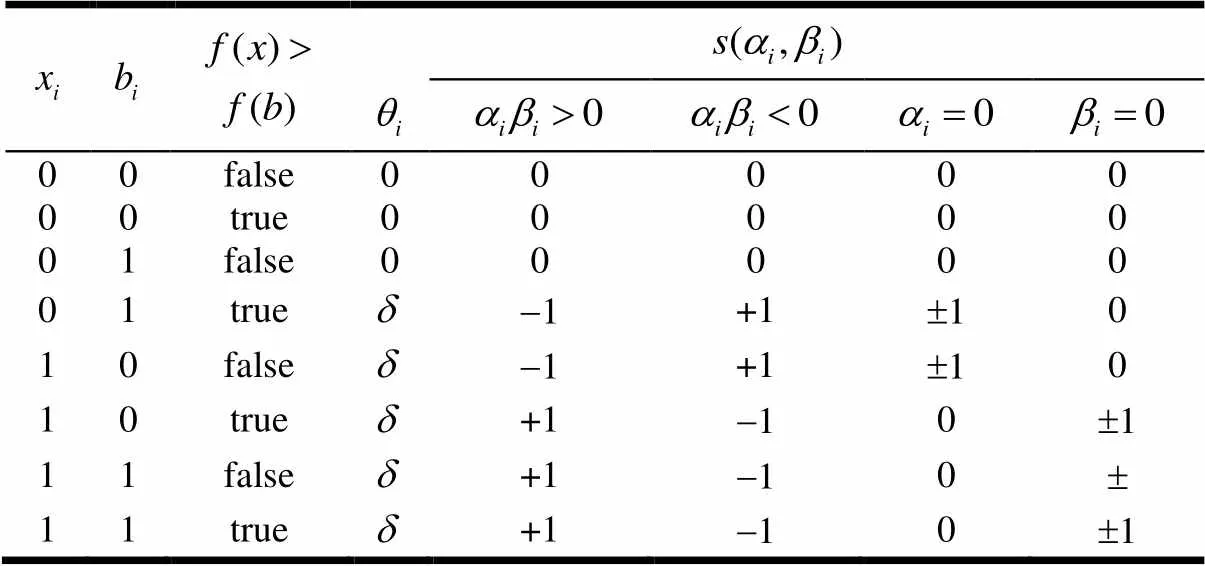
表1 量子旋转门的调整策略

量子旋转门操作定义为：

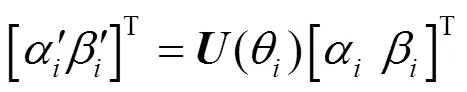
(7)

3.5 IQEA-NC算法描述

IQEA-NC算法具体步骤如下：

4) 判断终止条件是否满足，即是否满足预定义的结束条件或者最大进化代数()，若满足，则算法终止；否则，继续向下执行。

5) 根据表1查找量子旋转门的旋转角，用式(6)和式(7)对采用量子门旋转操作并进行修正，得到更新的量子种群。

4 仿真实验及结果分析

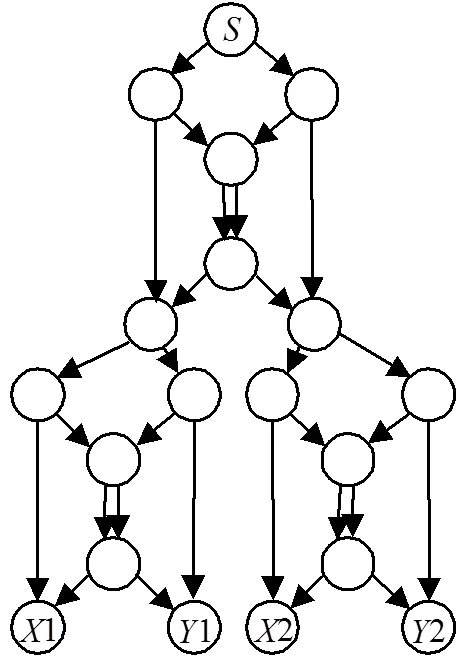
图1 人工生成的固定拓扑

为了测试和比较算法的性能，将本文算法与NCQEA[16]和SGA[8]进行性能比较，仿真在两种类型的网络拓扑结构开展，第一种是在文献[8]中使用人工生成的固定拓扑，如图1所示，记为Network 1；第二种是由BRITE模拟生成的20个节点的随机拓扑，记为Network 2，具体参数为20 nodes, 54 links, 8 sinks, rate 3。仿真实验中涉及到的算法在Matlab 7.5环境下编程实现，软件运行环境为Pentium Dual- Core CPU，2.8 GHz主频，4 GB内存。

为便于比较，3种算法设置了相同的种群大小和最大进化代数。对于IQEA-NC算法的其他参数，选取了经过多次实验尝试后的经验值，具体设置如下：种群大小，最大进化代数，量子比特概率幅值初始值，，量子旋转门的旋转角大小，门阈值，对量子种群的观测次数。

NCQEA参数设置为：种群大小为100，最大进化代数为300，初始量子旋转角度为。

SGA参数设置为：种群大小为100，最大进化代数为300，交叉概率为0.8，变异概率为0.01。

以上3种算法的终止条件为：如果连续50次相邻两代种群的最佳适应度都没有发生变化，则算法结束，否则达到最大进化代数算法结束。每种算法都运行60次，获得算法的最优值和平均值。

4.1 算法效果比较

表2给出了IQEA-NC、SGA、NCQEA在两种拓扑条件下进行60次试验后得到的编码链接数的平均结果。从测试结果看，对Network 1网络，IQEA-NC总能够得到最小的编码链接数量，同时具有较小的平均值；对Network 2网络，IQEA-NC相对于SGA，无论是最优值还是平均值，都表现出较为明显的性能优势；相对于NCQEA，两者都可以得到较小的最优值，但在平均值上，IQEA-NC比NCQEA具有更大的优势。

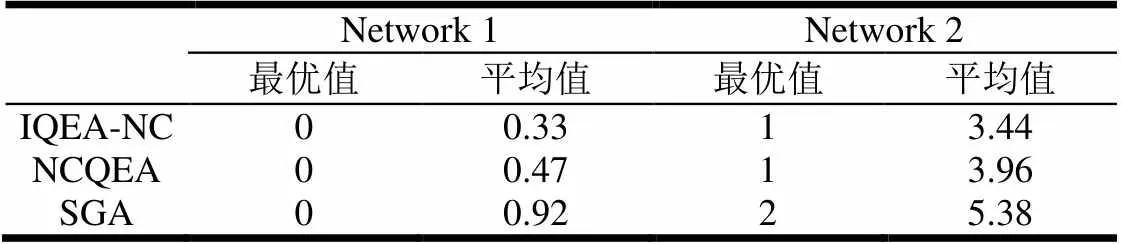
表2 IQEA-NC、SGA、NCQEA效果比较

4.2 算法收敛性比较

为比较3种算法的收敛性，本文修改了算法的终止条件，不再判断连续50次相邻两代种群的最佳适应度的变化情况，而是让算法运行到最大进化代数才结束，实验在Network 2网络上进行。图2给出了3种算法的收敛性比较。从图中可以看出，IQEA-NC的收敛速度最快，性能优于NCQEA和SGA，能够快速接近最优值；SGA进化速度缓慢，且在算法后期陷入了局部最优。另外，相对于同样基于量子进化算法的QEANC，IQEA-NC初次搜索就可以得到较优的解，这是由于采用改进的种群初始化方法，减小了算法搜索空间。采用多观测算子使算法在代内实现了局部种群优化，提高了解的质量；量子旋转门修正策略避免了算法陷入局部极值。正是这些改进，使得IQEA-NC具有更好的性能优势。

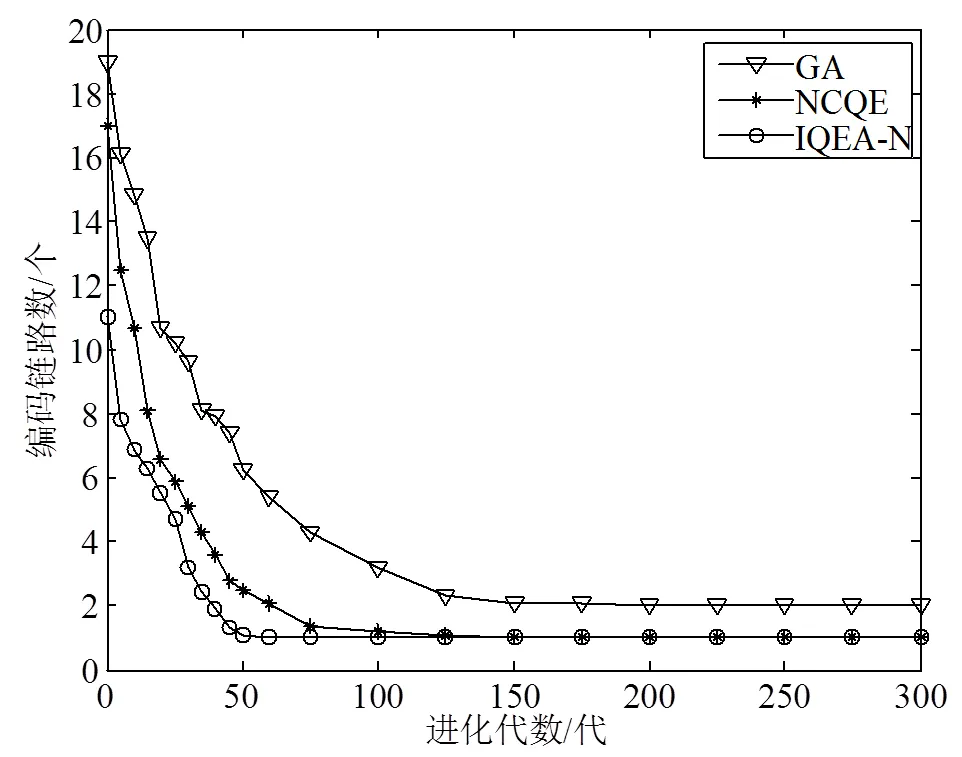
图2 算法收敛性比较

5 结 论

针对网络编码优化应用的实际特征，本文在初始种群选择、观测算子设计和量子旋转门修正策略等方面对传统量子进化算法进行了有效的改进，提出了基于改进量子进化算法的网络编码优化算法。相对于已有的基于进化算法的网络编码优化方法，本文提出的方法在满足多播速率的情况下，算法在准确性和收敛性上都有较大提高。

[1] AHLSWEDE R, CAI N, LI S Y R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216.

[2] LI S Y R, YEUNG R W, CAI N. Linear network coding[J]. IEEE Transactions on Information Theory, 2003, 49(2): 371-381.

[3] GKANTSIDIS C, RODRIGUEZ P. Network coding for large scale content distribution[C]//Proceedings of IEEE INFOCOM. Miami: IEEE Press, 2005.

[4] DIMAKIS A G, GODFREY P B, WAINWRIGHT M, et al. Network coding for distributed storage systems[C]// Proceedings of IEEE INFOCOM. Barcelona: IEEE Press, 2007.

[5] WU Y, CHOU P A, KUNG S Y. Information exchange in wireless with network coding and physical layer broadcast[C]//Proceedings of the Conference on Information Sciences and Systems, Baltimore: IEEE Press, 2005.

[6] WANG M, LI B. Network coding in live peer-to-peer streaming[J]. IEEE Transactions on Multimedia, Special Issue on Content Storage and Delivery in Peer-to-Peer Networks, 2007, 9(8): 1554-1567.

[7] LANGBERG M, SPRINTSON A, BRUCK J. The encoding complexity of network coding[C]//Proceedings of IEEE ISIT. Adelaide: IEEE Press, 2005.

[8] KIM M, AHN C W, MEDARD M. On minimizing network coding resources: An evolutionary approach[C]// Proceedings of Second Workshop on Network Coding, Theory, and Applications (NetCod2006). Boston: IEEE Press, 2006.

[9] KIM M, MEDARD M, AGGARWAL V. Evolutionary approaches to minimizing network coding resources[C]// Proceedings of IEEE INFOCOM. Baltimore: IEEE Press, 2007.

[10] FRAGOULI C, PARKER R. Information flow decomposition for network coding[J]. IEEE Transactions on Information Theory, 2006, 52(3): 829-848.

[11] BHATTAD K, RATNAKAR N, KOETTER R. Minimal network coding for multicast[C]//Proceedings of IEEE ISIT. Adelaide: IEEE Press, 2005.

[12] HAN K H, KIM J H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(6): 580-593.

[13] SILVEIRA L R, TANSCHEIT R, VELLASCO M. Quantum-inspired genetic algorithms applied to ordering combinatorial optimization problems[C]//Proceedings of IEEE World Congress on Computational Intelligence. Brisbane: IEEE Press, 2012.

[14] KIM J H, HAN J H, KIM Y H, et al. Preference-based solution selection algorithm for evolutionary multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation, 2012,16(1): 20-34.

[15] HO S L, YANG Shi-you, NI Pei-hong, et al. A quantum- inspired evolutionary algorithm for multi-objective design[J]. IEEE Transactions on Magnetics, 2013, 49(5): 1609-1612.

[16] XING Huan-lai, JIN Xing, BAI Lin, et al. A quantum- inspired evolutional algorithm for coding resource optimization based network coding multicasting [C]//Proceedings of International Conference on Semantics, Knowledge and Grid. Beijing: IEEE Press, 2008.

[17] KOETTER R, MEDARD M, An algebraic approach to network coding[J]. IEEE/ACM Transactions on Networking, 2003, 11(5): 782-795.

[18] HAN K H, KIM J H. Quantum-inspired evolutionary algorithms with a new termination criterion, H gate, and two-phase scheme[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(2): 156-169.

编 辑 税 红

Improved Quantum-Inspired Evolutionary Algorithm for Network Coding Optimization

TANG Dong-ming1and LU Xian-liang2

(1. School of Information Engineering, Southwest University of Science and Technology Mianyang Sichuan 621010;2. School of Computer Science and Engineering, University of Electronic Science and Technology of China Chengdu 611731)

It has been proved that network coding, which allows network intermediate nodes to perform processing operations on the incoming packets instead of simply forwarding them, can approach the max-flow min-cut limit of the network graph. But such coding operations in network nodes incur additional computational overhead and consume public resources. Under condition of achieving the desired throughput in multicast scenario, this paper presents an improved quantum-inspired evolutionary algorithm (IQEA-NC) to minimize network coding resources. Compared with normal quantum-inspired evolutionary algorithm, IQEA-NC can achieve some effective improvements, such as decreasing the search space, increasing global search capacity, and jumping out of local optimum. The simulation experiment results show that IQEA-NC runs faster and more efficiently, improves the optimization performance compared with the existing algorithm.

multicast; network coding; optimization; quantum-inspired evolutionary algorithm

TP393

A

10.3969/j.issn.1001-0548.2015.02.010

2013-01-11；

2014-11-04

唐东明(1974-)，男，博士生，主要从事网络信息处理、网络编码方面的研究.