基于贝叶斯组合预测方法的零售供应链协调

王文杰，刘永会

(东华大学 旭日工商管理学院，上海 200051)

基于贝叶斯组合预测方法的零售供应链协调

王文杰，刘永会

(东华大学 旭日工商管理学院，上海 200051)

运用贝叶斯组合预测方法，研究零售商和供应商协同预测条件下的需求预测问题.零售供应链协同预测需要整合供应链各方的预测方法，贝叶斯组合预测模型的构建综合了供应链各方的预测方法.运用零售业销售数据对贝叶斯组合预测模型的仿真结果表明，贝叶斯组合预测方法的预测精度优于平均组合方法和最优线性组合预测方法.

贝叶斯组合预测方法；零售供应链协调；协同预测方法；预测精度

近几年随着网络的普及，我国零售业的发展十分迅速.2012 年零售业实现增加值 1.9 万亿元，对当年 GDP 增长的贡献率为 5.9%[1]，零售供应链运营管理方面的研究备受关注.随着信息技术和网络技术的发展，零售供应链管理理念和模式得到了实质性的突破，协同计划、预测和补货(collaborative planning forecasting and replenishment,CPFR)的零售供应链协调管理模式被许多世界级的零售商和制造商采纳并实施.CPFR是针对零售业的一种供应链管理解决方案，致力于提高企业内部管理和外部协作的效率[2].其最初由VICS(the voluntary inter-industry commerce standards association)在1995年提出，它提供了零售商与供应商之间共享供应链关键信息、联合计划的框架.CPFR的实施在提高供应链运行效率的同时也提升了供应链成员之间的合作关系，为全面整合供应链奠定了基础.自1995年沃尔玛首次实施以来,CPFR已被许多国际著名企业采用，如美国的宝洁公司和欧洲的家乐福、麦德龙等.

CPFR通过使零售商和供应商共享供应商关键信息，建立联合计划的框架，然后，零售商与供应商协作生成一致的预测数据，并联合进行商品的补货.预测精度是CPFR实施成功与否的关键.预测结果偏低会导致促销期间客户的需求不能满足,从而带来销售量的损失，而预测结果过高又会产生不必要的库存，增加成本.协同预测是CPFR的核心，准确的需求预测是有效补货、有效安排生产的基础，也是降低生产、物流运输成本，增加销售额的前提[3].供应链各方预测知识和资源不同，导致各自使用的预测模型存在差异，从而产生预测异常.为解决这个问题，组合预测方法经常用于协调零售商和供应商的预测结果，提高供应链预测精度.

许多学者在组合预测方面做了大量的研究工作.文献[4]研究了减小支持向量机(SVM)中错误参数选取对预测结果的影响，提出了基于双重预测模型的非线性时间序列预测算法.文献[5]研究了数据结构突变下GM(1,1)和ARMA(auto-regressive and moving average model)的组合预测模型.多数算法都是基于数据和模型单纯地进行定量预测.而文献[6]基于贝叶斯理论分析，推导出一般条件下的非线性组合预测方法，则可以把定性与定量预测相结合.文献[7]证明了贝叶斯组合在SME(small and medium enterprises)信贷违约预判中的有效性.由于零售供应链中需求变化受产品促销、社会事件等影响较大，因此,专家经验等主观预测也是需求预测时需要考虑的重要方面，而贝叶斯组合预测方法可以集成客观和主观预测信息.因此，本文运用贝叶斯组合预测法建立零售供应链的需求预测模型.

贝叶斯原理把来自不同源的信息看作是修正先验信息的数据,从而一方面充分利用各预测方法所提供的实际信息，另一方面可考虑专家的宝贵经验、判断预测及决策者的偏好与经验，为CPFR提供协同供应商和零售商预测的有效方法.本文在组合多种单项预测方法的基础上，建立贝叶斯组合预测模型，并从多个方面验证贝叶斯组合预测方法相比于简单组合预测方法的优越性，为CPFR联合预测过程提供更有效的预测方法，以进一步提高零售业市场预测的精度.

1 模型建立

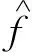
(1)

其中：φ为参数向量;YΤ=(y1,y2,…,yn)为未知量样本值.

针对(f1,f2,…,fm)单个预测的预测误差分布，引入Box-Cox变换：

(2)

设(f1,f2,…,fm)的协方差矩阵为Σ,Wi为fi的权重，令权重求解基于极小误差方差原则，则

(3)

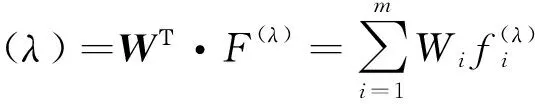
(4)

综上所述，贝叶斯分析导出如下非线性组合预测形式为

(5)

此时，最优变换参数

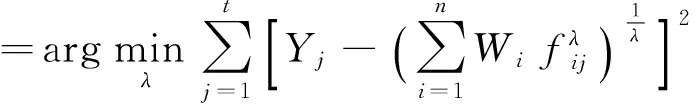
(6)

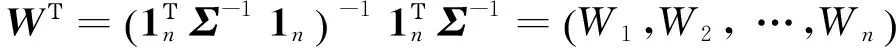
2 零售供应链协调预测仿真研究

2.1 实例数据分析

以世界著名零售商家乐福超市某种品牌饼干的销售数据为基础，表1是饼干产品39周的销售量数据.其中，第1～28周的销售数据用于拟合阶段组合预测模型的建立，第29～39周的销售数据作为对贝叶斯组合预测模型预测效果评价的对比数据.通过数据和模型的仿真研究，验证贝叶斯组合预测方法在零售供应链联合预测中的有效性和可行性.

表1 家乐福超市某类饼干销售量Table 1 Sales data of biscuit in Carrefour supermarket

在建立贝叶斯预测模型前，首先对样本数据进行检验和预处理，以去粗取精，为进一步深入分析提供较好的依据和参考.

由自相关检验(图1)可以看出，当滞后阶为1， 2， 3时，自回归值突破了可信区间的线框，说明数据在3个相邻数据内相关性较大.由偏相关检验(图2)可知，当滞后阶为1时，偏相关系数值突破了可信区间的线框，说明建立模型有1阶滞后即可.本文的销售数据是以周点为一个销售数据点的，所以可以看成滞后阶为1周.

图1 自相关检验图Fig.1 The testing for autocorrelation

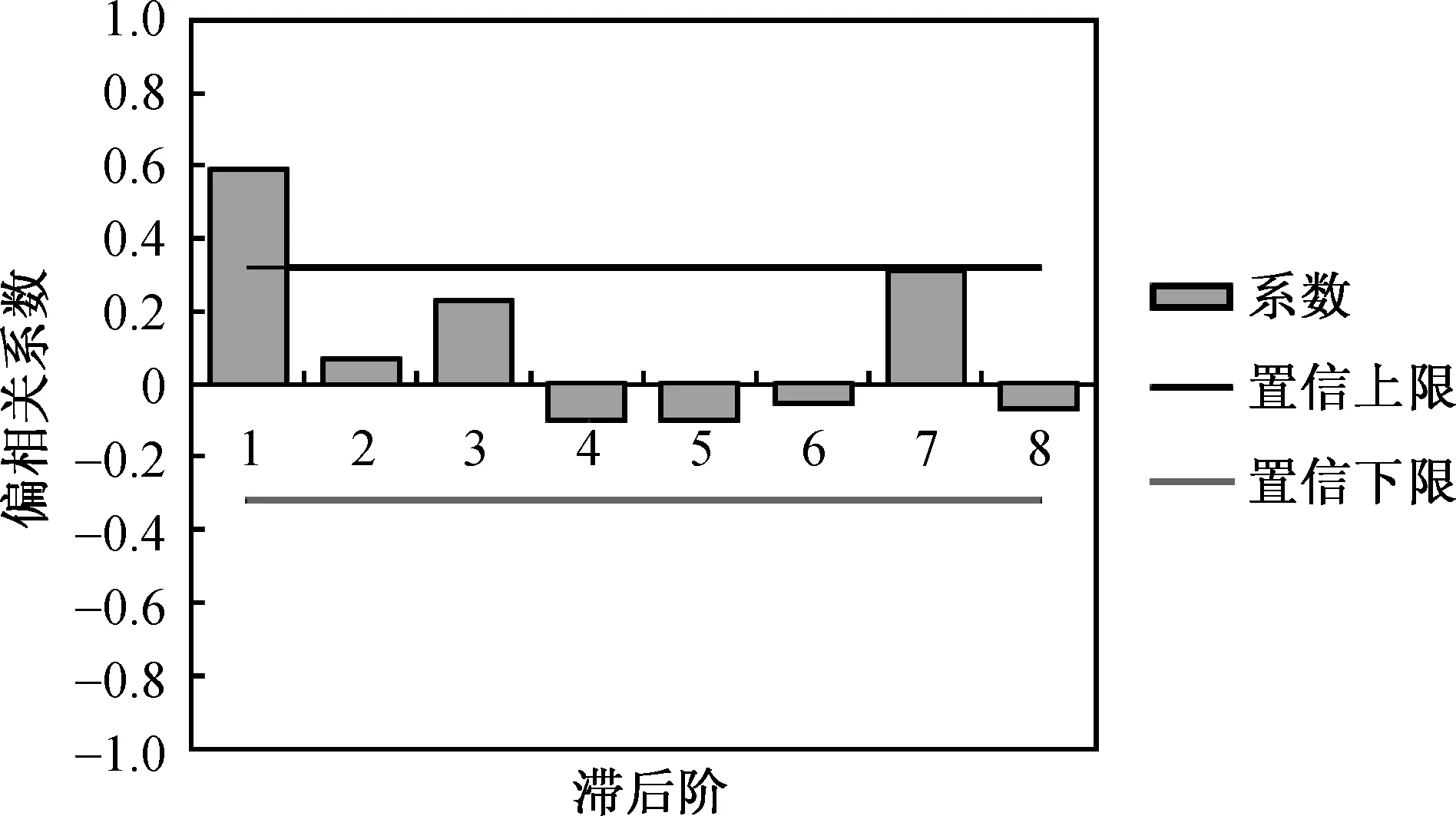
图2 偏相关检验图Fig.2 The testing for partial correlation

2.2 单项预测方法的选择

通常供应链上成员会以不同的预测方法对市场需求进行预测，从而得到不同的预测结果.本文选取移动平均法、指数平滑法、趋势外推法、ARIMA(autoregressive integrated moving average model)法、神经网络这5种预测方法，进行数据拟合和预测.在第29～39个预测周期内，各个单项预测模型的最终预测结果与真实值的比较如表2所示.其中，平均移动个数N=3时移动平均模型取得预测效果最好的预测值为F1；平滑系数a=0.6时一次指数平滑模型取得预测效果最好的预测值为F2；n=2时多项式回归模型为二次多项式回归，此时有最好预测值为F3；平稳序列阶数d=1时ARIMA模型取得最好预测值为F4； 3个神经元、2个隐含层时神经网络预测系统有最好预测值为F5.

表2 真实值与各单项预测结果汇总Table 2 The collection of real value and single forecasting data

表2给出的预测值分别为5种预测方法中的最优预测值，但是这5种预测值的组合是否最优还不能确定.由表2可知，F3明显偏离实际值，F3进入组合会影响组合的预测精度，所以剔除F3，选择F1,F2,F4,F5的预测方法进入贝叶斯组合预测模型.贝叶斯组合预测模型中的最优变换参数λ*可由式(6)求得,本文计算得λ*=7，此时预测误差平方和最小.

2.3 组合预测模型的比较

根据家乐福某种饼干第29～39周的销售量预测结果，以及移动平均模型、一次指数平滑模型、ARIMA模型和神经网络预测系统，分别建立基于平均组合方法(EV)、最优线性组合方法(MV)、加权平方和平均组合方法、加权平方根和平均组合方法、加权调和平均组合方法的组合预测模型，并使用平方和误差(SSE)、平均绝对误差(MAE)、均方误差(MSE )、平均绝对百分比误差(MAPE)、均方百分比误差(MSPE)、误差方差(S2)指标，比较这些预测模型的误差.

表3 家乐福饼干贝叶斯组合预测结果分析表Table 3 The sales forecasting data based on Bayesian combination

从表3可以看出，贝叶斯组合预测效果优于平均组合方法、最优线性组合方法等其他组合形式.这说明贝叶斯组合预测方法实现了供应链市场预测的更优协调，可以有效提高预测精度.

3 结 语

本文使用贝叶斯组合预测方法协调零售供应链各成员的预测过程，建模和仿真研究表明，贝叶斯组合预测模型实现了供应链需求预测的有效协调，其预测精度优于常用的单项预测方法，如移动平均法、指数平滑法、ARIMA模型、BP神经网络.研究结果为协调零售供应链的需求预测提供了一种新的方法，并为提高零售供应链需求预测准确度、降低供应链总成本提供了一条有效途径.

由于资料取得的限制，在模型验证方面仅采用单一产品进行试验，且影响因素牵涉不多，未来可针对更多类别的产品信息进行验证.在组合预测模型部分，由于实务资料无法完整涵盖所有的影响因素，且不同产业、产品的影响因素有所差异，后续研究可考虑针对不同产品特性发展相关协同预测模型.

[1] 中国零售业发展报告(2013)[R/OL].(2013-07-04) [2013-10-02].商务部流通发展司&中国连锁经营协会.http://www.ccfa.org.cn/viewArticle.do?id=ff8080813e9e61c3013fb88d3 de50458&method=viewArticle.

[2] LIU X H,SUN Y W. Information integration of CPFR in inbound logistics of automotive manufactures based on internet of things[J]. Journal of Computers,2012,7(2): 349-355.

[3] 隆玉玲,王文杰,方向华.CPFR组合预测方法研究[J].东华大学学报：自然科学版，2009,35(2):216-221.

[4] 方勇,刘庆山.基于双重预测模型的非线性时间序列预测[J].系统仿真技术，2011,7(2):117- 119.

[5] 杨小力,杨林岩,冯宗宪.GM(1,1)和ARMA组合预测模型及数据结构突变的预测[J].统计与决策，2006(1):4-6.

[6] 高仁祥,张世英,刘豹.组合预测贝叶斯方法研究[J].系统工程学报,1996,11(1):28-35.

[7] 高鹏,谢忠秋,王志华.基于贝叶斯组合分类的SME信贷违约预判模型[J].统计与决策，2010(18):32-35.

Study on Retail Supply Chain Coordination with Bayesian Combination Forecasting Modeling

WANGWen-jie,LIUYong-hui

(Glorious Sun School of Business and Management,Donghua University,Shanghai 200051,China)

The Bayesian combination forecast method is applied to coordinate the demand forecast between retailers and suppliers. The Bayesian combination model is created to integrate the both parties forecast methods in the retail supply chain. The simulation result show that the accuracy of Bayes combination forecast is superior to averaging combination forecasting and optimal linear combination forecasting.

Bayesian combination forecasting; retail supply chain coordination; collaborative forecasting method; accuracy of forecasting

1671-0444(2015)01-0109-04

2013-10-11

国家自然科学基金资助项目(71172174)；上海市自然科学基金资助项目(12ZR1400900)；上海市浦江人才计划资助项目(13PJC006)

王文杰(1965—)，女，江苏宜兴人，副教授，博士，研究方向为供应链管理. E-mail: wenjiew@dhu.edu.cn

F 273

A