基于分形理论的线状要素的地图自动综合算法实现
刘哲 刘潇鹏 吴洪涛
基于分形理论的线状要素的地图自动综合算法实现
刘哲 刘潇鹏 吴洪涛
(安徽理工大学测绘学院 安徽淮南 232000)
线状要素的制图综合往往由于数据容量过大在选择比例尺可视化输出时不能进行清晰图形表达。本文基于分形理论中的步距算法,在visual studio中开发系统窗口平台,以线状要素为研究对象,实现对线要素的地图自动综合计算,从而以少量控制点清晰表达出图形的轮廓特征。该方法较好的保持了地图的形状特征和细节,使化简的图形与原始数据的图形在形状结构特征上基本保持了一致性。
地图自动综合 线状要素 分形 步距法
1 引言
分形的理念最初提出来,其原义是不规则的,分数的,支离破碎的物体。人类无时无刻都在接触几何学。在历史上,科学技术的发展与几何学的进步始终是密切相关的。在生产实践和科学研究中,人们用以描述客观世界的几何学是欧几里德几何学以及解析几何、射影几何、微分几何等。但是,自然界大多数的图形都是十分复杂而且不规则的。例如:海岸线、河川、云团、闪电等等。用传统的几何学研究这一类形体是无能为力的。这时分形概念就应运而生了。粗略地说,分形是对没有特征长度但具有一定意义下的自相似性图形和结构的总称[1]。
下面给出“分形”的两个定义,在物理上易于理解,但不够精确,也不够数学化[2]。
定义1(Mandelbrot,1986),部分以某种形式与整体相似的形状叫分形。
定义2(Edgar,1990),分形集合是这样一种集合,它比传统几何学研究的所有集合还更加不规则(irregular),无论是放大还是缩小,甚至进一步缩小,这种集合的不规则性仍然是明显的。
自相似性是分形的两大基本性质之一。一个系统的自相似性是指某种结构或过程的特征从不同的空间尺度或时间尺度来看都是相似的。另外,在整体与整体之间或部分与部分之间,也会存在自相似性。一般情况下自相似性有比较复杂的表现形式,而不是局域放大一定倍数以后简单地和整体完全重合[3]。
自然界的分形,其自相似性并不是严格的,而是在统计意义下的自相似性,海岸线也是其中一个例子。凡是满足统计自相似性的分形称之为无规分形。另外,还有所谓有规分形,这类分形,由于它是按一定的数学法则呈现,因此具有严格的自相似性。
2 基于分形理论的线状要素制图综合研究
2.1 分形理论在线状要素制图综合中的算法
采用步距法对控制点进行取舍的步骤[4]:
(1)首先给定初始步长d1,并计算线符的第1点P1到第2点P2的距离d12,如果d12大于dl,则在P1与P2之间插入一点P,使P到Pl的距离为d1;如果d12小于d1,则考虑P1与P3的距离是d13,同时舍去P2;当d13大于d1时,在点P2与P3之间插入一点P,使P到Pl的距离为d1;当d13小于d1,时则再考虑d14,且跳过的P3也将舍去……,进行到线符的最后一个点后,再以P作为Pl(新出发点)重复上述过程,即可得出用d1描述线符所用的步数n1,从而得出

(2)改变步长可得到不同的线长,类似上述过程可分别得出
(2)
以此类推可以通过使用不同步长量取不同长度,可以得到不同数目的保留点。
步距法是用设定的步长通过量测线要素的每一个控制点来对控制点进行取舍,下面以线要素前三个控制点p1、p2、p3为例,构建算法流程图见图1:
2.2 基于分形理论的线状要素综合系统的设计
2.2.1 系统设计流程
系统设计的处理流程主要包括以下几个方面:
(1)根据系统建设的要求、系统功能的实现安装相应的软件。本系统需要安装:ArcGIS9.3、ArcEngine9.3、Visual Studio 2008。
(2)在Visual Studio 2008平台上主要使用MapControl、PageLayoutControl 、ToolbarControl、TOCControl等控件建立起基于分形理论的制图综合系统框架。
(3)在该系统基本框架的基础上,设计出自己想要的功能模块:获取坐标、分形演示、点线转换。
系统的基本设计流程如图2所示:
2.2.2 系统开发技术
开发语言:C#;开发环境:ArcEngine9.3、Visual Studio 2008;开发技术:VisualStudio上的窗口设计以及功能的代码实现。
2.2.3 系统开发环境的搭建
(1)安装软件
本系统的开发需要安装ArcEngine9.3、Visual Studio 2008、ArcGIS9.3。
(2)GUI设计
在Microsoft Visual Studio 2008中新建一个Visual C#下的Windows 窗口,命名为基于分形理论的制图综合系统,主要使用ArcEngine9.3下的MapControl 、PageLayoutControl 、ToolbarControl、TOCControl控件以及选择漫游、缩放、比例尺等基本控件构建系统的基本界面,如图3所示:
2.2.4 系统功能设计与实现
本系统包括五个功能模块,核心部分是输出坐标、分形演示、点转化线。
(1)文件:本菜单主要实现系统的添加数据、保存、退出三个基本功能;
GIS基本操作功能:包括数据添加、漫游、缩放、比例尺、保存等地图基本操作功能;
(2)输出坐标:实现输入原始线要素获取点坐标的txt文件;
(3)分形演示:该功能主要实现了步距法,对原要素的控制点进行取舍,将保留点的坐标txt文件输出保存并计算不同步长度量后线要素的长度;
(4)点转为线:实现了将保留点转化为线,并输出保留为shapefile文件。
2.2.5 应用实例
(1)数据准备
所用数据为具有490个控制点的长江部分数字化曲线-river.shp。
(2)输出坐标
将river.shp加载到本系统,通过输出点坐标窗口提取该线状要素的所有点控制点坐标,并输出保存为txt文件,点坐标作为分形计算(步距算法)的所用数据,如图4所示。图5是截取的部分点坐标。
(3)分形演示
将上述所得的点坐标导入分形计算窗口作为分形计算(步距算法)的操作数据,设定好步长d(以d=0.000045为例)和保留点的保存路径,点击分形计算,就能得出线要素分形后的长度和保留点的txt文件。如图6所示。
(4)点转化为线
将保留点的txt文件导入,然后设置好生成新要素的保存路径,点击生成shp就能生成保留点的shapefile文件。如图7所示。
(5) 取得成果
步距法可以删除线要素不符合条件的部分细节,完成图形的自动综合。利用本系统输入十个不同步长d得到表1,其中十个线要素长度L都保持在1.5km左右,步长d选择的越小得到的控制点越多。以d=0.000045和d=0.000065为例,当d=0.000045时分形后线要素长度L=1.504215km,保留点个数为108,舍去了382个控制点。我们将d=0.000045时线状要素化简后的新图层与原始图层相比较,可得到两者在不同比例尺下轮廓结构的变化。如图8-1和图8-2比较所示可发现两者轮廓结构上的变化,仔细观察图8-2局部放大图,很容易看出其与原图在形态结构上保持了一定的相似性。
当d=0.000065时如图8-3所示,线要素化简后的新图层与原图的相似性没有d=0.000045时保持的好。显然,步长选择的越小,两者的在不同比例尺下图层轮廓结构的相似性越大。
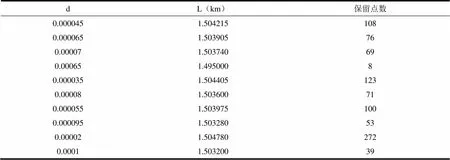
表1:10个步长所得的保留点
3 结束语
3.1 主要结论
(1)在研究线状要素制图综合的整个算法设计过程中,可以说是在理解线状要素统计性分维数定义的基础上而采取的步距法,实现它并不算困难。本文用编程语言实现步距法,运用这种分形算法可以实现对线状要素的自动综合,关键是删除那些不重要的细节。表1为分别取得十个不同步长d所得的保留点。从表1可以看出选取的d越小,保留的控制点就越多,与原图的相似性就越强,但是曲线的长度都是保持在1.5km左右。
(2)在对步长d的选取过程中,发现必须选取较小的步长才能符合线要素的标度区间。因此要想能够合适、有效地保持线符总体应有的形态结构特征,必须保留一定数量的控制点,这就需要取在标度区间内的较小步长来量测,即对步长的选取范围有一定的要求。总之该系统可以减少线要素控制点从而以少量数据表示主要的目标实体,使图层综合前后保持了图层基本的自相似性。
3.2 研究展望
(1)在研究过程中也发现研究的步距法有缺陷之处,在不同步长量测长度时并未考虑到线段特征点的取舍问题。要想保持自相似性以及转换比例尺前后的图像局部与整体都达到最大的相似,该方法只考虑到了步长改变对控制点的取舍,并未顾及到特征处控制点的保留——特征点的取舍问题,例如河流线的拐点的取舍问题没有考虑进去,因此会造成一定的变形或失真。此外,在综合过程中所用步长的选取在很大程度上是人为、主观性的,人机交互的,也会造成一定的误差。通过参阅多篇文献及数学方法的研究,觉得可采取曲率的方法先得到特征点,在保留特征点的基础上进行步长法量取取舍控制点,将会更好的的保留局部的相似性。曲率已经在很多领域用来表示线状特征,它具有旋转不变性和平移不变性的特征,而且相当稳定,与坐标系无关。通过曲率可以清楚的描述弯曲特征及方向变化,同时还能描述曲线的蜿蜒性,因此通过曲率确定曲线的形态特征。由于本人水平有限,该方法未能实现,以后有待继续研究。
(2)总体来说,基于分形理论的线状地物要素自动综合算法是一种高度自动化的地图自动综合算法,在保证图形结构特征的前提下,极大的减少了人为因素的干预。在今后的工作中,还要针对具有保留节点特征的图形化简算法进行更多的深入研究。
[1] 吴兵,葛昭攀.分形理论在地理信息科学研究中的应用[J].地理学与国土研究,2002,18(3):24-26.
[2] 周江,印萍,程荡敌等.基于GIS和分形理论研究的海岸线图像和分维以及长度[J].海洋地质与第四纪地质,2008,28(4):65-77.
[3] 姜志强.分形理论应用研究若干问题及现状与前景分析[J].吉林大学学报,2004,22(1):57-61.
[4] 何宗宜,阮依香,尹为利等.基于分形理论的水系要素制图综合研究[J].武汉大学学报,2002,27(4):427-431.

