数字无绝缘轨道电路调谐单元的谐振分析

姚向明

（北京全路通信信号研究设计院集团有限公司，北京 100073）

数字无绝缘轨道电路调谐单元的谐振分析

姚向明

（北京全路通信信号研究设计院集团有限公司，北京 100073）

介绍数字无绝缘轨道电路S型电气绝缘节的工作原理，并对调谐单元进行频率特性和特性阻抗的分析。说明数字无绝缘轨道电路的调谐单元具有良好的选频特性，并分析改变调谐单元电气参数所造成的影响。

数字无绝缘轨道电路；调谐单元；频率特性；特性阻抗

1 研究背景

随着我国经济的快速增长，城市人口迅速增加，发展速度快、运量大的城市轨道交通很自然的成了许多城市解决公共交通客运问题的首选方案，它安全、迅速、舒适、便利地在城市范围内运送乘客，最大限度地满足市民出行的需要。轨道电路作为城市轨道交通信号系统的一种模式，对保障列车的运行安全、提高列车运行效率起着非常重要的作用。

数字编码制式的无绝缘轨道电路为电气隔离式轨道电路，同一个信号点为相邻两个轨道区段的分隔点，采用调谐单元构成电气隔离，是近年来城市轨道交通轨道电路的主要形式之一。其技术先进，通用性强，电路的集成度高，软件处理能力强。本文以国产化试验型数字轨道电路为研究背景，在长春轻轨现场参数配置的基础上，通过对轨道电路调谐单元进行分析，为合理配置传输通道中器材参数提供依据，并为数轨的最大有效传输提供理论基础。

2 电气绝缘节的工作原理

在无绝缘轨道电路中，电气绝缘节有多种形式。其中，常用的主要有两种：S型绝缘节和UM71绝缘节。前者主要用在地铁、轻轨线路上，后者更多地被用在大铁线路上。S型电气绝缘节（简称S棒）的结构如图1所示。

图1 S棒的等效电路

S棒由两段钢轨和一条S型（多股铜绞线）连接线构成。图1中，支路1、2，9、10各为一段钢轨，支路3、4、5，6、7、8各为S型连接线的一部分，支路0、15分别表示本区段和邻区段轨道四端网的输入阻抗，支路11、12，13、14分别为调谐单元到S棒的引线，C16、C18为调谐电容。

S棒发送端调谐槽路主要由支路6、7、8、9、13、14的电感和支路18的电容C18构成。支路0的两端是本区段输出，支路15的两端是邻区段输出。当发送调谐槽路处于并联谐振时，S棒的输入阻抗远远高于发送器电源的内阻以及信号传输电缆的阻抗，从而使发送器输出的功率主要加在S棒上，保证本区段有较高的信号传输比。由于钢轨支路1和S棒支路7紧密接触铺设，两支路存在互感，使邻区段输出降低，保证S棒发送端有很好的隔离性能。

S棒接收端调谐槽路主要由支路2、3、4、5、11、12的电感及支路16的电容C16构成。同一区段内接收端、发送端调谐槽路的参数相同。当接收调谐槽路处于谐振时，接收端有较高的输入阻抗，保证信号的高效接收。同理，由于钢轨支路10和S棒支路4紧密接触铺设，两支路同样存在互感，使接收端邻区段输出电压降低，保证S棒接收端有很好的隔离性能。

由于引线11和引线12紧密捆绑在一起，两者间的互感应予考虑，互感会减少引线对调谐槽路的影响。同样也要考虑引线13和引线14的互感。

3 调谐单元的谐振分析

调谐单元结构和等效电路如图2、图3所示。对图3进行简化，如图4所示。

图2 调谐单元结构示意图

图3 调谐单元等效电路图

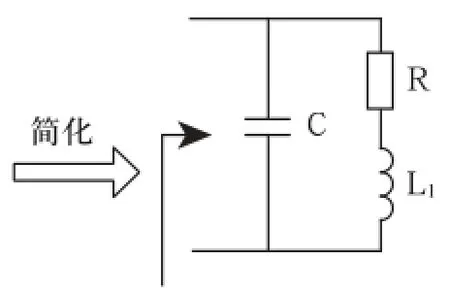
图4 简化电路图

3.1 频率特性分析

图3电路发生并联谐振，因此

可得，谐振频率：

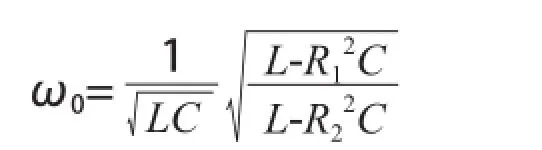
图4中，由等效变换可得

图4中的并联谐振槽路的频率特性如下：

根据上述理论公式，用matlab工具对相邻轨道电路中心频率分别为11.5 kHz和13.5 kHz的调谐单元频率特性进行模拟仿真，结果如图5所示。

数字无绝缘轨道电路正线轨道电路频率配置为 9.5、10.5、11.5、12.5、13.5、14.5、15.5、16.5 kHz，频率相差1 kHz。从图5可以看出，频率为11.5 kHz和13.5 kHz的相邻轨道电路调谐单元的带宽Bw分别为0.85 kHz和0.859 kHz，均小于1 kHz，说明该轨道电路的调谐单元具有良好的选频特性和电气绝缘性能。

3.2 特性阻抗分析

本文以本区段频率为9.5 kHz为例，由实验所测各部分参数数据带入matlab程序中，分析结果如图6所示。

在现场中，调谐单元与S棒间距离并非绝对相同，若调谐单元与S棒相距较远，钢轨接续线较长，相应的R1与L发生变化。在频率较大时，感抗的影响比电阻的影响更大。等效电路如图7所示。

图5 调谐单元频率特性（邻线频率分别为11.5 kHz和13.5 kHz）

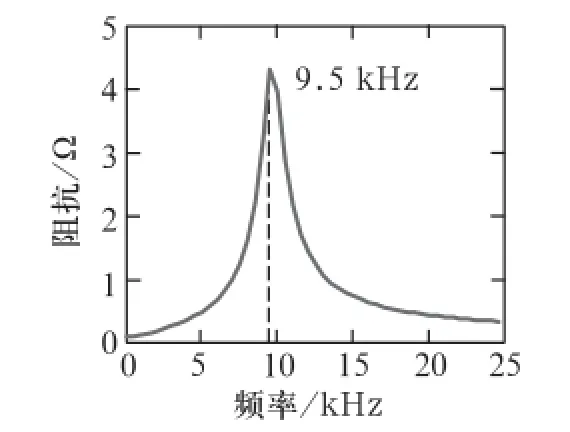
图6 阻抗-频率变化曲线图

图7 延长钢轨接续线等效电路图

此处在L处再串联一个小电感L1为1 μH模拟该情形，用matlab进行分析，阻抗随频率的变化规律如图8所示。

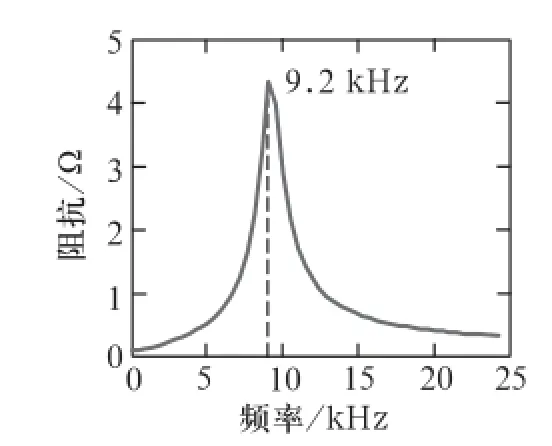
图8 延长钢轨接续线阻抗-频率变化曲线图

图8与图6比较可知，谐振点由9.5 kHz变为9.2 kHz。

在采用新调谐单元中，工艺发生变化，加长了调谐电容的引线长度。相应的R2发生变化，并有感抗出现。在频率较大时，感抗的影响比电阻的影响更大。等效电路如图9所示。

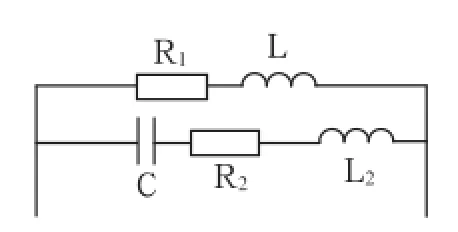
图9 延长电容引线等效电路图

此处在C的分支再串联一个小电感L2为1μH模拟该情形，用matlab进行分析，阻抗随频率的变化规律如图10所示。

从图10可知，谐振点为9.2 kHz，与加长引接线长度对调谐单元的阻抗影响类似。

图1O 延长电容引线阻抗-频率变化曲线图

由此可知，现场实际安装和工艺变化可能造成调谐单元的谐振点发生变化，因此现场安装情况改变预期时，必须进行分析验证，必要时重新设置电气参数。

4 结语

通过对数字无绝缘轨道电路的轨旁调谐单元的频率特性和特性阻抗进行分析，可以看出，数字无绝缘轨道电路具有较好的绝缘特性，相邻轨道区段相互影响较小；调谐单元的各部分参数变化均会对谐振产生影响。本文为调谐单元的谐振分析提供一种方法，对轨道电路的分析及指导轨道电路的调整具有现实意义。

［1］邹雷滨，李晓月，王厉珘.数字编码制式无绝缘轨道电路调谐单元探析［J］.城市轨道交通研究，2006，9（5）：43-45.

［2］毛广智，解学书.无绝缘轨道电路系统的图形建模［J］.计算机工程，2004，30（15）：146-148.

［3］毛广智，解学书.S型电气绝缘节的建模与分析［J］.清华大学学报（自然科学版），2004，44（10）：1364-1367.

［4］毛广智，解学书.S型电气绝缘节的建模与仿真［J］.铁道学报，2004，26（1）：45-48.

The paper introduces the principle of S-shaped electrical insulated joints in digital jointless track circuit， and analyzes the frequency characteristics and characteristic impedance of the tuning unit. It explains good frequency selecting characteristics of the tuning unit， and illustrates the impact of changing electrical parameters of the tuning unit.

digital jointless track circuit； tuning unit； frequency characteristics； characteristic impedance

10.3969/j.issn.1673-4440.2015.06.026

2013-02-04）