一种改进的组合推荐算法研究

王子政　姚卫东（北京信息控制研究所，北京　100048）

一种改进的组合推荐算法研究

王子政姚卫东
（北京信息控制研究所，北京100048）

推荐系统是解决目前信息过载问题的有效工具和方法，而在各种推荐算法中，协同过滤推荐算法的应用最为广泛。但是，基于协同过滤的推荐算法存在稀疏矩阵的问题，即：当矩阵过于稀疏时，其推荐结果误差较大。针对这一问题，提出了一种基于内容和协同过滤的组合推荐算法，并通过实验的方式与传统的协同过滤推荐算法进行了比较。实验数据表明，这种组合推荐算法具有较高的效率。

推荐系统，协同过滤，内容，组合推荐

引　言

随着互联网及信息技术的飞速发展，信息过载问题越来越突出，获取有用信息变得越来越困难。为了能够准确地找到所需的信息，人们需要付出更多的时间和精力。而推荐系统的出现，有效地缓解了这一问题。基于用户的协同过滤推荐算法在推荐系统中应用最为广泛，这种推荐算法基于用户—项目（user-item）矩阵进行计算，但是其前提是用户项目矩阵能够提供足够的信息。对于稀疏矩阵，采用这种推荐算法则会造成推荐质量下降、推荐结果误差较大等问题。

本文针对协同过滤推荐算法中存在的矩阵稀疏的问题，提出了一种基于内容和协同过滤的组合推荐算法，并将其与现有的协同过滤推荐算法进行了比较，以验证该组合推荐算法的可行性。

1　基于内容和协同过滤的组合推荐算法模型

本文将基于内容和协同过滤的组合推荐算法分为降低矩阵稀疏度模块，以及TopN邻居推荐模块等两个子模块单独进行讨论。

（1）降低矩阵稀疏度模块：为了降低矩阵的稀疏程度，合理增加用户—项目矩阵中的非零值，采用基于项目的协同过滤推荐算法，将未评价项目的评分值计算出来，填充到用户—项目矩阵中。

（2）相似邻居推荐模块：采用基于用户的协同过滤推荐算法，将用户的喜好信息预测出来，对项目的预测值进行排序，选取TopN个资源，形成推荐集合。

1.1降低矩阵稀疏度子模块算法流程设计

为了降低矩阵的稀疏度，同时增强其稠密性，直观上必须增加用户对项目的评价信息，但是在用户—项目评分矩阵中可以利用的历史信息是非常有限的。在评分矩阵中，历史数据越丰富，利用协同过滤推荐算法进行计算的结果就越精确，推荐效果也就越好。在有限的评分信息条件下，本文提出了采用基于项目的协同过滤推荐算法来增强矩阵稠密性的方法。算法过程设计如下：

输入（INPUT）：用户—项目矩阵Rm×n，待推荐项目数量NI，邻居个数N。

输出（OUTPUT）：一个稀疏程度降低的用户—项目矩阵R’m×n。

运算流程（PROCESS）：对于每个未被所有用户评价过的项目i，都执行下面的操作：（1）首先计算项目i与其它项目之间的相似度，并选出与其相似度最高的前N个项目作为其邻居项目。（2）根据项目i已经存在的用户评分信息，利用（1）中得到的N个邻居项目信息，对i中的评分信息进行计算预测。按照预测值大小进行排序，选择前NI个项目值作为其推荐评价集合。（3）将（2）中得到的项目预测值填入原用户—项目矩阵Rm×n中，形成一个新的用户—项目矩阵R’m×n。至此，完成降低矩阵稀疏程度子模块算法的设计。

1.2相似邻居推荐子模块算法流程设计

经过降低矩阵的稀疏程度处理之后，得到一个更加稠密的用户—项目矩阵R’m×n。在此之上，采用基于用户的协同过滤推荐算法，对于m个用户中的每个用户，产生其相应的推荐结果集合。算法设计如下：

输入（INPUT）：一个经过降低稀疏处理之后的矩阵R’m×n，邻居用户数量UN，推荐项目的数量IN。

输出（OUTPUT）：推荐项目的集合RS。

运算过程（PROCESS）：对于每个被推荐的目标用户u，都执行以下操作：（1）计算目标用户u与其它用户之间的相似度，并选择与其相似度最高的前UN个作为其相似邻居用户。（2）根据用户u已经存在的评价信息和（1）中得到的相似邻居用户信息，对未评价过的项目进行预测。（3）对所有未评价过的项目的预测评分值进行排序，选取评分值最高的前IN个项目进行形成用户u的推荐集合。至此，完成TopN邻居推荐子模块算法的设计。

1.3算法整体流程设计

以上对推荐算法模块的两个子模块进行了分析和设计，下面介绍组合推荐算法的整体思路和步骤。按照算法设计的总体思路及其运行步骤，从算法的输入、输出和运算流程等三个方面进行介绍。

算法具体流程如下：

输入（INPUT）：（1）用户—项目矩阵Rm×n，其中包含m个用户、n个项目，矩阵中每个元素ri， j表示用户i对项目j的评分信息；（2）用户相似性阈值Usim；（3）项目相似性阈值Isim；（4）矩阵极大稀疏度NP；（4）矩阵可计算稀疏度MP（NP>MP）；（5）邻居数目阈值NH；（6）推荐项目数量N；（7）预测评分阈值RV。

输出（OUTPUT）：RS。

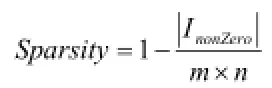
2　实验设计

2.1实验数据与评价标准

实验数据采用明尼苏达大学公开的数据集，此数据集由GroupLens项目组负责收集整理，可以从互联网站http:// grouplens.org/datasets/movielens/下载。网站中提供了不同大小的数据集合，为了实验方便，下载了100kB的数据集并进行算法的验证。在100kB的数据集合中包含943个用户、1682个项目（电影）。在不影响实验结果的前提下，为了计算方便，从全部数据集中选取78720条记录作为所有实验的数据集，其中包含400个用户和1361个项目（电影），也即在用户—项目评分矩阵Rm×n中，m=400，n=1361。矩阵Rm×n的稀疏度Sparsity=1-78720÷（400×1361）=0.8554。

在评价推荐系统的准确度时，有关文献提出，用平均绝对偏差（Mean Absolute Error，MAE）来衡量推荐系统的预测值与实际值之间的偏差。MAE是一个在统计领域经常使用的准确性评价指标，其核心思想就是计算预测值与实际值之间的偏差，偏差值越小则说明实验值与实际值之间的差距越小，也就说明实验值更加接近实际值，实验算法的效率更高。MAE的计算由下式定义：

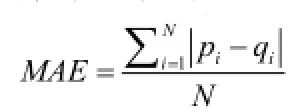
其中，pi表示预测值，qi表示实际评分值。N代表预测项目的个数。

2.2实验过程与结果分析

为了验证本文设计的组合推荐算法的推荐效果，对各种算法进行了对比。本实验中，分别对比了“改进的组合推荐算法”、“基于用户的协同过滤推荐算法”、“基于项目的协同过滤推荐算法”等三种算法的MAE值大小，以对推荐算法的有效性进行验证。为了消除稀疏程度对推荐结果的影响，本文选取实验集中75%的数据进行预测计算，剩余的25%留作与预测结果结合计算平均绝对偏差MAE。实验结果如图1所示。

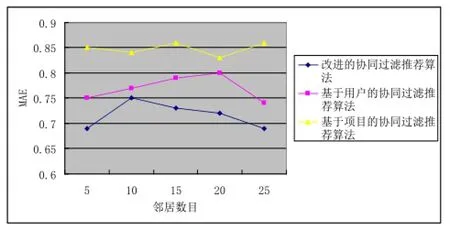
图1　改进的组合推荐算法与传统协同过滤推荐算法比对

从图1中可以看到，无论邻居数目如何变化，“改进的组合推荐算法”都较传统的协同过滤推荐算法具有更优的推荐准确度，从算法思路上来看，对于稀疏程度极大的矩阵，并不直接使用基于协同过滤的推荐算法，而是采用基于内容的推荐算法，此时由于矩阵的稀疏度较大，相应的记录较少，在使用基于内容的推荐算法时能够获得更高的推荐效率。另外，对于稀疏的矩阵，采用了基于项目的协同过滤推荐算法，首先进行了降低稀疏度处理，增强矩阵的稠密度，以便能够使用协同过滤推荐算法进行预测计算。

3　结束语

本文中提出的基于内容和协调过滤的组合推荐算法在一定程度上综合了两种算法的优点，发挥了各自的优势，降低了矩阵的稀疏程度，提高了推荐质量。与传统的、单一的推荐算法相比，该组合推荐算法的推荐质量明显提升。

1Bawden D， Holtham C， Courtney N. Courtney N. Perspectives on information overload［J］. Aslib Proceedings， 1999，51（8）: 249

2Schafer J B，Konstan J A， Riedl J. E-Commerce Recommendation Applications［J］. Data Mining and Knowledge Discovery， 2001， 5（1～2）: 115～153

3Jonathan L.， Herlocker， JosePh A， et al. Evaluating Collaborative Filtering Recommender Systems［J］. ACM Transactionson InformationSystems， 2004， 22（1）: 5～53

4张丙奇. 基于领域知识的个性化推荐算法研究［J］. 计算机工程， 2005， 31（21）: 7～9

1009-8119（2015）12（1）-0046-02