Theory of Dark Energy and Dark Matter

Marco Hernandez,Tian Ma and Shouhong Wang,∗

1Department of Mathematics,Indiana University,Bloomington,IN 47405,USA.

2Department of Mathematics,Sichuan University,Chengdu,610065,P.R.China.

Theory of Dark Energy and Dark Matter

Marco Hernandez1,Tian Ma2and Shouhong Wang1,∗

1Department of Mathematics,Indiana University,Bloomington,IN 47405,USA.

2Department of Mathematics,Sichuan University,Chengdu,610065,P.R.China.

Dedicatedto Professor Louis Nirenberg on the occasion of his 90thbirthdaywith great admiration and respect.

.In(T.Ma and S.Wang.Gravitational field equations and theory of dark matter and dark energy,Discrete and Continuous Dynamical Systems,Ser.A,34(2):335–366,2014;arXiv:1206.5078v2),a new set of gravitational field equations are derived based only on 1)the Einstein principle of general relativity,and 2)the principle of interaction dynamics,due to the the presence of dark energy and dark matter.With the field equations,we show that gravity can display both attractive and repulsive behavior,and the dark matter and dark energy are just a property of gravity caused by the nonlinear interactions of the gravitational potentialgµνand its dual field.The main objectives of this paper are two-fold.The first is to study the PID-induced cosmological model,and to show explicitly,as addressed in(T.Ma and S.Wang,Astrophysical dynamics and cosmology,Journal of Mathematical Study,47(4):305–378,2014),that 1)dark matter is due to the curvature ofspace,and 2)dark energy corresponds to the negative pressure generated by the dual gravitational potential in the field equations,and maintains the stability of geometry and large scale structure of the Universe.Second,for the gravitational field outside of a ball of centrally symmetric matter field,there exist precisely two physical parameters dictating the two-dimensional stable manifold of asymptotically flat space-time geometry,such that,as the distance to the center of the ball of the matter field increases,gravity behaves as Newtonian gravity,then additional attraction due to the curvature of space(dark matter effect),and repulsive(dark energy effect).This also clearly demonstrates that both dark matter and dark energy are just a property of gravity.

AMS subject classifications:35Q75,37N20,83C,83F

Dark matter,dark energy,principle of interaction dynamics(PID),gravitational field equations,gravitational interaction formula,stable manifold.

1 Introduction

Gravity is one of the four fundamental interactions/forces of Nature,and is certainly the first interaction/force that people studied over centuries,dating back to Aristotle,Galileo,Johannes Kepler,Isaac Newton,and Albert Einstein.It was Albert Einstein who first derived the basic law of gravity—the Einstein gravitational field equations—by postulating the principle of equivalence and the principle of general relativity.In mathematical terms,the principle of equivalence says that the space-time is a 4-dimensional Riemannian manifold{M,gµν}with metric tensor{gµν}of M being the gravitational potential.The principle of general relativity requires that the law of gravity be independent of general coordinate transformations,and dictates the Einstein-Hilbert functional.The Einstein gravitational field equations are then derived using the least action principle,also called the principle of Lagrangian dynamics.

Dark matter and dark energy phenomena are two important phenomena,which requires a more fundamental examination of the law of gravity[7–10].Recently,we have shown in[2]that the presence of dark matter and dark energy implies that the variation of the Einstein-Hilbert functional must be taken under energy-momentum conservation constraint,and we call such variation the principle of interaction dynamics(PID).With PID,we have derived the new gravitational field equations:

supplemented by the energy-momentum conservation:

Hereφis a scalar field defined onM,and needs to be solved together with the Riemannian metricgµν,representing the gravitational potential.Also ∇µis the gradient operator onM,RµνandRare the Ricci and scalar curvatures,andTµνis the energy-momentum of the baryonic matter in the universe.

With the new gravitational field equations,we have shown in[2]that gravity can display both attractive and repulsive effect,caused by the duality between theattractinggravitational field{gµν}and therepulsivedual vector field{Φµ},togetherwith their nonlinear interactions governed by the field equations.Consequently,dark energy and dark matter phenomena are simply a property of gravity.

The main objective of this article is to further explore the nature of dark matter and dark energy,in connection with

1)the geometric structure of our Universe derived in[1],and

2)the gravitational force formula and large distance asymptotic flatness of gravity in a central gravitational field.

We proceed as follows.

First,we have shown in[1]a new cosmology theorem that our Universe is a three dimensional sphere and is static,assuming the Einstein general relativity and the cosmological principle that our Universe is homogeneous and isotropic.By using the new gravitational field equations applied to homogeneous spherical universe,we explicitly demonstrate that 1)dark matter is caused by the space curvature,and 2)dark energy represents the negative pressure in the PID cosmological model:

caused by the dual gravitational field Φµ=∇µϕin the new gravitational field equations.HereRis the cosmic radius.

Second,consider a central gravitational field generated by a ballBr0with radiusr0and massM.It is known that the metric of the central field atr＞r0can be written in the form

andu=u(r),v=v(r).Then the fields equations(1.1)take the form

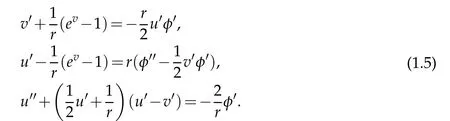
We have derived in[2]an approximate gravitational force formula

demonstrating the presence of both dark matter and dark energy.

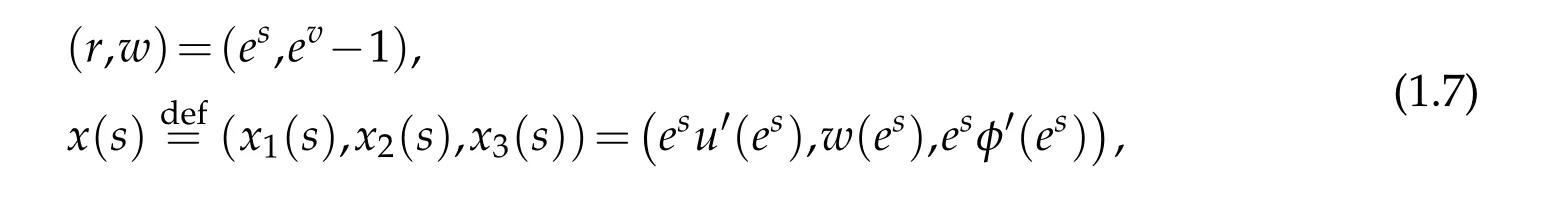
Third,we discover in this paper that under the following transformation thenon-autonomousgravitational field equations(1.5)are amazingly becoming anautonomous system:

Then we rigorously show the following conclusions:

1)The asymptotically flat space-time geometry is represented byx=0,which is a fixed point of the system(1.8a).There is a two-dimensional stable manifoldEsnearx=0,and consequently there are exactly two free parameters,to be determined by experiments(or by astronomical measurements),which give rise to asymptotical lf atness atr=∞.

2)The gravitational forceFinduced by the centrally symmetric matter is given by(4.5),and is asymptotically zero as the distance tends to infinity.

3)For the initial date near the Schwarzschild solution(4.7)satisfied by all physically meaningful central fields,there exists a sufficiently larger1such that the gravitational forceFis repulsive forr＞r1.

These asymptotic properties of gravity,displaying the key features of dark energy,plays the role to stabilize the large scale homogeneous structure of the Universe.

The paper is organized as follows.Section 2 recalls the dark energy and dark matter phenomena.Section 3 explores the nature of dark energy using the PID-induced cosmological model.Section 4 recalls the gravitational force formula deduced in[2].In Section 5,we study the asymptotic flatness and rigorously prove the existence ofdark energy at large distance outside of a spherically symmetric matter field.Section 6 addresses the two physical parameters in the gravitational interaction formula,and Section 7 addresses the nature of dark energy and dark matter.

2 Dark energy and dark matter phenomena

Dark matter and Rubin rotational curve.In astrophysics,dark matter is an unknown form of matter,which appears only participating in gravitational interaction,but does not emit nor absorb electromagnetic radiations.

Dark matter was first postulated in 1932 by Holland astronomer Jan Oort,who noted that the orbital velocities of stars in the Milky Way don’t match their measured masses.Namely,the orbital velocityvand the gravity should satisfy the equilibrium relation

whereMris the total mass in the ballBrwith radiusr.But the observed massM0was less than the theoretic massMrin(2.1),and the differenceMr−M0was explained as the presence of dark matter.The phenomenon was also discovered by Fritz Zwicky in 1933 for the missing mass in the orbital velocities of galaxies in clusters.Subsequently,other observations have manifested the existence of dark matter in the Universe,including the rotational velocities of galaxies,gravitational lensing,and the temperature distribution of hot gaseous.

A strong support to the existence of dark matter is the Rubin rotational curves for galactic rotational velocity.The rotational curve of a galaxy is the rotational velocity of visible stars or gases in the galaxy on their radial distance from the center of the galaxy.The Rubin rotational curve amounts to saying that most stars in spiral galaxies orbit at roughly the same speed.If a galaxy had a mass distribution as the observed distribution of visible astronomical objects,the rotational velocity would decrease at large distances.Hence,the Rubin curve demonstrates the existence of additional gravitational effect to the gravity by the visible matter in the galaxy.

More precisely,the orbital velocityv(r)of the stars located at radiusrfrom the center of galaxies is almost a constant:

as illustrated typically by Figure 2.1(a),where the vertical axis represents the velocity(Km/s),and the horizontal axis is the distance from the galaxy center(extending to the galaxy radius).However,the calculation from(2.1)gives a theoretic curve as shown in Figure f6.15(b),showing discrepancies between the mass determined from the gravitational effect and the mass calculated from the visible matter.The missing mass suggests the presence of dark matter in the Universe.

In fact,we have seen in[1,4]that the dark matter is a space curved energy,or equivalently a gravitational effect,which is also reflected in the revised gravitational force formula in which there is an additional attracting force to the classical Newtonian gravity.

Dark energy.Dark energy was first proposed in 1990’s,which was based on the hypotheses that the Universe is expanding.

The High-zSupernova Search Team in 1998 and the Supernova Cosmology Project in 1999 published their precisely measured data of the distances of supernovas and the redshifts.The observations indicated that the measured and theoretical data have a deviation,which was explained,based on the Hubble Law and the Friedmann model,as the acceleration of the expanding universe.The accelerating expansion is widely accepted as an evidence of the existence of dark energy.

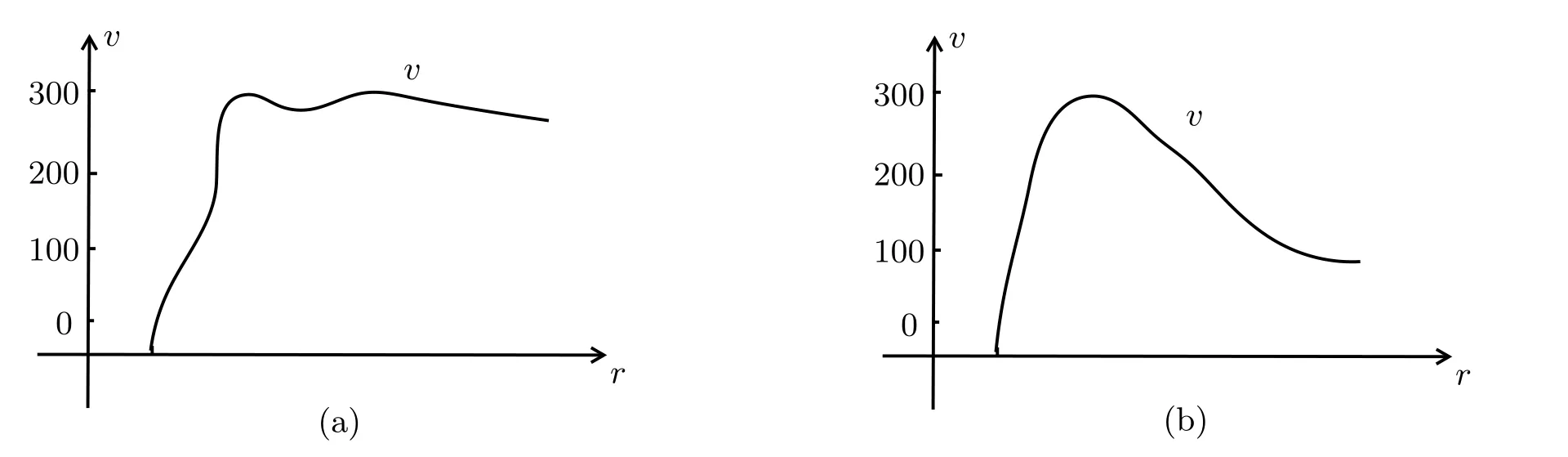
Figure 2.1:(a)Typical galactic rotational curve by Rubin,and(b)theoretic curve based on the Newtonian gravitational law.

However,based on the new cosmology postulated in the last section,the dark energy is a field energy form of gravitation which balances the gravitational attraction to maintain the homogeneity and stability of the Universe.

3 PID cosmological model and dark energy

We have shown in[2]that both dark matter and dark energy are a property of gravity.Dark matter and dark energy are reflected in a)the large scale space curved structure of the Universe caused by gravity,and b)the gravitational attracting and repelling aspects of gravity.In this section,we mainly explore the nature of dark energy in aspect a)using the PID-induced cosmological model.This section was deduced in[3,Section 7.6.2].

PID cosmological model

The metric of a homogeneous spherical universe is of the form

whereR=R(t)is the cosmic radius.The PID induced gravitational field equations are given by

where Φ=gαβDαβφ,andφdepends only ont.

The nonzero components ofRµνread as and byTµν=diag(c2ρ,g11p,g22p,g33p),we have

Thus,we derive from(3.2)two independent field equations as

We infer from(3.3)and(3.4)that

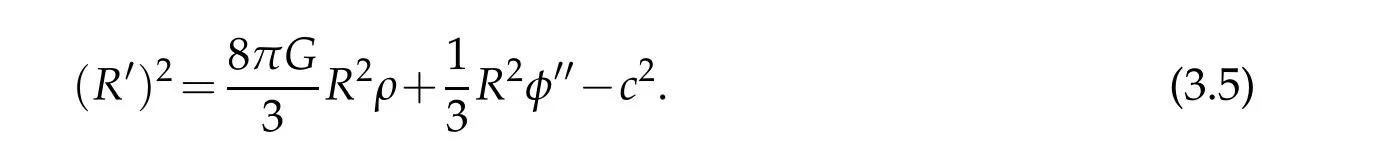
By the Bianchi identity:

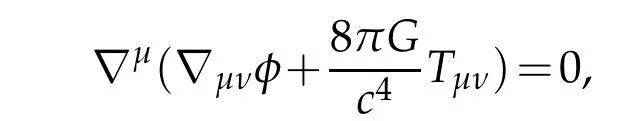
we deduce that

It is known that the energy densityρand the cosmic radiusR(also called the scale factor)satisfy the relation:

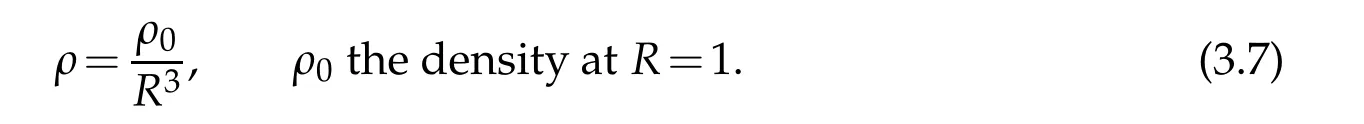
Hence,it follows from(3.7)that

Thus,(3.6)is rewritten as

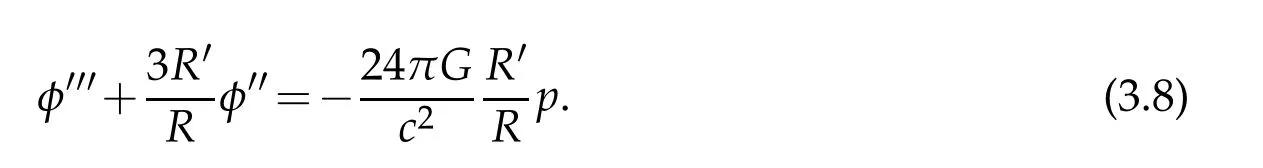
In addition,making the transformation

then,from(3.3),(3.5)and(3.7)-(3.9)we can deduce that

Denoteϕ=φ′′,by(3.10),Eqs.(3.3),(3.5)and(3.8)can be rewritten in the form

Only two equations in(3.11a)are independent.However,there are three unknown functionsR,ϕ,pin(3.11a).Hence,we need to add an additional equation,the equation of state,as follows:

Based on[1,Theorem 6.2],the model describing the static Universe is the equation(3.12)together with the stationary equations of(3.11a),which are equivalent to the form

The equations(3.12)and(3.13)provide a theoretic basis for the static Universe,including the dark energy.

Now,we need to determine the explicit expression for the equation(3.12)of state.It is natural to postulate that the equation of state is linear.Hence,(3.12)can be written as

whereα1andα2are nondimensional parameter,which will be determined by the observed data.

The equations(3.13)and(3.14)are the PID cosmological model,where the cosmological significants ofR,p,ϕ,ρare as follows:

whereMandMtotalare the observed and total mass respectively;see also[1,Remark 6.1].

Here,we remark that in the classical Einstein field equations whereφ=0,the relation(3.7)still holds true,by which we deduce thatR′·p=0.

Theory of dark energy

In the static cosmology,dark energy is defined in the following manner.LetEobbe the observed energy,andRbe the cosmic radius.We define the observable mass and the total mass as follows:

IfMT＞Mob,then the difference

is called the dark energy.

The CMB measurement and the WMAP analysis indicate that the difference∆Ein(3.18)is positive,

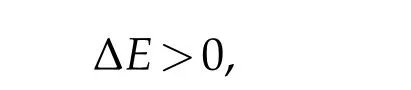
which is considered as another evidence for the presence of dark energy.

From the PID cosmological model(3.13)-(3.15),we see that the dark energy∆Ein(3.18)is essentially due to the dual gravitational potentialϕ.In fact,we infer from(3.13)that

Hence,dark energy is generated by the dual gravitational field.This fact is reflected in the PID gravitational force formula derived in sections hereafter.

If we can measure precisely,with astronomical observations,the energy(3.16)and the cosmic radiusR(i.e.MTof(3.17)),then we can obtain a relation between the parametersα1andα2in(3.14).In fact,we deduce from(3.13)and(3.14)that

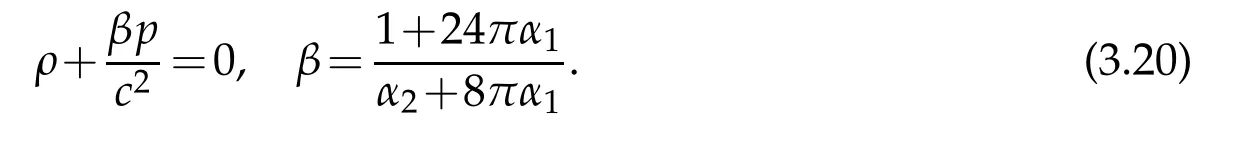
As we get

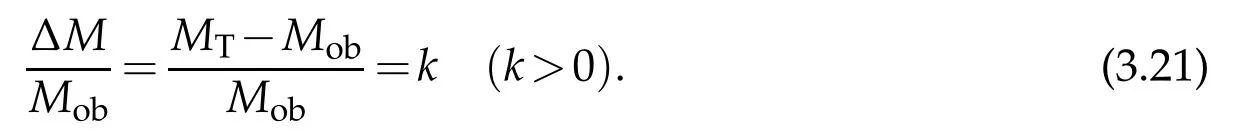
Then by(3.20)and

we obtain from(3.20)that

By the relation(3.22)from(3.20),we can also derive,in the same fashion as above,the dark energy formula(3.21).

4 PID gravitational interaction formula

Consider a central gravitational field generated by a ballBr0with radiusr0and massM.It is known that the metric of the central field atr＞r0can be written in the form

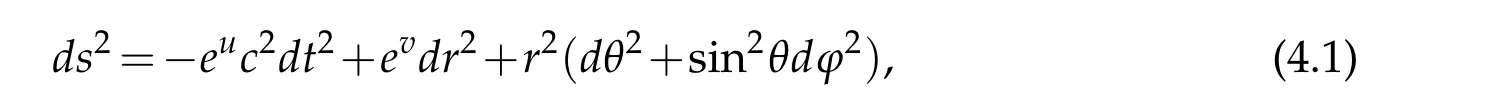
andu=u(r),v=v(r).

In the exterior ofBr0,the energy-momentum is zero,i.e.

Hence,the PID gravitational field equation for the metric(4.1)is given by

whereφ=φ(r)is a scalar function ofr.

As in[2],we have

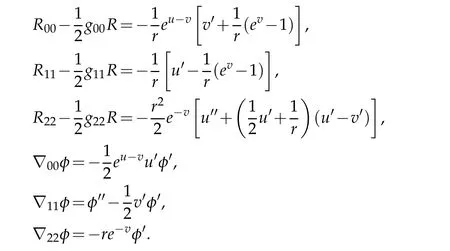
Thus,the fields equations(4.2)are as follows

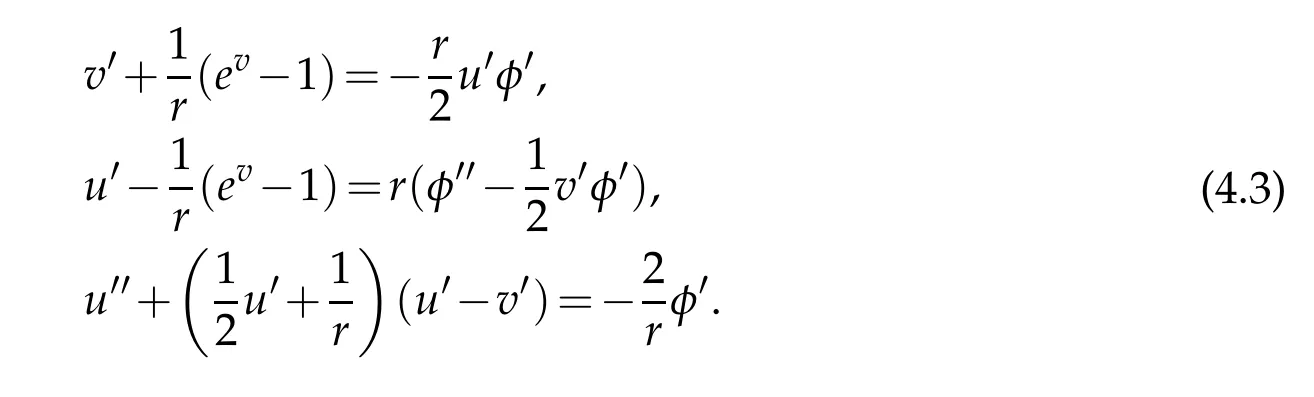
Now we are ready to deduce from(4.3)the PID gravitational interaction formula as follows.First,we infer from(4.3)that

Consequently,

It is known that the interaction forceFis given by

Then,it follows from(4.4)that

The formula(4.5)provides the precise gravitational interaction force exerted on an object with massmin a spherically symmetric gravitation field.

In classical physics,the field functionsuandvin(4.5)are taken by the Schwarzschild solution:

andφ′=φ′′=0,which leads to the Newton gravitation.

However,due to the presence of dark matter and dark energy,the field functionsu,v,φin(4.5)should be an approximation of the Schwarzschild solution(4.6).Hence we have

Under the condition(4.7),formula(4.5)can be approximatively expressed as

5 Asymptotic repulsion of gravity

In this section,we shall consider the asymptotic properties of gravity,and rigorously prove that the interaction force given by(4.8)is repulsive at very large distance.

To this end,we need to make the following transformation to convert the field equations(4.3)into a first order autonomous system:

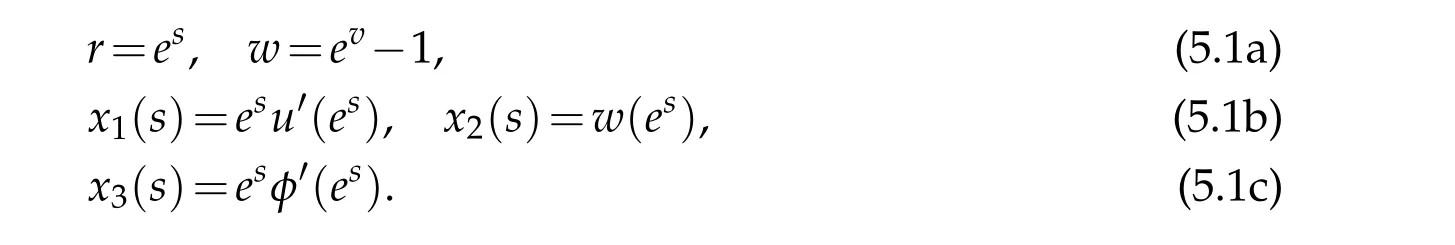
Then the equations(4.3)can be rewritten as

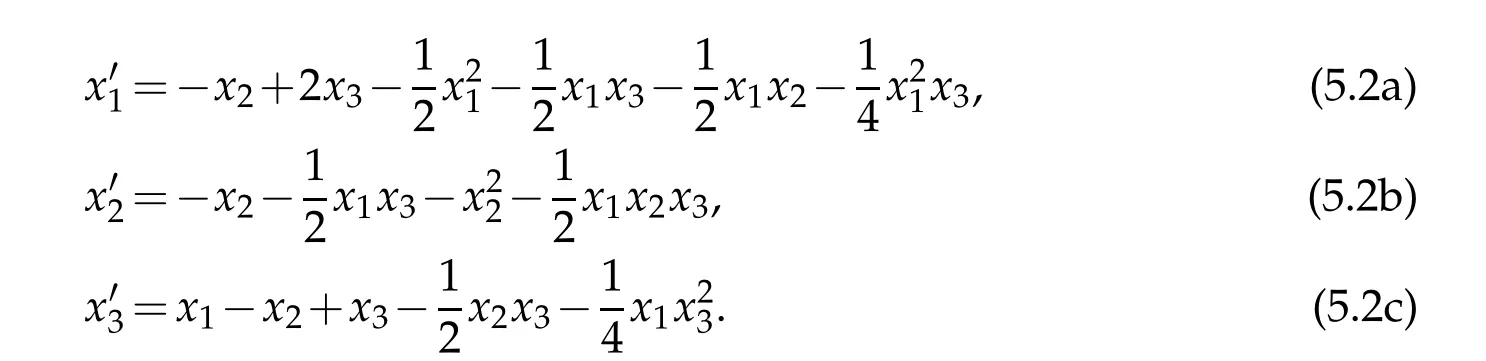
The system(5.2)is supplemented with an initial condition

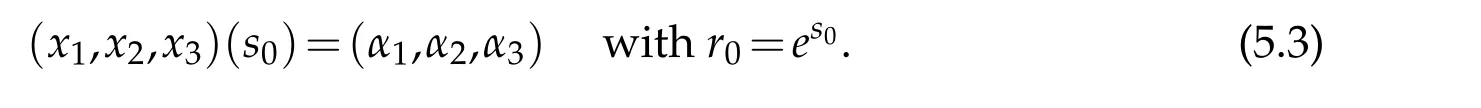
We now study the problem(5.2)-(5.3)in a few steps as follows.

Step 1.Asymptotic flatness.For a globular matter distribution,its gravitational field should be asymptotically flat,i.e.

It implies thatx=0 is the uniquely physical equilibrium point of(5.2)and the following holds true:

Step 2.Physical initial values.The physically meaningful initial valuesα=(α1,α2,α3)in(5.3)have to satisfy the following two conditions:

(a)The solutionsx(s,α)of(5.2)-(5.3)are asymptotically flatin the sense of(5.4).Namely,

the initial valuesαare in the stable manifoldEsofx=0,defined by

(b)The solutionsx(s,α)are near the Schwarzschild solution:

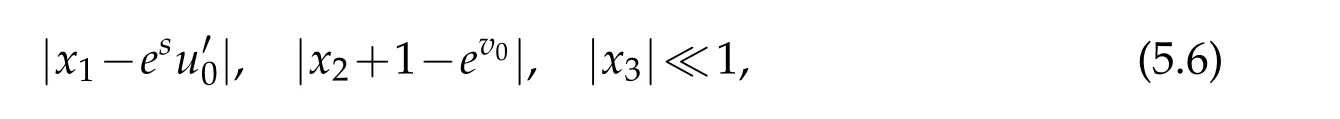
whereu0,v0are as in(4.7).

In fact,by(4.7)and(5.1a)we can see that all Schwarzschild solutions lie on the line

In particular,the lineLis on the stable manifoldEsof(5.5).

Step 3.Stable manifold Es.The equations(5.2)can be written as

The dimension of the stable manifoldEsis the number of negative eigenvalues of the matrixA.It is easy to see that the eigenvalues ofAare given by

Hence,the dimension ofEsis two:

Consequently,the initial valueαof an asymptotically flat solution has only two independent components due toα∈Es,which is of two dimensional.Namely,we arrive at the following conclusion.

Physical Conclusion 5.1.In the gravitation formula(4.5)there are two free parameters to be determined by experiments(or by astronomical measurements).

In fact,the two free parameters will be determined by the Rubin rotational curve and the repulsive property of gravity at large distance.

Step 4.Local expression of Es.In order to derive the asymptotic property of the gravitational forceFof(4.5),we need to derive the local expression of the stable manifoldEsnearx=0.Since the tangent space ofEsatx=0 is spanned by the two eigenvectors(1,1,0)tand(1,−1,−1)tcorresponding to the two negative eigenvaluesλ1=λ2=−1,the coordinate vector(0,0,1)ofx3is not contained inEs.This implies that the stable manifold can be expressed nearx=0 in the form

Inserting the Taylor expansion for(5.9)into(5.2),and comparing the coefficients,we derive the following local expression of(5.9)of the stable manifold function:

Inserting(5.9)-(5.10)into the first two equations of(5.2),we deduce that

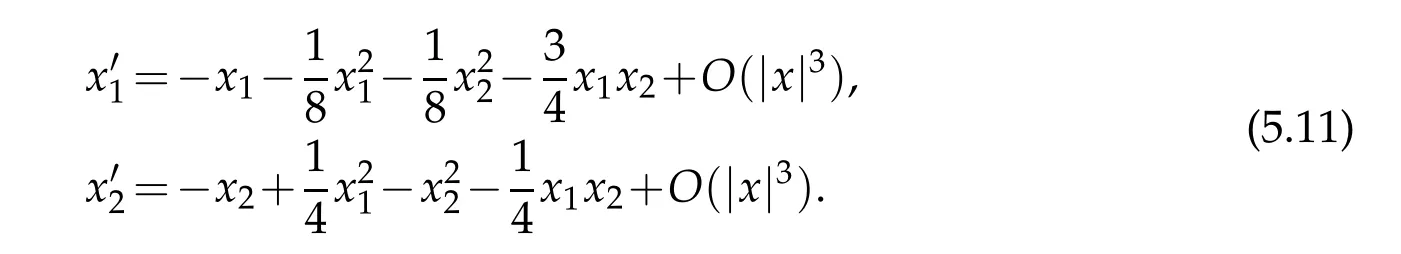
The system(5.11)is the system(5.2)restricted on the stable manifoldEs.Hence,its asymptotic behavior represents that of the interaction forceFin(4.5).

Step 5.Phase diagram of system(5.11).In order to obtain the phase diagram of(5.11)nearx=0,we consider the ratio:x′2/x′1=dx2/dx1.Omitting the termsO(|x|3),we infer from(5.11)that

Letkbe the slope of an orbit reaching tox=0:

Then(5.12)can be expressed as

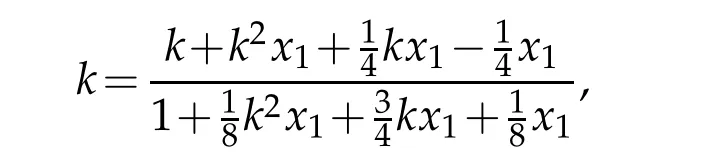
which leads to the equation

This equation has three solutions:

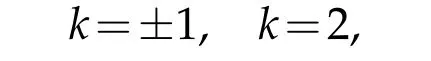
giving rise to three line orbits:

which divide the neighborhood ofx=0 into six invariant regions.It is clear that all physically meaningful orbits can only be in the following three regions:

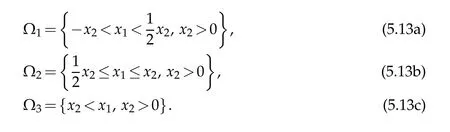
On the positivex2-axis(i.e.x1=0,x2＞0),which lies in Ω1,Eqs.(5.11)take the form

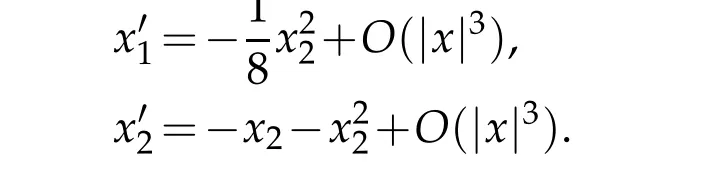
It is easy to show that the orbits in Ω1withx1＞0 will eventually cross thex2−axis.Thus,using the three invariant sets in(5.13a),we obtain the phase diagram of(5.11)onx2＞0 as shown in Figure 5.1.In this diagram,we see that,the orbits in Ω2and Ω3will not cross thex2-axis,but these in Ω1withx1＞0 will do.

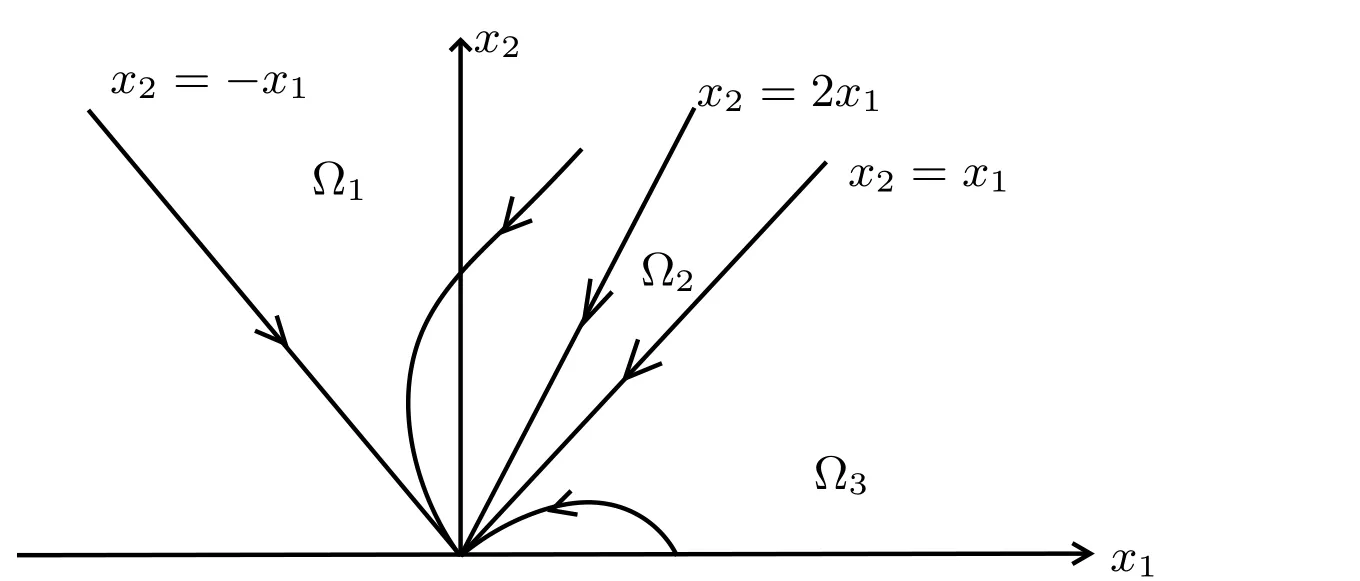
Figure 5.1:Only the orbits on Ω1 with x1 ＞0 will eventually cross the x2-axis,leading to the sign change of x1,and to a repelling gravitational force corresponding to dark energy.

Step 6.Asymptotic repulsion theorem of gravity.We now derive an asymptotic repulsion theorem of gravity,based on the phase diagram in Figure 5.1.In fact,by(4.4)and(4.5),the gravitational forceFreads as

It is known that

Hence,byx1=ru′(r)and(5.14),the phase diagram shows that an orbit in Ω1,starting withx1＞0,will cross thex2-axis,and the sign ofx1changes from positive to negative,leading consequently to a repulsive gravitational forceF.Namely,we have obtained the following theorem.

Theorem 5.1.Asymptotic Repulsion of Gravitation For a central gravitational field,the following assertions hold true:

1)The gravitational force F is given by(4.5),and is asymptotic zero:

2)If the initial value α in(5.3)is near the Schwarzschild solution(4.7)with0＜α1＜α2/2,then there exists a sufficiently large r1such that the gravitational force F is repulsive for r＞r1:

We remark that Theorem 5.1 is valid provided the initial valueαis small because the diagram given by Figure 5.1 is in a neighborhood ofx=0.However,all physically meaningful central fields satisfy the condition(note that any a black hole is enclosed by a huge quantity of matter with radiusr＞0≫2MG/c2).In fact,the Schwarzschild initial values are as

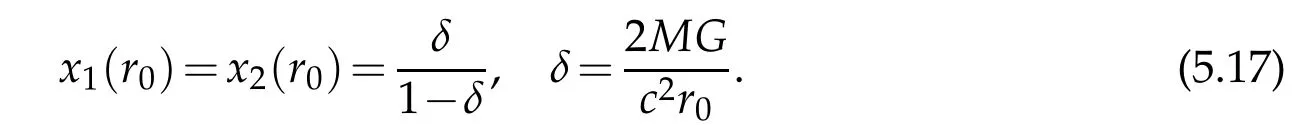
For example see(4.5),where theδ-factors are of the orderδ≤ 10−1,sufficient for the requirements of Theorem 5.1.

The most important cases are forgalaxies and clusters of galaxies.Forthese two types of astronomical objects,we have

Thus theδ-factors are

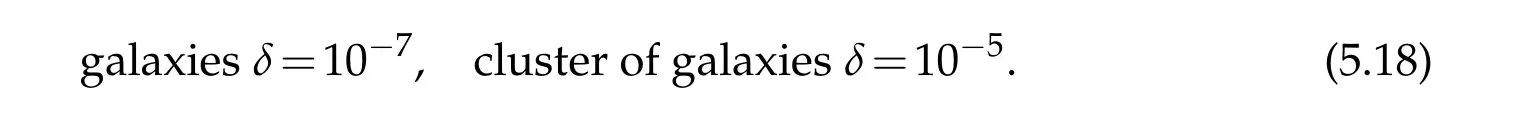
In fact,the dark energy phenomenon is mainly evident between galaxies and between clusters of galaxies.Hence,(5.18)shows that Theorem 5.1 is valid for both central gravitational fields of galaxies and clusters of galaxies.The asymptotic repulsion of gravity plays the role to stabilize the large scale homogeneous structure of the Universe.

6 Simplified gravitational interaction formula

We have shown that all four fundamental interactions are layered.Namely,each interaction has distinct attracting and repelling behaviors in different scales and levels.The dark matter and dark energy represent the layered property of gravity.

In this section,we simplify the gravitational formula(4.8)to clearly exhibitthe layered phenomena of gravity.

In(4.8)the field functionsuandvcan be approximatively replaced by the Schwarzschild solution(4.6).Since 2MG/c2ris very small forr＞r0as indicted in(4.5)and(5.18),the formula(4.8)can be expressed as

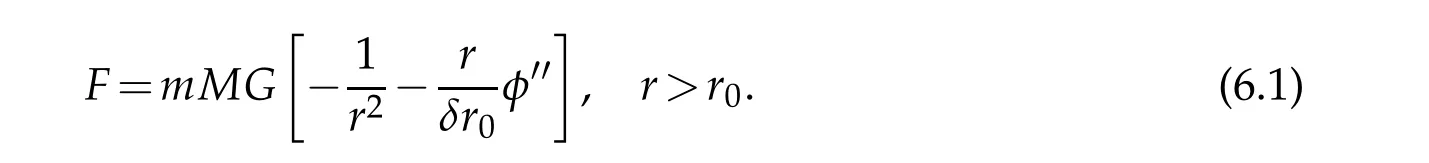
By the field equation(4.2),we have

whereRis the scalar curvature,and

In view of(6.2),we obtain that

Again by the Schwarzschild approximation,we have

Integrating(6.3)and omittinge±δr0/r,we derive that

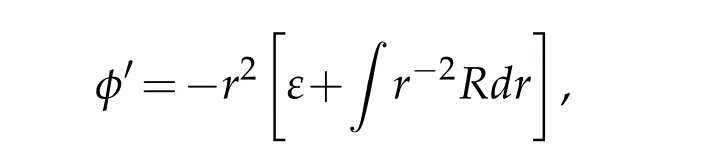
whereεis a constant.Thus(6.1)can be rewritten as

The solutions of(5.2)can be Taylor expanded.Hence by(5.1a)we see that

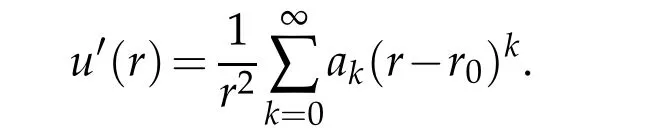
By(5.14),the gravitational forceFtakes the following form

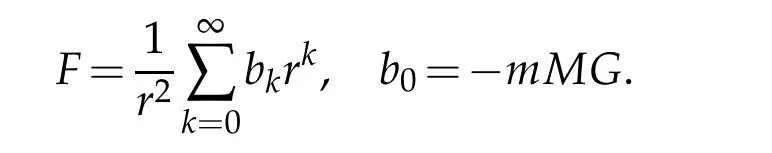
In view of(6.4),it implies thatRcan be expanded as

and by Physical Conclusion 5.1,ε0andε1are two to-be-determined free parameters.InsertingRinto(6.4)we obtain that

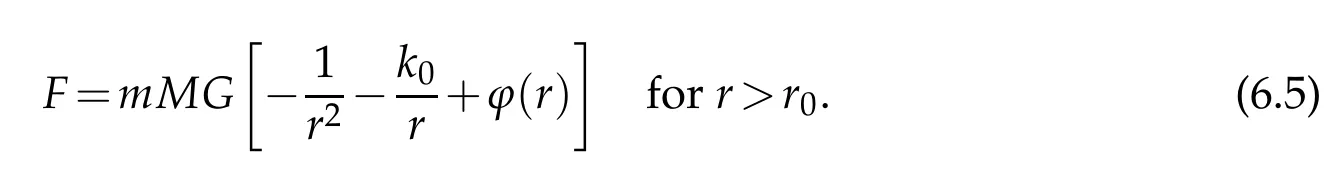
wherek0=12ε0,and

The nature of dark matter and dark energy suggests that

Based on Theorem 5.1,ϕ(r)→0 asr→∞,and(6.5)can be further simplified as in the form forr0＜r＜r1,

wherek0andk1will be determined by the Rubin rotational curve and the astronomical data for clusters of galaxies in the next section,where we obtain that

The formula(6.6)is valid only in the interval

andr1is the distance at whichFchanges its sign:

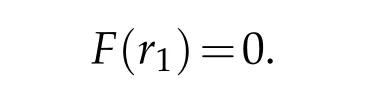
Both observational evidence on dark energy and Theorem 5.1 show that the distancer1exists.The formula(6.6)with(6.7)clearly displays the layered property of gravity:attracting at short distance and repelling at large distance.

7 Nature of dark matter and dark energy

As mentioned in Section 3,both dark matter and dark energy are a property of gravitational effect,reflected in two aspects,which will be addressed in detail in this section:

a)spatially geometrical structure,and

b)gravitational attracting and repelling as in(6.6).

Space curved energy and negative pressure

Gravitational potential causes space curvature and the spherical structure of the Universe,and displays two types of energies:a)dark matter contributed by the curvature of space,and b)dark energy generated by the dual gravitational potential in(3.15).We address each type of energy as follows.

1)Dark matter:the space curved energy.In[1,Section 6.3],we have introduced the space curved energyMtotalfor the 3D spherical Universe as follows:

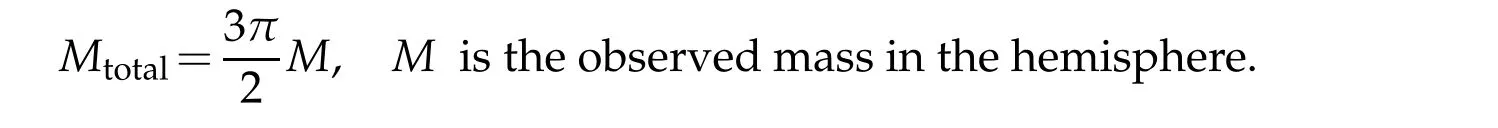
Now,we considera galaxy with an observed massMΩ.In[1,Section 6.3],we have shown that the space curved energyMtotal;Ωis

where Ω is the domain occupied by the galaxy,VΩand|Ω|are the volumes of curved and flat Ω.VΩcontain two parts:

It is known that

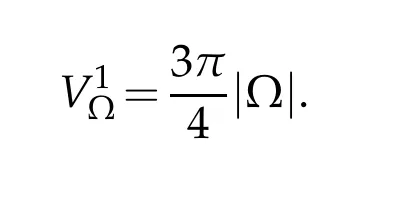
ForV2Ω,we propose that

In fact,the formula is precise for the galaxy nucleus.

By|Ω|=43πr30,we infer from(7.1)and(7.2)that

which gives rise to the relation between the masses of dark matter and observable matter.

2)Dark energy:the dual gravitational potential.The static universe is described by the stationary solution of(3.11a)-(3.12),which is given by(3.13)-(3.14).In the solution a negative pressure presents,which preventsgalaxies and clusters ofgalaxies from gravitational contraction to form a void universe,and maintains the homogeneous distribution of the Universe.The negative pressure contains two parts:

where the first term is contributed by the observable energy,and the second term is the dark energy generated by the dual gravitational potentialϕ;see also(3.19).

By the Blackhole Theorem,[1,Theorem 4.1],black holes are incompressible in their interiors.Hence,in(7.4)the negative pressure

is essentially the incompressible pressure of the black hole generated by the normal energy.

By the cosmology theorem,[1,Theorem 6.2],the Universe is a 3Dsphere with a blackhole radius.However,theCMBand theWMAPmeasurements manifest that the cosmic radiusRis greater than the blackhole radius of normal energy.By(3.19),the deficient energy is compensated by the dual gravitational potential,i.e.by the second term of(7.4).

Attraction and repulsion of gravity

Based on Theorem 5.1,gravity possesses additional attraction and repelling to the Newtonian gravity,as shown in the revised gravitational formula:

By using this formula we can explain the dark matter and dark energy phenomena.In particular,based on the Rubin rotational curve and astronomical data,we can determine an approximation of the parametersk0andk1in(7.6).

1)Dark matter:the additional attracting.LetMrbe the total mass in the ball with radiusrof galaxy,andVbe the constant galactic rotational velocity.By the force equilibrium,we infer from(7.6)that

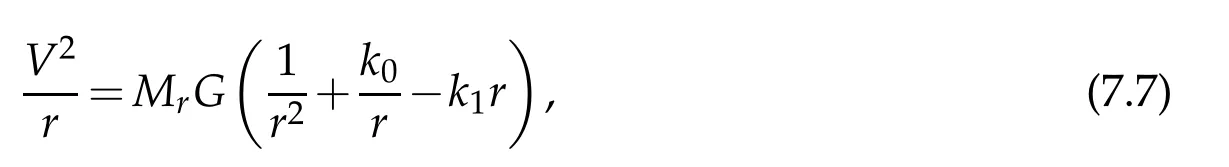
which implies that

The mass distribution(7.8)is derived based on both the Rubin rotational curve and the revised formula(7.6).In the following we show that the mass distributionMrfits the observed data.

We know that the theoretic rotational curve given by Figure 2.1(b)is derived by using the observed massMoband the Newton formula

Hence,to show thatMr=Mob,we only need to calculate the rotational curvevrby the Newton formula from the massMr,and to verify thatvris consistent with the theoretic curve.To this end,we have

which,by(7.8),leads to

Ask1≪k0≪1,vrcan be approximatively written as

It is clear that the rotational curve described by(7.9)is consistent with the theoretic rotational curve as illustrated by Figure 2.1(b).Therefore,it implies that

The facts of(7.7)and(7.10)are strong evidence to show that the revised formula(7.6)is in agreement with the astronomical observations.

We now determine the constantk0in(7.6).According to astronomical data,the average massMr1and radiusr1of galaxies are about

The observations show that the constant velocityVin the Rubin rotational curve is aboutV=300km/s.Then we have

Based on physical considerations,

Then,we deduce from(7.8)that

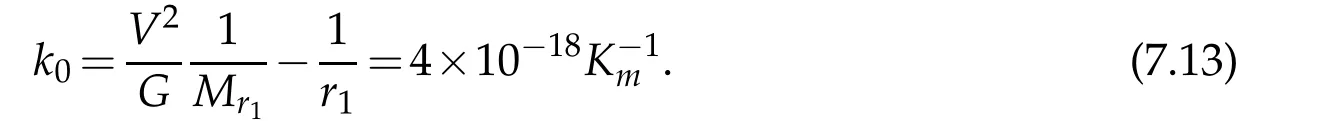
We can explain the dark matter by the revised formula(7.6).As the matter distributionMris in the form

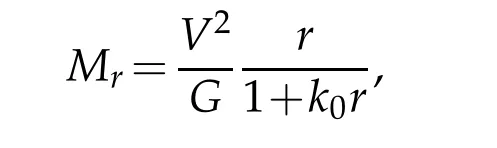
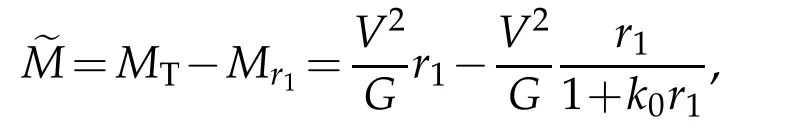
whereM1=V2r1/Gis the Newton theoretic value of the total mass.Hence we have

2)Dark energy:asymptotic repulsion of gravity.If gravity is always attracting as given by the Newton formula,then the cosmic homogeneity is unstable.In fact,It is known that the average massMand distance for the clusters of galaxies are as

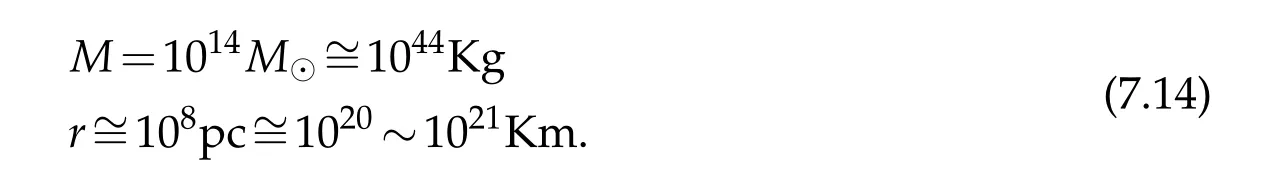
Then the Newton gravitation between two clusters of galaxies is

However,astronomical observations indicate thatno gravitational interaction between clusters of galaxies.The Universe is isotropic,therefore no rotation to balance the huge force of(7.15)in the clusters.

Thus,the new cosmology theorem,[1,Theorem 6.2],suggests that gravity should be asymptotically repulsive.Theorem 5.1 offers a solid theoretic foundation for the property,based on which we derive the simplified gravitational force formula(7.6).

Now we consider the constantk1in(7.6).Due to the astronomical fact that no gravitational force between clusters of galaxies,we have

By(7.14),we take

Then we deduce from(7.6)that

which,by(7.13)and(7.16),leads to

In summary,we conclude that the dark matter and dark energy are essentially gravitational effect generated by the gravitational potential fieldgµν,its dual field Φµand their nonlinear interactions.They can be regarded as the gravitational field energy caused bygµνand Φµ.

Acknowledgments

The authors are grateful to Micka¨el D.Chekroun for his insightful discussions.The work was supported in part by National Science Foundation(NSF)grants DMS-1049253&DMS-1515024,by Office of Naval Research(ONR)grant N00014-15-1-2662,and by a Chinese National Science Foundation grant.

[1]T.Ma and S.Wang.Astrophysical dynamics and cosmology.Journal of Mathematical Study,47(4):305–378,2014.

[2]T.Ma and S.Wang.Gravitational field equations and theory of dark matter and dark energy.Discrete and Continuous Dynamical Systems,Ser.A,34(2):335–366,2014;first appeared in arXiv:1206.5078v2.

[3]T.Ma and S.Wang.Mathematical Principles of Theoretical Physics.Science Press,Beijing,524pp.August,2015.

[4]T.Ma and S Wang.Unified field equations coupling four forces and principle of interaction dynamics.Discrete and Continuous Dynamical Systems,Ser.A,35(3):1103–1138,2015;first appeared in arXiv:1210.0448.

[5]M.Milgrom.A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis.Astrophysical Journal,270:365–370,1983.

[6]M.Milgrom.MOND laws of galactic dynamics.MNRAS,437:2531–2541,2014.

[7]S.Perlmutter G.Aldering,G.Goldhaber and et al.Measurements ofωandλfrom 42 highredshift supernovae.Astrophys.J.,517:565–586,1999.

[8]A.G.Riess,A.V.Filippenko,P.Challis and et al.Observational evidence from supernovae for an accelerating universe and a cosmological constant.Astron.J.,116:1009–1038,1989.

[9]V.Rubin and J.W.K.Ford.Rotation of the andromeda nebula from a spectroscopic survey of emission regions.Astrophysical Journal,159:379–404,1970.

[10]F.Zwicky.On the masses of nebulae and of clusters of nebulae.Astrophysical Journal,86:217–246,1937.

26 May,2015;Accepted 7 August,2015

∗Corresponding author.Email addresses:hernmarc@indiana.edu(Hernandez),matian56@sina.com(Ma),showang@indiana.edu(Wang)