Weak Convergence Theorems for Mixed Type Asymptotically Nonexpansive Mappings
Shilong Wei and Weiping Guo
College of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,Jiangsu Province,P.R.China.
Weak Convergence Theorems for Mixed Type Asymptotically Nonexpansive Mappings
Shilong Wei and Weiping Guo∗
College of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,Jiangsu Province,P.R.China.
.The purpose of this paper is to prove some weak convergence theorems for mixed type asymptotically nonexpansive mappings with mean errors in uniformly convex Banach spaces.The results presented in this paper extend the corresponding results in the references.
AMS subject classifications:47H09,47H10
Mixed type asymptotically nonexpansive mappings,uniformly convex Banach space,common fixed point,weak convergence.
1 Introduction and preliminaries
Throughout this work,we assume thatEis a real Banach space,E∗is the dual space ofEandJ:E→2E∗is the normalized duality mapping defined by

where 〈.,.〉denotes duality pairing betweenEandE∗.A single-valued normalized duality mapping is denoted byj.

A Banach spaceEis said to have theKadec−Klee property[2]if for every sequence{xn}inE,xn→xweakly and ‖xn‖→‖x‖,it follows thatxn→xstrongly.
A Banach spaceEis said to satisfyOpial′s condition[3]if for any sequence{xn}ofE,xn→xweakly asn→∞implies that

LetKbe a nonempty subset of a real normed linear spaceE.A mappingT:K→Kis said to be asymptotically nonexpansive[4]if there exists a sequence{kn}⊂[1,∞)with limn→∞kn=1 such that

for allx,y∈Kandn≥1.
A subsetKof a real Banach spaceEis called a retract ofE[5]if there exists a continuous mappingP:E→Ksuch thatPx=xfor allx∈K.Every closed convex subset of a uniformly convex Banach space is a retract.A mappingP:E→Eis called a retraction ifp2=p.It follows that if a mappingPis a retraction,thePy=yfor allyin the range ofP.
Definition 1.1.[5]LetKbe a nonempty subset of a real normed linear spaceE.LetP:E→Kbe a nonexpansive retraction ofEontoK.A nonself-mappingT:K→Eis said to beasymptotically nonexpasiveif there exists a sequence{kn}⊂[1,∞)with limn→∞kn=1 such that

for allx,y∈Kandn≥1.
LetKbe a nonempty closed convex subset of a real uniformly convex Banach spaceE.Chidumeet al.[5]studied the following iteration scheme:

for eachn≥1,where{an}is a sequence in(0,1)andPis a nonexpansive retraction ofEontoK,and prove some strong and weak convergence theorems for asymptotically nonexpansive mapping.
In 2006,Wang[6]generalized the iteration process(1.1)as follows:

for eachn≥1,whereT1,T2:K→Eare two asymptotically nonexpansive nonself-mappings and{an},{bn}are real sequences in[0,1),and prove some strong and weak convergence theorems for asymptotically nonexpansive mappings.

In 2012,Guoet al.[7]generalized the iteration process(1.2)as follows:for eachn≥1,whereS1,S2:K→Kare two asymptotically nonexpansive self-mappings andT1,T2:K→Eare two asymptotically nonexpansive nonself-mappings and{an}{bn}are real sequences in[0,1),and prove some strong and weak convergence theorems for mixed type asymptotically nonexpansive mappings.
LetEbe a real Banach space,Kbe a nonempty closed convex subset ofEandP:E→Kbe a nonexpansive retraction ofEontoK.LetS1,S2:K→Kare two asymptotically nonexpansive self-mappings andT1,T2:K→Eare two asymptotically nonexpansive nonselfmappings.Then we define the new iteration scheme of mixed type with mean errors as follows:


The purpose of this paper is to prove some weak convergence theorems for the new two-step iterative scheme in uniformly convex Banach spaces.The results presented in this paper extend the corresponding results in[5–7,10].
2 Some lemmas
In order to prove the main results,we need the following lemmas.




Thenlimn→∞‖xn−q‖exists for any q∈F.




If the following conditions hold:


Lemma 2.3.([9])Let X be a uniformly convex Banach space and C a convex subset of X.Then there exists a strictly increasing continuous convex function γ:[0,∞)→[0,∞)with γ(0)=0such that for each S:C→C with Lipschitz constant L,

for all x,y∈C and0<α<1.
Lemma2.4.([9])Let X beauniformly convex Banachspace that its dual X∗has the Kadec−Klee property.Suppose{xn}is a bounded sequence and f1,f2∈Ww(xn)(where Ww(xn))denotes the set of all weak subsequential limits of a bounded sequence{xn}in X such that

exists for all α∈[0,1].Then f1=f2.
Lemma 2.5.([5])Let E be a real uniformly convex Banach space,K be a nonempty closed convex subset of E and T:K→E be an asymptotically nonexpansive mapping with a sequence{kn}⊂[1,∞)and kn→1as n→∞.Then I−T isdemiclosed atzero,i.e.,if xn→x weakly and xn−Txn→0strongly,then x∈F(T),where F(T)is the set of fixed points of T.
3 Main results
In this section,we prove weak convergence theorems for the iterative scheme given in(1.4)in uniformly convex Banach spaces.

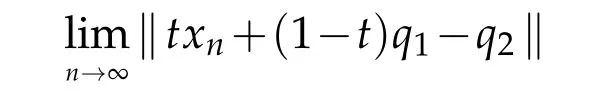
exists for all t∈[0,1],where{xn}is defined by(1.4).
Proof.Settingan(t)=‖txn+(1−t)q1−q2‖.Then limn→∞an(0)=‖q1−q2‖ and,from Lemma 2.1,limn→∞an(1)=‖xn−q2‖ exists.Thus it remains to prove Lemma 3.1 for anyt∈(0,1).
Define the mappingsHn:K→Kby

for allx∈K.It is easy to prove that



Then we have

for eachm≥1,from(3.2)and(3.3),it follows that

forallx,y∈KandSn,mxn=xn+m.Nextwe show that,forallq∈F,‖Sn,mq−q‖→0 uniformly for allm≥1 asn→∞.Indeed,for anyq∈F.we have

‖Snmq−q‖≤‖Hn+m−1···Hnq−Hn+m−1···Hn+1q‖+···+‖Hn+m−1q−q‖

It follows from

thatδn→o,asn→∞.Let

Observe that

Using(3.4)and Lemma 2.3,we have
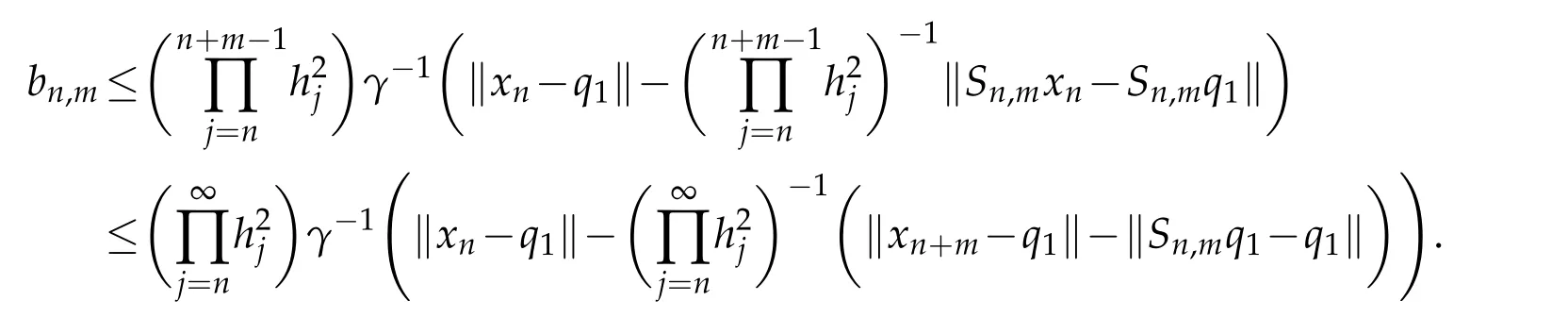

Thus,fixingnand lettingm→∞in(3.5),we have
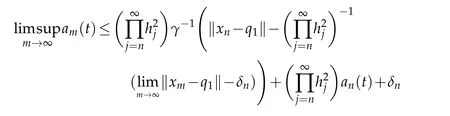
and again lettingn→∞,we obtain that

that is limn→∞‖txn+(1−t)q1−q2‖ exists for allt∈[0,1].This completes the proof.


exists,where{xn}is the sequence defined by(1.4).Furthermore,if Wω({xn})denotes the set of all weak subsequential limits of{xn},then〈x∗−y∗,j(q1−q2)〉=0for all q1,q2∈F and x∗,y∗∈Wω({xn}).
Proof.This follows basically as in the proof of Lemma 3.2 of[10]using Lemma 3.1 instead of Lemma 3.1 of[10].
Theorem 3.1.Under the assumptions of Lemma2.2,if E has a Fr´echet dif ferentiable norm,then the sequence{xn}defined by(1.4)converges weakly to a common fixed point of S1,S2,T1and T2.
Proof.SinceEis a uniformly convex Banach space and the sequence{xn}is bounded by Lemma 2.1,there exists a subsequence{xnk}of{xn}which converges weakly to someq∈K.By Lemma 2.2,we have


Now,we prove that the sequence{xn}converges weakly toq.Suppose that there exists a subsequence{xmj}of{xn}such that{xmj}converges weakly to someq1∈F.So,q,q1∈F∩Wω({xn}).It follows from Lemma 3.2 that

Therefore,q1=q,which shows that the sequence{xn}converges weakly toq.This completes the proof.
Theorem 3.2.Under the assumptions of Lemma2.2,if the dual E∗of E has the Kadec−Klee property,then the sequence{xn}defined by(1.4)converges weakly of a common fixed point of S1,S2,T1and T2.

Now,we prove that the sequence{xn}converges weakly toq.Suppose that there exists a subsequence{xmj}of{xn}such that{xmj}converges weakly to someq∗∈K.Then,as forq,we haveq∗∈F.It follows from Lemma 3.1 that the limit

exists for allt∈[0,1].Again,Sinceq,q∗∈Wω({xn}),soq=q∗By Lemma 2.4.This shows that the sequence{xn}converges weakly toq.This completes the proof.
Theorem 3.3.Under the assumptions of Lemma2.2,if E satisfies Opial′s condition,then the sequence{xn}defined by(1.4)converges weakly to a common fixed point of S1,S2,T1and T2.
Proof.SinceEis a uniformly convex Banach space and the sequence{xn}is bounded by Lemma 2.1,there exists a subsequence{xnk}of{xn}which converges weakly to someq∈K.By Lemma 2.2,we have




Thus,byOpial′s condition,we have


Remark 3.1.Theorems 3.1-3.3 extend the corresponding results in[5–7,10].
[1]M.O.Osilike and A.Udomene.Demiclosedness principle and convergence theorems for strictly pseudocontractive mappings of Bronwder-Petryshyn type.J.Math.Anal.Appl.,256:431-445,2001.
[2]K.Goebel and W.A.Kirk.Topics in Metric Fixed Point Theory,in Cambridge Studies in Advanced Mathematics.Cambridge University Press,Cambridge UK,28,1990.
[3]Z.Opial.Weak convergence of successive approximations for nonexpansive mapping.Bull.Amer.Math.Soc.,73:591-599,1967.
[4]K.Goebel and W.A.Kirk.A fixed point theorem for asymptotically nonexpansive mapping.Proc.Amer.Math.Soc.,35:171-174,1972.
[5]C.E.Chidune,E.U.Ofoedu and H.Zegeye.Strong and weak convergence theorems for asymptotically nonexpansive mapping.J.Math.Anal.Appl.,280:364-374,2003.
[6]L.Wang.Strong and weak convergence theorems for common fixed point nonself asymptotically nonexpansive mapping.J.Math.Anal.Appl.,323:550-557,2006.
[7]W.P.Guo,Y.J.Cho and W.Guo.Convergence theorems for mixed type asymptotically nonexpansive mappings.Fixed Point Theory and Applications,224,2012.
[8]S.L.Wei and W.P.Guo.Strong convergence theorems for mixed type asymptotically nonexpansive mappings,Comm.Math.Res.,31:149-160,2015.
[9]J.Schu.Weak and strong convergence of fixed point of asymptotically nonexpansive mapping.Bull.Aust.Math.Soc.,43:153-159,1991.
[10]W.P.Guo and W.Guo.Weak convergence theorems for asymptotically nonexpansive nonself-mapping.Appl.Math.Lett.,24:2181-2185,2011.
30 October,2014;Accepted 4 May,2015
∗Corresponding author.Email addresses:wslong0315@126.com(S.Wei),guoweiping18@aliyun.com(W.Guo)
 Journal of Mathematical Study2015年3期
Journal of Mathematical Study2015年3期
- Journal of Mathematical Study的其它文章
- Growth of Solutions of Higher Order Complex Linear DifferentialEquations in an Angular Domain of Unit Disc
- Elliptic Systems with a Partially Sublinear LocalTerm
- Second Order Estimates for Non-concave Hessian Type Elliptic Equations on Riemannian Manifolds
- The Distortion Theorems for Harmonic Mappings with Negative Coefficient Analytic Parts
- Global Strong Solution to the 3D Incompressible Navierv-Stokes Equations with General Initial Data
- Non-Isotropic Jacobi Spectral and Pseudospectral Methods in Three Dimensions
