数学模型对水冷型PVT围护结构热性能的影响研究

吴婷 马良栋* 张吉礼 赵天怡

大连理工大学建设工程学部

数学模型对水冷型PVT围护结构热性能的影响研究

吴婷 马良栋* 张吉礼 赵天怡

大连理工大学建设工程学部

本文针对PVT围护结构分别建立了一维传热模型和二维传热模型，分析了数学模型对水冷型PVT围护结构热性能的影响，结果表明：一维传热模型增大了冷却水得热量、墙体得热量和电池片发电量，减小了热损失，与一维传热模型的结果相比，二维传热模型由于考虑了吸热板和电池片在流体流动方向的导热，可以获得吸热板和电池片的温度分布，其计算结果具有较高的精度，对PVT围护结构的设计具有重要指导作用。

数学模型 PVT 围护结构 热性能

0 引言

太阳能光伏光热建筑一体化具有同时为建筑供电、供热（甚至供冷）、提高太阳能综合利用效率和系统经济性等优点而成为国内外学者研究的热点[1～4]，并提出了典型的空冷型[5]和水冷型[6]两种BIPVT系统形式。现有研究表明：水冷型BIPVT系统的综合热效率可达到70%以上，因此从热能利用角度看，水冷型BIPVT系统较风冷型在性能上更具有优势和应用前景[7]。水冷型PVT围护结构横截面示意图如图1所示，在电池组件的背面采用管板式水冷却系统对电池组件进行冷却，以提高电池组件的效率。在对平板式太阳能集热器吸热板进行传热分析时，一维的H-W理论分析模型得到了大量应用[8]，在此基础上，D.W.de Vries[9]对该模型进行了修正，使其适用于太阳能光伏光热组件传热分析。D.W.de Vries理论模型的建立对太阳能光伏光热组件的结构设计及其热效率分析具有重要作用，但该模型也存在一定的缺陷，如：假设各吸热管内的流体流量是均匀的；忽略吸热板沿流体流动方向的传热；尽管考虑了电池与吸热板之间的热阻对效率因子进行了修正，但仍假设电池与吸热板的温度是一致的。但对于实际的光伏光热组件，首先，通过联箱向各换热管内分配流体，其流量是不均匀的，流量分配不均将导致组件热效率的变化。Chiou[10]通过人为假定每根换热管内流量分布研究流量分布不均匀性对集热器热效率的影响，其结果表明由于流量的不均性导致集热器热效率减少2%～20%；Wang和Wu[11]研究顺流和逆流两种模式下集热器的热效率。与逆流相比，顺流情况下换热管内的流量分布比较均匀，因此，与逆流模式相比，顺流模式下热效率提高了14%，达到58.5%。其次，通常情况下吸热板的导热系数较高，换热管沿流动方向温度升高，导致吸热板的温度沿流动方向温度也相应升高，因此，沿流动方向吸热板的导热是需要考虑的；第三，对于PVT围护结构，由吸热板经建筑墙体向室内的导热量是很重要的一个参数，吸热板温度对其计算结果的精度具有决定性的影响，因此，假设电池与吸热板的温度一致是不合理的。本文针对PVT围护结构建立了准三维传热数学模型，研究该模型对PVT围护结构光热效率、热损失及围护结构传热量的影响，对太阳能光伏光热建筑一体化的系统设计及围护结构负荷计算具有重要意义。

图1 PVT围护结构横截面示意图

1 PVT围护结构物理及数学模型

1.1 物理模型

水冷型PVT围护结构由玻璃盖板、PV集成组件、吸热板及建筑围护结构构成。换热管管内流体通过联箱管分配，且换热管之间为同程连接，相邻两根换热管间距为W，换热管外径为Do，内径为Di，PV集成组件由单晶硅电池（125mm×125mm）通过串联和并联组成，其电池参数如表1所示。上层玻璃盖板贴附在光伏电池上，光伏组件与吸热板之间用导热性能良好的胶粘贴。水冷型PVT围护结构宽为1.25m，长为1.8m，其结构示意图见图2所示，结构及物性参数见表2。

表1 单晶硅电池参数

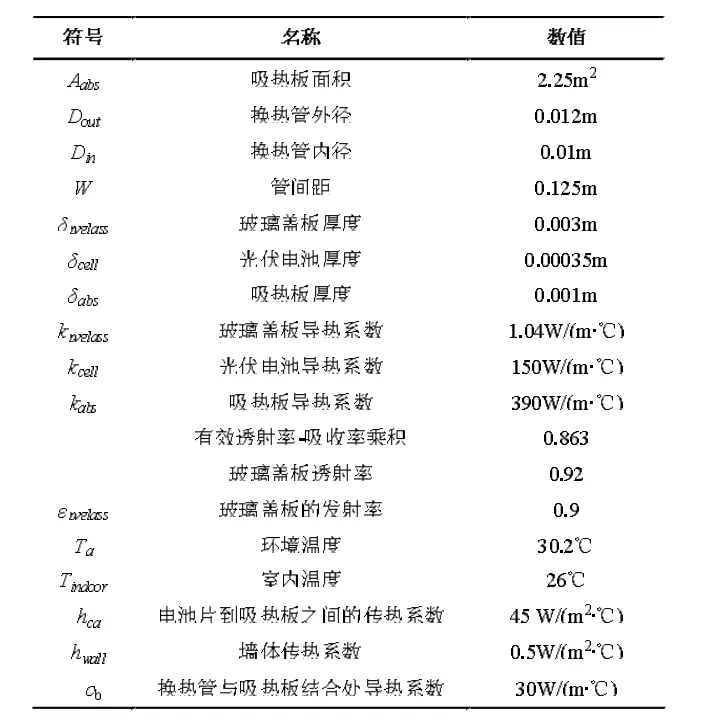
表2 水冷型PVT围护结构结构及物性参数

1.2 二维稳态传热数学模型

针对PV集成组件和吸热板建立二维传热数学模型。为简化模型，作如下假设：

1）传热为稳定状态；

2）联箱管的传热忽略不计；

3）忽略自然对流对换热管管内流体流动的影响，且管内流体质量流量已知；

4）忽略玻璃盖板和建筑围护结构沿流体流动方向（y方向）及横向（x方向）的传热。

PV组件二维传热方程

吸热板二维传热方程

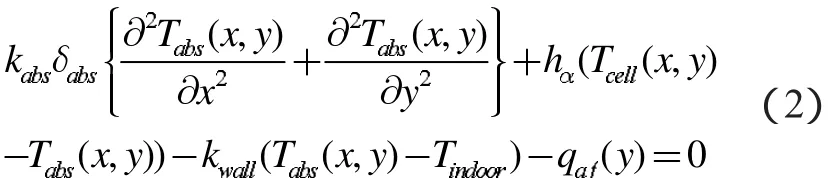
ηel为电池效率，可以表示为

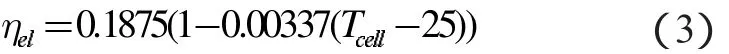
qaf为单位面积吸热板传给换热流体的热量

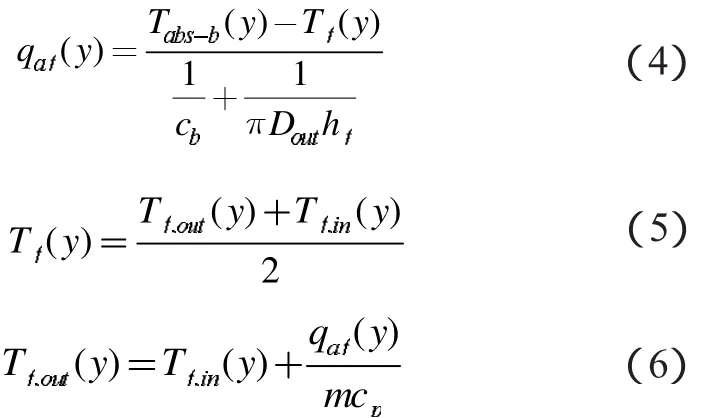
当管内为层流时，管内换热系数为hf=700W/ (m2·℃)[12]；若为湍流，则管内换热系数通过式（7）确定。

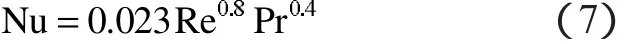
热损失系数Uloss能被表示为

式（1）和式（2）的边界条件分别如下

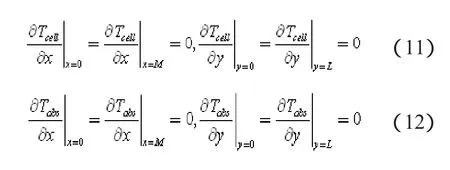
1.3 一维稳态传热数学模型

基于图2（b）所示的能量平衡[9]，吸热板和玻璃盖板的平均温度能被分别表示为

热损失

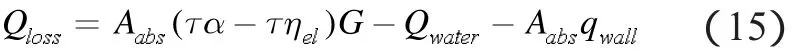
围护结构传热量

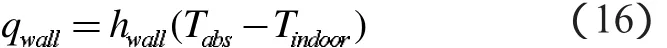
换热流体得到的热量

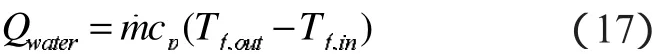
流体出口温度

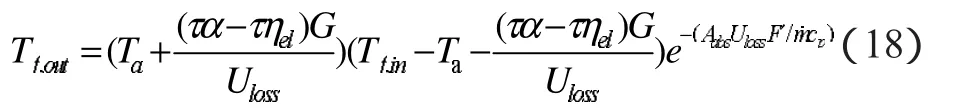
其中

2 模型验证

针对二维传热模型，采用控制容积对其进行离散，方程离散后的代数方程采用三对角阵算法（TDMA）进行求解。PVT电池组件和吸热板采用非均匀网格进行网格划分，在换热管处，网格较密，见图3所示。为了确认二维传热模型及开发程序的正确性，将开发程序应用于文献[11]中的顺流问题。其计算参数为：换热流体进口温度Tin=16℃，太阳辐照度G=700W/m2，空气温度Ta=21.5℃，热损失系数Uloss=9W/(m·℃)，换热管直径为0.014m，换热管间距为0.1875m，吸热板面积为3m2，换热管根数为16根，换热管内的流体质量流量按文献[11]的计算值给出。图4给出了每根换热管热效率，从图中可以看出，通过二维传热模型计算的换热管热效率略高于参考计算值，其最大绝对误差为3%；二维传热模型平均热效率比参考计算平均热效率大1.5%，这主要是由于在二维传热模型中忽略了联箱管的传热，因此热效率略有偏大。图4的结果表明，本文开发的PVT围护结构二维传热计算模型及程序是正确的，可以用于吸热板及电池组件温度分布的求解。

图3 网格划分示意图

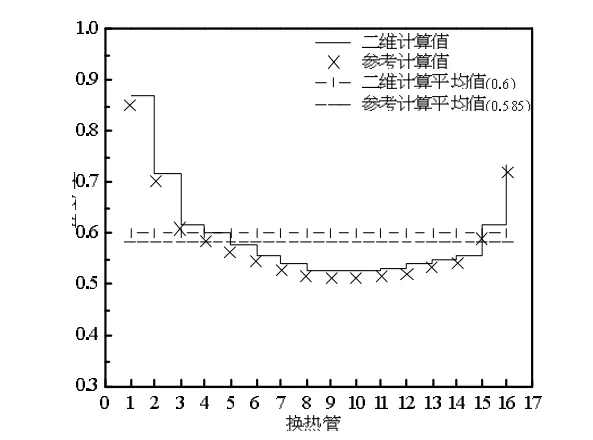
图4 换热管热效率比较

3 计算结果分析

本文研究对象的吸热体面积为2.25m2，换热管根数为10根，且均匀布置，冷却水质量流量为0.015kg/ (s·m2)，换热流体分配到各根换热管质量流量通过Fluent模拟计算获得，见图5。从图6可以看出，水冷型PVT围护结构的热损失qloss、墙体得热量qwall、冷却水得热量qwater和电池片发电量qe皆随着太阳辐射照度的增大而增加；一维传热模型的冷却水得热量、墙体得热量和电池片发电量皆大于二维传热模型，冷却水得热量相对偏差最大值为2.8%，电池片发电量相对偏差最大值为10.4%，墙体得热量相偏差随太阳辐照度的增大而增大，偏差最大值为56.6%；一维传热模型的热损失小于二维传热模型的结果，热损失相对偏差最大值为28%。其主要原因是随着太阳辐照度的增大，一维模型吸热板的平均温度大于二维模型吸热板的温度且小于二维模型电池片的平均温度，见图7所示，且随太阳辐射照度的增大，吸热板温度之间的相对偏差增大，因此，采用一维传热模型时，墙体的得热量计算结果偏大，这与实际情况是不相符的，结果表明，采用简化的一维传热模型分析PVT围护结构传热特性将产生较大的误差。

图5 每根换热管的质量流率

从图8可以看出，水冷型PVT围护结构的冷却水得热量qwater和电池片发电量qe皆随着流体进口温度的升高而减小，热损失qloss和墙体得热量qwall皆随着流体进口温度的升高而增大；一维传热模型的冷却水得热量、墙体得热量和电池片发电量皆大于二维传热模型的计算结果。冷却水得热量相对偏差随换热流体入口温度升高而增大，其最大值达到10.8%；墙体得热量相对偏差随换热流体入口温度的升高而减少，其最大值为146%，最小值为3.5%；电池片发电量相对偏差最大值为12.5%。同太阳辐照度增大一样，一维传热模型的热损失小于二维传热模型的结果，但热损失相对偏差最大值为25%。其主要原因是随着换热管流体进口温度的增加，一维模型吸热板的平均温度皆大于二维模型吸热板平均温度，其差值逐渐减小；一维模型吸热板的平均温度皆小于二维模型电池片的平均温度，其差值逐渐增大，如图9所示。

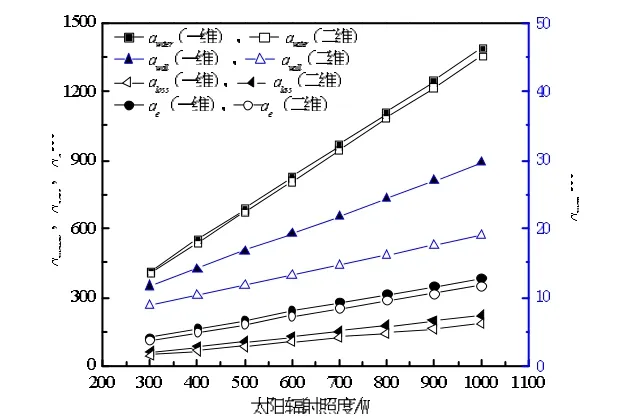
图6 PVT围护结构各物理量随太阳辐射照度的变化曲线

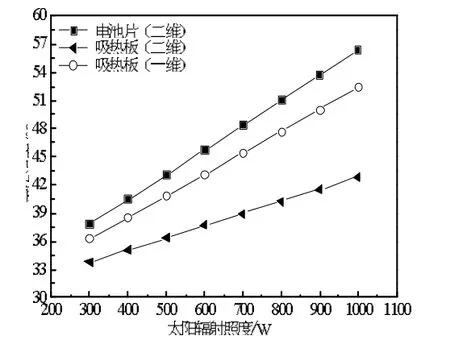
图7 吸热板平均温度随太阳辐照度的变化

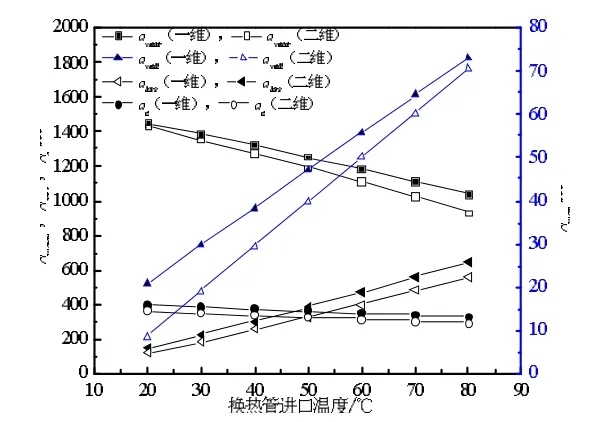
图8 PVT围护结构各物理量随流体进口温度的变化

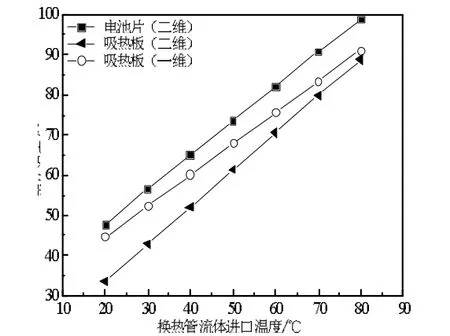
图9 吸热板平均温度随流体进口温度的变化

4 结论

本文针对PVT围护结构分别建立了一维传热模型和二维传热模型，分析了数学模型对水冷型PVT围护结构热性能的影响，与一维传热模型计算结果相比，二维传热模型具有较高的计算精度。尽管一维传热模型将电池与吸热板之间的热阻对效率因子进行了修正，但仍假设电池与吸热板的温度是一致的，同时忽略了换热流体流动方向的导热，导致一维传热模型吸热板温度偏高，但对于电池组件温度来讲，温度偏低，因此其对墙体传热量及热损失影响较大，其结果表明，对于PVT围护结构，需针对PVT组件各层，如吸热板、电池片等分别建立二维传热模型，获得吸热板和电池片的温度分布，对提高PVT围护结构的墙体传热量、热损失、冷却水得热量等物理量的计算精度具有重要作用。

[1]胡晨明,怀特RM著,李采华译.太阳能电池[M].北京:北京大学出版社,1990

[2]van Helden W G J,van Zolingen R J C,Zondag H A.PV thermal systems:PV panels supplying renewable electricity and heat[J]. Progress in Photovoltaics:Research and Applications,2004,12 (6):415-426

[3]Zondag H A,De Vries D W D,Van Helden W G J,et al.The thermal and electrical yield of a PV-thermal collector[J].Solar energy,2002,72(2):113-128

[4]Erdil E,Ilkan M,Egelioglu F.An experimental study on energy generation with a photovoltaic(PV)solar thermal hybrid system [J].Energy,2008,33(8):1241-1245

[5]Gan G.Numerical determination of adequate air gaps for building -integrated photovoltaics[J].Solar Energy,2009,83(8):253-1273

[6]Dubey S,Tiwari G N.Thermal modeling of a combined system of photovoltaic thermal(PV/T)solar water heater[J].Solar Energy,2008,82(7):602-612

[7]安文韬,刘彦丰.太阳能光伏光热建筑一体化系统的研究[J].应用能源技术,2007,11:33-36.

[8]Duffie J A,Beckman W A.Solar engineering of thermal processes[M].New York:John Wiley&Sons,2013

[9]Zondag H A,De Vries D W D,Van Helden W G J,et al.The ther -mal and electrical yield of a PV-thermal collector[J].Solar energy,2002,72(2):113-128

[10]Chiou J P.The effect of nonuniform fluid flow distribution on the thermal performance of solar collector[J].Solar Energy,1982,29 (6):487-502

[11]S A Wang,L G Wu.Analysis and performance of flat-plate solar collector arrays[J].Solar Energy,1990,45(2):71-78

[12]赵丹,马良栋,赵天怡,等.U型圆管内混合对流换热特性数值研究[J].建筑热能通风空调,2013,32(5):5-9

Effe c tof Ma the m a tic a l Mode l onThe rm a l Pe rform a nc eof aBuilding Enve lope Inte gra te d Wa te r-c oole d Sola r PVT Sys te m

WU Ting,MA Liang-dong*,ZHANG Ji-li,ZHAO Tian-yi
Faculty of Infrastructure Engineering,Dalian University of Technology

The one-dimensional and two-dimensional heat transfer models of a building envelope integrated solar PVT system were established.The effects of mathematical models on thermal performance of the PVT envelope were analyzed.The results show that the heat gain of cooling water,heat transfer rate by conduction through the wall,and the photovoltaic yield increase,while heat loss through the top glass decrease using the one-dimensional heat transfer model. The results of two-dimensional heat transfer model have a higher accuracy compared with those of one-dimensional heat transfer model,because the heat transfer by conduction along direction of fluid flow is considered for the absorber plate and the cells in two-dimensional heat transfer model,the temperature distribution of the absorber plate and the cells can be attained.The results have an important guiding function for the design of the PVT envelope.

mathematical model,PVT envelope,thermal performance

1003-0344（2015）05-001-5

2014-5-10

马良栋（1976～），男，博士，副教授；辽宁省大连市大连理工大学建设工程学部（116024）；E-mail:liangdma@dlut.edu.cn

“十二五”国家科技支撑计划（2013BAJ10B02）