基于定标器相位梯度提取的圆迹SAR轨迹重建方法
郭振宇 林 赟 洪 文 谭维贤 王彦平
基于定标器相位梯度提取的圆迹SAR轨迹重建方法
郭振宇*①②③林 赟①②洪 文①②谭维贤①②王彦平①②
①(中国科学院电子学研究所 北京 100190)②(微波成像技术国家重点实验室 北京 100190)③(中国科学院大学 北京 100049)
圆迹合成孔径雷达(CSAR)高分辨率成像,对惯导系统的精度和稳定性提出了更高的要求,运动补偿技术是关键技术之一。该文首先分析了轨迹测量误差引起的相位误差,然后针对相位误差的空变性给出一种基于定标器相位梯度提取的圆迹SAR轨迹重建方法。该方法从SAR回波数据中提取定标器沿方位向的相位梯度,结合多个定标器的相位梯度,利用三边测量法重建高精度圆迹SAR轨迹,用于获取高质量的CSAR图像。该方法解决了轨迹测量误差引起的图像散焦问题,可实现整个场景的有效聚焦。仿真结果验证了该方法的正确性和有效性。
合成孔径雷达;圆迹合成孔径雷达;运动补偿;轨迹重建;相位梯度
1 引言
圆迹SAR(CSAR)作为20世纪90年代提出的一种SAR工作模式[1],不同于传统条带SAR斜平面成像几何,具有对场景区进行3维重建[2,3]的能力。此外,圆迹SAR的全方位观测能够有效减小常规SAR固有的阴影现象,并且对于获取目标随方位角变化的后向散射信息具有重要意义。基于这些独特优势,圆迹SAR一经提出便受到广泛的关注。
2004年开始,法国航空航天研究院(ONERA)、瑞典国防研究院(FOI)、德国宇航中心(DLR)以及中国科学院电子学研究所等研究机构相继利用机载试验平台开展了圆迹SAR飞行试验[4,5]。2011年7月,德国宇航中心首次展示了利用E-SAR机载系统获取的L波段全极化全方位高分辨圆迹SAR图像[6]。2011年8月,中国科学院电子学研究所开展了国内首次圆迹SAR飞行试验,成功获取了P波段全极化全方位高分辨圆迹SAR图像。文献[10~12]利用全极化多基线圆迹SAR(MultiCircular SAR)数据对森林地区进行了3维重建。与常规条带SAR图像相比,圆迹SAR图像展现了更为丰富和精细的地物信息,初步展示了圆迹SAR在高精度测绘、灾害评估和目标检测[13]等领域的应用潜力。
与常规条带SAR相比,圆迹SAR对导航测量系统有着更高的要求。为了实现高质量聚焦,成像的相位误差需要控制在,即轨迹测量误差需要控制在波长的1/16。常规条带SAR合成孔径小,合成孔径时间短,惯导系统在短时间内能保证较高的相对测量精度,然而圆迹SAR的合成孔径时间长达数分钟[12],一方面惯导系统难以在如此长的时间内保持较好的稳定性,另一方面累计误差将降低整个轨迹的相对测量精度,此外,惯导系统对于曲线运动平台的测量有更大的误差。在运动补偿方面,机载条带SAR即使波段较高,一般只需基于定位定向系统(Position and Orientation System, POS)数据进行运动补偿即可满足聚焦成像要求,或者在此基础上再使用自聚焦技术就可获得较高的聚焦质量,而当圆迹SAR的波段较高时(C波段及以上),由于现有的轨迹测量精度有限,基于POS数据的运动补偿已无法满足其聚焦成像的要求[14],需要寻求基于回波数据的补偿方法[15]。目前成功获得全方位高分辨机载圆迹SAR图像的试验所采用的波段都较低(P和L),还未见能解决高波段圆迹SAR对高精度导航测量系统依赖性问题的方法。
本文提出了一种基于定标器回波相位梯度提取的圆迹SAR高精度轨迹重建方法,利用场景中放置的定标器,从SAR回波中提取定标器的相位梯度,借助定标器的几何坐标重建整个圆迹SAR轨迹,该方法不依赖于高精度惯导系统,并能有效控制相位误差,提高成像质量。
2 测量误差引起的相位误差
测量误差是指SAR平台做圆周飞行时其轨迹的测量值和真实值之间的差,测量值通过导航系统获得,系统精度越高,该误差越小,这种空间坐标的测量误差在进行SAR成像时将转变成方位向的相位误差。而SAR成像的基本原理是相干积累,因此相位误差将影响积累时的相干性,最终影响成像质量。
图1是圆迹SAR成像几何示意图,假设平台的真实坐标为,测量坐标为,场景中有一目标,平台围绕场景中心做圆周运动并发射信号,雷达波束始终指向场景中心。

图1 圆迹SAR成像几何
则目标的回波信号经过距离向脉冲压缩后为(不考虑天线方向性影响)
3 基于定标器相位梯度提取的圆迹SAR轨迹重建方法
由于轨迹本身存在测量误差,因此基于POS数据的运动补偿方法并不适用,需要寻求基于回波数据的运动补偿方法。德国宇航中心通过在空旷场景中放置单个龙伯球[6],在回波数据频域估计龙伯球的相位误差,利用时频关系反推相位误差的方位时域形式,然后将补偿到回波数据,获取了Kaufbeuren机场的L波段全孔径图像。从试验结果分析龙伯球得到了精确聚焦,然而这种方法没有考虑相位误差的空变性,在成像场景较小、波段较低时可以适用,波段较高时无法对大场景进行补偿。
对于单个定标器,可以直接提取相位误差并补偿,而当场景中有多个定标器时,各定标器的相位误差不一致,无法用统一的误差形式进行补偿,然而利用真实轨迹进行成像能够使所有目标的相位误差为零,因此对SAR轨迹进行重建并成像的方法能够有效缓解误差的空变性问题。基于这种思想,本文提出了一种从回波数据中提取定标器的相位梯度,利用该相位梯度信息和定标器的测量坐标,通过三角测量法重建SAR轨迹的方法,使得重建轨迹成像时目标的相位梯度和其真实相位梯度接近,从而控制相位误差,同时相比直接补偿相位误差的方法,其能有效控制误差的空变性,扩大成像区域。
图2为该算法的总体流程图,首先回波数据经过1维距离向脉冲压缩,利用轨迹和定标器坐标的粗测量值,从脉冲压缩数据中提取3个定标器的相位梯度信息,将梯度信息转化为各定标器的距离徙动,最后通过三角测量法结合定标器坐标重建SAR轨迹。其主要步骤分为定标器的相位梯度提取以及轨迹重建两个部分,下面将分别对这两部分加以阐述。

图2 圆迹SAR轨迹重建算法流程图
3.1定标器相位梯度提取
由式(1)可得,1维脉冲压缩后的信号中包含目标的真实距离徙动,本节将通过相位梯度提取的方法来估计各个定标器的距离徙动。直接对式(1)求相位得到的是定标器相位历程在的折叠值,不能反映目标的真实距离徙动,然而SAR在方位向是离散采样的,一般情况下定标器的相位梯度不会超过,因此可先沿方位向提取相位梯度,然后累积求和计算定标器的相位历程。图3为相位梯度提取的算法流程图。首先借助粗精度的轨迹和定标器坐标,可从脉冲压缩信号中提取定标器的距离徙动线,完成对定标器数据的定位。其次在徙动线上沿方位向提取定标器的相位梯度,最后通过累计的方法估计其真实距离徙动。
选择定标器而非场景中的目标有以下几个优势:(1)定标器RCS较大,具有较高的回波信噪比,有利于提高相位提取的精度。(2)由式(1)可知,脉冲压缩信号中还包含有目标自身的后向散射相位,选择合适的定标器如龙伯球或全向三面角反射器,可使不随观测角变化而变化,减小对相位梯度的影响,而目标的散射相位是未知的。(3)定标器的相位中心在几何上是已知的,可直接测量其相位中心坐标,提高轨迹重建的精度。
如图3所示,通过场景中放置定标器并测量其相位中心的坐标,计算定标器到测量轨迹距离,即距离徙动的测量值。

图3 相位梯度提取流程图
方位滤波后的信号为
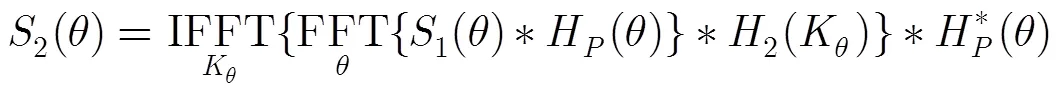
由式(1)可知,该常数项引起的相位误差也为常数,在成像时不影响成像结果。
3.2轨迹重建
上一节讨论了从回波数据中提取定标器的相位梯度并估计其距离徙动,本节将利用多个定标器的距离徙动重建高精度圆迹SAR轨迹。
如图1,假设场景中有3个定标器,,,其均为各向同性,通过测量其坐标为,,。通过上一节得到它们的估计距离徙动为,,。根据三边测量法,已知3点坐标及空间中一点到它们的距离,可以重建出该点的3维坐标。根据该原理,通过式(9)对轨迹坐标进行重建。
4 仿真实验
为验证本文算法的有效性,按表1所示的参数进行点目标仿真实验。

表1仿真参数
如图4所示,在场景中同时放置定标器和9个点目标阵,验证其成像效果。其中三角形实心点为3个定标器,,,坐标为(0,500), (-500,-500), (500,-500),图4(b)为9个点目标阵的放大图,点目标阵以目标5(1000,0)为中心,相邻间隔为0.5 m。
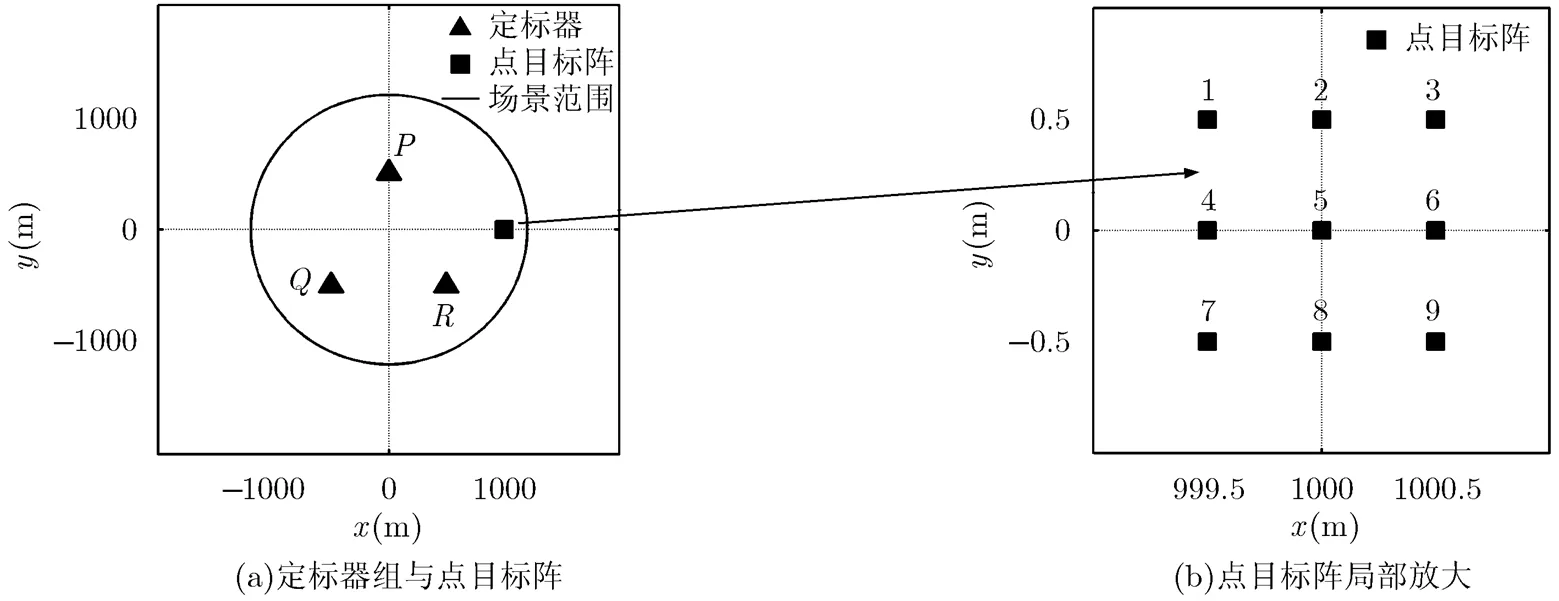
图4 仿真场景
为了说明轨迹精度对成像的影响,图5分别示出了在轨迹精度为5 cm, 1 cm, 3 mm情况下,使用测量轨迹成像时定标器的成像结果,从图中可知,对各向同性目标,圆迹SAR的轨迹精度要达到才能获得良好聚焦的图像。

图5 轨迹定位误差对成像的影响
为了说明相位误差的空变性影响,图6展示了将定标器的相位误差补偿于场景边缘区域的结果,其中,图6(a)为定标器未进行相位补偿的结果,图6(b)为对定标器进行相位误差估计并补偿的结果,图6(c)为将估计的定标器的相位误差补偿至点目标阵的成像结果,可见定标器在补偿后得到了精确聚焦,而由于相位误差空变性的存在,场景边缘区域补偿结果并不理想。

图6 相位误差的空变性影响

图7 圆迹SAR重建轨迹、测量轨迹与真实轨迹
图8(a)从左至右分别为使用测量轨迹、真实轨迹、重建轨迹的点目标阵成像结果,经过比较,使用重建轨迹进行成像其聚焦性能良好,图8(b), 8(c)为定标器和点目标5在重建轨迹下的局部放大图,两个目标均得到良好的聚焦,由表2可知,定标器和目标的成像结果参数与理论值接近,因此重建轨迹不仅适用于定标器的聚焦,对定标器以外的目标其空变的相位误差也得到了控制,体现了该方法对圆迹SAR空变性相位误差的适应性。

表2重建轨迹下成像结果参数

图8 成像结果比较
图9从相位误差的角度分析了重建轨迹对相位误差的控制,图9中实线为重建轨迹相对真实轨迹引起的相位误差,虚线为测量轨迹引起的相位误差,横坐标代表方位向,图9(a)为定标器的相位误差,图9(b)为点目标5的相位误差。在惯导系统精度受限影响下,测量轨迹引起的相位误差幅度均超过,沿方位向是随机变化的,因此在该误差存在下目标无法聚焦。在重建轨迹下,定标器的相位误差为常数,该常数相位由重建轨迹的初始值决定,虽然其幅度超过,但其相位梯度误差为零,不影响成像质量,与前面所述一致,图9(b)中重建轨迹的相位误差为缓变正弦形式,其相位误差梯度也被控制在较小的范围内。
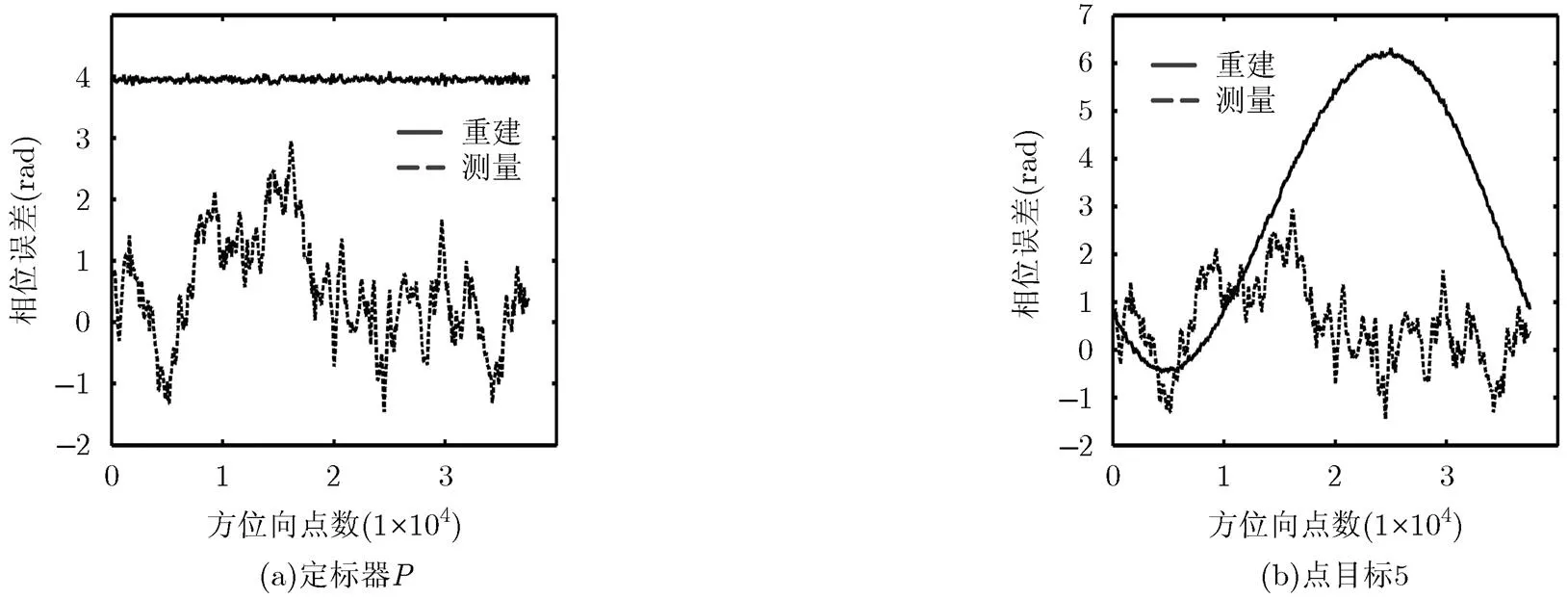
图9 重建轨迹与测量轨迹的相位误差
5 结束语
圆迹SAR具备的高分辨率成像和全方位观测能力可获取更丰富的目标信息,然而现阶段圆迹SAR的高质量成像依赖高于精度惯导系统,针对上述问题,本文给出了一种不依赖于高精度惯导系统的圆迹SAR运动补偿方法,通过提取已知定标器的相位梯度获取其高精度距离徙动变化量,利用三边测量法对轨迹进行重建,以补偿轨迹定位误差引起的空变性相位误差。仿真结果中目标的分辨率、峰值旁瓣比等成像指标验证了算法的有效性。在实际的机载圆迹SAR数据处理时,此方法对定标器回波数据的信杂比要求需要进一步的研究。
参考文献
[1] Soumekh M. Synthetic Aperture Radar Signal Processing[M]. New York, John Wiley & Sons, 1999: 486-539.
[2] Pinheiro M, Prats P, Scheiber R,.. Tomographic 3D reconstruction from airborne circular SAR[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2009), Cape Town, 2009, 3: III-21-III-24.
[3] Demirci S, Yigit E, and Ozdemir C. Wide-field circular SAR imaging: 2D imaging results for simulation data[C]. 2013 6th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, 2013: 421-424.
[4] Frolind P, Gustavsson A, Lundberg M,.. Circular- aperture VHF-band synthetic aperture radar for detection of vehicles in forest concealment[J]., 2012, 50(4): 1329-1339.
[5] Frolind P, Ulander L M H, Gustavsson A,.. VHF/ UHF-band SAR imaging using circular tracks[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2012),Munich, 2012: 7409-7411.
[6] Ponce O, Prats-Iraola P, Pinheiro M,.. Fully polarimetric high-resolution 3-D imaging with circular SAR at L-band[J]., 2013, 52(6): 3074-3090.
[7] 洪文. 圆迹 SAR 成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135.
Hong Wen. Progress in circular SAR imaging technique[J]., 2012, 1(2): 124-135.
[8] 林赟, 谭维贤, 洪文, 等. 圆迹 SAR 极坐标格式算法研究[J]. 电子与信息学报, 2010, 32(12): 2802-2807.
Lin Yun, Tan Wei-xian, Hong Wen,.. Polar format algorithm for circular synthetic aperture radar[J].&, 2010, 32(12): 2802-2807.
[9] Lin Y, Hong W, Tan W,.. Airborne circular SAR imaging: Results at P-band[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS),Munich, 2012: 5594-5597.
[10] Ponce O, Prats-Iraola P, Scheiber R,.. Analysis and optimization of multi-circular SAR for fully polarimetric holographic tomography over forested areas[C]. 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, 2013: 2365-2368.
[11] Ponce O, Prats-Iraola P, Scheiber R,.. Polarimetric 3-D reconstruction from multicircular SAR at P-band[J]., 2014, 11(4): 803-807.
[12] Ponce O, Prats P, Rodriguez-Cassola M,.. Processing of circular SAR trajectories with fast factorized back- projection[C]. 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2011), Vancouver, 2011: 3692-3695.
[13] Poisson J B, Oriot H, and Tupin F. Performances analysis of moving target tracking in circular SAR[C]. 2013 14th International IEEE Radar Symposium(IRS), Dresden, Germany, 2013, 1: 531-536.
[14] Cantalloube H and Koeniguer E C. Assessment of physical limitations of high resolution on targets at X-band from circular SAR experiments[C]. 7th European Conference on Synthetic Aperture Radar (EUSAR 2008), Friedrichshafen, 2008: 1-4.
[15] Dungan K E and Nehrbass J W. Wide-area wide-angle SAR focusing[J]., 2014, 29(1): 21-28.
Circular SAR Trajectory Reconstruction Based on Phase Gradient of Calibrators
Guo Zhen-yu①②③Lin Yun①②Hong Wen①②Tan Wei-xian①②Wang Yan-ping①②
①(,,100190,)②(,100190,)③(,100049,)
Circular SAR (CSAR) high resolution imaging requires a more accurate and stable Inertial Navigation System (INS), therefore motion compensation is one of the key technologies. In this paper, the phase error caused by trajectory measurement error is firstly analyzed. Then, the CSAR trajectory reconstruction algorithm based on the extraction of calibrators’ phase gradient is proposed. This algorithm is aiming at the spatial variant property of phase errors. The azimuth differential phase of each calibrator is extracted from SAR echo data. The high precision CSAR trajectory is reconstructed via trilateration in combination with multiple calibrators’ phase gradient. The high quality CSAR image is formed with this trajectory. The proposed algorithm solves the problem of image defocusing by trajectory measurement error, meanwhile the entire scene gets focused efficiently. The simulation results verify the correctness and effectiveness of the proposed algorithm.
SAR; Circular SAR (CSAR); Motion compensation; Trajectory reconstruction; Phase gradient
TN958
A
1009-5896(2015)08-1836-07
10.11999/JEIT140950
郭振宇 ggfuji@gmail.com
2014-07-17收到,2015-05-07改回,2015-06-09网络优先出版
郭振宇: 男,1988年生,博士生,研究方向为圆迹SAR成像算法.
林 赟: 女,1983年生,助理研究员,研究方向为合成孔径雷达3 维成像技术.
洪 文: 女,1968年生,研究员,研究领域为雷达信号处理理论、合成孔径雷达成像算法、微波遥感图像理解及其应用等.

