基于复数信息传递的结构稀疏宽角合成孔径雷达成像算法

蒋成龙 张冰尘 王正道 洪 文



基于复数信息传递的结构稀疏宽角合成孔径雷达成像算法

蒋成龙*①②③张冰尘①②王正道④洪 文①②

①(微波成像技术国家重点实验室 北京 100190)②(中国科学院电子学研究所 北京 100190)③(中国科学院大学 北京 100049)④(爱荷华州立大学 美国)

传统相关处理算法不能完全解决宽角合成孔径雷达(WASAR)成像中目标的散射特性随观测角度变化的问题。稀疏信号处理为该问题提供一种新思路，各向异性问题可以建模成欠定方程组。随角度增大，未知量的规模以观测孔径数目的线性规模增长，导致成功重建难度增大，甚至是重建失败。该文提出一种基于信息传递原理的宽角合成孔径雷达成像方法。根据宽角合成孔径雷达的观测几何及目标散射特性在不同角度之间存在的相关性，建立基于结构稀疏的成像模型；然后利用信息传递原理，提出基于结构稀疏复数信息传递(GCAMP)的成像算法求解该成像模型。仿真结果验证了该方法的有效性。

合成孔径雷达；宽角合成孔径雷达成像；各向异性散射特性；结构稀疏；信息传递

1 引言

宽角合成孔径雷达(Wide Angle SAR, WASAR)[1]指的是合成孔径角度满足使方位向分辨率大于距离向分辨率要求的一类合成孔径雷达观测模式。为实现这类大角度观测，除了需要所观测的回波数据在较长持续时间内保持相干特性之外，同时还要求获得这段时间内雷达平台的精确位置信息，这得益于现代高精度实时的全球定位系统、惯性导航系统。目前主流的WASAR成像算法包括后向投影算法、极坐标格式算法等。由于收集了很大角度范围内观测目标的雷达后向散射信息，所以WASAR可以得到高分辨率的雷达图像，从而提供了常规SAR所不具备的目标识别与可视化的潜力。

WASAR成像需要考虑目标随观测角度变化的散射特性。由于叠掩、闪烁现象以及目标非理想几何特性等因素，目标的散射信息在WASAR观测角度范围内存在较大变化，使用常规成像算法难以发挥WASAR的潜在优点。目前有一系列方法被提出以解决该问题。文献[2]提出基于滤波器的方法，将目标散射特性函数作为卷积核对方位向回波信号进行滤波，从而得到目标散射系数的峰值，但是由于目标的散射类型并非精确已知，非理想滤波造成信噪比损失以及分辨率降低；另外相干累积时间减少，各向同性目标的信噪比也会下降，图像的动态范围减小。文献[3]提出改进的滤波器方法，采用矩形窗函数作为卷积核，并设定门限对各向异性目标采用自适应方法成像、对其他目标采用全孔径方法成像。这种方法提高了各向同性目标的成像信噪比，保持了图像的动态范围，同时计算复杂度从降为，但是依然面临分辨率降低的问题。上述这些方法都是通过相关处理完成成像过程，并不能充分实现WASAR模式的优点。

稀疏微波成像[4]为解决WASAR成像的各向异性问题提供另一种思路。文献[5]在子孔径成像中利用稀疏正则化方法增强目标分辨能力的思路，在一定程度上解决了子孔径成像导致分辨率降低的问题，但该方法未充分利用整个观测孔径内目标的散射信息。文献[6]通过建立过完备字典的方式结合稀疏信号处理方法进行成像。过完备字典中包含了目标散射特性的所有组合。由于实际目标散射特性只是字典中子集，所以问题的解是稀疏的，能够利用稀疏方法求解，但该方法所求问题存在较严重的欠定性，且未知量是方位向观测数的平方量级，只适合处理非常稀疏的场景。文献[7,8]假定目标散射特性在局部观测角度内的具有一定相关性且变化较小，提出了一种联合稀疏恢复的方法。该方法针对子孔径方法和过完备字典方法都有所改进，但是其所构建模型存在一定的矛盾性，且所求解问题仍具有病态性，没有较高效的求解算法。文献[9]将WASAR成像的各向异性问题等效成SAR视频成像问题，利用隐性马尔科夫过程对各向异性目标的散射特性建模，并提出利用动态压缩感知的方法进行成像。该方法可在一定程度上降低问题的病态性，但是其散射模型在限制了对整个观测孔径内目标的散射信息的利用。WASAR的理想平台轨迹可以是直线或者圆弧。圆迹合成孔径雷达(Circular SAR, CSAR)[10,11]是一种典型的WASAR观测模式，雷达平台相对观测目标作近似圆周运动，雷达波束始终照射目标场景区域，形成目标2维孔径，可实现对目标的3维观测。文献[12]提出了利用稀疏信号处理方法进行CSAR成像。考虑目标各向异性时，利用稀疏方法求解CSAR成像问题的难度更大。

由上可知，现有基于稀疏信号处理的WASAR成像中各向异性问题的未知量数目以观测孔径的线性规模增长，随着WASAR合成孔径角度增大，问题出现严重的欠定性，难以使用常规稀疏微波成像算法处理该类问题。为了解决上述问题，本文提出一种基于信息传递原理的WASAR成像方法。首先根据WASAR观测模型及目标散射特性随角度变化的特点，建立基于结构稀疏的WASAR成像模型；利用信息传递原理，提出基于结构稀疏复数信息传递(Group-sparse Complex Approximately Message Passing, GCAMP)的WASAR成像算法；再对GCAMP算法的具体实施提出了一种基于逆成像算子的有效实现方法。本文安排如下：第2节介绍基于结构稀疏的WASAR成像模型；第3节根据成像模型提出基于GCAMP的WASAR成像算法；第4节利用实验结果说明所提算法的有效性；最后给出总结。

2 基于结构稀疏的宽角SAR成像模型

假定目标的散射特性随角度变化，则WASAR的回波可以表示为

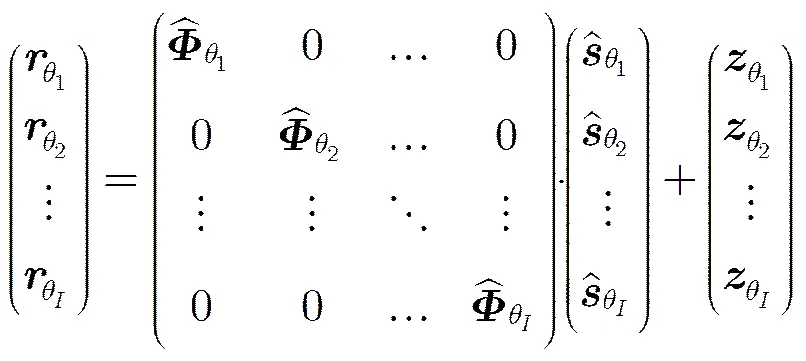
简写为

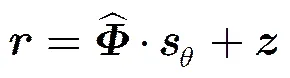
考虑到实际场景中，并非所有目标的反射系数都随观测角度变化而改变，均匀球体、某些自然地物以及背景杂波等目标的散射特性可以视为各向同性的；而大多数人造目标的散射特性则可合理地视为各向异性。所以，观测模型中可以包含此类信息。WASAR的观测模型最终可表示为

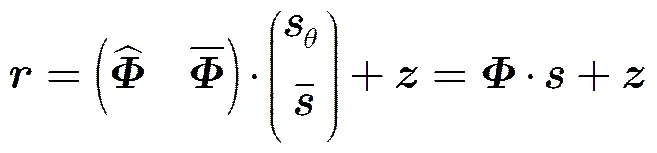
文献[7,8]指出目标散射特性在小范围观测角度内的变化较小，在相邻观测角度内存在一定相关性，成像时可利用这种信息降低稀疏重建难度。事实上，对的这种信息可以利用结构稀疏性来描述。结构稀疏性是传统信号稀疏性的扩展，其针对对象是组并且允许组内元素存在广泛的结构性特征。WASAR成像中的未知量相比于传统SAR成像的未知量多了观测角度这一维度。对按照不同目标分组，记为同一目标在不同观测角度下的反射系数，则基于结构稀疏的WASAR成像模型表示为

3 基于GCAMP的WASAR成像算法

稀疏信号处理中的信息传递(Approximate Message Passing, AMP)算法的技术细节可以参考文献[13, 14]。其中文献[13]较早提出AMP算法，文献[14]提出复数的AMP算法并进行相应的性能分析。本节根据基于结构稀疏的WASAR模型，利用信息传递原理给出GCAMP算法。

3.1算法推导

其中

3.2参数设置

3.3快速计算

在3.1节算法实现时，可利用逆成像算子替代矩阵构建，实现有效计算，其主要原理是利用逆成像算子代替矩阵与向量的乘法运算[15,16]，WASAR成像中主要以逆后向投影(Back Projection, BP)算子构建。由于GCAMP算法的主要计算量来自于矩阵与向量相乘运算，其计算复杂度约为。利用逆成像算子进行快速计算后，可以利用离散傅里变换以及1维处理替代矩阵向量运算，虽然计算量接近于，但是由于不需要构建观测矩阵，可减少对存储空间的需求。

本节主要利用了AMP算法原理解决实际WASAR的成像问题，所提算法与目前已发表的关于AMP算法的文献相比，存在如下两处主要的技术创新点：首先，所提算法需要求解如第1节所述的问题模型，该模型具有与已有文献的问题模型不同；其次，所提算法针对是复数未知量且实部与虚部是条件独立的随机变量，未知量之间采用结构稀疏性约束。

4 实验

实验主要目的是验证本文提出的GCAMP算法能够有效重建WASAR各向异性目标的雷达后向散射系数。主要参数为：发射信号载频5.3 GHz，带宽100 MHz，采样率150 MHz，脉宽，天线长度0.9 m，脉冲重复频率91 Hz，平台飞行半径1000 m，高度3000 m，平台速度200 m/s，实验观测角度，重建时假定目标反射系数在范围内不变。

实验场景分简单场景和复杂场景两组，如图1所示。简单场景仅包含点目标：4个各向异性目标和1个各向同性目标。各向异性目标的雷达后向散射系数响应为sinc形式，主瓣宽度，其朝向分别与右侧水平线成,,和夹角，各向异性目标之间相互间距8 m，构成正方形，中心是各向同性目标，所有目标的最大雷达后向散射系数均设置为1。复杂场景包含了点目标和分布目标：方形围框状物体，其厚度为0.4 m，向外呈现出二面角的特点，认为是各向异性目标，其幅度为10，相位满足0到间的随机分布；其中包围着的均匀的理想分布目标，幅度为1，相位同样为0到间随机分布。各向异性目标的雷达后向散射系数响应为sinc形式。各向异性目标的朝向分别为和。

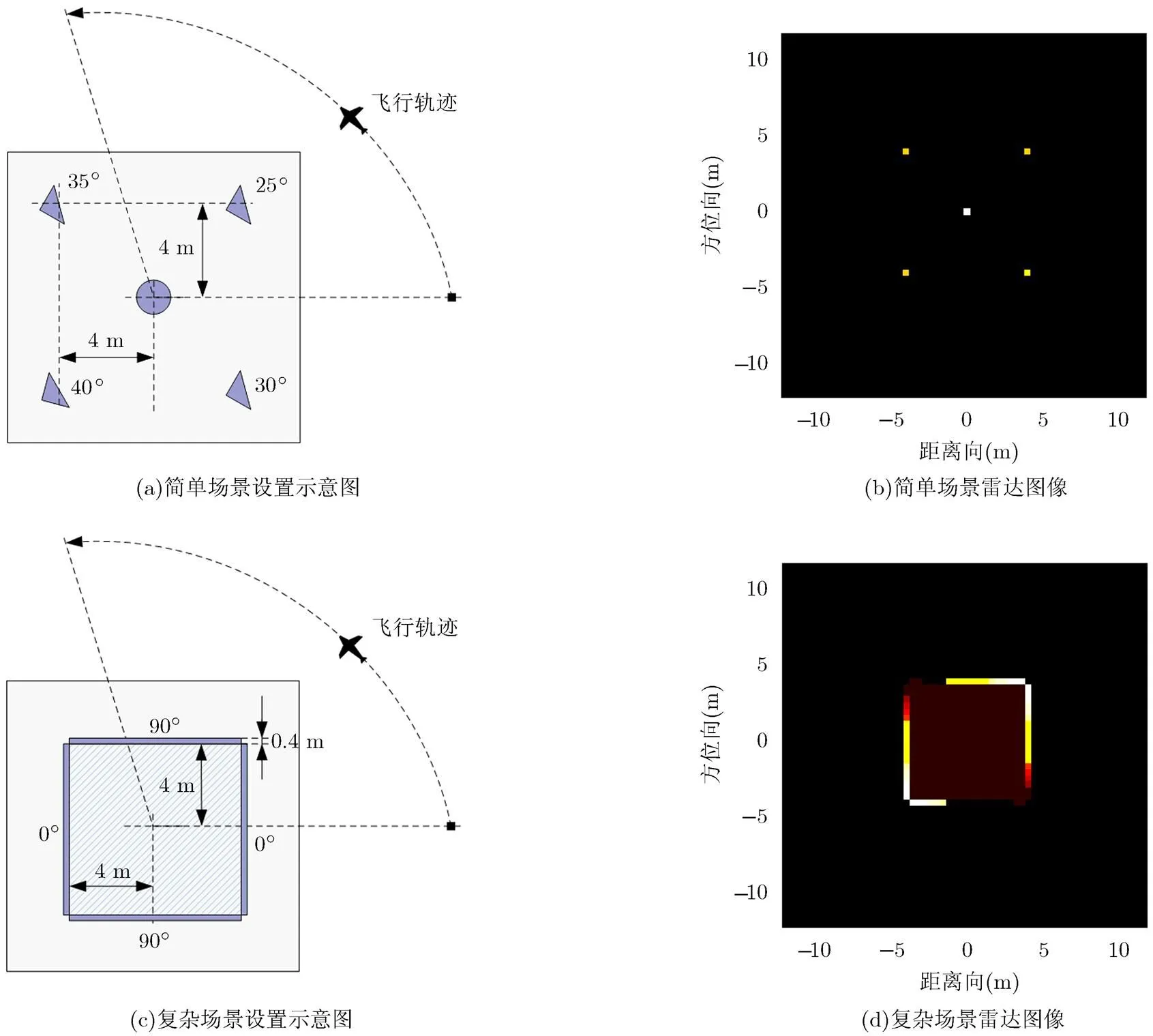
图1 实验场景及目标真实值

图2是简单场景下，传统BP算法对全孔径数据成像的结果，利用常规稀疏成像IST算法对子孔径数据成像后利用信噪比最大原则得到的综合图像结果(迭代100次)，利用常规结构稀疏成像算法得到的综合图像结果(迭代100次)以及利用本文算法得到的综合图像结果(迭代30次)。由图可知利用本文算法可以提高重建质量，缩短重建时间。

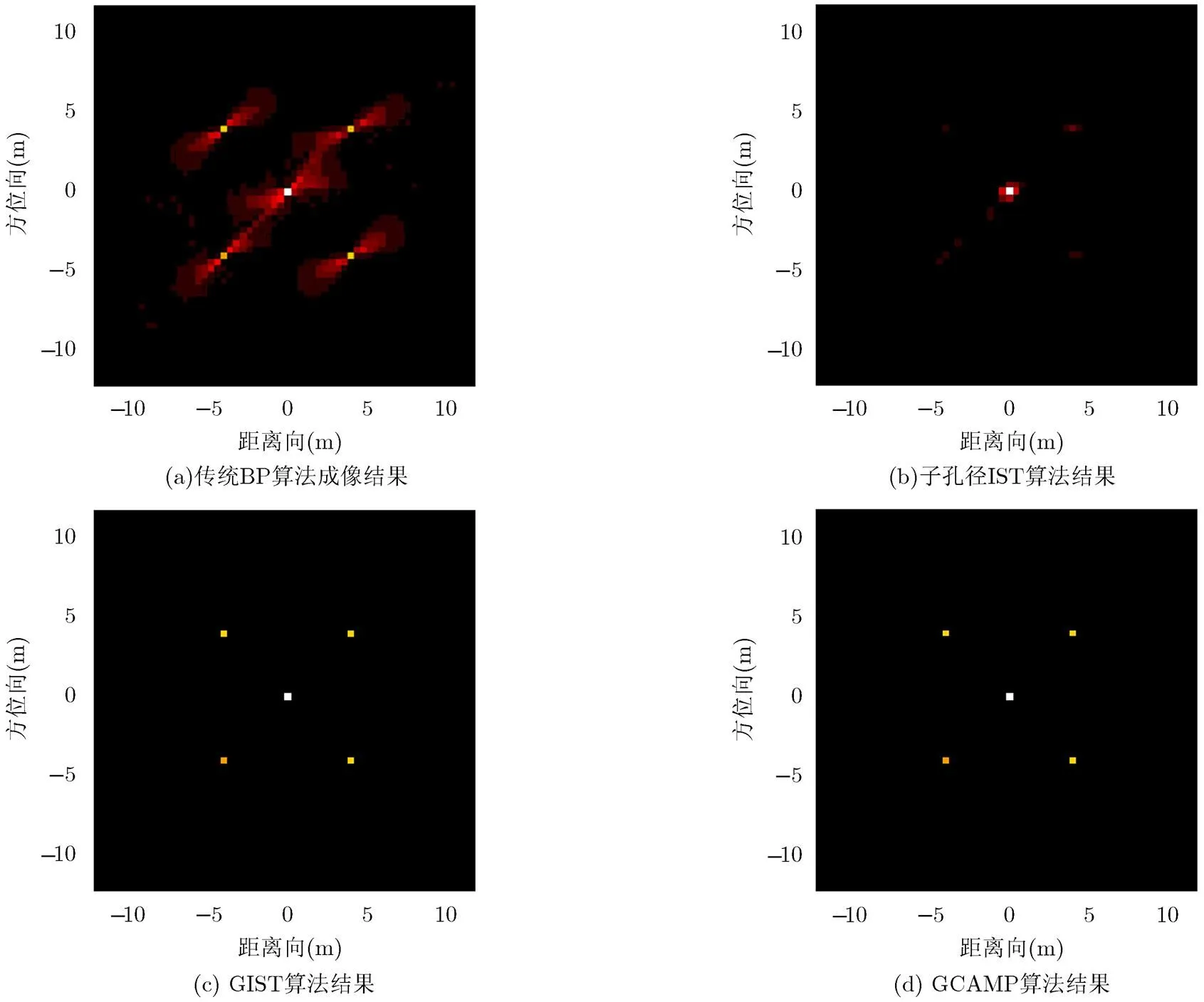
图2 场景的重建结果(全部观测角度内的综合图像)

图3是图2中的5个目标在不同观测角的反射系数曲线。其中，图3(a)是各向同性目标的反射系数曲线；图3(b), 3(d)分别是中心与右水平线呈,,夹角的各向异性目标的反射系数曲线。粗实线代表真实值，右三角点线代表利用IST算法对子孔径数据成像结果，圆框线代表利用GIST算法得到的结果，星形点虚线代表利用GCAMP算法得到的结果。从图上可以看出，GCAMP算法可以同时重建各向同性和各向异性目标的反射系数，与真实值相当吻合。

图3 重构算法得到的目标反射系数随角度变化曲线

图4是复杂场景目标的重建结果。在分布式目标与各向异性目标都存在的情况下，采用结构稀疏建模和算法能构获得更好的成像效果。具体表现在：在GIST算法和GCAMP算法的结果中，方形框状物体基本得到重建，而且目标的形状轮廓得到保持，在BP算法中存在的强旁瓣在GIST和GCAMP中基本被去除，取而代之的是类似随机噪声一般的点状干扰。在IST算法中，则基本不能重建出目标。

图4 复杂场景的重建结果(全部观测角度内的综合图像)

5 结束语

本文提出了基于结构稀疏的WASAR成像方法，可以针对性地解决WASAR中目标散射的各向异性问题，相比于常规方法，具有收敛速度快、重建误差小等优点。实验验证了所提方法的有效性。

参考文献

[1] Jakowatz C V, Wahl D E, Eichel P H,. Spotlight-mode Synthetic Aperture Radar: A Signal Processing Approach[M]. Norwell, MA, US, Kluwer Academic Publishers, 1996: 62-94.

[2] Allen M R, Phillips S A, and Sofianos D J. Wide-angle SAR-matched filter image formation for enhanced detection performance[C]. Proceedings of the International Society for Optics and Photonics in Substance Identication Technologies, Innsbruck, Austria, 1993: 381-387.

[3] Chaney R D, Willsky A S, and Novak L M. Coherent aspect-dependent SAR image formation[C]. Proceedings of the International Society for Optics and Photonics in SPIE,s International Symposium on Optical Engineering and Photonics in Aerospace Sensing, Orlando, FL, USA, 1994, 256-274.

[4] Moses R L, Potter L C, and Cetin M. Wide-angle SAR imaging[C]. Proceedings of the International Society for Optics and Photonics in Defense and Security, Orlando, FL, USA, 2004: 164-175.

[5] Zhang B C, Hong W, and Wu Y R. Sparse microwave imaging: principles and applications[J]., 2012, 55(8): 1722-1754.

[6] Varshney K R, Cetin M, Fisher J W,. Joint image formation and anisotropy characterization in wide-angle SAR[C]. Proceedings of the International Society for Optics and Photonics in Defense and Security Symposium, Orlando, FL, USA, 2006: 62370D.

[7] Stojanovic I, Cetin M, and Karl W C. Joint space aspect reconstruction of wide-angle SAR exploiting sparsity[C]. Proceedings of the SPIE Defense and Security Symposium, Orlando, FL, USA, 2008: 697005.

[8] Cetin M, Stojanovic I, Onhon O,. Sparsity-driven synthetic aperture radar imaging: reconstruction, autofocusing, moving targets, and compressed sensing[J]., 2014, 31(4): 27-40.

[9] Ash J, Ertin E, Potter L,. Wide-angle synthetic aperture radar imaging: models and algorithms for anisotropic scattering[J]., 2014, 31(4): 16-26.

[10] 林赟, 谭维贤, 洪文, 等. 圆迹SAR极坐标格式算法研究[J]. 电子与信息学报, 2010, 32(12): 2802-2807.

Lin Yun, Tan Wei-xian, Hong Wen,. Polar format algorithm for circular synthetic aperture radar[J].&, 2010, 32(12): 2802-2807.

[11] 洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135.

Hong Wen. Progress in circular SAR imaging technique[J]., 2012, 1(2): 124-135.

[12] Austin C D, Emre E, and Moses R L. Sparse signal methods for 3-D radar imaging[J]., 2011, 5(3): 408-423.

[13] Donoho D L, Maleki A, and Andrea M. Message-passing algorithms for compressed sensing[J]., 2009, 106(45): 18914-18919.

[14] Maleki A, Laura A, Yang Z,. Asymptotic analysis of complex LASSO via complex approximate message passing[J].,2013, 59(7): 4290-4308.

[15] Fang J, Xu Z B, Zhang B C,. Fast compressed sensing SAR imaging based on approximated observation[J]., 2014, 7(1): 352-363.

[16] Jiang, C L, Zhang B C, Fang J,. Efficientlregularisation algorithm with range-azimuth decoupled for SAR imaging[J]., 2014, 50(3): 204-205.

Group-sparse Complex Approximate Message Passing Algorithm for Wide Angle Synthetic Aperture Radar Imaging

Jiang Cheng-long①②③Zhang Bing-chen①②Wang Zheng-dao④Hong Wen①②

①(,100190,)②(,,100190,)③(,100049,)④(,)

Conventional matched filtering based algorithms are not sufficiently good at dealing with the anisotropic backscattering behavior of targets in Wide Angle SAR (WASAR) imaging. Sparse signal processing provides a new idea for this problem, the anisotropic problem is modeled as a group of under-determined linear equations. However, the scale of unknowns in the under-determined equations is in linear order of the number of the observation angle. As the observation angle increases, the anisotropic problem becomes more and more difficult to be solved, even failed for conventional sparse signal processing algorithms. This paper presents a Group- sparse Complex Approximated Message Passing (GCAMP) algorithm for WASAR imaging. Firstly, a group sparse based WASAR imaging model is provided according to the structured property of backscattering coefficients across different observation angles. Secondly, the GCAMP algorithm is derived from the imaging model using message passing theory. Results of simulation demonstrate the effectiveness of the proposed algorithm.

SAR; Wide Angle SAR (WASAR) imaging; Anisotropic backscattering; Group sparse; Message passing

TN957.52

A

1009-5896(2015)08-1793-08

10.11999/JEIT141300

蒋成龙 chenglong.j@gmail.com

2014-10-11收到，2015-05-11改回，2015-06-09网络优先出版

国家973计划项目(2010CB731905)资助课题

蒋成龙： 男，1987 年生，博士生，研究方向为SAR 信号处理、稀疏微波成像系统设计与信号处理.

张冰尘： 男，1973 年生，博士，研究员，研究方向为信号与信息处理、雷达信号处理与系统设计.

王正道： 男，1974年生，博士，教授，博士生导师，研究方向为通信信号处理、信息论、数据分析等.

洪 文： 女，1968 年生，博士，研究员，博士生导师，研究方向为信号与信息处理、雷达信号处理与系统设计.