基于信息熵−模糊谱聚类的非均质碎屑岩储层孔隙结构分类

葛新民，范宜仁，唐利民，陈义国，齐林海，邢帅



基于信息熵−模糊谱聚类的非均质碎屑岩储层孔隙结构分类

葛新民1, 2，范宜仁1, 2，唐利民3，陈义国4，齐林海5，邢帅6

(1. 中国石油大学地球科学与技术学院，山东青岛，266580；2. 中国石油大学CNPC测井重点实验室，山东青岛，266580；3. 中国石油大庆油田井下作业分公司，黑龙江大庆，163000；4. 陕西延长石油(集团)有限责任公司研究院，陕西西安，710075；5. 中国石油大庆油田海拉尔石油勘探开发指挥部，黑龙江大庆，163000；6. 中国石油集团测井有限公司长庆事业部，陕西西安，710201)

提出基于信息熵−模糊谱聚类算法的孔隙结构自动分类技术，应用谱聚类算法解决凸分布聚类问题，实现全局收敛，有效避免“维数灾难”。根据信息熵理论对谱聚类算法中的尺度参数进行优化，得到孔隙结构类型。在此基础上，结合模糊数学算法得到每个样本对孔隙结构类型的隶属度，根据隶属度最优法则(样品对某一类孔隙结构的隶属度大于70%)确定不同样本所属孔隙结构类别。研究结果表明：该算法所得孔隙结构分类结果与试油、试采等生产测试结果十分吻合，工程应用效果十分明显。

非均质碎屑岩；孔隙结构分类；模糊谱聚类算法；信息熵；尺度参数优化

碎屑岩的孔隙结构特征及孔隙类型是储层评价的重要内容，不同孔隙结构储层具有不同的物性、含油性、测井响应等特征，进而影响储层的产能。通过诸如铸体薄片、扫描电镜、核磁共振、毛管压力及常规物性分析等岩石物理实验进行储层孔隙结构定性描述、定量分析，进而提取相关孔隙结构表征参数进行孔隙结构划分是通过实验分析储层类型的重要思路。应用特征参数进行储层和孔隙结构类型的划分，除了交会图外，聚类分析、灰色关联等算法的应用也十分广泛。Dyman等[1]应用因子分析和聚类分析定量研究了蒙大拿州西南地区中白垩纪砂岩的岩石物理和孔隙结构相的特征。王本鉴等[2]根据模式识别和专家系统建立了不同类别储层的判定模型。刘顺生等[3]应用对应分析和聚类分析选取了储层分类参数，并结合专家分类意见确定了最佳储层分类系统。姚萌等[4]应用多元逐步回归分析和Q型聚类分析对枣南油田孔一段储层进行了综合分类。蔡忠等[5]探讨了灰色聚类分析在储集层分类评价中的应用。吴东胜等[6]应用模糊聚类分析法进行了储层类别划分并建立了评价标准。张顶学等[7]提出了基于模糊物元欧氏贴近度分析的储层分类方法。Dubois等[8]对比了贝叶斯判别、模糊逻辑分类器和人工神经网络分类器在岩相及孔隙结构分类中的应用效果。焦创赟等[9]对压汞分析数据进行聚类分析，研究了鄂尔多斯白豹油田长4+5的储层类型。张晓东等[10]结合层次分析法和模糊数学评判法建立了蜀南气田嘉二段储层的分类标准。Genty等[11]对核磁共振横向弛豫时间谱进行高斯函数拟合并得到特征参数，结合Bayes判别研究了孔隙结构识别方法。杨波等[12]应用Q型分层聚类算法进行了储层分类研究。Rodolfo等[13]应用改进的流动单元指数实现了孔隙类型的划分。Emad等[14]应用极限学习和支持向量机方法进行了碳酸盐岩储层的岩相识别。何琰[15]建立了基于模糊综合评判与层次分析的储层定量评价模型。王礼常等[16]对比了判别分析和决策树在致密砂岩气藏储层分类的准确率。谭锋奇等[17]对比了基于划分、基于层次、基于模型和基于密度的4种聚类算法在储层分类中的效果，优选基于划分的K-means算法作为砾岩油藏储层分类方法。非均质碎屑岩储层孔隙结构复杂、各向异性严重等特征往往使得常规聚类和识别算法在孔隙结构分类中难以取得理想效果。本文作者引入谱聚类方法进行孔隙结构分类，应用信息熵理论和模糊算法优化聚类结果，得到最佳孔隙结构类型及样本。

1 谱聚类算法基本原理

谱聚类算法是建立在谱图理论的基础之上，将数据的划分转化为对图的分割问题，与样本数据的维数无关。与传统聚类算法相比，具有能在任意形状的样本空间上聚类和全局收敛的优点，在处理高维数据方面具有明显的优势。设={1，2，…，g}(其中，g(1≤≤)为第个孔隙结构特征参数，为特征参数个数)，={1，2，…，s}表示实验样品构成的集合(其中s(1≤≤)为同一样品的所有孔隙结构特征参数，为样品个数)，由所有样品构成的孔隙结构特征参数矩阵为[18−20]

式中：p, j为第个样品的第种孔隙结构特征参数。

根据图的相关理论将孔隙结构分析数据映射为高维空间中的点，并以样本为节点构造图=(，)(其中，为待聚类的样本集，=×表示节点间的边界)。2个节点和之间的边权值的元素可写为

式中：(s，s)为两节点的欧氏距离，一般为||s−s||2；为尺度参数。对任意，和，均有0≤W≤1。

边权值反映2节点间的相似程度，W越大，表明2节点属于同一类的可能性也越大。由边权值组成的矩阵称为边权矩阵。与节点连接的所有节点的边权和称为度d：

由度d构成的对角阵称为度矩阵，可写为

因此，Laplacian矩阵可定义为

对进行特征值分解得到特征值(=1，2，…，)，设1≥2≥…≥λ。相邻特征值的差值(称为谱隙)为

取前个特征值(=1，2，…，，＜)及对应的特征向量(=1，2，…，，＜)组成新的×矩阵，每1行可看成是维空间的1个向量，然后用K-means聚类算法对个向量进行聚类分析。样品的类别数与具有紧密的联系，当孔隙结构类内分布越紧密，类间分布越分离时相应的δ也越大，孔隙结构类别数可用下式确定：

确定孔隙结构类别数后，选择Laplacian矩阵的前个特征向量构造新的矩阵，并对行向量进行归一化得到矩阵，即

对矩阵进行K-means聚类，则得到每个孔隙结构样本所属的孔隙结构类别。谱聚类算法的基本流程如图1所示[21]。表征孔隙结构的微观参数有很多，针对所取岩心开展常规孔渗、铸体薄片、核磁共振和核磁共振成像等实验，得到孔隙度、渗透率、圆度、形状因子、比表面、纵横比、非均质性系数、迂曲度、2几何平均值、2算术平均值、孔隙半径、分维数(分别表示为，，D，F，/，R，，，2L，2M，和NMR)共12种特征参数。

图1 谱聚类算法的基本流程

Fig. 1 Basic flow of spectrum clustering algorithms

相关系数是反映变量间密切程度的重要指标。对于2个变量和，若它们的样本值分别为x和y(=1，2，3，…，；为样本个数)，两者的相关系数为

式中：为数学期望；cov表示协方差。

当＞0时为正相关，当＜0时为负相关。对取绝对值，越大说明相关程度高。相关系数矩阵是由多个相关系数组成的矩阵，对12个孔隙结构参数进行相关分析可得相关矩阵，矩阵中。经分析得相关矩阵为

从式(11)得到关联程度后，选择相关系数小、正交性强的6个参数作为表征孔隙结构的特征向量。计算每个参数与其他参数的相关系数之和可得

式中：为变量的总相关系数。

通过相关系数的排序确定孔隙结构特征参数为F，R，，，和NMR。

2 信息熵法优化尺度参数

算法中尺度参数需人工输入，给分类结果带来一定误差。图2和图3所示分别为不同的特征值与谱隙分布。从图2和图3可见：随着尺度参数的增大，特征向量的差异逐渐减小，越大(当为0.2时，=5；当为0.5时，=9)。尺度参数对聚类结果影响非常大，如何优化选取尺度参数是谱聚类方法亟待解决的关键问题。引入信息熵理论进行尺度参数优化，其本质是对信息熵求极小。信息熵描述离散随机变量不确定性程度。若变量是所有信息的集合，()是属于的概率，则变量的信息熵为[22]

(a) 特征向量分布；(b) 谱隙分布

(a) 特征向量分布；(b) 谱隙分布

当对所有信息的概率均相等时熵最大，即当()=1/时()=log。信息熵越小，则不确定性越小，信息量也越小。数据集信息熵越小，则说明数据分布越散；数据集信息熵越大，则说明数据分布越集中。

对边权矩阵，定义概率函数

边权矩阵信息熵为[23]

边权矩阵与尺度参数有关，信息熵是尺度参数的函数。当→0时，(x)→1/，此时()最大，即()=log。当由0逐渐增至时，()开始逐渐减小并在某个时达最小，然后逐渐增大，当→∞时再达到最大[23]。样本的()与关系如图4所示。从图4可知：当为0.122时，()达极小(2.656)，因此，选择0.122为最优尺度参数。最优尺度参数下的谱隙分布如图5所示。谱隙最大时为5，因此，将孔隙结构分为5类。

图4 信息熵与尺度参数的关系

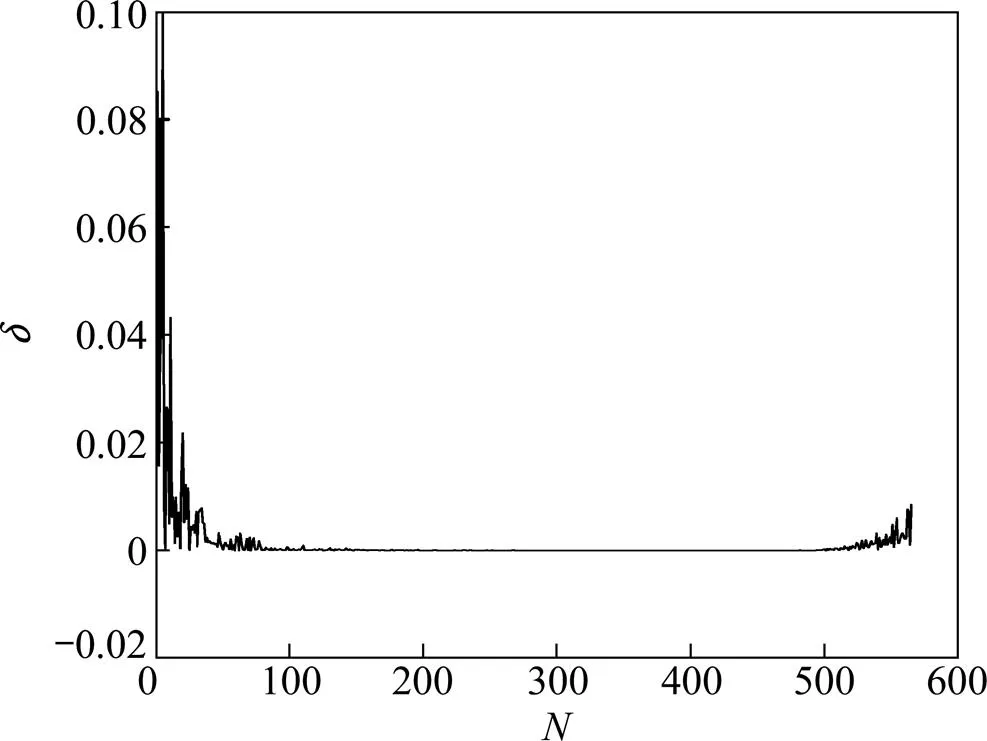
图5 最优尺度参数下的谱隙分布

3 模糊算法确定孔隙结构类别和最优样本

谱聚类算法中通过对新矩阵进行K-means聚类分析确定每个样本所属类型。K-means算法是一种硬聚类方法，输出的隶属度只有0和1，而实际样本往往存在一些模糊信息，譬如某样本兼有A和B两类的性质，但隶属于A类的可能性较大，因此，需通过隶属度来进行判断类的属性，这种算法称为模糊聚类法。应用模糊聚类法得到每个样本的隶属函数后通过最大隶属函数准则实现样品的聚类。

对于给定样本集={1，2，…，s}，每个样本中的特征参数有个，其模糊聚类划分空间中的个模糊子集满足：

式中：u为第个样本在第类的隶属度。

类内加权误差平方和目标函数为

式中：为×阶正定矩阵。当为单位阵时，d为欧氏距离。

2次计算u距离满足收敛条件时得到。模糊聚类算法的步骤[25]如下。

1) 给定初始化参数和并计算初始；2) 根据式(19)和式(20)更新和；3) 给定，若找到1个合适的范数矩阵使则停止迭代，否则转步骤2)。

得到距离最小时各样品在不同类中的隶属度u并根据最大隶属度原则即可确定所有样本的类别。本文中的最优样本是指对某类隶属度大于0.75的样本，隶属度越大，表明样本所属类别的确定性强。通过基于信息熵的模糊谱聚类算法对样本分析得到488个最优样本，其中：第I类86个，第II类122个，第III类96个，第IV类78个，第V类106个。

4 不同孔隙结构类型的微观特征 分析

应用信息熵−模糊谱聚类算法将储层孔隙结构分为5类后可得每类孔隙结构的微观结构特征，应用“岩心刻度测井”可得每类孔隙结构储层的产液性质。I类孔隙结构的铸体薄片、核磁共振横向弛豫时间谱等实验结果如图6所示(由于核磁共振信号与孔隙度有关,根据核磁共振谱幅度的累加可刻度成孔隙度，因此，不同横向弛豫时间所对应的信号幅度可转换成孔隙度分量)。从图6可见：孔隙度分布在18.4%~25.7%之间，平均为20.88%；渗透率(气测法)分布在54.71×10−3~ 688.45×10−3μm2之间，平均为236.2×10−3μm2；岩石以中粒为主，分选较好，磨圆以次棱为主，泥质含量较小，孔隙主要为原始粒间孔及少量粒内溶孔，原始孔隙发育，连通性好，分布均匀；颗粒以直接接触为主，胶结类型以孔隙式胶结为主。该类样品的核磁共振饱和谱以双峰大孔为主，离心前后峰的幅度变化较大，可动峰幅度基本消失，束缚水饱和度分布在9.2%~24.5%之间。该类孔隙结构的储渗性能最好，是主要的产油气层，日产液量一般大于150 t。

(a) 铸体薄片；(b) 核磁共振横向弛豫时间谱

II类孔隙结构的铸体薄片、核磁共振横向弛豫时间谱等实验结果如图7所示。从图7可见：孔隙度分布在15.33%~20.15%之间，平均为17.08%；渗透率分布在10.36×10−3~150.76×10−3μm2之间，平均为48.38×10−3μm2；岩石以细粒为主，分选中等，磨圆度中等(次棱为主，次圆为辅)，泥质含量较低，孔隙以原始粒间孔及少量粒内溶孔为主，但连通性较差；颗粒以直接接触为主，胶结类型以接触式胶结为主。该类孔隙结构的核磁共振饱和谱以双峰为主，离心后可动峰幅度变小，不可动峰幅度基本不变，束缚水饱和度分布在17.68%~50.27%之间。该类孔隙结构的储集性能较好，日产液量一般在20~150 t之间。

(a) 铸体薄片；(b) 核磁共振T2谱

III类孔隙结构的铸体薄片、核磁共振横向弛豫时间谱等实验结果如图8所示。从图8可见：孔隙度分布在10.4%~17.63%之间，平均为13.26%；渗透率分布在1.44×10−3~20.62×10−3μm2之间，平均为8.38×10−3μm2；岩石以细粉粒为主，分选中等，磨圆度中等(次棱为主)，泥质含量较高，孔隙连通性差；颗粒以直接接触为主，胶结类型以接触式胶结为主。核磁共振饱和谱以双峰为主，不可动峰幅度大，束缚水饱和度在26.2%~65.5%之间。该类孔隙结构具一定的储集性能，但渗透性差，非均质性强，日产液量一般在10~20 t之间。

(a) 铸体薄片；(b) 核磁共振共振横向弛豫时间谱

IV类孔隙结构的铸体薄片、核磁共振横向弛豫时间谱等实验结果如图9所示。从图9可见：孔隙度分布在5.4%~11%之间，平均为7.2%；渗透率分布在0.2×10−3~16.3×10−3μm2之间，平均为2.8×10−3μm2；分选差，磨圆度中等(以次棱为主、次圆为辅)，孔隙类型主要为粒间溶孔，孔隙零散分布于颗粒和胶结物间，连通性差，以孔隙式胶结为主。核磁共振饱和谱以不可动峰为主，束缚水饱和度在68.5%~84.6%之间。该类孔隙结构的储渗能力差，自然日产液量一般在2~5 t之间，一般需压裂改造才可能获得较低产能。

(a) 铸体薄片；(b) 核磁共振共振横向弛豫时间谱

V类孔隙结构的铸体薄片、核磁共振横向弛豫时间谱、核磁非均质性系数、毛管压力等实验结果如图10所示。从图10可见：孔隙度分布在0.7%~6.3%之间，平均为3.2%；渗透率分布在0.01×10−3~6.8×10−3μm2之间，平均为0.8×10−3μm2；分选和磨圆度中等(次棱为主)，孔隙类型主要为粒间或粒内溶孔，孔隙发育在颗粒边缘、方解石胶结物的解理缝或长石溶蚀孔(缝)内，连通性差，以孔隙式胶结为主。核磁共振饱和谱以不规则峰为主，束缚水饱和度大于80%。该类孔隙结构储层一般为干层，无开采价值。

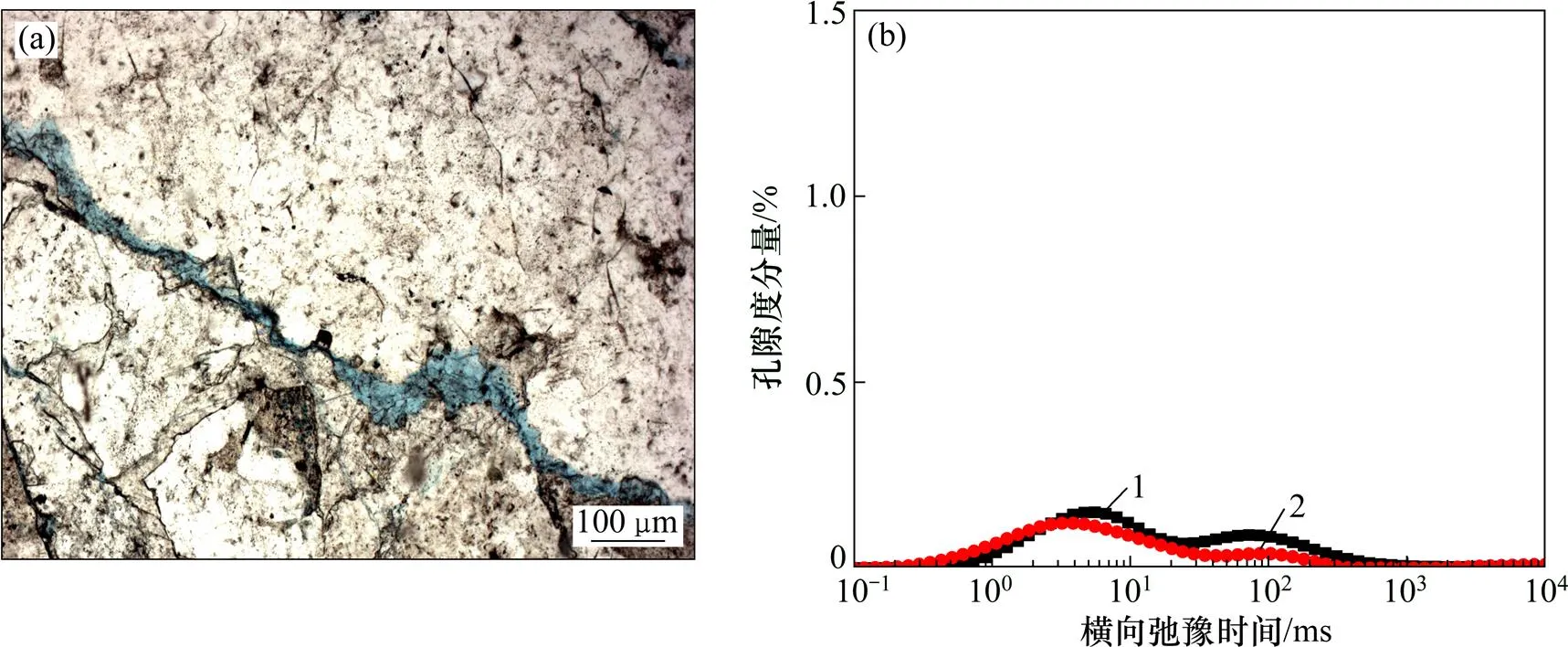
(a) 铸体薄片；(b) 核磁共振共振横向弛豫时间谱

5种孔隙结构的微观特征参数范围及产液能力如表1所示。由表1可知：从I类到V类，孔隙度和渗透率逐渐减小，孔隙的连通性变差，束缚水饱和度增大，非均质性变强，产液能力逐渐变弱，孔隙结构分类结果与试油结果十分吻合，说明算法的有效性。微观特征参数结果表明：形状因子及孔隙半径减小，孔隙纵横比、迂曲度、非均质性系数和分维数增大。

表1 不同孔隙结构类型的微观参数特征

注：(−)/中，表示最小值，表示最大值，表示平均值。

5 结论

1) 谱聚类算法的本质与非均质储层孔隙结构具有一致性，适用于非均质程度高、孔隙结构复杂、常规硬聚类算法难以解决的非线性分类问题，收敛性好。

2) 将信息熵理论应用于谱聚类算法中，避免了尺度参数人为设定对分类结果产生的误差，实现了尺度参数的自动计算，信息熵−谱聚类算法所得孔隙结构分类结果与试油结果具有良好的对应性。

3) 模糊算法的引入有效地解决了样本归属问题。通过最优隶属度准则确定了最佳孔隙结构样本，不同孔隙结构类型的微观参数有所差异，表现为：形状因子及孔隙半径减小，孔隙纵横比、迂曲度、非均质性系数和分维数增大；从I类到V类物性变差，孔隙结构变复杂，非均质性变强。

[1] Dyman T S, Krystinik K B, Takahashi K I. Quantitative Petrographic analysis of mid-cretaceous sandstones, southwestern montana[R]. USA, Denver: U S Geological Survey, 1988: 14−22.

[2] 王本鉴, 王宏. 一种综合分析多种测井信息自动识别储层的方法[J]. 成都地质学院学报, 1990, 17(3): 121−125. WANG Benjian, WANG Hong. A method of automatic reservoir recognition with synthetical analysis of multi-well-logging informations[J]. Journal of Chengdu College of Geology, 1990, 17(3): 121−125.

[3] 刘顺生, 孙丽霞. 用统计学方法研究克拉玛依油田储层分类[J]. 新疆石油地质, 1991, 12(3): 237−242. LIU Shunsheng, SUN Lixia. Application of statistics to the classification of reservoir in karamay oilfields[J]. Xinjiang Petroleum Geology, 1991, 12(3): 237−242.

[4] 姚萌, 徐樟有, 熊琦华, 等. 数理统计分析方法在储层分类中的应用[J]. 石油学报, 1994, 15(增刊): 105−109. YAO Meng, XU Zhangyou, XIONG Qihua, et al. Applying mathematical statistic analysis methods to the classification of reservoir[J]. Acta Petrolei Sinica, 1994, 15(Suppl): 105−109.

[5] 蔡忠, 王伟锋, 金强, 等. 灰色聚类分析再储集层分类评价中的应用[J]. 石油大学学报(自然科学版), 1996, 20(增刊): 16−20. CAI Zhong, WANG Weifeng, JIN Qiang, et al. Application of grey cluster analysis in reservoir classification evaluation[J]. Journal of the University of Petroleum (Edition of Natural Sciences), China, 1996, 20(Suppl): 16−20.

[6] 吴东胜, 郭建华, 吴智勇, 等. 古潜山储层模糊评价方法及其应用[J]. 西南石油学院学报, 2001, 23(3): 5−9. WU Dongsheng, GUO Jianhua,WU Zhiyong, et al. Fuzzy evaluation and application of buried carbonate reservoir[J]. Journal of Southwest Petroleum Institute, 2001, 23(3): 5−9.

[7] 张顶学, 刘新芝, 徐永高, 等. 模糊物元欧氏贴近度分析方法在储层分类中的应用[J]. 石油天然气学报(江汉石油学院学报), 2005, 27(5): 560−562. ZHANG Dingxue, LIU Xinzhi, XU Yonggao, et al. Application of analytical method of fuzzy in reservoir classification[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 2005, 27(5): 560−562.

[8] Dubois M K, Bohling G C, Chakrabarti S. Comparison of rock facies classification using three statistically based classifiers[R]. USA, Kansas: Kansas Geological Survey, 2005: 1−8.

[9] 焦创赟, 付伟, 赵俊兴, 等. 白豹油田长4+5成岩作用与储层分类评价[J]. 成都理工大学学报(自然科学版), 2006, 33(5): 522−527. JIAO Chuangyun, FU Wei, ZHAO Junxing, et al. Diagenesis and reservoir classification and evaluation of Member 4+5 of Triassic Yanchang Formation in Baibao oilfield, Ordos Basin, China[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2006, 33(5): 522−527.

[10] 张晓东, 陈景山. 蜀南气田嘉二段储层分类评价的模糊综合评判[J]. 石油天然气学报(江汉石油学院学报), 2007, 29(1): 59−62. ZHANG Xiaodong, CHEN Jingshan. Integral fuzzy evaluation on jia2 reservoir classification in Jia2 member of Shunan gas field[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 2007, 29(1): 59−62.

[11] Genty C, Jensen J L, Ahr W M. Distinguishing carbonate reservoir pore facies with nuclear magnetic resonance measurements[J]. Natural Resources Research, 2007, 16(1): 45−54.

[12] 杨波, 高清祥, 杨杰. 聚类分析法在城壕油田西259井区长32储层分类评价中的应用[J]. 石油天然气学报(江汉石油学院学报), 2010, 32(6): 22−26. YANG Bo, GAO Qingxiang, YANG Jie. Application of Cluster Analysis in Reservoir Chang32Evaluation of Wellblock Xi259 in Chenghao Oilfield[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 2010, 32(6): 22−26.

[13] Rodolfo S B, Duarry A, Cintia M, et al. How to propagate petrophysical properties in a fracture network for naturally fractured carbonate reservoirs−case study: cretaceous formation at Maracaibo Lake, Venezuela[C]//SPE Europec/Eage Annual Conference and Exhibition. Spain, Barcelona: SPE, 2010: 1−14.

[14] Emad A E, Ognian A, Abdulazeez A, et al. Data mining in identifying carbonate litho-facies from well logs based from extreme learning and support vector machines[C]//AAPG GEO Middle East Geoscience Conference & Exhibition. Bahrain Manama: AAPG, 2010: 1−6.

[15] 何琰. 基于模糊综合评判与层次分析的储层定量评价—以包界地区须家河组为例[J]. 油气地质与采收率, 2011, 18(1): 23−25, 29. HE Yan. A quantitative reservoir evaluation method based on fuzzy comprehensive appraisal and analytical hierarchy process-case of Xujiahe formation, Baojie area[J]. Petroleum Geology and Recovery Efficiency, 2011, 18(1): 23-25, 29.

[16] 王礼常, 王志章, 陶果. 致密砂岩气藏储层分类新方法[J]. 科技导报, 2011, 29(4): 47−49.WANG Lichang, WANG Zhizhang, TAO Guo. A novel classification method for the tight sandstone reservoir[J]. Science & Technology Review, 2011, 29(4): 47−49.

[17] 谭锋奇, 李洪奇, 许长福, 等. 基于聚类分析方法的砾岩油藏储层类型划分[J]. 地球物理学进展, 2012, 27(1): 246−254. TAN Fengqi, LI Hongqi, XU Changfu, et al. Reservoir classification of conglomerate reservoir based on clustering analysis method[J]. Progress in Geophysics, 2012, 27(1): 246−254.

[18] Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm[J]. Pattern Recognition, 2003, 36(2): 451−461.

[19] 王玲, 薄列锋, 焦李成. 密度敏感的半监督谱聚类[J]. 软件学报, 2007, 18(10): 2412−2422.WANG Ling, BO Liefeng, JIAO Licheng. Density-sensitive semi-supervised spectral clustering[J]. Journal of Software, 2007, 18(10): 2412−2422.

[20] 卜德云. 自适应谱聚类算法的研究与应用[D]. 南京:南京航空航天大学信息科学与技术学院, 2010: 2−18. BU Deyun. Research and application on adaptive spectral clustering algorithm[D]. Nanjing:Nanjing University of Aeronautics and Astronautics. College of Information Science and Technology, 2010: 2−18.

[21] 李娟. 改进相似性测度的谱聚类研究[D]. 大连: 大连理工大学管理与经济学部, 2012: 9−40. LI Juan. Research on spectral clustering with improved similarity measure[D]. Dalian: Dalian University of Technology. Faculty of Management and Economics, 2012: 9−40.

[22] 周荫清. 信息理论基础[M]. 北京: 北京航空航天大学出版社, 2006: 20−43. ZHOU Yinqing. Principle of information theory[M]. Beijing: Beihang University Press, 2006: 20−43.

[23] 周燕婷, 黄卓和. 信息和熵[J]. 广州师范学院学报(自然科学版), 1998, 19(7): 78−82. ZHOU Yanting, HUANG Zhuohe. Information and entropy[J]. Journal of Guangzhou Normal University (Nature Science Edition), 1998,19(7): 78−82.

[24] 刘洪林, 朱秋影, 周振兴. 模糊聚类分析及其在测井识别油气层中的应用[J]. 勘探地球物理进展, 2005, 28(6): 425−427. LIU Honglin, ZHU Qiuying, ZHOU Zhenxing. Fuzzy cluster analysis and its application in identification of reservoir bed with logging data[J]. Progress in Exploration Geophysics, 2005, 28(6): 425−427.

[25] 范宜仁, 葛新民, 汪海龙, 等. 非均质砂砾岩储层渗透率预测方法研究[J]. 西南石油大学学报(自然科学版), 2010, 32(3): 6−10. FAN Yiren, GE Xinmin, WANG Hailong, et al. Study on the method predicting permeability in the heterogeneous glutenite reservoir[J]. Journal of Southwest Petroleum University (Science& Technology Edition), 2010, 32(3): 6−10.

(编辑 罗金花)

Pore structure typing of heterogeneous clastic reservoir using information entropy-fuzzy spectral clustering algorithm

GE Xinmin1, 2, FAN Yiren1, 2, TANG Limin3, CHEN Yiguo4, QI Linhai5, XING Shuai6

(1. School of Geosciences in China University of Petroleum, Qingdao 266580, China;2. CNPC Key Well Logging Laboratory in China University of Petroleum, Qingdao 266580, China;3. Down Hole Service Sub-Company of Daqing Oilfield Company, Daqing 163000, China;4. Research Institute of Shanxi Yanchang Petroleum (Group) Co. Ltd., Xi’an 710075, China;5. Hailar Headquaters of Petroleum Exploration and Development of Daqing Oil field Company, Daqing 163000, China;6. Changqing Division, China Petroleum Logging Co. Ltd., Xi’an 710201, China)

A method of automatic typing was proposed by using information entropy-fuzzy spectral clustering algorithm. Complete convergence was obtained by using spectral clustering algorithm to solve the convex distribution clustering problem, thus the ‘dimension disaster’ was avoided effectively. In the light of information entropy theory, the scale parameters of spectral clustering algorithm were optimized and then the types of pore structures were presented. On this basis, in combination with each sample of the pore structure types of membership from fuzzy mathematics algorithm, various types of pore structure of different samples can be obtained according to the membership degree of optimal rule

(membership degree of samples for one pore structure is greater than 70%).The results show that the results of pore structure typing obtained from the algorithm are in good agreement with well test and production test results, and its engineering application effect is very obvious.

heterogeneous clastic reservoir; pore structure typing; fuzzy spectral clustering algorithm; information entropy; scale parameter optimizing

10.11817/j.issn.1672-7207.2015.06.034

P631.8+4

A

1672−7207(2015)06−2227−09

2014−10−10；

2014−12−20

国家自然科学基金资助项目(41404086)；山东省自然科学基金资助项目(ZR2014DQ007)；中国博士后基金资助项目(2014M56059)；国家科技重大专项(2011ZX05020-008)(Project (41404086) supported by the National Natural Science Foundation of China; Project (ZR2014DQ007) supported by the Natural Science Foundation of Shandong Province; Project (2014M56059) supported by the China Postdoctoral Science Foundation, Project (2011ZX05020-008) supported by the Major Project of Science and Technology of China)

葛新民，博士(后)，从事测井储层评价、岩石物理实验及解释方面的研究；E-mail：gexinmin2002@163.com