一种非全相配电网系统的短路电流计算方法

伊丽洁，宋增祥，孙冰莹，李　智，马新勇，梁慧媛

（1.国网山东省电力公司淄博供电公司，山东　淄博　255000；2.国网山东桓台县供电公司，山东　恒台　256400；3.国网山东节能服务有限公司，济南　250001）

一种非全相配电网系统的短路电流计算方法

伊丽洁1，宋增祥1，孙冰莹2，李智1，马新勇1，梁慧媛3

（1.国网山东省电力公司淄博供电公司，山东淄博255000；2.国网山东桓台县供电公司，山东恒台256400；3.国网山东节能服务有限公司，济南250001）

非全相配电网短路电流的快速准确计算一直是一个难题。基于传统的对称分量法，提出一种改进算法，即引入虚拟节点和虚拟线路阻抗来计算非全相配电网系统故障时的短路电流。与传统的短路电流计算方法相比，该算法大大提高了短路电流计算的效率，并可更直观地对配电网系统中的复杂故障情况进行分析。

非全相配电网络；短路电流计算；对称分量法；虚拟节点法

0　引言

在区域配电网络中，电气设备和载流导体的选择、限制短路电流措施的确定、继电保护及自动装置的整定都需要进行短路电流计算。在电力系统非全相的配电网络运行过程中，短路故障快速计算、分析的问题显得更为困难和突出。已有的短路故障分析计算方法中，利用MATLAB等仿真软件对配电网系统建立电磁暂态模型并进行短路故障仿真计算的方法虽然较为精确，但计算量较大且模型化实现较为困难，不适合实际工程使用［1］。而对称分量法是一种常用的对“对称系统不对称运行状态”进行分析、计算的算法［2］。

对称分量法在对称三相交流系统中不对称故障下的电气计算分析上已有广泛的应用，但对于非全相配电网络发生故障时的短路电流计算问题无法应用［3］。对此，提出一种适应性广且易于仿真建模的短路水平分析计算方法，即利用虚拟节点补全不对称输电网络，简化并扩展传统对称分量法的应用范围。对于复杂配电网系统的不对称短路故障分析具有重要意义。

1　虚拟节点法原理

虚拟节点的序分量计算方法如图1所示，将单相或双相地线路添加虚拟节点和虚拟线路补全成为完整的三相输电线路。由于虚拟节点之间并没有实际的电压和电流存在，故虚拟阻抗取得任意值都可满足欧姆定律，且由于没有电流产生的互感，故虚拟线路并没有相间阻抗的存在［4-5］。可以将新的节点矩阵视为一个相间阻抗为零，虚拟相阻抗为任意值的新的阻抗矩阵并由对称分量法来进行短路电流的计算和分析。

图1　虚拟节点的序分量计算方法

2　虚拟节点法

2.1虚拟节点法的计算流程

虚拟节点法短路电流计算流程如图2所示。

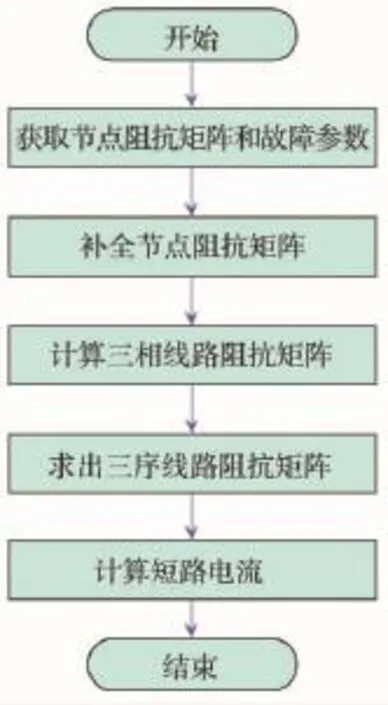
图2　虚拟节点法短路电流计算流程

第一步：输入节点阻抗矩阵；

第二步：由于虚拟节点和线路中并没有实际电流通过，故取任意值都不会违反欧姆定律，所以虚拟阻抗取已知节点阻抗的平均值，虚拟线路的相间阻抗为零；

第三步：计算三相线阻矩阵，线路阻抗是由故障点位置占线路长度百分比除以基础线路阻抗再乘以节点阻抗矩阵得到

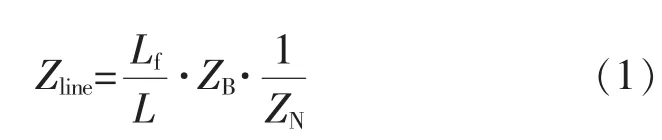
式中：Lf为故障点位置；L为线路长度；ZB为节点阻抗矩阵；ZN为线路基础阻抗。

第四步：由三个不对称相量与三组对称相量之间的关系求出三序线阻矩阵；

第五步：由三序线路阻抗矩阵求短路电流。

2.2虚拟阻抗矩阵

如图1，在主线k，l之间只有c相实际存在，假设存在虚拟的节点ab和虚拟阻抗ZddkL，因为虚拟阻抗并不存在，所以线路上并没有加载负荷，流入虚拟线路的电流为零，故线路虚拟阻抗ZddkL设为任何值都不会违背欧姆定律。为了方便计算，线路虚拟阻抗ZddkL设为ZcckL，故线路阻抗矩阵就变为

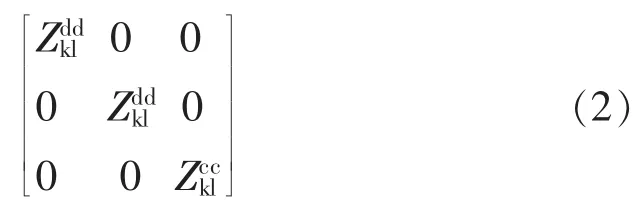
2.3计算方法的选择

在实际配电网络发生故障后，进行快速短路电流计算时，通过对输入阻抗矩阵进行分析，如果是单相输电，即只存在一条输电线路，输入节点阻抗矩阵是一维的，而双相输电则为二维阻抗矩阵。由此可以基于输入矩阵维数对输电方式进行推测分析并加以补全，如图3所示。

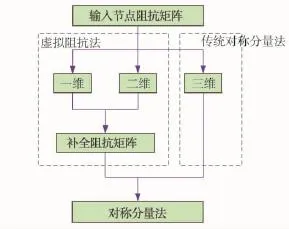
图3　计算方法自动选择流程

3　配电网中的短路电流计算方法

3.1运算曲线法

虚拟节点法实质是对对称分量法无法计算部分的补充，使得对称分量的计算方法在单相和双相的输电线路中仍然可用，与传统的对称分量法的主要区别在于将不存在的节点和线路用遵循欧姆定律的虚拟阻抗来代替，这种计算方法扩大了传统对称分量法的计算使用范围［6］。

在计算电力网络的短路电流时，根据我国的电机参数实例，国内一般常用运算曲线法［7］。具体的算法为：规定发电机的X″d为等值电抗，不考虑电力网络中负荷参量，从而得到等值网络，再通过网络化简，得到仅包含发电机电动势节点和短路故障节点的简化网络模型。简化网络模型中所有的阻抗值均为按最初确定的功率基准值计算得到的，因此各电源与短路点间的转移阻抗可以分别归算到不同电源的额定容量中，以此可得到计算电抗，查阅计算电抗运算曲线，便可得到任意时刻的短路电流标幺值。

运算曲线法的基本步骤。

1）忽略负荷，画等值电路，发电机以次暂态电抗代表；

2）任取功率基准值SB，同时取各级电压基准值为UB=Uav，计算各参数值；

3）网络模型化简：依据电源类型、与短路点之间的电气距离，可以划分得到若干组电源，再将每组电源等值成一个等效电源，从而求出各组电源至短路点的转移电抗Xki；

4）将Xki归算成对应于各等效电源容量下的计算电抗Xjsi；

5）查阅短路电流运算曲线，求出t时刻各等效电源贡献的短路电流周期分量标幺值Ii*；

6）计算各电源对短路点的短路电流的有名值

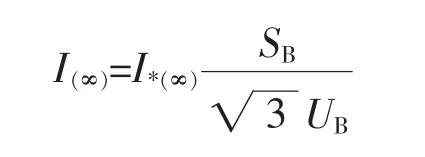
7）短路点总的短路电流

It= I1+ I2+ …+ I（∞）

在电力网络实际计算中，网络的情况多种多样，不同发电机的暂态过程参数曲线与变化规律也不一致。因此，为了准确、快速地进行短路电流计算，可以将具有相近短路电流曲线的发电机合并，对于特殊的发电机，再单独计算考虑。上述计算思想即是：将网络中的多个电源划分成若干电源组，每组电源均使用唯一的等值电源代替，这就是个别变化计算法［8］。

3.2元件更替法

为保证电力系统稳定，需要进行三类计算：潮流计算、故障分析计算、稳定分析计算。结合运算曲线法的计算思路与输电网络分层分区的网络特性，提出一种新的分层分区短路电流计算模型：元件更替法。元件更替法将电网模型视为各种点和线的连接，并引用矩阵计算网架元件的短路电流值，如图4所示。

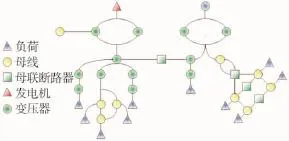
图4　等效的元件更替法模型

元件更替法算法步骤。

1）将无限大的电力系统简化为有限大电力系统，只保留需要“单独计算”的特殊电源；

2）计算短路点的附加阻抗；

3）计算单个电源对短路点贡献的正序电流，根据零序电流值对应表，即可求取相应的负序、零序电流值；

4）重复上述步骤2～3，逐个计算各电源提供的各序短路电流；

5）得到短路点各序电流；

6）基于节点阻抗方程，进一步求解其它电气量［9］。

4　算例对比与分析

MATLAB的电力系统模块库（Power System Block Set）可以进行复杂电力系统的建模和稳态、暂态计算。使用IEEE-13节点多相电机测试模型进行仿真计算，见图5。

故障位置为607，查询IEEE 13 node test feeder可知，故障线路长度为0.244 km；线路基础阻抗为173.06 Ω；单相线阻阻抗为（1.4925+0.6231）Ω；线路总长度1.61 km。故障类型由图可以看出是单相接地，可以增加虚拟节点和虚拟线路将其补全成为三相接地输电电路。故有：

其中，矩阵中第二行和第三行的阻抗是由单相阻抗推出的虚拟阻抗的值，且由于其余两相均为虚拟线路，故没有相间阻抗存在。

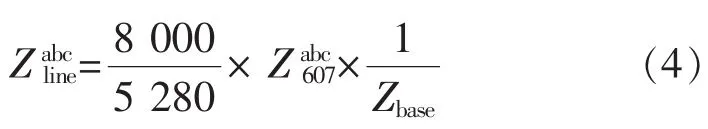
由式（4）得：

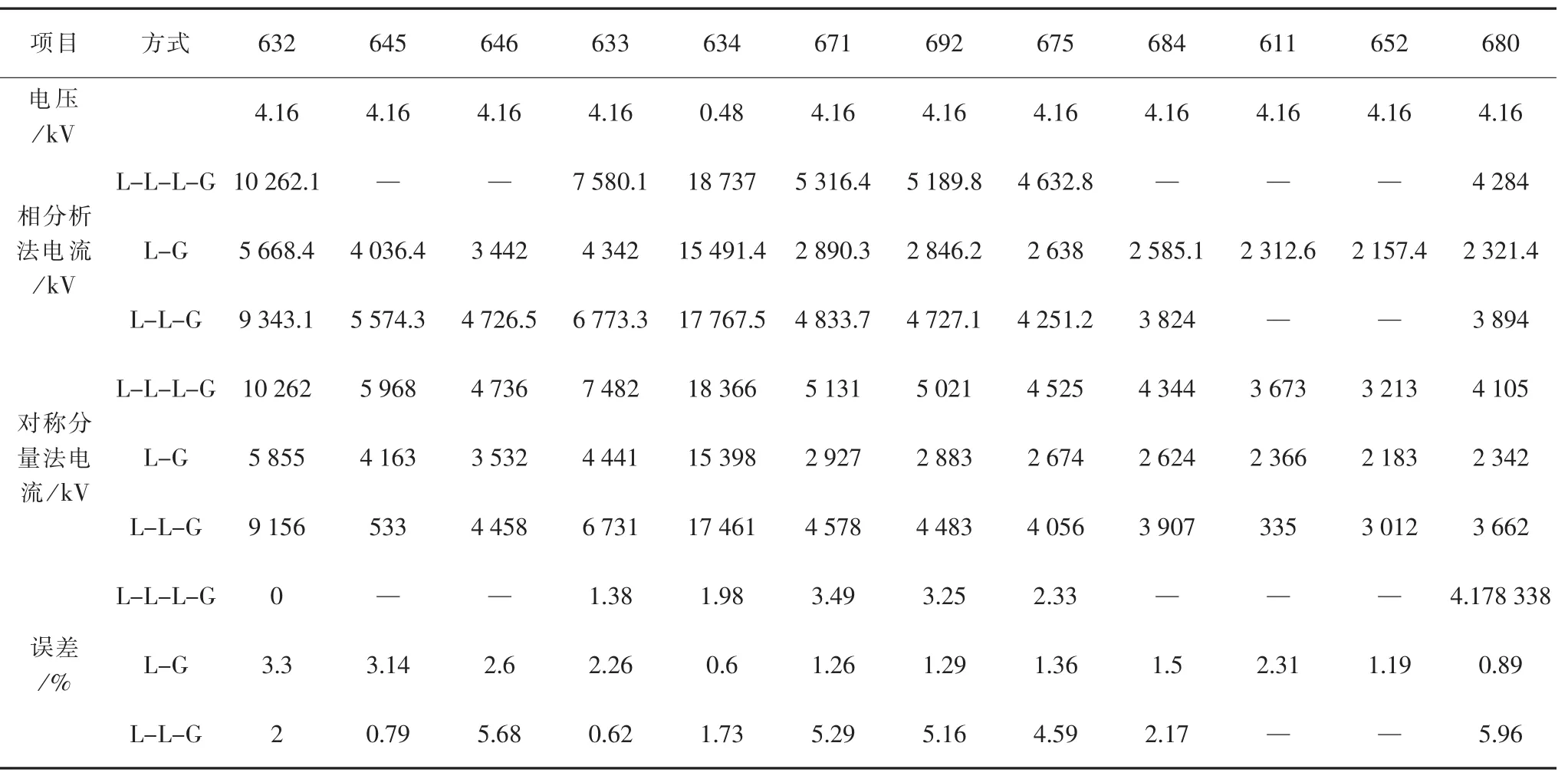
表1　故障电流分析表

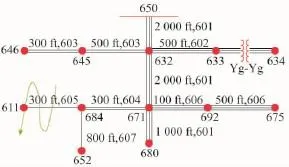
图5　IEEE-13节点多相电机测试模型

式（5）将节点阻抗矩阵转化成为线路阻抗矩阵，即将阻抗矩阵由单纯的体现节点属性的阻抗矩阵转化为可用于计算的含有长度和基础线阻的线路属性的阻抗矩阵。将代入可求出短路电流。计算得Iseq=2 183 A与真实结果Iph=2 312.6 A的结果误差率为为2.31%，满足工程误差要求。

表1展示了基于传统算法和新算法的短路电流分析对比，结果表明两者非常相近，最大误差出现于三相输电线路的680节点，为5.96%，误差产生的主要原因是两相输电线路之间的线路耦合感应。由于短路电流的计算主要目的是求短路电流水平，只要短路电流的数量级相近即可满足工程需求，故该算法满足要求。

5　结语

随着特高压受端电网的不断扩大，电网分区运行是目前发展的必然趋势，短路电流问题将由原来的主网大短路电流的计算转移为越来越多的分区电网短路电流计算，快速准确的短路电流水平计算为电网短路电流控制设备的选择提供可靠依据。本文针对传统算法在适应性和算法实现困难的问题，对传统的对称分量法进行了改进和优化，提出一种更适用于复杂配电网系统的不对称短路故障分析方法，可以对短路电流水平进行快速、准确的计算，为受端电网的网架规划和设备方案选择提供参考。

［1］Mamdouh Abdel-Akher and Khalid Mohamed.“Fault Analysis of MultiphaseDistributionSystemsUsingSymmetricalComponents，”IEEE Transactions onPowerDelivery，Vol.25，Issue. 4，2010，pp.2 931-2 939.

［2］W.H.Kersting，“Distribution System Modeling and Analysis.Boca Raton，”Vol.3，No.5，2002，pp.269-299.

［3］John H B，Klaus J F.Elimination of transformer inrush current by controlled switching″partⅠ：theoretical consideration.IEEE Transactions on Power Delivery，Vol.16，No.2，2001，pp.276-280.

［4］John H B，Klaus J F.Elimination of transformer Inrush current by controlled switching″partⅡ：application and performance considerations.IEEE Transactions on Power Deliver，2001，Vol.16，No.2，pp.281-285.

［5］M.Young.The Technical Writer's Handbook.Mill Valley，CA：Uni versity Science，1989.

［6］M.E.Baran and I.El-Markaby.“Fault analysis on distribution feeders with distributed generators，”IEEE Trans.Power Syst.，Vol.20，No.4，2005，pp.1 757-1 764.

［7］T.N.Boutsika and S.A.Papathanassiou.“Short-circuit calculations in networks with distributed generation，”Elect.Power Syst.Res.，vol.78，No.7，2008，pp.1 181-1 191.

［8］R.K.Gajbhiye，B.Gopi.P.Kulkarni，and S.A.Soman.“Computationally ef cient methodology for analysis of faulted power systems with series-compensated transmission lines：A phase coordinate approach，”IEEE Trans.Power Del.，Vol.23，No.2，2008，pp.873-880.

［9］M.Abdel-Akher，K.M.Nor，and A.H.Abdul-Rashid.“Improved three-phase power-ow methods using sequence components，”IEEE Trans.Power Syst.，Vol.20，No.3，2005，pp.1 389-1 397.

A Calculation Method of Short Circuit Current in Open-phase Distribution Power System

YI Lijie1，SONG Zengxiang1，SUN Bingying2，LI Zhi1，MA Xinyong1，LIANG Huiyuan3
（1.State Grid Zibo Power Supply Company，Zibo 255000，China；2.State Grid Huantai Power Supply Company，Hengtai256400，China；3.State Grid Shandong Energy-saving Co.，Ltd.，Jinan 250001，China）

It is always difficult to fast and accurately calculate short circuit current of an open-phase network.Based on the conventional symmetrical component method，an improved method is proposed，in which virtual node and line impedance are introduced.Compared with the conventional method，calculation efficiency of the improved method is highly promoted.Also，the complicated fault of open-phase network can be analyzed more intuitively.

open-phase distribution network；short circuit current calculation；symmetrical component method；virtual node method

TM713

A

1007-9904（2015）09-0028-04

2015-05-13

伊丽洁（1972），女，高级工程师，从事电力营销工作。