投影梯度法模糊层次综合评价模型在饱和负荷分析中的应用

高　崇，唐　潇，左郑敏，朱向前，欧阳旭，姚建刚

（1.广东电网发展研究院有限责任公司，广州　510080；2.湖南大学 电气与信息工程学院，长沙　410082）

投影梯度法模糊层次综合评价模型在饱和负荷分析中的应用

高崇1，唐潇2，左郑敏1，朱向前2，欧阳旭2，姚建刚2

（1.广东电网发展研究院有限责任公司，广州510080；2.湖南大学 电气与信息工程学院，长沙410082）

饱和负荷是体现一个城市负荷发展最终规模的重要指标，研究城市饱和负荷的规模对于城市电力工业的规划和发展，特别是城市电网的建设和改造具有重要的指导意义：饱和负荷作为远期电网规划的重要依据，可以确定地区电网应有的最大供电能力［1］；以远期规划为依据指导近期电网规划建设，避免频繁的改扩建工程和土地、人力、材料等资源浪费，提高城市电网建设资金使用率，促使电网规划、建设与城市规划、建设相适应［1，2］；可以确定负荷分布情况，结合城市总体规划，规划变电站布点和线路走廊，有利于促进城市电网建设与城市发展的相互协调［3］。

1　研究现状

近年来，众多学者对饱和负荷预测进行了深入研究，提出了人口容量特征参数类比法、饱和负荷密度特征参数类比法、饱和负荷空间分布预测法等预测方法［4］。而这些方法的参数确定要类比同类型城市的发展，根据人为主观经验获得，带有较强的主观因素，影响到预测准确性。

有学者已将模糊综合评价模型运用到利克特量表的心理测量数据评价分析、物流配送中心选址优劣问题、高职教学评价问题、建设项目多方案决策问题、科技人才创新能力评价［5—9］等方面。也有学者将模糊评价法运用到电力负荷水平评价上［10］，但其通过德尔菲法获得评价指标的权重，具有较强的人为主观因素，不能准确地反映评价指标的影响程度。

本文将基于投影梯度法的模糊层次综合评价模型对城市饱和负荷水平进行综合评价，通过投影梯度法改进各项评价指标权重的获取方法，把判断矩阵的一致性检验与权值计算结合起来，利用一致性指标函数?值最小化来推求权值，在评价因素确定的情况下，通过调整判断矩阵各影响因素标度来改进一致性指标值，优化各影响因素的权重，实际计算中，因为这是一类“主动”方法，计算权值误差小，计算稳定性强［11］，克服了权重计算时主观性较强的缺陷，提高了评价的合理性，为各个预测算法的参数选取提供客观依据，提高预测算法的精度。

2　基于投影梯度法的模糊层次综合评价模型

步骤1：构建模糊评价矩阵A（r（i，j））n×n。

（1）确定评价因素集：Y=（y1，y2，…，yi，…，ym），其中yi表示评价因素。

（2）确定评价语集R=（r1，r2，…，ri，…，rn）

（3）确定模糊评价矩阵

其中（ai1，ai2，…，aij，…，ain）中的aij表示评价因素yi在评语等级ri上的隶属函数，其值等于评价因素yi被评为等级ri的人数占总人数的比例。

A满足下列条件

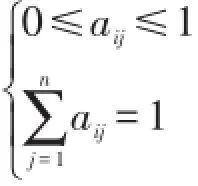
步骤2：建立评价因素集（y1，y2，…，yi，…，ym）的判断矩阵C。

采用层次分析法中的1～9间的整数及其倒数作为标度来构造各评价因素间的两两比较判断矩阵C，比例的标度及其含义见表1。

表1　比例标度及其含义

步骤3：评价因素的权重计算。

设C各评价因素（y1，y2，…，yi，…，ym）的单排序权

m值为ωk，k=1～m，且满足ωk＞0和∑k=1ωk=1。根据判断矩阵C的定义，理论上有

这时矩阵B具有如下性质：①cij=ci/cj=1/cji；②cii=ωi/ωi=1；③cijcjk=（ωi/ωj）（ωj/ωk）=cik。

其中，称性质①为判断矩阵的倒数性；②为判断矩阵的单位性；称性质③为判断矩阵的一致性条件，它表示相互关系可以定量传递。性质③也是性质①和性质②的充分条件。

现在的问题就是已知判断矩阵C来推求各评价因素的单排序权值｛ωk|k=1～m｝。若判断矩阵C满足式（1），决策者能精确度量ωi/ωj，即cij=ωi/ωj（i，j=1～m），判断矩阵C具有完全的一致性，于是有

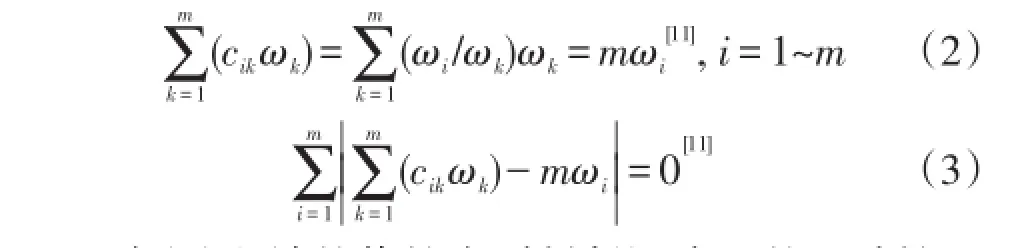
式（3）左端的值越小则判断矩阵C的一致性程度就越高，当式（3）成立时判断矩阵C具有完全的一致性，基于此C的各评价因素的单排序及其一致性检验问题可以归结为如下优化问题

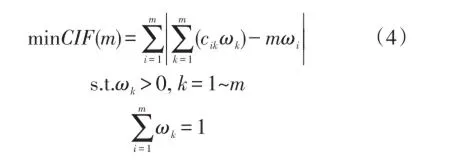
式中：minCIF（m）为简化的一致性指标函数，单排序权值ωk（k=1～m）为优化变量，当判断矩阵B具有完全的一致性时，式（1）成立，从而式（4）取全局最小值CIF（m）=0，又根据约束条件∑i=1ωk=1知，该全局最小值是唯一的［11］。

文献［7］—文献［9］和文献［11］中一致性指标函数是非线性约束问题。遗传算法广泛运用于复杂的全局最优化问题，它既不要求目标函数就有特定性质，也不要求可行域具有好的结构，在解决许多复杂的非线性约束问题上具有明显优势［12］。式（4）是一种线性约束问题，运用传统的投影梯度法解决带有线性不等式约束和线性等式约束的最优化问题，有精确的可行解搜索方向，较遗传算法有计算过程简便、收敛快、结果更准确的优点。

该算法从初始可行解ωk0（k=1～m）开始，在确定的可行下降方向上进行精确的线性搜索，寻找更优的可行解，当CIF（m）值小于某一标准值时，可认为判断矩阵C具有满意的一致性，据此计算的各评价因素的权值ωk是可接受的，否则就需要反复调整判断矩阵C各评价因素的标度cij，直到CIF（m）比标准值小，判断矩阵具有满意的一致性为止。

步骤4：计算评价因素的评价向量B

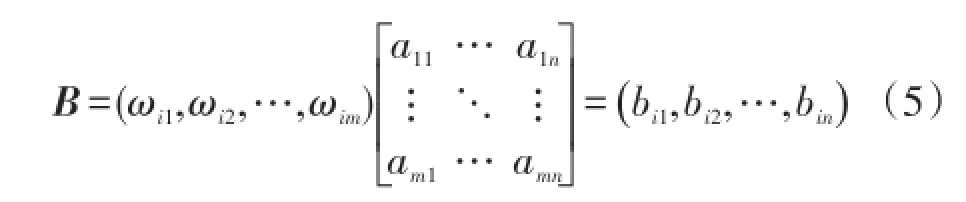
因此B=（bi1，bi2，…，bin）是评价指标评价得分向量。

3　城市饱和负荷水平的评价指标体系

3.1经济因素对城市饱和负荷的影响

在经济迅速发展时期，某一地区的电力需求最直接的反映便是地区的电力负荷，因此经济增长和产业结构对地区的负荷发展有着深刻的影响。

第二产业发展占主导地位的发展中城市，经济发展速度快，电力需求大，负荷增长速度快。当城市发展趋近饱和时，电力负荷增长缓慢，电力负荷饱和水平高。第三产业占主导地位新型工业城市，城市发展速度快，但第三产业产值单耗较低，因此电力需求较少，该城市电力负荷发展到饱和状态时，负荷饱和水平较低。

3.2社会因素对城市饱和负荷的影响

城市人口规模、地区政策、科技发展水平等社会因素对负荷的发展有着重大影响。

人口规模是影响城市电负荷的重要因素之一，在城市经济水平和产业结构相近的城市，人口规模越大，全社会用电量越大，电力负荷饱和水平越高。

国家政策也是城市发展重要影响因素，经济特区政策为该城市的发展提供各项政策性的倾斜，经济发展迅速，在饱和经济态势下需要大量的电力供应，所以饱和负荷水平高。

3.3自然因素对城市饱和负荷的影响

自然因素中，主要有气候、地形等因素对城市的电力负荷影响较大。

平原地区的地势平阔，交通便利，大量人口聚集，城市经济发展速度较快，负荷增长迅速，饱和负荷水平高。高原山地地势高低起伏，交通不便，工业生产和商业发展受限，电力水平低，饱和负荷水平低。

城市气候影响主要体现在高温、严寒等极端气候地区，城市人口较少，电力负荷密度小，电力负荷饱和水平低。

本文从经济因素、自然因素、社会因素3方面来评价城市电力负荷饱和水平，建立饱和负荷评价指标体系，详细见表2。

表2　饱和负荷评价指标体系

此评价体系可以根据城市的实际发展情况，依据对电力负荷影响大小程度对指标体系进行补充和完善，以使指标体系符合当地电力负荷发展的实际情况。

4　算例分析

4.1所选地区概况

S市作为省会城市，是综合性强的国际性大都市，地处中南部，是典型的港口沿海城市。

4.2电力负荷饱和程度分析评价

4.2.1指标选取

根据S市概况以及参考S市2000年至2013年的各项经济指标如表3所示。

本文选取评价语系V=（v1，v2，…，vi，…，vn）=｛饱和

｝水平高，饱和水平中，饱和水平低 ，参考S市年鉴及相关资料，根据S市实际发展情况，结合20位专家的意见，对表3的S市的各项指标进行深入分析，得到如表4所示的评价体系。

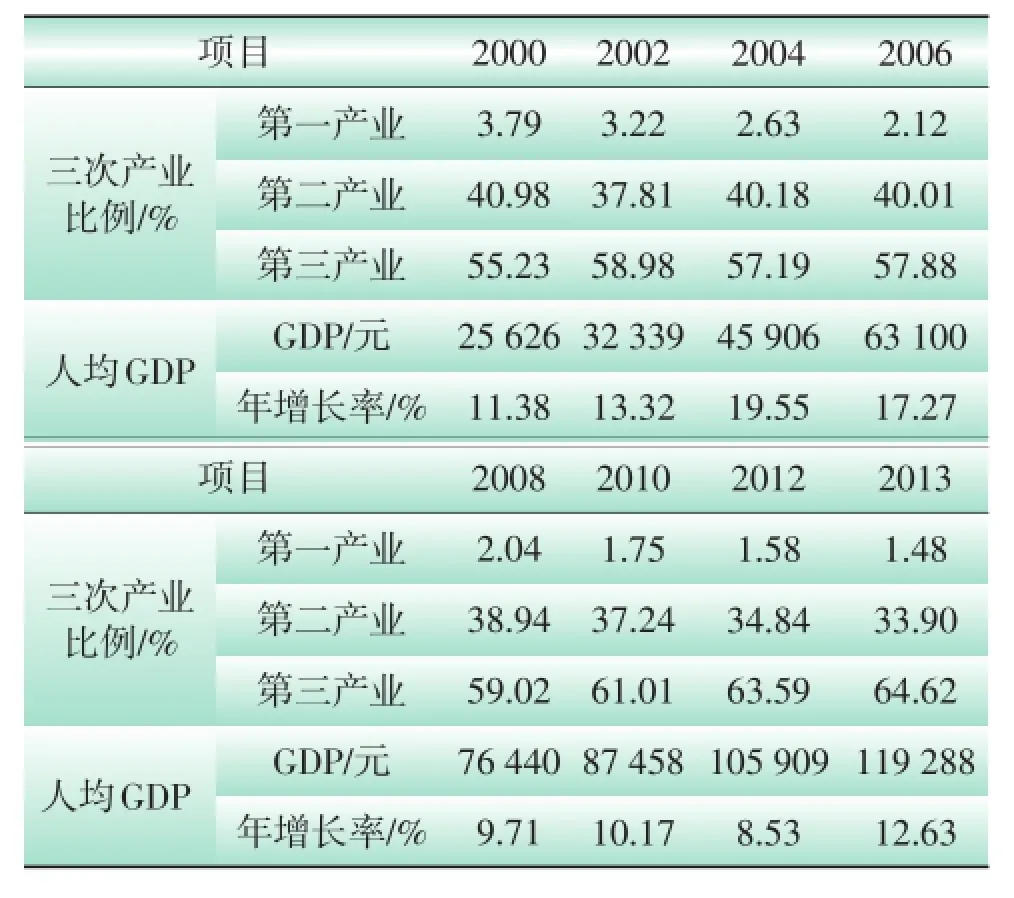
表3　2000年至2013年各项经济指标

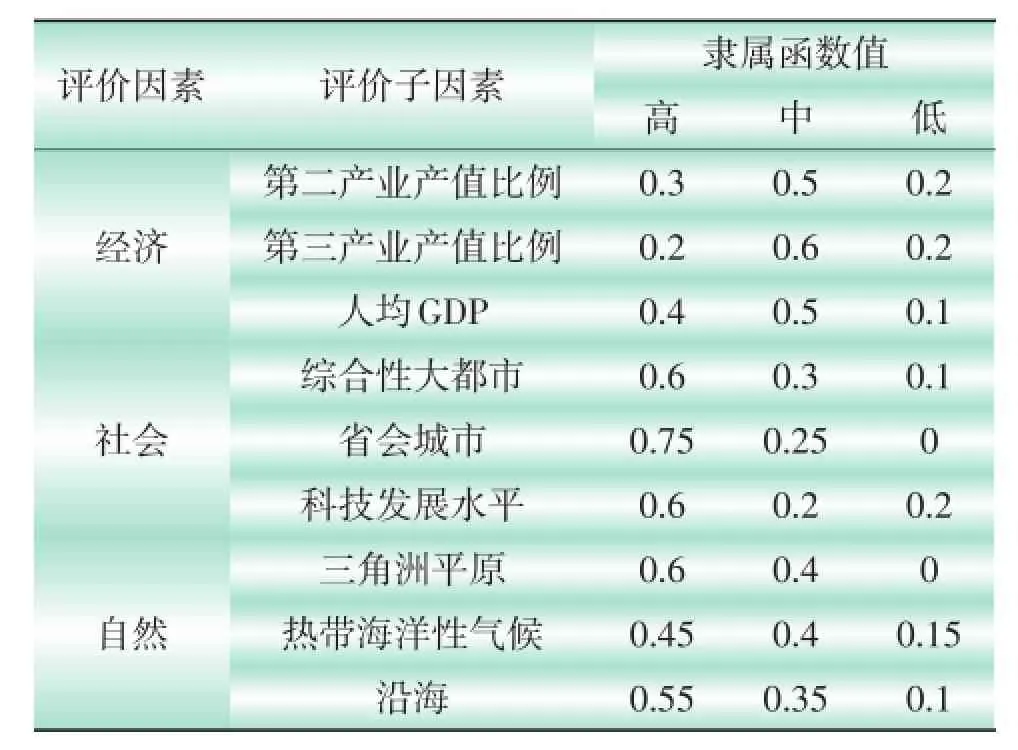
表4 评价指标体系

S市的第三产业产值比例大于第二产业产值比例，呈快速上升趋势，说明该市第三产业行业在该市占主导地位，第三产业发展需求较第二产业大，但仍有较大的发展空间。因此，第三产业产值比例饱和水平偏于中等水平，且低于第二产业产值比例饱和水平。人均GDP年增长率保持在10%以上，饱和水平偏向于中等水平。其他指标的隶属函数值的确定，则是根据实际可知事实而定。从以上分析可得到如4表各指标的隶属函数值。

由表4分析情况可得经济因素、社会因素、自然因素的模糊评价矩阵

4.2.2计算权重

按照模型中的步骤2，得出子因素之间的两两比较表，建立判断矩阵C1、C2、C3。根据步骤3计算各评价子因素的权重。如表5、表6、表7所示。

表5　经济因素子因素两两比较表

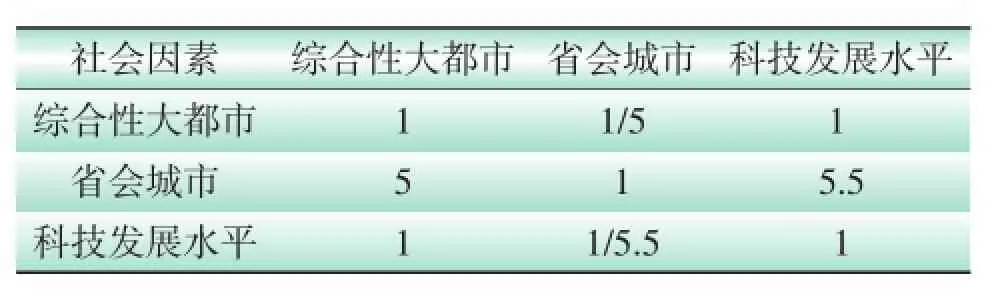
表6　社会因素子因素两两比较表

表7　自然因素子因素两两比较表

由此可得出判断矩阵C1、C2、C3

根据式（4），利用投影梯度法对判断矩阵C1、C2、C3进行一致性检验和权重计算，结果如表8所示。

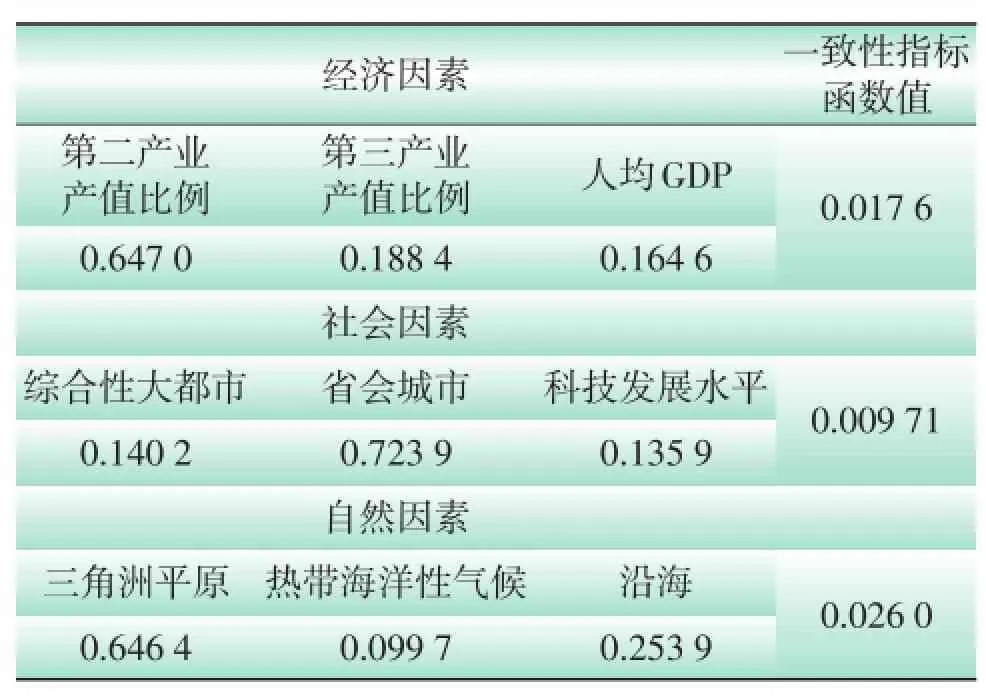
表8　权重及一致性指标函数值

表8中的各评价因素的一致性指标函数值小于0.03，满足要求，则3类子因素权重向量为：w1=｛0.647 0 0.188 4 0.164 6｝；w2=｛0.140 2 0.723 9 0.135 9｝；w3=｛0.646 4 0.099 7 0.253 9｝。

同理，根据可确定经济因素、社会因素、自然因素的判断矩阵C4

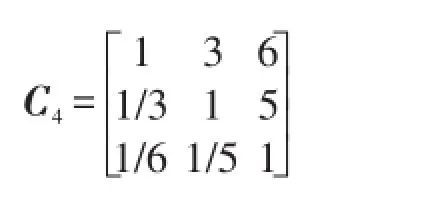
由C4得出3个因素权重分别为：w4=｛0.129 7 0.732 40.137 9｝。一致性指标函数值为：0.003 6。经济因素评价向量

B1=w1A1=｛0.297 6 0.518 9 0.183 5｝（6）社会因素评价向量

B2=w2A2=｛0.708 6 0.250 2 0.041 2｝（7）自然因素评价向量

B3=w3A3=｛0.572 3 0.387 3 0.040 4｝（8）则电力负荷饱和程度的综合评价向量为

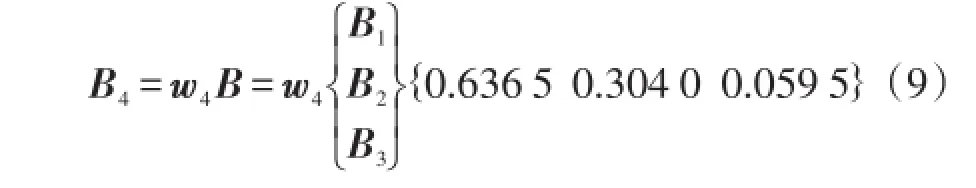
式（9）表明，S市电力负荷饱和程度高、中、低所占的比重为63.65%、30.40%、5.95%。根据最大隶属度原则，未来该市电力负荷属于高饱和水平区。

5　结束语

本文提出了基于投影梯度法的模糊层次综合评价法模型，根据地区电力负荷发展的实际情况建立了合适的评价体系，得到了合理的模糊评价矩阵和判断矩阵，根据判断矩阵建立一致性指标函数，运用了投影梯度法计算一致性指标函数最小值，将判断矩阵的一致性检验和评价因素权重计算同时进行，当判断矩阵一致性满足要求时得到的权重更符合实际情况。

用某城市作为算例，对该市电力负荷饱和水平进行分析评价，评价结果负荷当地实际发展情况，验证了此方法的合理有效性，为城市饱和负荷预测提供有效借鉴。D

［1］ 崔凯，李敬如，刘海波，等.城市负荷饱和阶段电力规划方法及其在济南电网中的应用［J］.电网技术.2007，31（S2）：131-134.

［2］ 崔凯，李敬如，赵彪，等.城市饱和负荷及其预测方法研究［J］.电力技术经济，2008，20（6）：34-38.

［3］ 肖峻，杜柏均，耿芳.城市电力负荷饱和分析方法［J］.电力科学与技术学报，2009，24（4）：54-58.

［4］ 江新琴，李喜兰.基于空间饱和负荷密度的城市远景饱和负荷预测［J］.福州大学学报：自然科学版，2008，36（4）：532-536.

［5］ 余嘉元.基于遗传算法的模糊综合评价在心理测量中的应用［J］.心理学报，2009，41（10）：1 015-1 023.

［6］ 任春玉，王晓博.基于遗传算法和模糊综合评价法物流配送中心选址研究［J］.物流科技，2006，24（10）：78-81.

［7］ 葛琳.基于遗传算法的模糊层次综合评判在高职教学评价中的应用［D］.广州：广州大学，2011.

［8］ 冯晖.遗传算法结合模糊综合评价在建设方案决策中的应用［D］.合肥：合肥工业大学，2006.

［9］ 刘泽双，章丹，康英.基于遗传算法的模糊综合评价法在科技人才创新能力评价中的应用［J］.西安理工大学学报，2008，24（3）：376-381.

［10］ 王芳东，林韩，温步瀛，等.基于模糊综合评价法的电力负荷饱和程度分析［J］.电力与电工，2010，30（3）：1-3.

［11］ 金菊良，魏一鸣，付强，等.计算层次分析法中排序权值的加速遗传算法［J］.系统工程理论与实践，2002，22（11）：39-43.

［12］ 李董辉，童小娇，万中.数值最优化［M］.北京：北京出版社，2000.

The application of fuzzy hierarchy comprehensive evaluation model based on projection gradient method in analysis for electric load saturation

GAO Chong1，TANG Xiao2，ZUO Zheng⁃Min1，ZHU Xiang⁃qian2，OUYANG Xu2，YAO Jian⁃gang2
（1.Guangdong Power Grid Development Research Institute Co.，Ltd.，Guangzhou 510080，China；2.College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

提出了基于投影梯度法的模糊层次综合评价模型，对城市饱和负荷水平进行客观评价。根据评价指标体系，创建了判断矩阵和一致性指标函数。利用投影梯度法计算一致性指标函数最小值，检验、修正判断矩阵的一致性。通过调整判断矩阵的各评价因素标度改进了一致性指标值，优化了各评价因素的权重。计算结果表明：此算法是一类“主动”方法，计算权值误差小，计算稳定性强，克服了权重计算时主观性较强的缺陷，提高了评价结果的合理性。同时，以某市电网为研究对象，从社会因素、自然因素、经济因素3个方面，评价了该市负荷饱和水平，评价结果合理有效，具有良好的参考作用。

饱和负荷；投影梯度法；模糊层次综合评价模型；一致性指标函数；判断矩阵

The fuzzy hierarchy comprehensive evaluation mod⁃el based on projection gradient method was created to objectively an⁃alyze the level of electric load saturation.Based on evaluation index system，judgment matrix and consistency index function were creat⁃ed.The projection gradient method was used to calculate the mini⁃mum value of consistency index function which aimed at testing and modifying the consistency of the judgment matrix.The consistency in⁃dex value and the weight of each influencing factors were optimized by adjusting scales of evaluation factors in judgment matrix.The re⁃sult shows that this method is an active method with strong stability and minor error in calculating weight.The method also overcomes ob⁃jective weakness in calculating weight and improves the rationality of the evaluation result.Meanwhile，a city was taken as the researching object and this city's load saturation level was evaluated from social factors，natural factors and economic factors.The result is reasonable and effective with a good reference.

saturation load；projection gradient method；fuzzy hierarchy comprehensive evaluation；consistency index function；judgment matrix

TM714

B

2015-03-23；

2015-06-03

高崇（1983），男，吉林双阳人，高级工程师，硕士，研究方向为电力系统规划；唐潇（1988），男，湖南长沙人，硕士研究生，研究方向为负荷预测；左郑敏（1976），女，广东顺德人，高级工程师，硕士，研究方向为电力系统规划；欧阳旭（1988），男，湖北武汉人，博士研究生，研究方向为负荷预测；朱向前（1981），男，河南西华人，讲师，博士，研究方向为负荷预测；姚建刚（1952），男，湖南长沙人，教授，研究方向为电力市场、电网规划、高压绝缘子等。