多元回归与年龄移算法在老龄人口研究中的整合分析
吴启凡
(河海大学公共管理学院,南京211100)
多元回归与年龄移算法在老龄人口研究中的整合分析
吴启凡
(河海大学公共管理学院,南京211100)
我国人口老龄化问题日趋明显,现阶段对人口老龄化的模型研究依然存在问题,在对我国人口老龄化情况的研究过程中,单纯运用多元回归的方法需考虑多重共线性问题,为避免此问题则要优选变量,但在逐步回归过程中又会将对其可能造成显著性影响的偏相关扰动项忽略,而且单纯运用回归模型进行预测将在长时间序列中造成较大误差,为此,结合年龄移算法对回归因子进行单项细度预测,再运用回归方程进行宏观计算,将大幅提高预测的精度。本文以男性人口、女性人口、城市人口、乡村人口等因素进行动态研究,先根据相关性分析,初步筛选影响因素,再通过多元线性回归找到人口老龄化与人口结构中相关因素的数量关系,这里通过逐步回归出恰好出现了偏相关扰动项无法接受检验的情况,我们运用两种标准化方法结合Mann-Whitney U检验进行验证分析,最终运用年龄移算模型和回归矩阵预测人口老龄化发展趋势,并根据预测结果进行相关分析,给出相应评价。
多元线性回归;Mann-Whitney U检验;年龄移算模型
一、回归因子优选
对于人口老龄化问题,我们需要将男性人口数、女性人口数、城市人口数、乡村人口数、少年儿童人口数(小于14周岁)、青壮年人口数(15-64周岁)作为我国人口结构中对人口老龄化有影响的几个因素[1],考虑到计划生育政策从1981年正式施行,我们选择1982年开始的数据进行统计,由于前十年内计划生育政策刚刚进入初期阶段,对人口老龄化的影响并不明显,我们在初期前十年,以五年为单位进行研究,以减小运算量,从1990年开始以一年为单位进行研究,以加大精确度。统计数据如下:
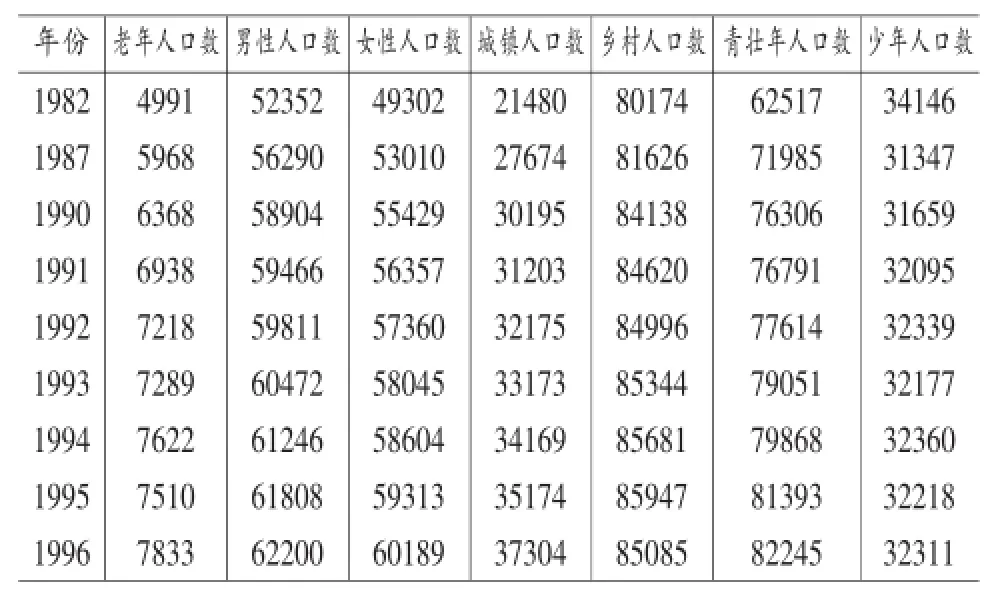
表1 我国1982—2013年人口统计数据(单位:万人)
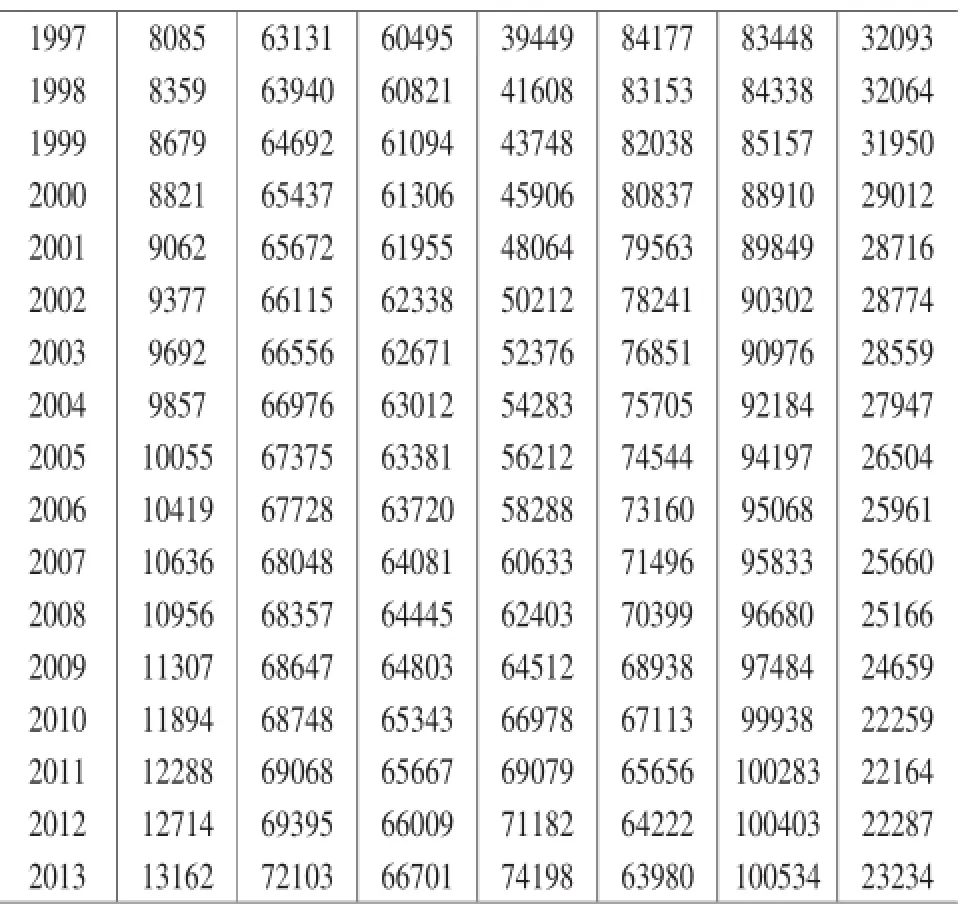
1997 8085 63131 60495 39449 84177 83448 32093 1998 8359 63940 60821 41608 83153 84338 32064 1999 8679 64692 61094 43748 82038 85157 31950 2000 8821 65437 61306 45906 80837 88910 29012 2001 9062 65672 61955 48064 79563 89849 28716 2002 9377 66115 62338 50212 78241 90302 28774 2003 9692 66556 62671 52376 76851 90976 28559 2004 9857 66976 63012 54283 75705 92184 27947 2005 10055 67375 63381 56212 74544 94197 26504 2006 10419 67728 63720 58288 73160 95068 25961 2007 10636 68048 64081 60633 71496 95833 25660 2008 10956 68357 64445 62403 70399 96680 25166 2009 11307 68647 64803 64512 68938 97484 24659 2010 11894 68748 65343 66978 67113 99938 22259 2011 12288 69068 65667 69079 65656 100283 22164 2012 12714 69395 66009 71182 64222 100403 22287 2013 13162 72103 66701 74198 63980 100534 23234
以上影响因素中部分因素对人口老龄化的影响可能微乎其微,甚至不存在相关关系,为便于分析,我们运用SPSS对上述参数进行分析,结果如下:

表2 正向相关性分析
由上表可以发现男性人口数、女性人口数、城市人口数、乡村人口数、少年儿童人口数(小于14周岁)、青壮年人口数(15-64周岁)等因素均与老龄化人口数存在显著相关关系,并且严格满足置信度99%要求。
二、多元线性回归分析
1.回归分析
由以上分析我们可以对男性人口数、女性人口数、城市人口数、乡村人口数、少年儿童人口数(小于14周岁)、青壮年人口数(15-64周岁)等因素进行多元线性回归[2],但是,在以上参数中,少年人口数与青壮年人口数是我国人口总数与老龄化人口数的差值,具有直接线性关系,会对其他影响因素造成绝对影响,为此,在线性回归过程中,不考虑这两个影响因素,以将其他回归因子的回归系数放大,便于后期对人口老龄化发展情况的预测。
因此,我们只需对男性人口数、女性人口数、城市人口数、乡村人口数进行回归分析,初次回归分析结果如下:
有上表分析可知,城镇人口数与老龄化人口数并不具有回归关系,而男性人口数、女性人口数、城市人口数与人口老龄化具有显著线性相关关系,并且t值较大,sig值均小于0.05,说明回归分析准确可靠,可不进行多重线性回归分析。(对于这种城镇人口数拒绝原假设,乡村人口数接受原假设的情况,我们下面会有进一步分析),由以上回归分析数据我们可以得到回归方程如下:
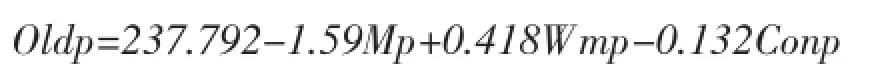
其中:Oldp:老龄化人口数(65岁以上人口数);Mp:男性人口数;Wmp:女性人口数;Cityp:城市人口数;Conp:乡村人口数;Youngp:少年人口数(14岁以下人口数);Midp:中年人口数(15-64岁人口数);
据以上回归方程分析,我们发现男性人口数与女性人口数对人口老龄化的贡献呈负相关关系,这符合男女总体为一的样本规律[3],而城镇人口数不影响老龄化,乡村人口数影响老龄化,这不符合城乡人口总体为一的样本规律 (在研究全国范围内人口问题时可忽略国内人口流动数[4],同时国际人口流动数量级相当小也可忽略不计)[5]。所以我们需要进一步对城市、乡村人口情况与老龄化人口数关系进行进一步分析,作为对比分析,我们采用反向线性回归的方法,由于城、乡人口数不能同时作为因变量来作为自变量的一次函数,我们需要做反向联合分析,这里“城乡人口比”可作为一般参数而不需要进行聚类分析(降维)[6],但是城乡人口比与老龄化人口数不具有相同量纲,我们需对老龄化人口数进行标准化处理,这里我们选用两种标准化方法(即:Min-max标准化方法和z-score标准化方法),以作为对比。
2.z-score标准化法
我们假定原始数据为x,经过z-score标准化处理后的数据为x′,本方法的处理原理就是x经过原始数据的均值和标准差的标准化处理之后,成为量纲为1的x′。
这种标准化方法对于其数据的最大值和最小值都不难以得出的情况尤为适用,同时,如果有个别离散数据超出取值范围时,也可选用此标准化方法。
经过标准化处理后的数据,其变化范围以零为原点波动,比零大证明其比平均水平要高,比零小则比平均水平低。
3.Min-max标准化法
极大、极小值标准化法主要用于对数据进行线性转化。目的是把初始数据x通过极大、极小值标准化后投影到区间[0,1]内得到x′,其公式为:
标准化处理结果如表4。
运用Mann-Whitney U检验方法选出最优标准化方法:如果两个样本数据分别源于两个除均值之外其他参数均相同的总体,那么该两样本选用Mann-Whitney U检验方法,其作用是检验这两个总体的均值差异是否显著[7]。其基本方法是:将两组数据共同排序,从最小的开始作为等级一,依次类推(如果量数据相同,那么取其平均值作为等级选定参数)。之后计算出两个样本的级别W1和W2。
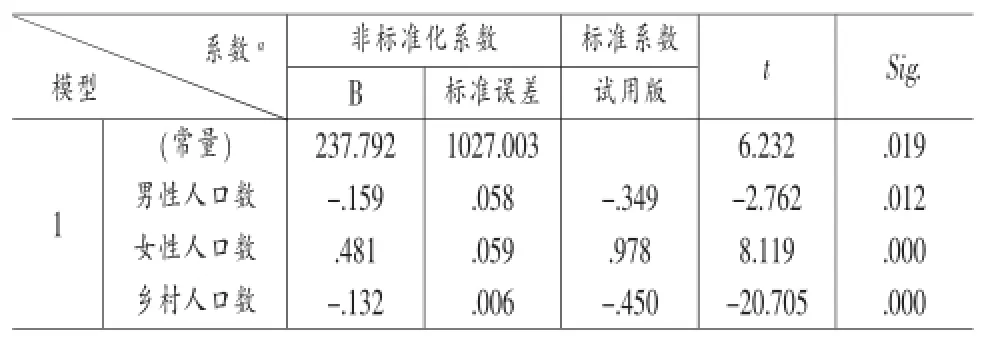
表3 回归分析
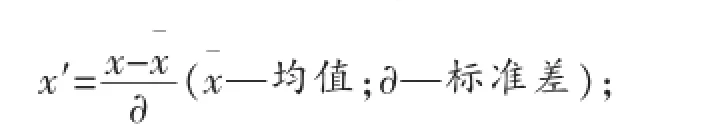

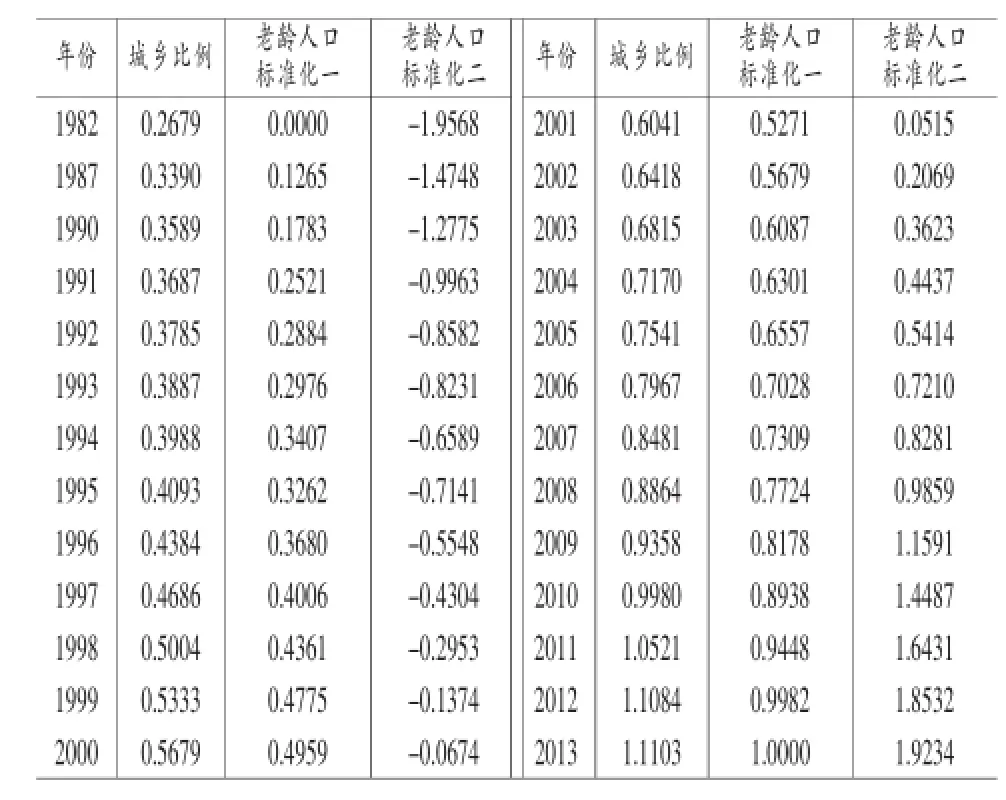
表4 标准化处理结果
计算Mann-Whitney U检验统计量,为第一个样本的量,为第二个样本的量:
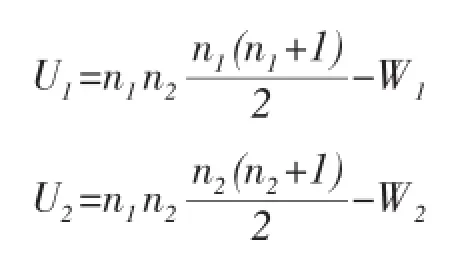
在以上计算结果中,选出较小值Umin与临界值Ua进行比较 (已经整理成为Mann-Whitney U检验的临界值表),如果U<Ua,则其拒绝H0,接受H1。
在原假设为真的情况下,U的均值和分别为:
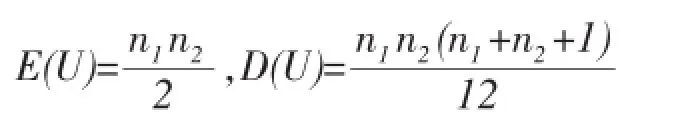
如果n1和n2都不小于10,那么可以确定随机变量近似服从正态分布。设第一个总体的均值为μ1,第二个总体的均值为μ2,则:
(1)H0:μ1≤μ2,H1:μ1>μ2,如果Z<-Za,则拒绝H0;
(2)H0:μ1≥μ2,H1:μ1<μ2,如果Z>Za,则拒绝H0;
(3)H0:μ1=μ2,H1:μ1≠μ2,如果Z<-(Za/2),则拒绝H0;
Mann-Whitney U检验结果如下:
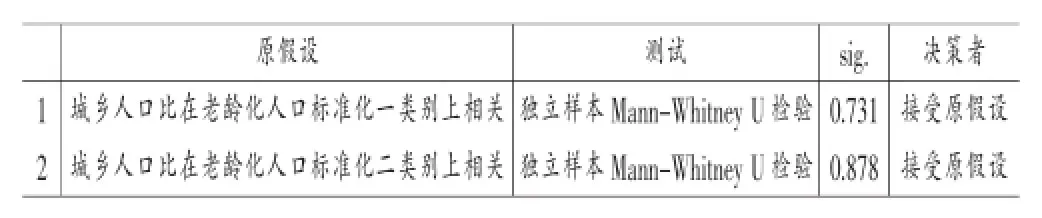
表5 Mann-Whitney U检验
从上表结果中可以看出,第一种标准化方法得的Sig大于0.05,接受原假设;第二种标准化方法得的Sig也大于0.05,也接受原假设,说明两种标准化处理后的数据均可靠。因此我们可以得出结论,无论是单独考虑乡村人口对老龄化的影响,还是综合考虑城乡人口比对老龄化人口的影响[8],都可以得到相应代数关系,也就是说,在不考虑城市人口影响下单纯考虑乡村人口对老龄化的影响也是合理的,为此我们可以证明上述回归方程是正确的。那么在一个长时间序列中,人口老龄化是如何发展的,我们仍需结合其回归方程中的每一个影响因素进行分别预测计算[9],我们选用年龄移算法进行分析计算。
三、年龄移算法
这里我们采用年龄移算法对男性人口数、女性人口数、乡村人口数分别进行预测,然后根据多元线性回归方程计算老龄化人口数量、研究发展趋势,最终得到老龄化人口预测曲线,以便于我国应对老龄化问题采取战略手段。
年龄移算法是由低年龄段人数基于不同年龄段的人口的存活率,来推算下一时间段高年龄段人数的方法。即:在已知第n年人口数量时,可以推算第n+1年的人口数。但是在这个年龄变化的过程中会存在部分人群死亡的情况,所以,第n+1年龄段人口数为第n年龄段人口数乘以(100%-死亡率)。这种逐年移算的方法,称为“年龄移算法”[10]。
同时在计算过程中还应注意的是:计算死亡人口时还应该包括出生人口的死亡。即:
新生人口死亡人数=新生婴儿总数×新生人口的死亡率
按年龄移算法计算年的“新生人口组”人数,应该选用如下公式:
年底“新生人口组”人数=出生人数-死亡人数
第n+1年的人口总数分为两部分来考虑。即
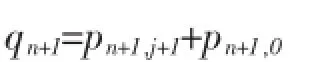
根据年龄推移算法,第n年年底各年龄人口数到第n+1年年底依次转为高一年的年龄组人口,则:
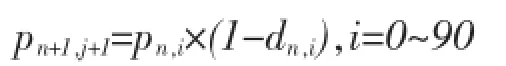
第n+1年0岁的人口数量为 (大于90岁的人口并入90+的人口):
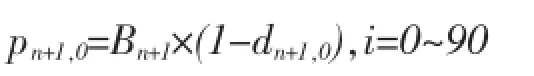
其中,Bn+1为第n+1年出生的人口数,dn+1,0为第n+1年0岁人口的死亡率,人口预测的数学公式和出生人口数的计算公式:
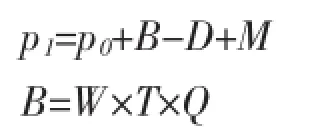
其中,p1为某年年底人数,p0为年初(即上年年底)人数,或为预测开始时调查得到的人数;B为本年出生人数、D为本年死亡人数、M为本年净迁入人口(即迁入人口与迁出人口之差)。B为出生人口数,W为育龄妇女数,T为育龄妇女总和生育率(TFR),Q为育龄妇女生育意愿倾向。
综上所述,以男性人口推算方法为例,建立数学模型如下:
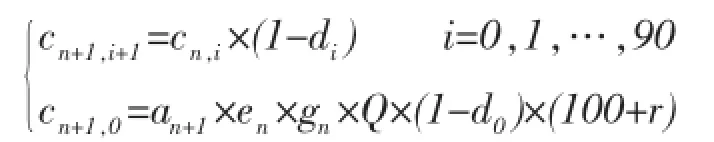
对于其他的各类人口类型同样可得模型预测[11]。
最终我们根据老龄化人口回归方程得矩阵:
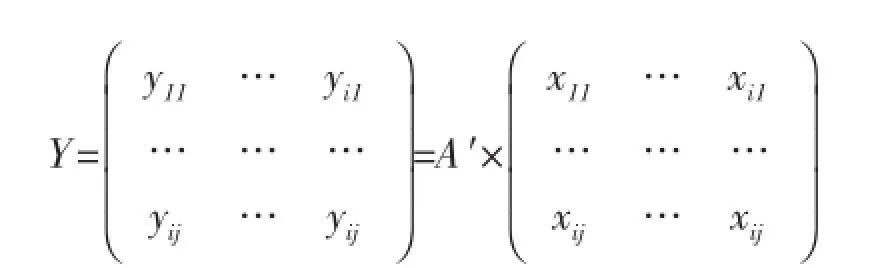
其中,pn,i:第 n年 i岁人口的数量(i=0,1,…,90);di:i岁人口的死亡率(i=0,1,…,90);Bn:第n年出生的人口数;qn:第n年总的人口数;
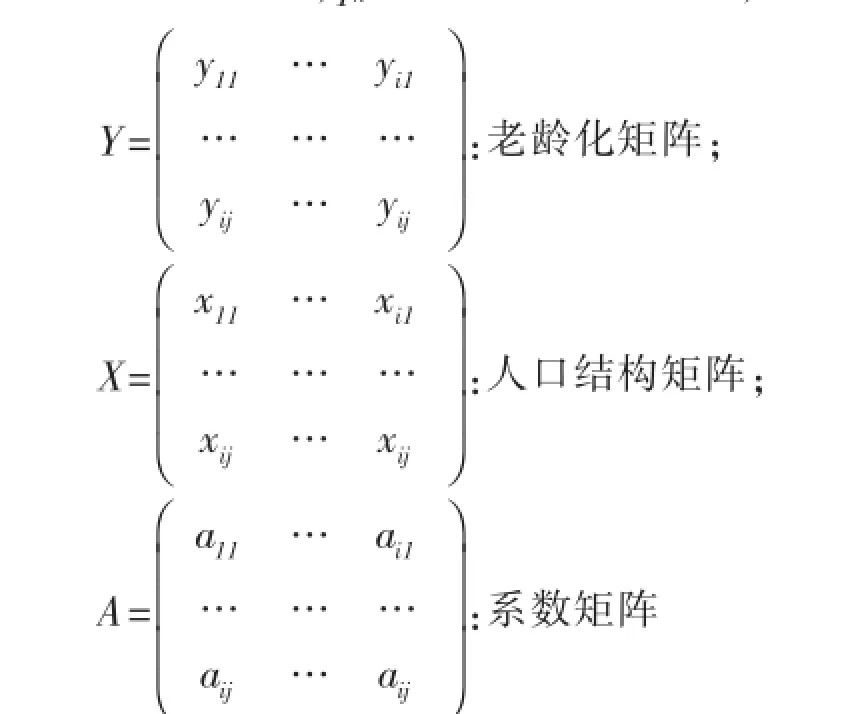
将上述年龄移算法计算得到的男性人口数、女性人口数、乡村人口数预测值带入上述矩阵可得到老龄化人口预测结果如下:
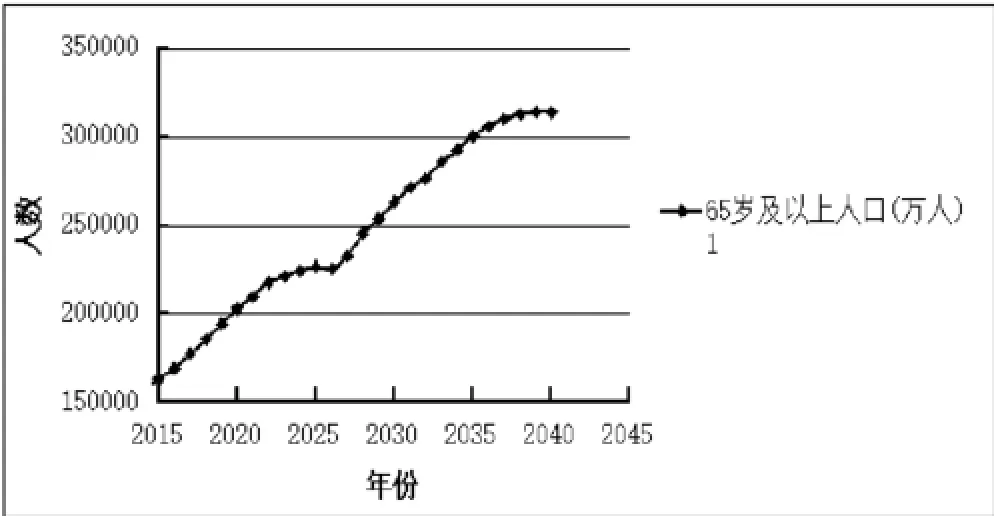
图1 老龄化人口数预测曲线(单位:103人)
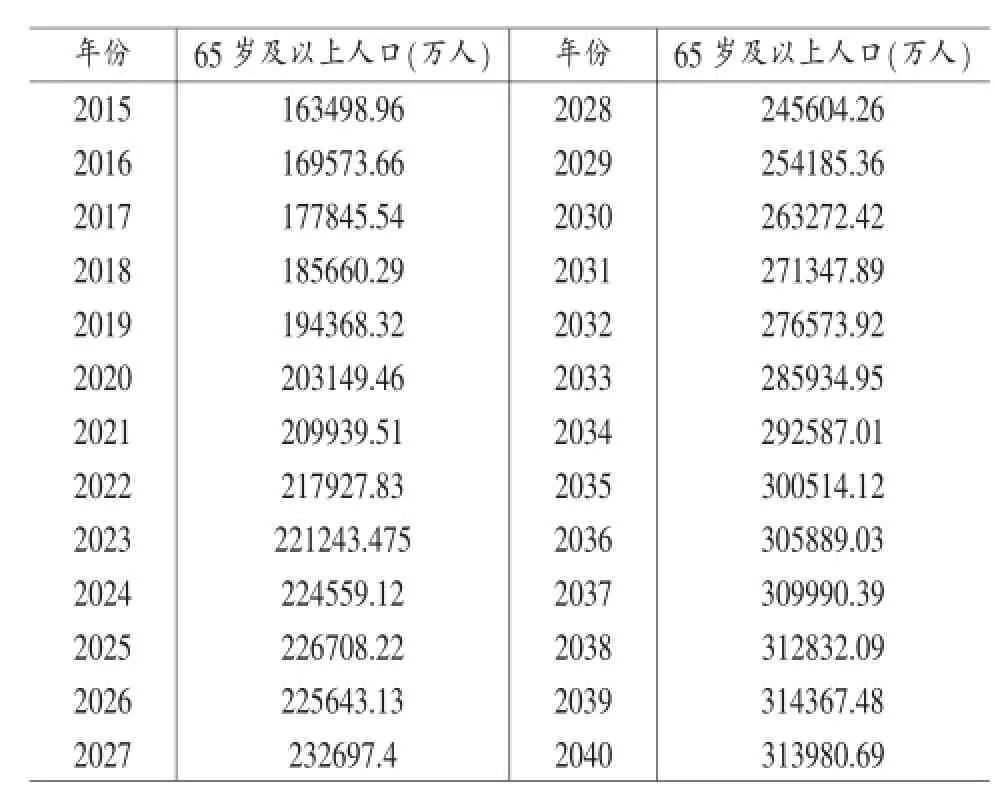
表6 老龄化人口数预测结果(单位:万人)
由以上数据可绘制老龄化人口预测如图1。
由图1观察可以发现,2015—2025年我国老龄化人口处于增加速度缓慢上涨上升趋势,在这里我们需要突出说明一下,在2025年附近出现平缓台阶,据分析,2025年的老龄化人口为65岁以上,其出生年龄约为1960年,而1959年到1961年正是我国三年自然灾害阶段,人口出生率大大减少,所以65年后该年龄段人口数量的增长速度骤降,老龄人口数出现缓阶被很好地反映出来[12],在这种通过年龄移算法与多元线性回归结合的方法中,通过对每一个变量以年龄变化、出生率、死亡率等因素作为计算要素,以一个前沿较长的时间序列为背景很好地预测出了人口老龄化的发展趋势以及实际走势,并可证实本模型的正确性。对于老龄化人口而言,其受到多因素影响,同时对于我国而言,人口基数大,并且长期实施计划生育战略,这样一来对于老龄化人口的研究就尤为困难,而采用多元回归与年龄移算法相结合就很好地解决了回归方法无法对单一变量进行细致计算,年龄移算法无法对宏观变量影响因素分析的弊端,通过模型的互补很好地刻画了我国人口老龄化的发展趋势。值得我们注意的是,虽然人口老龄化速度将在十年后得到改善,但是老龄化人口将具有较大基数,同时我们发现在未来25年里,老龄人口将达到峰值,约3.2亿人,这将对我国经济发展和社会可持续发展造成严重影响,为此,必须采取相应战略措施,让该老龄人口峰值提前到来,并处于较低水平。
[1]陈红敬,饶克勤,钱军程.澳大利亚应对人口老龄化的社会支持体系分析[J].老龄科学研究,2014,2(5):74.
[2]徐辉,吉飞.人口红利,人口年龄结构与中国人口老龄化[J].生态经济,2014,30(3):16-20. [3]张则方.我国出生人口性别比的分析与思考[D].南京理工大学,2008:25-29.
[4]毛蒋兴,王辛宇,郑雄彬等.新型城镇化背景下人口老龄化的城乡规划转型应对[J].规划师,2014(8):18.
[5]易成栋,张纯,吴淑萍等.2000-2010年北京市老年人口空间分布及其变动研究[J].城市发展研究,2014,21(2):66-71.
[6]李芳,李志宏.人口老龄化对城乡统筹发展的影响与对策探析[J].西北人口,2014,35(2):26-30.
[7]卢霞,张恒,陈兴源.人口老龄化发展现状及应对措施研究[J].重庆大学学报(社会科学版),2014,20(2).
[8]蒋诗泉.基于灰色理论的人口老龄化发展趋势及其影响因素研究[J].华东师范大学学报(哲学社会科学版),2014(3).
[9]茆长宝,程琳.两种人口预测模型的精确度比较——以人口年龄移算法和灰色预测模型为例[J].南京人口管理干部学院学报,2009(1):29-32.
[10]陈光慧,蔡远飞,李凤.我国人口老龄化趋势预测与结构分析——基于非参数自回归模型[J].西北人口,2014,35(4):81-87.
[11]谢明柱,査奇芬.基于改进的GM(1,1)模型的我国农村人口老龄化预测[J].江苏农业科学,2014,42(1):399-401.
[12]路锦非,王桂新.国未来城镇人口规模及人口结构变动预测[J].西北人口,2010(4):1-6.
The Meta-analysis of Multiple Regression and Age Shifting Algorithm in the Aging Population Research
WU Qi-fan
(School of public administration,Hohai university,Nanjing 211100)
The problem of our aging population has become more evident,the model for the study of population aging is still a problem at this stage.In the case of China’s aging population of the study,the issues of using a simple method(multiple regression multicollinearity)is to be considered,To avoid this problem may lead to the Multicollinearity,however they will be the likely cause of a significant impact which can be easily ignored.And use the simple regression model to predict the result in the long sequence may also give rise to more errors,so we need to combined with age-shift algorithm to return the individual factors fineness forecast,then use the macro regression equation to calculate,which will significantly improve the prediction accuracy.In this paper,According to correlation analysis,initial screening factors from the male population,the female population,urban population,rural population dynamics.Then find the relationship between population aging and population structure of the related factors by multivariate linear regression.We use two kinds of standardized methods combined with Mann-Whitney U test to make the confirmatory analysis.Finaliy use the age shift operator model and regression matrix to predict the development trend of population aging,and give the analysis and evaluation by the forcasting results.
Multiple linear regression;Mann-Whitney U test;Age shift operator model
C921.2
A
1007-0672(2015)04-0006-05
2014-12-05
江苏人口老龄化对经济社会发展影响及其对策研究,江苏省高校哲学社会科学基金重大项目(项目编号:2010ZDAXM004);社会养老服务体制机制创新研究——基于江苏苏南、苏中、苏北的调查与比较,教育部规划基金项目(批准号:13YJA840008)。
吴启凡,男,黑龙江哈尔滨人,河海大学公共管理学院硕士,研究方向:移民学、人口学、土地资源管理。

