基于分布式压缩感知的宽带协作频谱感知
苏一栋,达新宇
基于分布式压缩感知的宽带协作频谱感知
苏一栋,达新宇
(空军工程大学信息与导航学院,陕西西安,710077)
根据分布式压缩感知理论,提出一种宽带协作频谱感知的方式。该方式相比于以往的协作压缩频谱感知方式,认知用户传向融合中心的数据精简为压缩信号,各个压缩信号在融合中心进行融合重构,这样就减少传向融合中心的数据量,缓解融合中心的数据压力,并且可以提高信号重构的成功率。同时,根据压缩抽样匹配追踪算法,提出一种联合压缩抽样匹配追踪算法。该算法思想是通过加权融合测量样本、迭代重构原信号,以恢复共同的频谱支撑集,完成协作频谱感知。仿真结果表明:与经典的DCS-SOMP算法相比,本文算法性能更优,所需的滤波器数更少。
分布式压缩感知;协作频谱感知;认知无线电
美国联邦通信委员会定义:认知无线电是认知用户(SU)可以不断地执行频谱感知,动态地识别未使用频谱,在保证授权用户(PU)频谱使用的同时,动态高效地使用整个频段[1]。因此,对于认知无线电网络,一个首要的任务就是快速准确地感知整个频段,即宽带频谱感知。但是,需要感知的频谱宽度可能达到几百MHz至几GHz,这样的ADC器件是难以实现的。而压缩感知(CS)技术[2]的出现为宽带频谱感知提供了新的思路。CS理论指出,可以用1个适当的观测矩阵,将1个稀疏的高维信号投影到1个低维空间上,然后通过求解1个优化问题重构原信号。Tian等[3]首先在宽带频谱感知中引入CS理论,其利用模拟/信息转换器(AIC)对接收信号进行亚奈奎斯特采样,然后进行信号重构,最后对频谱占用情况进行判决。同时,由于无线信道衰落,包括阴影效应、多径效应,使得单个SU无法准确地感知频带使用情况,而协作频谱感知利用多个SU的空间分集,可以有效地提高检测性能。曾凡仔等[4]提出了一种分布式宽带压缩频谱感知算法,将获取的SU频谱信息进行加权平均,并作为恢复频谱优化时的约束,降低了计算开销,加速了算法的收敛。顾彬等[5]利用亚奈奎斯特采样值与信道能量之间的关系,提出了一种不需要重构宽带频谱本身,而是直接重构各信道能量的集中式宽带压缩频谱感知算法。无论是集中式还是分布式协作频谱感知,这两篇文献中SU传递的协作信息均为重构的离散的接收信号或其变化形式,传送的数据量过大,而且本地SU还需要消耗一定的计算资源来进行信号重构。为此,本文作者假设短暂的宽带协作频谱感知的整个过程中频谱支撑集不变,由各个SU将数据量相对更少的亚奈奎斯特采样值传递给融合中心FC,FC再利用本文提出的联合压缩抽样匹配追踪算法—SCoSaMP (Simultaneous compressive sampling matching pursuit),对信号进行重构。
1 系统模型及问题的提出
考虑集中式协作频谱感知,如图1所示。假设在总频带宽度为的认知无线电网络中,共有个认知用户SU来感知正在通信的授权用户PU。每个授权用户的通信带宽为,则SU需要对总带宽中的=/个子信道进行感知。
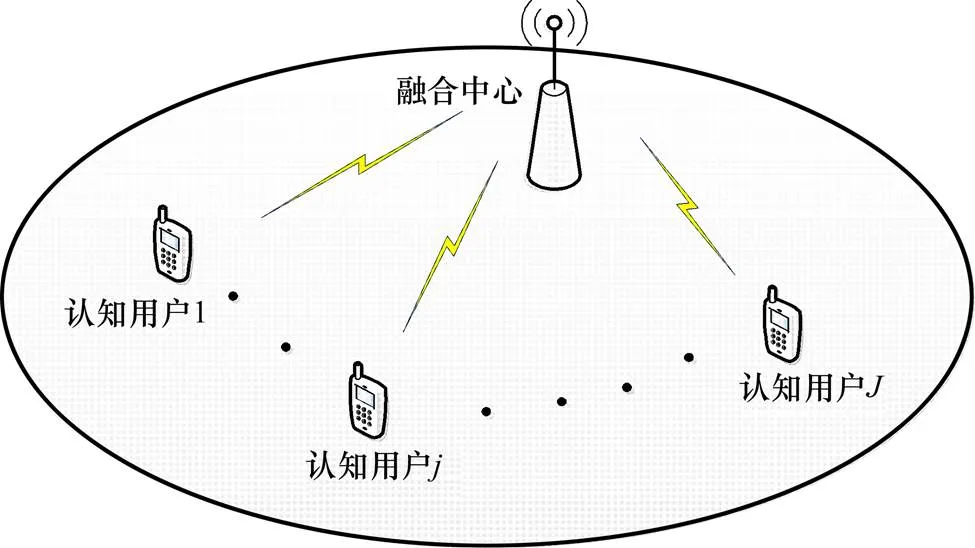
图1 集中式协作频谱感知示意图
1.1 本地压缩频谱感知模型
根据Tian等[3]提出的AIC模型,第个SU的频谱感知框图如图2所示。

图2 AIC模型系统框图
假设总频带是项稀疏的,则第个SU接收到的信号可以表示为:,其中为接收到的第个PU的信号,为信道增益;为加性高斯白噪声,其对应的奈奎斯特采样率下的离散序列为,其对应的频域序列为。则,其中为标准傅里叶正交基。接收信号经过AIC的亚奈奎斯特采样后,得到的离散序列为:。根据文献[3],(其中:对应于伪随机序列(),为对角阵,对角元素等概率地取+1或−1;对应于冲击响应(),为积分下采样矩阵)。
根据压缩感知理论[2],本地信号的重建问题就是求解以下最优化问题:
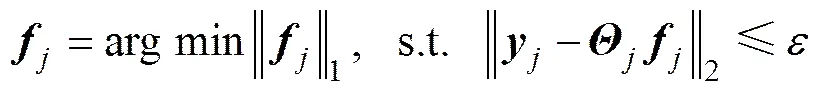
1.2 基于分布式压缩感知的协作频谱感知模型
基于压缩感知的宽带协作频谱感知常用的方法是:在本地感知中进行压缩重构恢复原信号(=1,2,…,),再将发送至融合中心,进行判决。本文提出的方式是SU将亚奈奎斯特速率采样的信息(=1,2,…,),传给FC,再根据分布式压缩感知理论,用适当的算法对整个信道频谱占用情况进行判决。
分布式压缩感知(DCS)理论是Baron于2005年提出的,针对多个信号稀疏性具有相关性的现象,该理论考虑了多个数据源同时稀疏时,利用它们的共同稀疏性可以更准确地重构出原始信号[6−7]。Baron分析了DCS中多个信号之间的互相关性与自相关性,并且已在理论上证明:DCS的重构概率比CS的概率更高。
在本文的模型中,一方面,由于宽带协作频谱感知的整个过程十分短暂,因此,可以假设这段时间内的用户占用频带的状态没有发生改变,及感知过程中整个带宽内的共同的频谱支撑集不变。这符合Duartz等[7]提出的JSM-II模型的特征,不同SU所感知的信号拥有相同稀疏支撑集,即在相同频谱位置有PU信号,但由于无线信号在传播过程中受衰减的影响,PU信号的幅值和相位不同;另一方面,由于信道中存在阴影遮蔽、多径效应的影响,个别SU的频谱支撑集与共同的频谱支撑集存在差异。因此,需要设置不同的权重来排除个别SU的影响,找出共同的频谱支撑集。
根据前面分析和DCS中的JSM-II模型,SU将y送到FC,可以令,,则是项稀疏的,其DCS测量矩阵为

可以看到:具有块对角阵结构,则,=。信号的重建问题就变成求解以下最优化问题:
,;;=1,2,…,
其中:为优化算法的加权系数,。
2 SCoSaMP算法
在现有的基于CS的频谱感知算法中,2种主要的算法是1范数算法和贪婪算法。1范数算法有:基追踪算法BP[8]和它的最优化算法GPSR[9],能够将一个组合优化问题转换成一个凸优化问题。1范数算法能够提供理论上的性能保证。但是,它们对噪声很敏感,而且计算复杂度也很高。而贪婪算法通过迭代近似信号的频谱支撑集来逼近目标信号的频谱支撑集,它对于大尺度的重构问题更有效率。目前,典型的贪婪算法包括正交匹配追踪OMP算法[10]、ROMP算法[11]、SOMP算法[12]。这些算法的复杂性远低于贪婪算法。然而,为了精确重构,它们需要大量的测量数据。当前,更多性能更佳贪婪算法如压缩抽样匹配追踪算法CoSaMP[13]能够提供理论上的性能保证,对噪声有更好的鲁棒性。本文根据DCS理论,基于Needell等[13]中提出的压缩抽样匹配追踪算法CoSaMP,提出一种SCoSaMP算法。
该算法将CoSaMP扩展到DCS场景下,不同之处在于,CoSaMP每次迭代利用测量向量与CS矩阵每列的内积序列,按照贪婪方式选取前2列,加入到信号支撑集的候选集合中;而SCoSaMP充分利用了JSM-2的联合稀疏性,将不同测量向量与对应的CS矩阵求相关,并加权求和后获得新的内积序列,进而选取最匹配的信号序号参与迭代。通过这种联合处理,SCoSaMP的原子选取更为准确。
其中SCoSaMP的加权系数是通过以下优化问题来确定的:
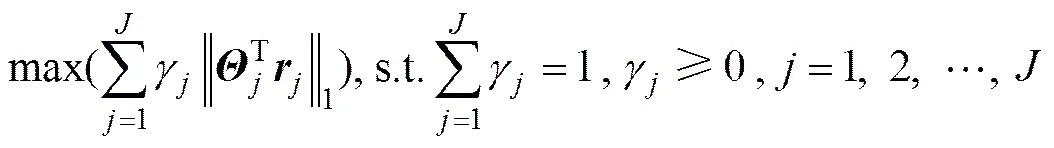
根据Schwartz不等式
使上式等号成立的充分条件为

因此,可令
文献[13]已经证明,给定任意精度参数,CoSaMP算法重构出的近似信号满足不等式:
为稀疏度为时的最佳表示;为信号噪声,这就保证了算法的性能,而SCoSaMP算法由于应用了DCS的思想,对信号的频谱支撑集做了进一步的优化,因此比CoSaMP算法具有更佳的性能保证。
SCoSaMP算法的伪代码如表1所示。

表1 SCoSaMP算法的伪代码
3 仿真与分析
利用Matlab2009进行仿真实验,在加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道下,对SCoSaMP算法的重构性能,协作感知降低滤波器数目的效率以及用户数量对算法性能的影响进行了仿真分析。仿真共设置了200个子信道,每个子信道的带宽为2 MHz。
不同信噪比下,OMP,DCS-SOMP和SCoSaMP算法的归一化的最小均方误差MS如图3所示。仿真环境设定:协作感知的SU个数=3(OMP算法的=1),信道的稀疏度=20,每个SU的滤波器数目=60。从图3可以看出:协作频谱感知的性能优于本地压缩频谱感知(DCS-SOMP和SCoSaMP算法优于OMP算法),SCoSaMP算法性能优于Duarte等[7]提出的DCS-SOMP算法。
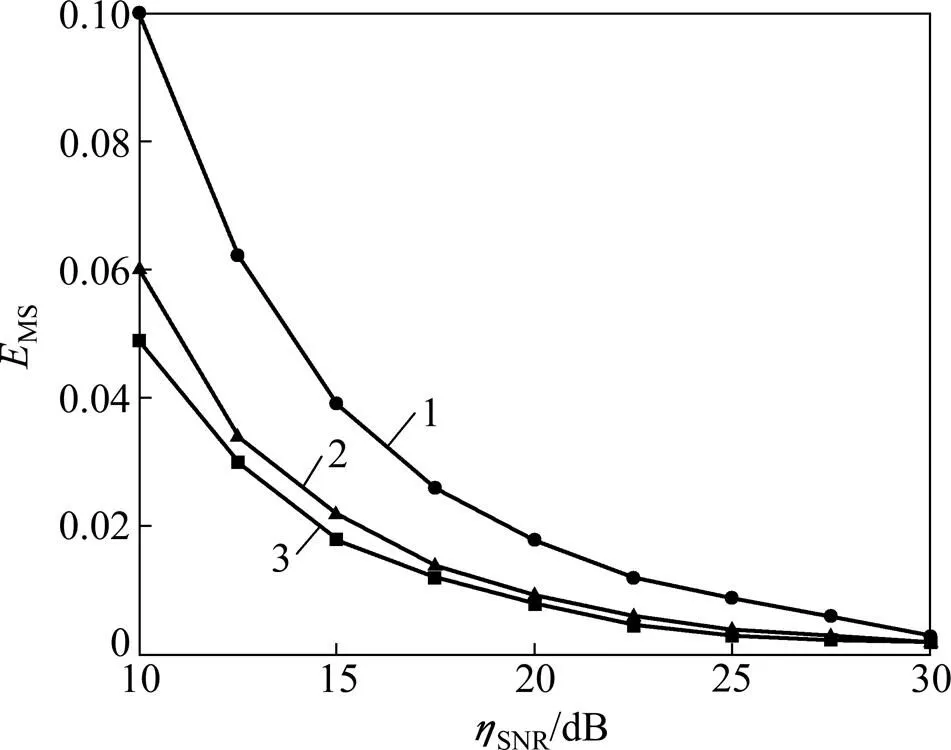
1—OMP算法;2—DCS-SOMP算法;3—SCoSaMP算法
图4显示了SCoSaMP算法与DCS-SOMP算法成功重构信号的前提下,信噪比SNR与SU所需最小滤波器数目间的关系,仿真环境为瑞利衰落信道。由图4可以看出:当SNR=10 dB,=3时,DCS-SOMP算法所需的滤波器数约为57,而SCoSaMP算法所需的滤波器数约为53;当SNR=10 dB,=5时,DCS-SOMP算法所需的滤波器数约为38,而SCoSaMP算法所需的滤波器数约为36。因此,可以得出:在相同信噪比环境和SU数目的情况下,SCoSaMP算法所需的滤波器数少于DCS-SOMP算法。
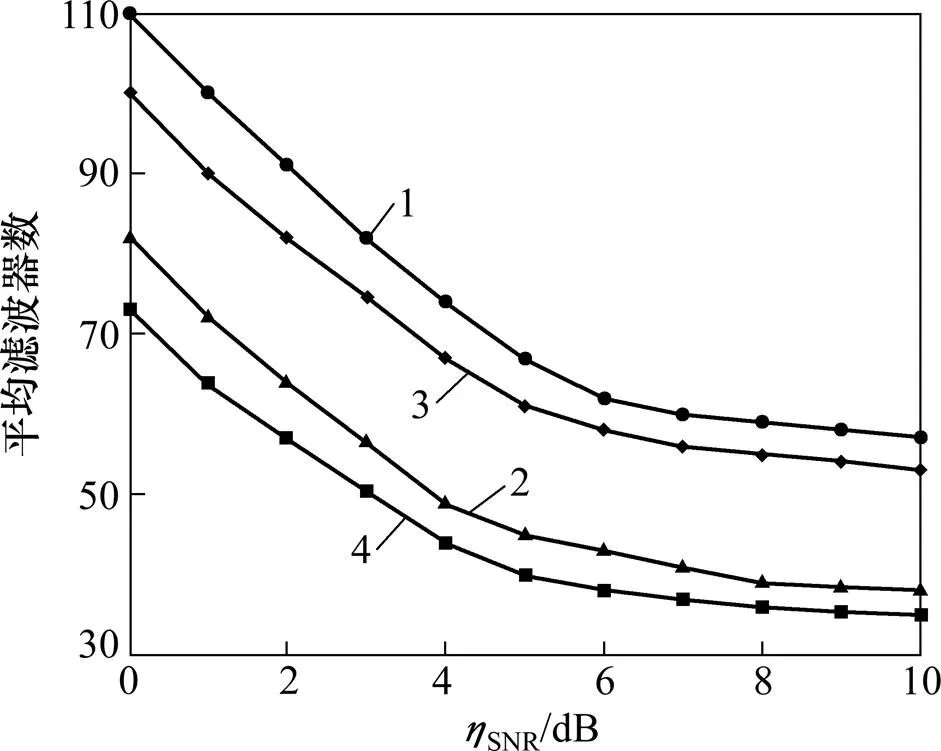
1—DCS-SOMP算法,J=3;2—DCS-SOMP算法,J=5;3—SCoSaMP算法,J=3;4—SCoSaMP算法,J=5
图5通过比较不同用户数量情况下,SCoSaMP算法的ROC性能,分析了该算法与用户数量之间的关系。仿真环境设定:协作感知的SU个数=3,5,7,信道的稀疏度=20,每个SU的滤波器数=60。从图5可以看出:在相同虚警概率下,检测概率随用户数量的增加而增大;同时,随用户数量的增加,检测概率的增大幅度逐渐变小。
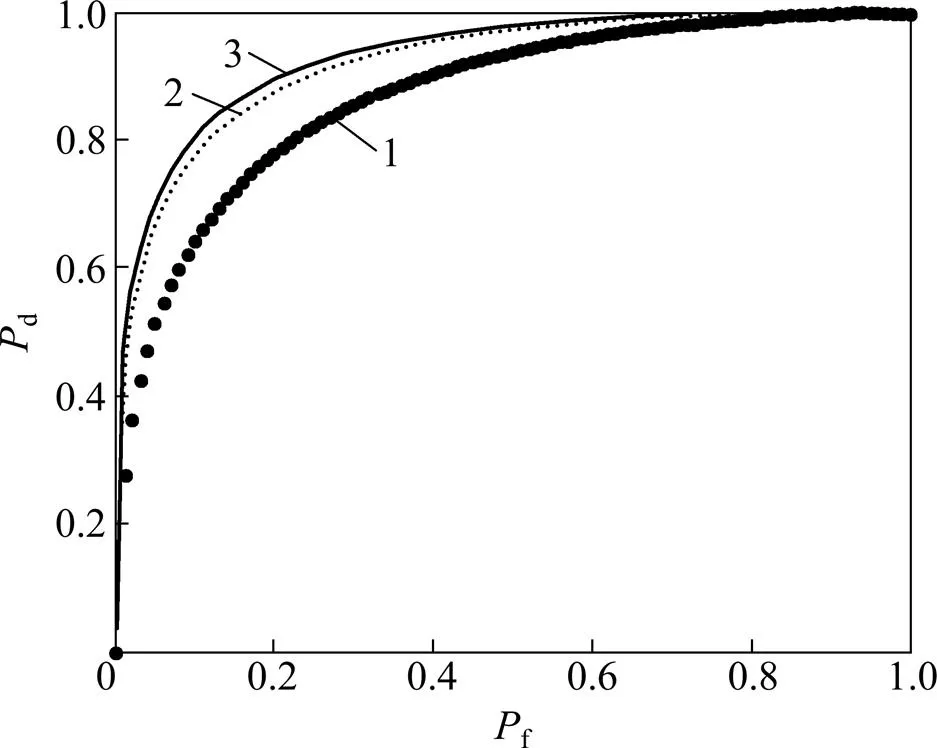
J:1—3;2—5;3—7
4 结束语
1) 考虑到压缩频谱感知融合中心的数据传输压力,提出一种基于分布式压缩感知理论的宽带协作频谱感知的方法。同时考虑到对噪声有更好的鲁棒性与理论上的性能保证,提出一种联合压缩抽样匹配追踪算法—SCoSaMP算法。
2) 仿真结果证明,本文作者提出的算法具有更好的检测性能,对于认知无线电宽带协作频谱感知有一定的实际应用价值。
[1] Haykin S. Spectrum sensing for cognitive radio[J]. Proceedings of the IEEE, 2009, 97(5): 849−877.
[2] Candes E, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489−509.
[3] Tian Z, Giannakis G B. Compressed sensing for wideband cognitive radios[C]// Ieee International Conference On Acoustics Speech and Signal Processing. Honolulu, USA: IEEE, 2007: 1357−1360.
[4] 曾凡仔, 刘洁, 李仁发, 等. 基于一致优化的分布式宽带合作频谱感知算法[J]. 通信学报, 2011, 32(9): 147−152. ZENG Fanzi, LIU Jie, LI Renfa, et al. Distributed cooperative spectrum sensing based on consensus optimization[J]. Journal on Communications, 2011, 32(9): 147−152.
[5] 顾彬, 杨震, 胡海峰. 基于压缩感知信道能量观测的协作频谱感知算法[J]. 电子与信息学报, 2012, 34(1): 14−19. GU Bin, YANG Zhen, HU Haifeng. Cooperative wideband spectrum sensing algorithm based on compressed sensing channel energy measurements[J]. Journal of Electronics & Information Technology, 2012, 34(1): 14−19.
[6] Baron D, Duarte M F, Sarvotham S, et al. An information-theoretic approach to distributed compressed sensing[EB/OL]. [2012−08−07]. https://dsp.rice.edu/sites/ dsp.rice.edu/files/publications/conference-paper/2005/aninfor-acccc-2005.pdf.
[7] Duarte M, Wakin M, Baron D, et al. Universal distributed sensing via random projections[C]//The Fifth International Conference on Information Processing in Sensor Networks. Nashville, Tennessee, USA: IPSN , 2006: 177−185.
[8] Donoho D L. Compressed sensing[J]. IEEE Trans Inf Theory, 2006, 52(4): 1289−1306.
[9] Figueiredo M, Nowak R, Wright S. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. IEEE J Sel Topics Signal Process, 2007, 1(4): 586−597.
[10] Tropp J, Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Trans Inf Theory, 2007, 53(12): 4655−4666.
[11] Needell D, Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2009, 9(3): 317−334.
[12] Tropp J, Gilbert A C, Strauss M J. Simultaneous sparse approximation via greedy pursuit[C]//IEEE Int Conf Acoustics, Speech, Signal Proc (ICASSP). Philadelphia, USA, 2005: 721−724.
[13] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301−321.
(编辑 陈爱华)
Wideband cooperative spectrum sensing based on distributed compressed sensing
SU Yidong, DA Xinyu
(Information and Navigation Institute, Air Force Engineering University, Xi’an 710077, China)
Based on the theory of distributed compressed sensing, a wideband cooperative spectrum sensing approach was proposed. Compared to the previous ways of cooperative compressed spectrum sensing, the data of cognitive users transfer to fusion center was simplified to compressed signal, and each compressed signal at the fusion center was fused and reconstructed, thus it reduced the amount of data transfer to the fusion center, eased the pressure data fusion center, and could improve the success rate of signal reconstruction. At the same time, according to the compression sampling matching pursuit algorithm, a simultaneous compression sampling matching pursuit algorithm was put forward. By weighting fusion measuring samples, iteration reconstructing the original signal, restoring joint spectrum support set, the algorithm completed the cooperative spectrum sensing. The simulation results show that compared with classic DCS-SOMP algorithm, this algorithm has better performance, less number of filter.
distributed compressed sensing; cooperative spectrum sensing; cognitive radio
10.11817/j.issn.1672-7207.2015.06.018
TN914
A
1672−7207(2015)06−2104−05
2014−06−13;
2014−08−20
国家自然科学基金资助项目(61271250)(Project (61271250) supported by the National Natural Science Foundation of China)
苏一栋,博士研究生,从事认知无线电、压缩感知、频谱感知研究;E-mail:drsuyidong@gmail.com

