软土地区土压平衡盾构反扭矩分析

梁荣柱，夏唐代，林存刚，孟万斌，吴昊



软土地区土压平衡盾构反扭矩分析

梁荣柱1, 2，夏唐代1, 2，林存刚3，孟万斌4，吴昊5

(1. 浙江大学建筑工程学院，浙江杭州，310058；2. 浙江大学滨海和城市岩土工程研究中心，浙江杭州，310058；3. 宁波大学建筑工程与环境学院，浙江宁波，315211；4. 杭州市地铁集团有限责任公司，浙江杭州，310000；5. 中南大学地球科学与信息物理学院，湖南长沙，410083)

基于土力学基本原理，综合考虑覆土、盾构自重及未脱开管片自重、千斤顶反力因素等产生的阻滞力矩，推导出在软土地层中盾构施工反扭矩理论计算方法。通过杭州软土地区盾构地铁区间实例分析，发现理论计算反扭矩为实测切削扭矩18.9到16.0倍，表明在盾构切削施工过程中，反扭矩足够保证盾构正常掘进而不会有产生侧翻的可能。在盾构始发掘进时，虽然理论计算反扭矩大于实测切削扭矩，但是安全系数较小。提出一种简单有效防止侧翻的措施并应用于实践。由于软黏土的黏滞特性，在刀盘切削扭矩作用下盾构体轻微回转，通过反向调整切削方向可以消除盾构回转角。

土压平衡盾构机；阻滞力矩；软土；隧道施工

盾构隧道法施工有占地面积少、安全、高效、不影响地面交通、机械化程度高等优点，现已被广泛应用于城市地铁隧道建设[1−2]。在盾构掘进参数中，切削扭矩是保证盾构切削顺利进行的重要参数。众多学者对盾构机扭矩理论计算进行深入的研究，并成功应用于盾构设计之中[3−13]。值得注意的是，在盾构机切削岩土体时，必须有大于切削扭矩的反作用，才能确保盾构顺利掘进而不产生侧翻，这个作用就是“反扭矩”。当反扭矩大于切削扭矩，可以保证盾构切削顺利进行；但当切削扭矩大于反扭矩，则盾构机有侧翻的危险。在掘进中发生盾构机侧翻纠正难度大，严重影响施工进度，造成巨大经济损失。鲜有文献对反扭矩进行较深入分析讨论。郭玉海等[14]基于土力学基本原理，认为在盾构掘进过程中，盾构机受到覆土产生的阻滞力矩和自重产生的阻滞力矩，两者之和为施工反扭矩，建立盾构在掘进及始发2种模式下反扭矩数学模型。然而文献[14]忽略了侧向土压力对阻滞力矩的贡献，同时没有考虑到在掘进过程中始终受力的千斤顶垫板与管片之间摩擦力及在盾构体内若干管片重力对阻滞力矩的贡献。在文献[14]的基础上，本文作者基于土力学基本原理，考虑侧向土压力、千斤顶反力对盾构反扭矩的贡献，进一步完善在软土地区盾构掘进反扭矩理论计算，通过正常掘进及盾构始发掘进2种情况反扭矩计算与某地铁区间盾构隧道实际盾构切削扭矩对比，并给出始发施工中简单有效的预防侧翻的措施，最后基于盾构姿态实测数据讨论盾构掘进回转角产生原因及减少回转角的措施。本文作者的研究成果可以为软土盾构施工反扭矩分析及施工提供理论计算依据。

1 软土地层掘进中盾构反扭矩分析

在软土地层掘进中，盾构动力系统提供扭矩，刀盘得以切削土体。这就要求有足够大的反扭矩，才能确保盾构机在掘进过程中不产生翻滚。在掘进期间，盾构机反扭矩主要由如下3个方面构成：覆土产生的阻滞力矩、盾构机及未脱出管片重力产生的阻滞力矩、千斤顶反力作用于管片产生的摩擦阻滞力矩。掘进期间，盾构机所受荷载作用如图1所示。

图1 盾构荷载示意图

1.1 覆土产生的阻滞力矩

在盾构机产生转动或有转动的趋势时，地层及机体将产生阻碍盾构机转动的动、静摩擦力力矩。在盾构掘进中不允许盾构机发生明显的转动，因此作用于盾构机的阻滞力矩为静止摩擦力矩。

盾构体受力分解如图2所示。盾构体上任意角度竖向正压力为

则盾构体上任意角度侧向正压力为

式中：0为侧向静止土压力系数；为盾构轴线位置竖向压力，kPa；为湿重度，kN/m3；为盾构机外径，m。

由弹性力学求任意角度法向总应力公式，可得到盾构体径向任意角度总应力：

取盾壳上弧长d，其对应圆心角为，d=d，覆土产生的阻滞力矩1为

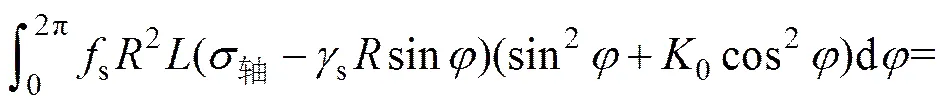
式中：s为盾构与周围土体静摩擦力因数；为盾构机长度，m。

1.2 机体自重及管片重力产生的阻滞力矩

盾构机质量大，在重力作用下将产生阻滞力矩。未脱开盾构管片，在盾构扭转切削过程中提供阻滞力矩亦不可忽视。

盾构机重力及未脱开管片重力产生的盾构机下部地层反力g为

式中：s为盾构机重力，kN；seg为每环管片重力，kN；为未脱出机体的管片环数。

地层反力g作于盾构下部产生的垂直于盾构体的法向应力p为

地层反力g产生的阻滞力矩2为

1.3 千斤顶反力产生的阻滞力矩

掘进过程中，盾构千斤顶推力作用于管片上，盾构机在反力作用下得以推进。在盾构机转动或有转动趋势的情况下，在千斤顶正压力作用于管片产生动摩擦力或静摩擦力，受力分析如图3所示。各个千斤顶动、静摩擦力产生阻滞力矩3计算公式如下：

式中：r为千斤顶撑靴与混凝土管片的静摩擦因数；Ni为第个千斤顶作用于管片上的力，kN；IS为千斤顶轴线到盾构机轴线的距离，m；N为每环总推 力，kN。

1.4 掘进过程中反扭矩

掘进过程中反扭矩等于覆土产生的阻滞力矩1，盾构自重及管片重力产生的阻滞力矩2加上千斤顶垫片与管片产生的阻滞力矩3之和，即为

2 工程实例分析

杭州地铁二号线某区间位于萧山区内，隧道平面如图4(a)所示。本文就上行线NP15~300环及下行线PN 835~1130环，即始发基坑18~372 m范围内反扭矩进行分析。隧道的掘进施工采用的是日本小松(KOMASTU)机械公司生产的土压平衡盾构机。盾构机外径=6.34 m，盾构机重4 500 kN，机体长为8.68 m。隧道管片为预制钢筋混凝土管片，强度等级C50。管片外径o=6.2 m，内径i=5.5 m，每环宽1.2 m。管片采用6环(3块标准块，2块相邻块和1块小封顶块管片)错缝拼装，管片纵向及环向均采用高强度弯螺栓连接。

掘进平面图如图4(a)所示，地表较为开阔，地势平坦。施工掘进穿越的地层为杭州典型软土地层，NP1~NP310环(PN835~1130)地质剖面图如图4(b)所示。在掘进范围内，穿越土层主要为淤泥质粉质黏土④1，淤泥质黏土④2。淤泥质粉质黏土④1及淤泥质黏土④2基本力学参数见表1。从图4发现：④1标贯击数在1~3击，④2标贯击数在2~3击范围，天然承载力分别只有60~65 kPa，可见掘进地层属于典型的软黏土，地基承载力较低。各土层物理力学指标参数见表1。

(a) 掘进平面图；(b) 地质剖面图

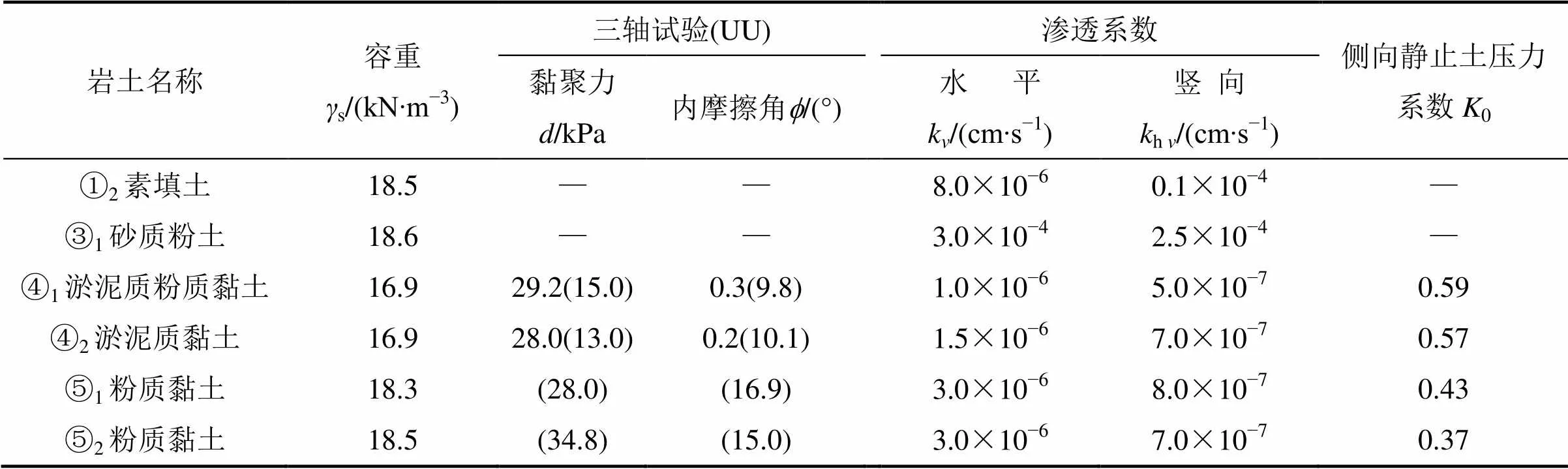
表1 场地主要土层物理力学指标

注：括号内为固结快剪试验结果。

计算参数如下。场地地面多为农田，故认为地面超载0=0；由勘察报告建议：④1层静止侧向土压力系数0取0.59；本工程盾构机重4 500 kN；混凝土重度取C=25 kN/m3，每环混凝土管片重力为seg=192.9 kN；在盾构机壳与软土层静摩擦因数s取值上，于颖等[14]认为此值应取0.23，苏建行等[15]建议在黏性土中取值在0.2~0.3范围，施虎等[16]在黏土盾构机取值为0.3；吕强等[10]认为在黏土中取值0.2，为简化计算取静摩擦因数s=0.2。根据经验取混凝土管片与硬脂橡胶垫板摩擦因数r=0.1；千斤顶轴线到盾构机轴线的距离IS为2.87 m。每环千斤顶总推力由盾构机控制系统记录获得。

2.1 正常掘进反扭矩分析

计算所得结果如图5所示。距离N始发基坑18~372 m范围内，上、下行线掘进平均扭矩分别为 1 193.2 kN·m及1 405.5 kN·m，而计算得到相对应的平均阻滞力矩：上行线为22 558 kN·m，下行线为 22 509 kN·m，分别为实测切削力矩的18.9倍及16.0倍之多。可见在软土地层中盾构掘进时，地层及机器本身提供的阻滞力矩足以抵消实际切削力矩，理论上在掘进过程中盾构机不会出现侧翻现象。

1—上行线计算反扭矩；2—下行线计算反扭矩；3—上行线实测刀盘扭矩；4—下行线实测刀盘扭矩

各个因素产生的阻滞力矩与总阻滞力矩之比见图6和7。由图6和7可见，上及下行线各阻滞力矩与总扭矩之比相差较大。在所有的产生阻滞力矩因素中，覆土提供的阻滞力矩是所有因素中占的比例最大，分别为上下行线总反扭矩的80%及79%；重力产生的阻滞力矩对总阻滞力矩贡献为11%；千斤顶反力产生的阻滞力矩对总扭矩贡献分别为9%和10%。千斤顶反力产生的阻滞力矩对总阻滞力矩是不可忽略的。文献[14]并未考虑千斤顶反力产生的阻滞力矩，导致计算反扭矩小于实际可提供的反扭矩。隧道轴线位置竖向土压力分布见图8。对比图5和8：竖向土压力分布与计算反扭矩分布基本一致，说明在正常掘进条件下，隧道埋深越大，可提供的反扭矩中重力提供的阻滞力矩也越大。

1—M1；2—M2；3—M3

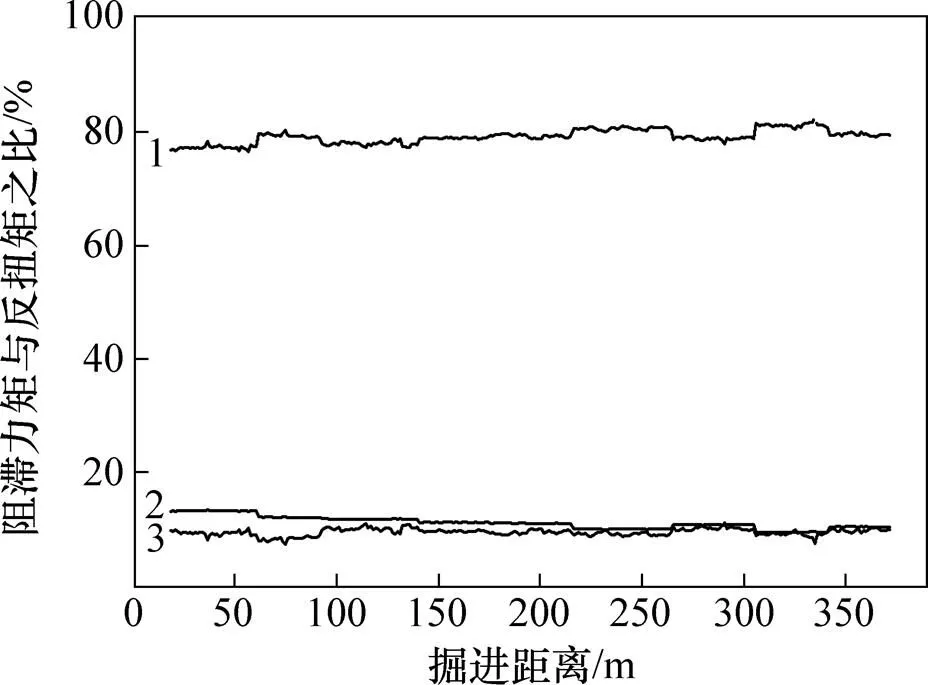
1—M1；2—M2；3—M3

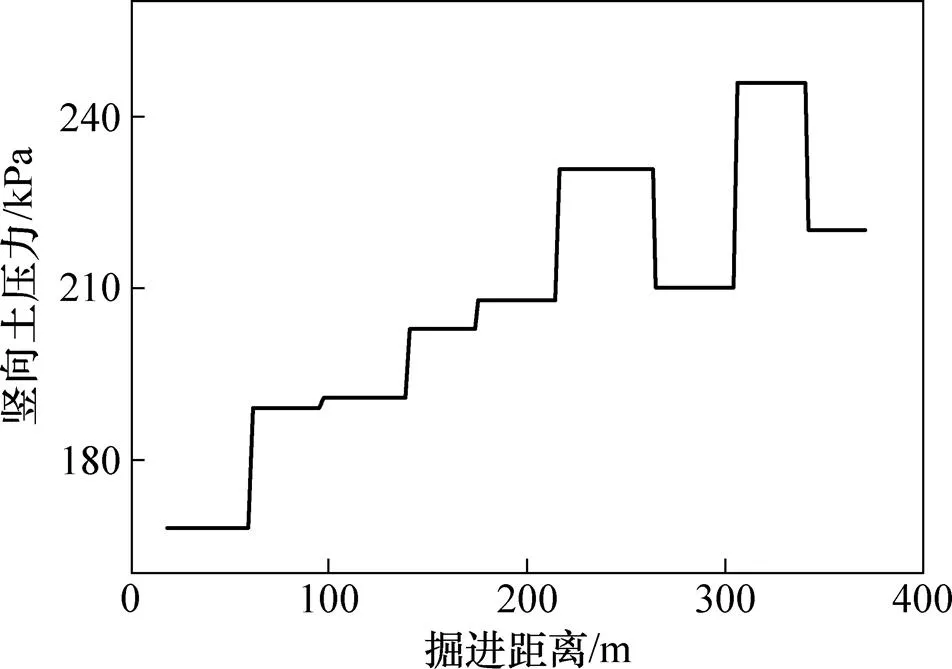
图8 隧道轴线处竖向土压力分布

2.2 始发过程反扭矩分析

盾构始发是盾构施工最容易出现施工事故的工况之一。盾构机始发如图9所示，在盾构始发时，盾构机安装在钢托架上。

(a) 正视图；(b) 侧视图

盾构机进入加固地层时，机体上方并无覆土，因此覆土提供的阻滞力矩1为0 kN∙m。

始发过程中，盾构机一部分在加固地层中，另一部分在钢托架上，因此重力提供的阻滞力矩分2个部分：一部分盾构机与刚托架静摩擦力提供的阻滞力矩21′；另一部分为在加固地层中盾构机提供的阻滞力矩22′。值得注意是，盾构机进入加固土层后，由于在加固地层中掘进，往往采用仿形刀切削，切削半径大于盾构外径，加固地层有良好自稳能力，竖向土压力不传递到盾构机体上，因此不计算覆土产生的阻滞力矩，并假定盾构机重力沿机身均匀分布。分别计算如下：

式中：1为盾构机体与托架静摩擦力系数，取0.10；为掘进长度；s′为盾构机体与加固地层静摩擦因数，取0.2。

则在始发阶段重力提供阻滞力矩为

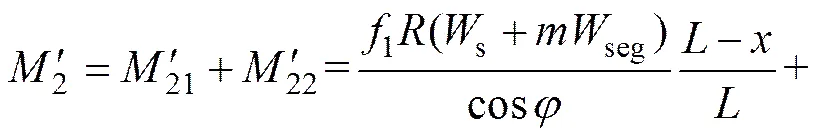
千斤顶反力提供的阻力力矩与正常掘进计算一样，3′=3，见式(8)。

在加固地层掘进过程中，总反扭矩为

在掘进区间两端盾构始发，穿越12 m长加固区。分别计算掘进加固区两加固区反扭矩，得到反扭矩与切削扭矩关系如图10所示。

1—上行线切削扭矩；2—上行线反扭矩；3—下行线切削扭矩；4—下行线反扭矩

图10 盾构始发切削扭矩与反扭矩关系

Fig. 10 Relationship between cutting torques and reverse torques during shield originating in improved ground

从图10可见：盾构反扭矩略大于切削扭矩，理论上仍可以维持盾构顺利掘进，且最初三环掘进是盾构机最不利施工工况，安全系数较低，在1.5~1.8之间。图11所示为各个因素占反扭矩之比。由图11发现在前三环掘进中，重力提供的阻滞力矩略大于千斤顶反力贡献百分比，随着掘进深入千斤顶反力贡献率大于重力提供的阻滞力矩。虽然在理论上证明在盾构始发最不利条件下，计算反扭矩大于切削扭矩，而千斤顶反力阻力力矩决定于盾构推力，导致反扭矩有较大的不确定性。为预防盾构翻滚，提出一种简单有效的预防措施：在盾构机体上焊接钢块(见图9)，防止盾构机回转。随着盾构进入土层而切除相应位置的钢块。该方法成功应用于本工程盾构始发施工。

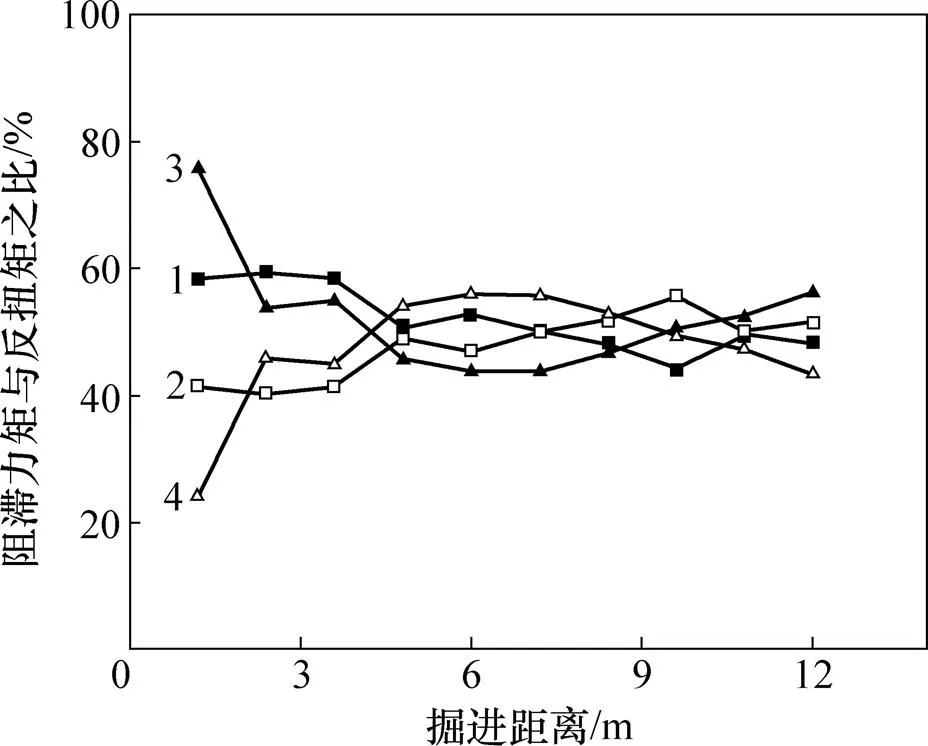
1—M2′(上行线)；2—M3′(上行线)；3—M2′(下行线)；4—M3′(下行线)

3 盾构回转角分析

由以上计算分析可知：从理论上表明在切削过程盾构机不会产生侧翻的可能，而在实际盾构机切削施工中，从实测数据显示盾构机机体依然会产生轻微转动。图12(a)和(b)所示分别为盾构机在NP 1~310(PN 835~1145)实测回转角。

(a) NP1-310；(b) PN835-1145

图13(a)和(b)给出部分环号掘进时刀盘扭矩与回转角的关系变化。图中以盾构顺时针回转方向为正。由图13可见：在盾构刀盘向一个方向回转切削时，盾构体回转方向与刀盘运动方向一致。这是由于软黏土具有黏滞特性，在切削扭矩的作用下，握裹盾体软黏土类似遭受土工试验中“单剪试验”，导致尽管远小于阻滞力矩但周围土体仍然产生剪切变形，最终导致盾构体轻微回转。

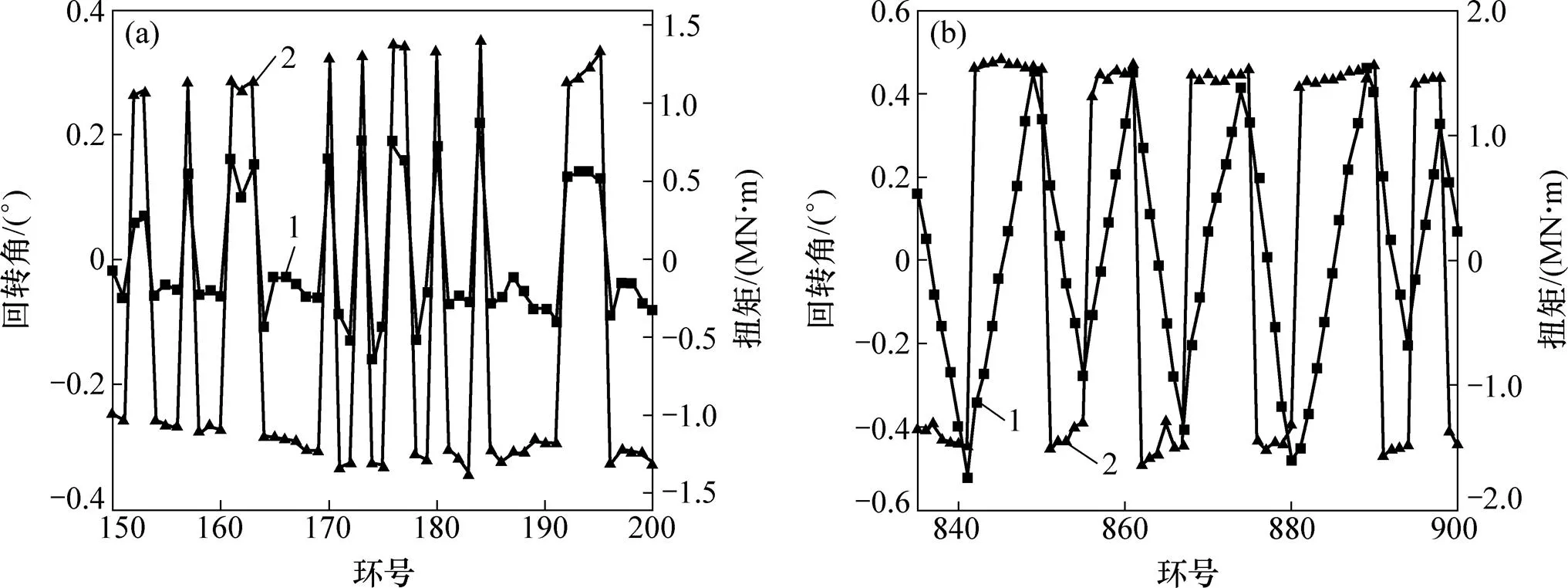
(a) NP150-200；(b) PN835-890

在实际操作过程中，盾构体轻微回转现象应该引起足够重视，过大的回转角将会影响管片拼装的质量。减少回转角最简单有效的方法为：避免长时间朝一个方向回转切削；当回转角超过设定值时，及时反向回转刀盘。

4 结论

1) 基于土力学基本原理，进一步完善了掘进施工中盾构反扭矩理论计算。通过实例验证，在正常掘进过程中，总反扭矩提供足够的阻滞力矩，是实际切削扭矩的18.9到16.0倍，确保掘进过程中盾构体不发生侧翻。在众多影响盾构反扭矩的因素中，千斤顶反力对总反扭矩贡献不可忽略。

2) 盾构始发提供的反扭矩虽然大于切削扭矩，但是安全系数较小。通过焊接小钢块在盾体上可以有效预防盾体侧翻。

3) 由于软黏土黏滞特性，在盾构扭矩作用下盾体产生较小回转角。通过反方向回转刀盘可以消除回转角。

[1] 周文波. 盾构法隧道施工技术及应用[M]. 北京: 中国建筑工业出版社, 2004: 18−21. ZHOU Wenbo. Shield tunneling technology[M]. Beijing: China Architecture & Building Press, 2004: 18−21.

[2] 张凤祥, 朱合华, 傅德明. 盾构隧道[M]. 北京: 人民交通出版社, 2004: 1−7. ZHENG Fengxiang, ZHU Hehua, FU Deming. Shield tunneling method[M]. Beijing: China Communications Press, 2004: 1−7.

[3] 管会生, 高波. 盾构刀盘扭矩估算理论模型[J]. 西南交通大学学报, 2008, 43(2): 213−217, 226. GUAN Huisheng, GAO Bo. Theoretical model for estimation of cutter head torque in shield tunneling[J]. Journal of Southwest Jiaotong University, 2008, 43(2): 213−217, 226.

[4] 管会生, 高波. 复合式土压平衡盾构道具切削扭矩的研究[J]. 现代隧道技术, 2008, 45(2): 73−78. GUAN Huisheng, GAO Bo.Study on the cutting torque of cutters of composite EPB shield[J]. Modern Tunneling Technology, 2008, 45(2): 73−78.

[5] 王洪新. 土压平衡盾构刀盘扭矩计算及其与盾构施工参数关系研究[J]. 土木工程学报, 2009, 42(9): 109−113. WANG Hongxin. Calculation of cutterhead torque for EPB shield and the relationship between cutterhead torque and shield driving parameters[J]. China Civil Engineering Journal, 2009, 42(9): 109−113.

[6] HU Shi, YANG Huayong, GONG Guofang, et al.Determina- tion of the cutterhead torque for EPB shield tunneling machine[J]. Automation in Construction, 2011, 20(8): 1087−1095.

[7] Uger A, Nuh B, Hanifi C. Estimating torque, thrust and other design parameters of different type TBMs with some criticism to TBMs used in Turkish tunneling projects[J]. Tunneling and Underground Space Technology, 2014, 40(2): 46−63.

[8] 刑彤, 龚国芳, 杨华勇. 盾构刀盘驱动扭矩计算模型及实验研究[J]. 浙江大学学报(工学版), 2009, 43(10): 1794−1800. XING Tong, GONG Guofang, YANG Huayong. Torque calculation model of cutting head in shield machine and experimental study[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(10): 1794−1800.

[9] 徐前卫, 朱合华, 丁文其, 等. 均质地层中土压平衡盾构施工刀盘切削扭矩分析[J]. 岩土工程学报, 2010, 32(1): 47−54. XU Qianwei, ZHU Hehua, DING Wenqi, et al. Cutting torque during tunneling process of earth pressure balance shield machine in homogeneous ground[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1): 47−54.

[10] 吕强, 傅德明. 土压平衡盾构掘进机刀盘扭矩模拟试验研究[J]. 岩石力学与工程学报, 2006, 25(增1), 3137−3143.LÜ Qiang, FU Deming. Research on torque of cutterhead for earth pressure balance shield with simulating experimental[J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S1): 3137−3143.

[11] 陈仁朋, 刘源, 汤旅军, 等. 复杂地层土压平衡盾构机推力和刀盘扭矩计算[J]. 地下空间与工程学报, 2012, 8(1): 26−32. CHEN Renpeng, LIU Yuan, TANG Lüjun et al. Research on calculation of thrust and cutter head torque on shield in complex strata[J]. Chinese Journal of Underground space and Engineering, 2012, 8(1): 26−32.

[12] 李潮, 周宏伟, 左建平, 等. 土压平衡盾构刀盘扭矩计算方法与多因素量化分析[J]. 岩石力学与工程学报, 2013, 32(4): 760−766. LI Chao, ZHOU Hongwei, ZUO Jianping, et al. Torque calculation method of cutterhead in earth pressure balance shield and quantitative analysis of several influencing factors[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 760−766.

[13] 于颖, 徐宝富, 奚鹰, 等. 软土地基土压平衡盾构切削刀盘扭矩的计算[J]. 中国工程机械学报, 2004, 2(3): 314−318. YU Ying, XU Baofu, XI Ying, et al. Torque moment analysis of earth pressure balanced shield cutter head under soft foundation[J]. Chinese Journal of Construction Machinery, 2004, 2(3): 314−318.

[14] 郭玉海, 王梦恕, 张照煌, 等. 土压平衡盾构反扭矩的分析和计算[J]. 岩土力学, 2013, 34(5): 1449−1452. GUO Yuhai, WANG Mengshu, ZHANG Zhaohuang, et al. Analysis and calculation of reverse torque of earth pressure balance shield[J]. Rock and Soil Mechanics, 2013, 34(5): 1449−1452.

[15] 苏健行, 龚国芳, 杨华勇. 土压平衡盾构掘进总推力的计算与试验研究[J]. 工程机械, 2008, 39(1): 13−16. SU Jianxing, GONG Guofang, YANG Huayong. Calculation and experimental research of driving trust of EPB shield[J]. Engineering Machine, 2008, 39(1): 13−16.

[16] 施虎, 龚国芳, 杨华勇, 等. 盾构掘进机推进力计算模型[J].浙江大学学报(工学版), 2011, 45(1): 126−131. SHI Hu, GONG Guofang, YANG Huayong et al. Determination of thrust force for shield for shield tunneling machine[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(1): 126−131.

Analysis of reverse torque of EPB shield tunneling in soft ground

LIANG Rongzhu1, 2, XIA Tangdai1, 2, LIN Cungang3, MENG Wanbin4, WU Hao5

(1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China;2. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;3. College of Civil, Construction and Environmental Engineering, Ningbo University, Ningbo 315211, China;4. Hangzhou Metro Corporation Ltd., Hangzhou 310000, China;5. School of Geosciences and Info-physics, Central South University, Changsha 410083, China)

Based on the principles of soil mechanics, a theoretical calculation method for computing the reverse torque of Earth Pressure Balanced shield driving in soft ground was derived by considering lots of relative factors, including the resistant moments induced by soft soil around shield body, the gravity of shield and segments left in shield, and the reaction force of jack thrust. The theoretical calculation method was verified through a case history of a metro tunnel section in Hangzhou soft ground. The reverse torques calculated by the proposed method are approximately 18.9 to 16 times of the measured cutting torques, which implies that the inherent reverse torque of shield can effectively prevent the shield from rolling during the advancing process. In the start stage, although the theoretical calculated reverse torques were still larger than the measured torques, they have low safe factors. A simple but effective method was proposed to prevent shield from rolling in the start stage in the improved ground. Its effectiveness was verified successfully in actual engineering practice. Due to the viscous of soft soils, slight rolling angles of shield body were observed when the cutter head was rotating in one single direction during the advancing process. The rolling angles can be effectively eliminated by adjusting the cutter head in the opposite direction.

EPB shield machine; resistance moment; soft ground; tunneling excavation

10.11817/j.issn.1672-7207.2015.10.035

U455.43

A

1672−7207(2015)10−3814−08

2015−02−26；

2015−05−30

国家自然科学基金高速铁路基础研究联合基金重点资助项目(U1234204)(Project (U1234204) supported by the National Natural Science Foundation of China)

夏唐代，博士，教授，博士生导师，从事土动力学及地下工程研究；E-mail：xtd@zju.edu.cn

(编辑 陈爱华)