考虑分形裂纹弯折效应和长度效应的水力压裂裂缝扩展机理
李小刚,易良平,杨兆中,周拿云(.西南石油大学油气藏地质及开发工程国家重点实验室,成都60500;.中国石油西南油气田分公司采气工程研究院,四川广汉68300)
考虑分形裂纹弯折效应和长度效应的水力压裂裂缝扩展机理
李小刚1,易良平1,杨兆中1,周拿云2
(1.西南石油大学油气藏地质及开发工程国家重点实验室,成都610500;2.中国石油西南油气田分公司采气工程研究院,四川广汉618300)
为了更加准确地认识裂缝分形扩展对水力压裂的影响,针对传统的线性扩展模型,考虑分形裂纹弯折效应和长度效应,重新推导了裂缝在分形扩展下的断裂韧性表达式,从而导出新的水力裂缝缝宽方程以及水力裂缝扩展所需的缝内净压力表达式。理论分析表明,裂缝扩展弯折角越大,分形维数越大;与水力裂缝线性扩展模型相比,考虑裂缝的分形裂纹弯折效应和长度效应后,水力裂缝扩展所需的缝内净压力更大。与裂缝线性扩展模型相比,裂缝分形扩展模型计算得到的缝宽在裂缝的前80%部分是减小的,只有在靠近裂缝端部缝宽是增加的,即用线性扩展模型算出的缝宽较实际情况偏大,所以线性扩展模型中能够安全通过的支撑剂在实际情形中可能形成桥堵。
水力压裂;分形扩展;弯折效应;缝宽方程;断裂韧性
传统的水力裂缝延伸模型是建立在裂缝线性扩展基础上的,实际上,无论是在宏观层面还是微观层面,大部分岩石断面都是粗糙不规则的[1-4],对于页岩、砂砾岩储集层,这种情况尤甚[5-9],所以水力裂缝的非线性几何形态难以用欧式几何进行描述,Mandelbort创立的分形几何理论为解决此问题提供了有效途径。与线性扩展相比,裂缝的分形扩展改变了应力场的分布特征及宏观线性长度上的岩石断裂韧性[10-12],从而使得水力裂缝形态和裂缝扩展所需的缝内净压力发生变化。近20年来,有学者研究了分形裂缝长度效应对水力裂缝起裂、延伸以及裂缝形态的影响,却没有考虑分形裂纹的弯折效应对水力压裂的影响[10,13-16]。本文考虑分形裂纹的弯折效应(引起应力场的改变)和分形裂纹不规则扩展的长度效应(引起更多的能量耗散)来重新表征岩石的应力强度因子[17],旨在更新水力压裂裂缝的几何尺寸模型。
1 断裂理论基础
由断裂理论可知,裂纹开始扩展的判据有2种:一种是基于应力强度因子的判据,称为K判据,即认为应力强度因子K达到材料断裂韧性KC时裂纹开始扩展;另一种是基于能量释放率的判据,称为G判据,即认为能量释放率G达到临界能量释放率GC时裂纹开始扩展。因为在平面应变条件下[18]:

所以K判据与G判据具有等价关系。临界能量释放率可由下式计算

2 分形裂纹弯折效应下的岩石断裂韧性
由分形理论可知,分形裂纹曲线处处不可微,这意味着分形裂纹处处有拐点,且呈弯折状沿着主方向扩展。国内外学者研究发现,即使在Ⅰ型加载下分形裂纹弯折扩展也会引起裂纹顶端的局部复合型加载[19],对于线弹性材料,裂纹顶端附近的应力场可由局部应力强度因子kⅠ,kⅡ和kⅢ来表示,而局部应力强度因子是由裂纹几何尺寸和表观应力强度因子KⅠ,KⅡ和KⅢ所决定的[17]。由于水力裂缝为Ⅰ型加载情况下产生的裂纹,下面只谈论Ⅰ型裂纹扩展下岩石的应力强度因子。如果Ⅰ型裂纹的扭转效应可忽略不计,则由断裂理论可知[17]:
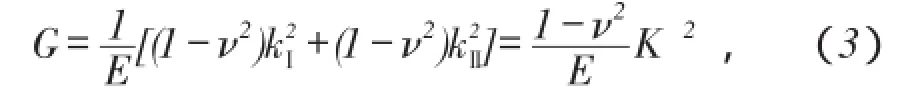
式中

图1为分形裂纹扩展模型。利用断裂理论可得其局部应力强度因子kI和kII[17]为
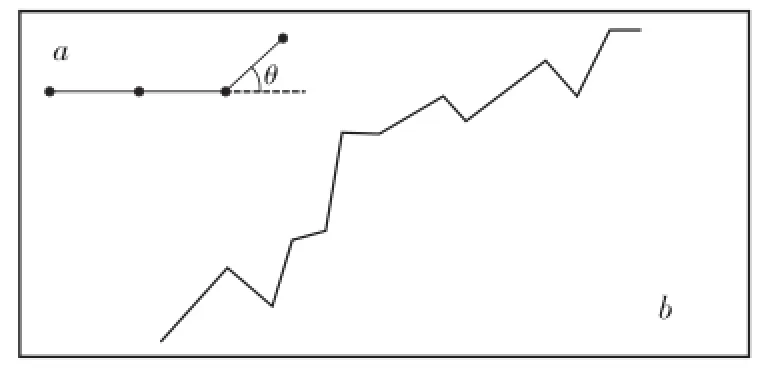
图1 分形弯折裂纹模型
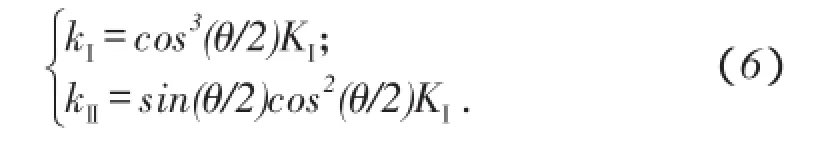
由(4)式和(6)式得
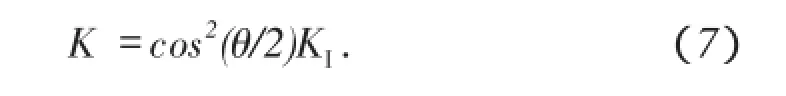
联立(1)式、(2)式、(3)式和(7)式得
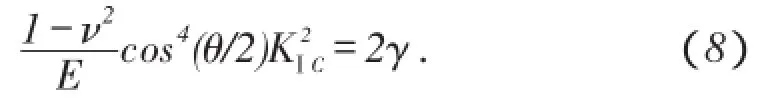
3 分形裂纹长度效应下的岩石断裂韧性
经典断裂力学认为岩石断裂面是光滑的,实际上无论是在宏观层面还是微观层面,岩石断面都是粗糙不规则的,所以水力裂缝壁面实际上是凹凸不平的,具有粗糙性,这种粗糙性明显增加了裂缝表面面积。设宏观断裂面积为A宏,实际断裂面积为A实,则A实大于A宏。考虑裂缝平直扩展时的长度为L0,而裂缝分形扩展的实际长度为L(δ),由此可得[17]

由(2)式和(9)式可得裂缝分形扩展下的临界能量释放率

Mandelbort的分形曲线长度计算公式[15]为

由(10)式和(11)式得

由(1)式和(12)式得

由(8)式和(13)式得

根据图1所示的分形裂纹模型和分形理论可得[19]
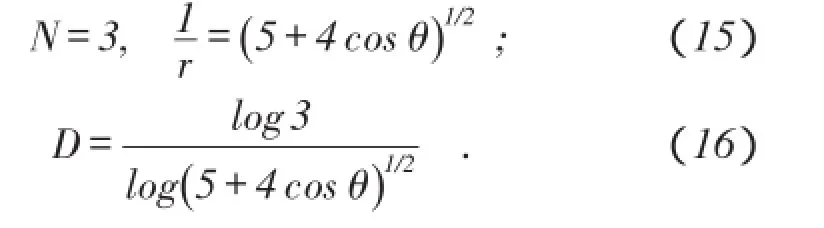
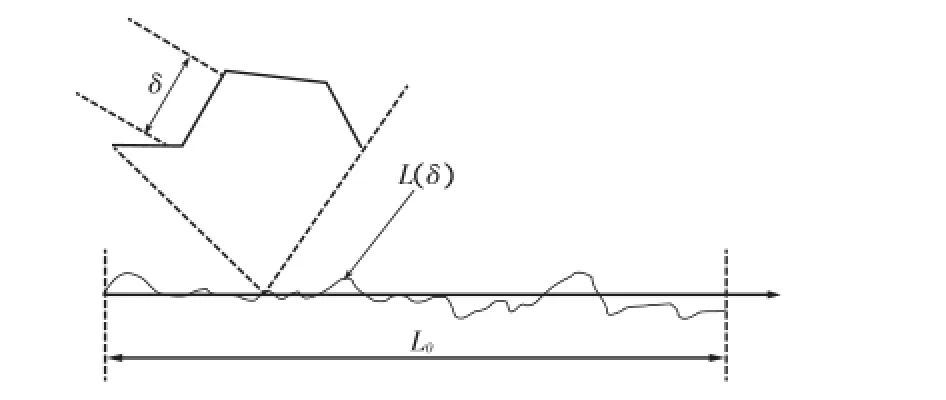
图2 水力裂缝分形扩展模型
由(14)式、(15)式和(16)式得
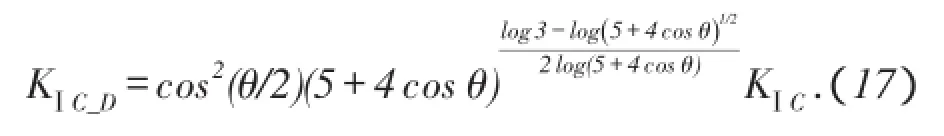
4 分形效应对缝内净压力和裂缝形态的影响
无限大地层中存在一条长度为2L的水力裂缝(图3)。假设水力裂缝内流体压力均匀分布,在不考虑分形效应的情况下,由断裂理论可知[18]:


图3 水力裂缝坐标示意
实际水力裂缝扩展过程中具有分形效应,由文献[10]可知:
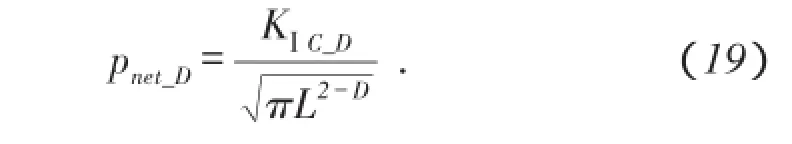
结合(17)式、(18)式和(19)式可知:

由文献[19]和文献[20]可知,在假设水力裂缝扩展为线性扩展的条件下,缝宽方程为
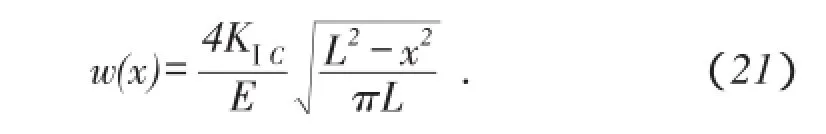
借鉴文献[15]和文献[21]中关于水力裂缝缝宽方程的推导思路,并结合(14)式,可得出考虑分形裂纹弯折效应和长度效应下水力裂缝缝宽方程为

结合(15)式、(17)式和(22)式可得

(23)式就是考虑水力裂缝分形扩展长度效应和弯折效应条件下的缝宽方程。由(23)式可知,水力裂缝宽度与缝内净压力无关,而与岩石杨氏模量、岩石断裂韧性、分形维数有关。
在实际应用中,可在实验室测得KⅠC[22],并通过室内岩心断裂实验、电镜扫描岩石断裂面,计算分形维数以及裂缝扩展弯折角,为后续压裂计算提供基本参数。
5 影响因素分析
水力裂缝扩展过程中的分形效应是客观存在的,忽略分形效应而建立的水力压裂模型必然存在理论误差。分析和研究分形效应对水力裂缝扩展的影响,不仅能够更加精确地预测水力裂缝扩展过程中缝内净压力和裂缝形态,而且还能优化施工参数,使得支撑剂粒径选择更加合理。
5.1分形效应对裂缝扩展净压力的影响
由(16)式可知,分形维数与弯折角一一对应,根据(16)式作出分形维数与弯折角的关系图(图4)。由图4可知,弯折角越大,分形维数越大,说明裂缝扩展越曲折,分形维数越大,裂缝壁面越粗糙。由(20)式可知,净压力比值与裂缝弯折角和裂缝宏观长度有关。根据(20)式作出净压力比值与裂缝弯折角和裂缝宏观长度的关系图(图5)。由图5可知,弯折角越大,裂缝扩展所需净压力越大,即所需施工压力越大。对于给定储集层岩石,即裂缝扩展弯折角给定条件下,净压力比值随着裂缝宏观长度的增加而增大。

图4 分形维数与弯折角的关系

图5 不同假设条件下净压力比值随弯折角的变化
5.2分形效应对裂缝宽度的影响
根据(21)式和(23)式作出裂缝宽度比值随分形维数的变化图(图6)。由图6可知,与裂缝线性扩展模型相比,裂缝分形扩展模型计算得到的缝宽在裂缝的前80%部分是减小的,只有在靠近裂缝端部缝宽是增加的。即用线性扩展模型得到的缝宽较实际情况偏大,所以线性扩展模型中能够安全通过的支撑剂在实际情形可能形成桥堵。

图6 分形维数对裂缝不同位置处缝宽比的影响
6 结论与建议
(1)水力裂缝在扩展过程中具有分形特征,在进行计算时,既要考虑分形裂纹的长度效应,又要考虑分形裂纹的弯折效应。
(2)与水力裂缝线性扩展模型相比,考虑裂缝的分形长度效应和弯折效应后,水力裂缝扩展所需要的缝内净压力更大。
(3)与裂缝线性扩展模型相比,裂缝分形扩展模型计算得到的缝宽在裂缝的前80%部分是减小的,只有在靠近裂缝端部缝宽是增加的。即用线性模型算出的缝宽较实际情况偏大,所以线性模型中能够安全通过的支撑剂在实际中可能形成桥堵。
(4)本文仅研究了分形裂纹长度效应和弯折效应对水力裂缝扩展的影响,建议进一步研究裂缝分形效应对支撑剂运移和沉降的影响。
符号注释
A
宏——宏观层面断裂表面积,m2;
A实——实际断裂表面积,m2;
D——线分形维数;
E——岩石弹性模量,GPa;
G——能量释放率;
GC——临界能量释放率;
GC_D——裂缝分形扩展下的临界能量释放率;
K——裂纹的应力强度因子,MPa·m1/2;
K*——考虑裂纹弯折效应所对应的应力强度因子,MPa·m1/2;
KⅠ——常规断裂力学中定义的纯Ⅰ型裂纹的应力强度因子,MPa·m1/2;
KⅠC_D——储集层中水力裂缝的实际断裂韧性,MPa·m1/2;
KⅠC——实验室测得的岩石断裂韧性,MPa·m1/2;
kⅠ——Ⅰ型局部应力强度因子,MPa·m1/2;
kⅡ——Ⅱ型局部应力强度因子,MPa·m1/2;
L——水力裂缝半长,m;
L0——裂缝平直扩展时的长度,m;
L(δ)——裂缝分形扩展时的实际长度,m;
N——生成元的折线段数;
pnet——不考虑分形效应下裂缝扩展所需的缝内净压力,MPa;
pnet_D——考虑分形效应下裂缝扩展所需的缝内净压力,MPa;
r——分形相似比;
w(x)——裂缝线性扩展下在x处的水力裂缝宽度m;
w(x)D——裂缝分形扩展下在x处的水力裂缝宽度m;
x——距离裂缝根部的距离,m;
ν——岩石泊松比;
γ——单位宏观量度断裂面积表面能,kJ/m2;
θ——分形裂纹扩展的弯折角,(°)。
[1]谢和平.脆性材料裂纹扩展的分形运动学[J].力学学报,1994,26(6):757-762. Xie Heping.Fractal kinematics of crack propagation in brittle materi⁃alls[J].ActaMechanicaSinica,1994,26(6):757-762.
[2]赵顺超,罗志锋,袁学芳,等.裂缝性致密砂岩储集层酸压增产机理[J].新疆石油地质,2014,35(2):208-210. Zhao Shunchao,Luo Zhifeng,Yuan Xuefang,et al.Stimulation mechanism of acid fracturing in fractured tight sandstone reservoirs[J]XinjiangPetroleum Geology,2014,35(2):208-210.
[3]孙洪泉,谢和平.岩石断裂表面的分形模拟[J].岩土力学,2008,29(2):347-352. Sun Hongquan,Xie Heping.Fractal simulation of rock fracture sur⁃face[J].Rock and Soil Mechanics,2008,29(2):347-352.
[4]郑山锁,任梦宁,谢明,等.混凝土断裂面多重分形谱的二次拟合研究[J].工程力学,2013,30(5):97-102. Zheng Shansuo,Ren Mengning,Xie Ming,et al.Study on quadratic fitting of multi⁃fractal spectrum of fracture surface in concrete[J]. EngineeringMechanics,2013,30(5):97-102.
[5]罗攀,李勇明,江有适,等.砂砾岩水力裂缝延伸路径模拟研究[J].油气地质与采收率,2013,20(5):103-106. Luo Pan,Li Yongming,Jiang Youshi,et al.Research on micro⁃mor⁃phology characteristics of hydraulic fractures for conglomerate reser⁃voir[J].Petroleum Geology and Recovery Efficiency,2013,20(5): 103-106.
[6]李连崇,李根,孟庆民,等.砂砾岩水力压裂裂缝扩展规律的数值模拟分析[J].岩土力学,2013,34(5):1 501-1 507. Li Lianchong,Li Gen,Meng Qingmin,et al.Numerical simulation of propagation of hydraulic fractures in glutenite formation[J].Rock and Soil Mechanics,2013,34(5):1 501-1 507.
[7]衡帅,杨春和,曾义金,等.页岩水力压裂裂缝形态的试验研究[J].岩土工程学报,2014,36(7):1 243-1 251. Heng Shuai,Yang Chunhe,Zeng Yijin,et al.Experimental study on hydraulic fracture geometry of shale[J].Chinese Journal of Geotech⁃nical Engineering,2014,36(7):1 243-1 251.
[8]陈勉,周健,金衍,等.随机裂缝性储层压裂特征实验研究[J].石油学报,2008,29(3):431-434. Chen Mian,Zhou Jian,Jin Yan,et al.Experimental study on fractur⁃ing features in naturally fractured reservoir[J].Acta Petrolei Sinica,2008,29(3):431-434.
[9]周健,陈勉,金衍,等.多裂缝储层水力裂缝扩展机理试验[J].中国石油大学学报:自然科学版,2008,32(4):51-54. Zhou Jian,Chen Mian,Jin Yan,et al.Experiment of propagation mechanism of hydraulic fracture in multi⁃fracture reservoir[J].Jour⁃nal of ChinaUniversity of Petroleum:Natural Science Edition,2008,32(4):51-54.
[10]张杨,袁学芳,闫铁,等.水力裂缝分形扩展对压裂效果的影响[J].石油钻探技术,2013,41(4):101-104. Zhang Yang,Yuan Xuefang,Yan Tie,et al.Influence of hydraulic fracture fractal propagation on fracturing result[J].Petroleum DrillingTechniques,2013,41(4):101-104.
[11]Goldshtein R V,Mosolov A B.Fractal cracks[J].Journal Applied Mathematics and Mechanics,1992,56(4):563-571.
[12]Yavari A.Generalization of barenblatts conhesive fracture theory for fractal cracks[J].World Scientific,2002,10(2):189-198.
[13]屈展.水力压裂裂缝的分形(fractal)几何描述[J].石油学报,1993,14(4):91-98. Qu Zhan.The description of hydraulic fracturing crack by the frac⁃tal geometry[J].ActaPetrolei Sinica,1993,14(4):91-98.
[14]刘洪,符兆荣,黄桢,等.水力压裂力学机理新探索[J].钻采工艺,2006,29(3):36-39. Liu Hong,Fu Zhaorong,Huang Zhen,et al.Study on hydraulic fracturing mechanics[J].Drilling&Production Technology,2006, 29(3):36-39.
[15]李玮,闫铁,毕雪亮.基于分形方法的水力压裂裂缝起裂扩展机理[J].中国石油大学学报:自然科学版,2008,32(5):87-91. Li Wei,Yan Tie,Bi Xueliang.Mechanism of hydraulically created fracture breakdown and propagation based on fractal method[J]. Journal of China University of Petroleum:Natural Science Edition, 2008,32(5):87-91.
[16]李玮,闫铁.分形岩石力学及其在石油工程中的应用[M].北京:石油工业出版社,2012. Li Wei,Yan Tie.Fractal rock mechanics and its application in pe⁃troleum engineering[M].Beijing:Petroleum Industry Press,2012.
[17]谢和平.分形-岩石力学导论[M].北京:科学出版社,1997. Xie Heping.Introduction to fractal⁃rock mechanics[M].Beijing: Science Press,1997.
[18]范天佑.断裂理论基础[M].北京:科学出版社,2003:11-80. Fan Tianyou.Fracture theory basis[M].Beijing:Science Press, 2003:11-80.
[19]谢和平,Sanderson D J.动态裂纹扩展中的分形效应[J].力学学报,1995,27(1):18-27. Xie Heping,Sanderson D J.Fractal effects of dynamic crack propa⁃gation[J].ActaMechanicaSinica,1995,27(1):18-27.
[20]陈勉,金衍,张广清.石油工程岩石力学[M].北京:科学出版社,2008:164-164. Chen Mian,Jin Yan,Zhang Guangqing.Rock mechanics for petro⁃leum engineering[M].Beijing:Science Press,2008:164-164.
[21]阳友奎,肖长富,邱贤德,等.水力压裂裂缝形态与缝内压力分布[J].重庆大学学报,1995,18(3):20-26. Yang Youkui,Xiao Changfu,Qiu Xiande,et al.Fracture geometry and pressure distribution in fracture for hydraulic fracturing[J]. Journal of ChongqingUniversity,1995,18(3):20-26.
[22]楼一珊,陈勉,史明义,等.岩石Ⅰ、Ⅱ型断裂韧性的测试及其影响因素分析[J].中国石油大学学报:自然科学版,2007,31(4):85-89. Lou Yishan,Chen Mian,Shi Mingyi,et al.Measurement of type⁃Ⅰand type⁃Ⅱfracture toughness for rocks and its influence factors analysis[J].Journal of China University of Petroleum:Natural Sci⁃ence Edition,2007,31(4):85-89.
Mechanism of Hydraulic Fracture Propagation Considering Fractal Crack Length and Bending Effects
LI Xiaogang1,YI Liangping1,YANG Zhaozhong1,ZHOU Nayun2
(1.State KeyLaboratoryofOilandGas ReservoirGeologyandExploitation,SouthwestPetroleumUniversity,Chengdu,Sichuan 610500,China; 2.ResearchInstitute ofGas ProductionEngineering,SouthwestOil&Gas FieldCompany,PetroChina,Guanghan,Sichuan 618300,China)
To well understand the impact of fractal cracks propagation on hydraulic fracturing,the fracture toughness expressions consider⁃ing the fractal crack length and bending effects were re⁃derived based on traditional linear fracture expansion model,establishing a new equation for hydraulic fracture width and the model for crack internal net pressure as required by hydraulic fracture propagation.Theoreti⁃cal analysis indicates that the fractal dimension increases with crack propagation bending angle.Compared with the linear fracture expan⁃sion model,the crack internal net pressure is increasing after considering the fractal crack length and bending effects,and the fracture width given by this linear model is decreasingin the first 80%part of a fracture,that is,the fracture width near the fracture end could be in⁃creasing,which means that the fracture width computed by the linear fracture expansion model will be bigger than that in actual condition. Subsequently,the proppants available for fracture propagation in the linear model may possibly form bridge pluggingin practice.
hydraulic fracturing;fractal crack propagation;bendingeffect;fracture width equation;fracture toughness
TE357.11
A
1001-3873(2015)04-0454-05
10.7657/XJPG20150413
2014-12-12
2015-04-13
国家自然科学基金(U1262209);国家科技重大专项(2011ZX05042-002-001)
李小刚(1981-),男,四川仁寿人,副教授,博士,油气田开发,(Tel)028-83032050(E-mail)swpuadam@126.com.

