龙船花两变种叶面积回归方程的建立
李碧洳,翁殊斐,冯嘉仪,欧泳欣
(华南农业大学 林学与风景园林学院,广东 广州 510642)
龙船花两变种叶面积回归方程的建立
李碧洳,翁殊斐,冯嘉仪,欧泳欣
(华南农业大学 林学与风景园林学院,广东 广州 510642)
以龙船花两变种橙红龙船花Ixora coccinea var. coccinea、邦德胡卡红仙丹草I. coccinea var. bandhuca的成熟叶为材料,利用WinFolia软件测定多项叶形态指标,并对叶面积进行回归分析,分别建立其8种回归方程以及总的适用回归方程。结果表明,龙船花两变种的叶片长×叶水平宽、叶周长、叶垂直长、叶片长、叶水平宽、叶片长×叶片长以及叶水平宽×叶水平宽与叶面积之间的相关系数及复相关系数均呈极显著水平(P<0.01),可分别用来建立龙船花的叶面积回归方程;叶面积与叶片长×叶水平宽的相关系数及复相关系数最高,基于叶片长×叶水平宽的8种叶面积回归方程更好地估测两种龙船花的叶面积。经检验发现,二次函数、复合函数、幂函数能更准确地估测叶面积;由两种龙船花共同建立的3种总的回归方程中,复合函数与幂函数能更好地模拟估测叶面积。
橙红龙船花;邦德胡卡红仙丹草;叶面积;回归方程
龙船花属Ixora是茜草科第二大属,约有300~400种,多数种类分布于亚洲热带以及非洲和大洋洲[1]。常绿灌木或小乔木,叶常对生,伞房花序或聚伞花序,小花颜色鲜艳多样,花期几乎全年,但夏秋季为盛花期,部分种具香气,是观赏价值较高的木本花卉[2—3],常丛植、群植、孤植、列植配置于公园、居住区等,亦可盆栽于室内观赏[4]。
叶片是植物进行光合作用和蒸腾作用等生理过程的重要器官,叶面积大小与植物的生理活动以及生长发育有着密切联系。同时,叶面积作为叶片结构型性状之一,能较好地反映植物的生存适应策略,农业、林业、生态学等研究中将叶面积以及与其相关的比叶面积、叶面积指数作为常用指标[5—8]。目前,测定叶面积的方法有多种,主要包括求积仪法、方格法、数字图像处理法、称重法、回归分析法与系数法等[9]。其中,回归分析法具有简单、非破坏性、可活体测量的特点而受到广泛关注。近年来,关于叶面积回归分析的研究多以乔木为主[10—11],而对于常见的园林灌木和地被的研究相对较少。本研究通过对华南地区常用的园林植物橙红龙船花Ixora coccinea var. coccinea、邦德胡卡红仙丹草I. coccinea var. bandhuca进行叶面积回归分析,以期建立适用于两种龙船花可靠的叶面积回归方程,为今后龙船花属植物的生产、生理等科研实践提供简单有效的叶面积测算方法。
1 材料与方法
1.1材料
试材为华南农业大学校园绿地中的橙红龙船花和邦德胡卡红仙丹草。选取健康无病害的植株,随机抽取自上往下第4~7片成熟叶片各100片,用湿布包裹装入保鲜袋。
1.2方法
每种龙船花随机选取80个叶样用于回归分析,利用WinFolia软件分别测定每种叶形态指标,包括叶面积(LA)、叶周长(LP)、叶垂直长(VL,叶尖至叶柄基部的最大长度)、叶片长(L,叶尖至叶片基部的垂直长度)、叶水平宽(W,与主脉垂直的叶片最大宽度),并计算叶片长×叶水平宽(LW)、叶水平宽×叶水平宽(WW)、叶片长×叶片长(LL)、叶片长/叶水平宽(L/W)等指标。
运用Excel统计数据,利用SPSS 21.0软件对数据进行分析,对龙船花两变种叶面积与上述9个叶形指标的相关性进行分析,建立一元线性方程、对数函数、逆函数、二次方、三次方、复合函数、幂函数、指数函数等8种常见回归方程,并分别用剩余的20片叶样进行检验;选出适用的总的回归方程。
2 结果与分析
2.1叶形指标及样本差异
邦德胡卡红仙丹草的叶面积、叶周长、叶垂直长、叶片长以及叶水平宽的均值比橙红龙船花的对应指标的数值大,其中叶面积的差异最为明显(表1),其次为叶周长。分别对两者的叶面积、叶周长、叶垂直长、叶片长、叶水平宽以及叶片长/叶水平宽等叶形指标进行差异性检验,P值均小于0.01,说明两者各项上述叶形指标差异极显著。

表1 龙船花两变种植物叶形指标Table 1 Leaf indices of two varieties of Ixora coccinea
2.2叶形指标相关性分析
橙红龙船花的叶面积与各叶形指标间的相关性极显著,除叶片长/叶水平宽与叶面积存在负相关性外,其余指标与叶面积均呈正相关(表2)。邦德胡卡红仙丹草除了叶片长/叶水平宽与叶面积的相关性不显著,不能作为建立叶面积回归方程的参考指标外,其余指标与叶面积的相关性均极显著。
龙船花两变种的叶形指标与叶面积的相关程度从高到低依次为叶片长×叶水平宽、叶水平宽、叶水平宽×叶水平宽、叶周长、叶片长×叶片长、叶片长、叶垂直长;而叶垂直长/叶水平宽、叶片长/叶水平宽与叶面积的相关性最低。结果显示,两种龙船花的叶面积与叶片长×叶水平宽、叶周长、叶垂直长、叶片长、叶水平宽、叶片长×叶片长以及叶水平宽×叶水平宽之间均可建立较好的回归方程。

表2 龙船花两变种叶面积与其他叶形态测量指标相关性分析Table 2 Pearson correlation analysis between leaf area and other leaf indices of two varieties of Ixora coccinea
2.3叶面积回归方程建立
以相关性较高且极显著的 7个叶形指标对两种龙船花的叶面积进行一元线性方程、对数函数、逆函数、二次方、三次方、复合函数、幂函数、指数函数等8种常见回归方程回归分析。
橙红龙船花基于叶周长、叶垂直长、叶片长、叶水平宽、叶片长×叶水平宽、叶片长×叶片长、叶水平宽×叶水平宽等 8种叶面积回归方程对叶面积实测值均呈极显著相关(P<0.01),R2分别为0.810~0.872、0.714~0.782、0.725~0.803、0.842~0.889、0.894~0.983、0.694~0.809、0.802~0.890;邦德胡卡红仙丹草基于叶周长、叶垂直长、叶片长、叶水平宽、叶片长×叶水平宽、叶片长×叶片长、叶水平宽×叶水平宽的8种叶面积回归方程的R2分别为0.835~0.904、0.793~0.870、0.809~0.880、0.881~0.902、0.940~0.992、0.774~0.880、0.868~0.902。结果显示,以各种叶形指标建立两种龙船花的叶面积回归方程的R2值都较高,拟合效果较好,但以叶片长×叶水平宽为自变量的叶面积回归方程的R2最高(表3),拟合效果最好。说明以叶片长×叶水平宽为指标建立的叶面积方程更准确可靠。

表3 两变种龙船花的基于叶片长×叶水平宽的叶面积回归方程Table 3 Leaf area regression equations of two varieties of Ixora coccinea based on leaf blade length×leaf horizontal wide
2.4基于叶片长×叶水平宽的叶面积回归方程检验
将剩余20片叶样的叶片长×叶水平宽值分别代入8种回归方程中(表3),计算出叶面积估测值,对计算结果进行可靠性检验(表4)。
橙红龙船花、邦德胡卡红仙丹草的8种回归方程测定的估测值与实测值的P值均大于0.05,证明8种回归方程的估测值与实测值之间差异性不显著;用LSD多重比较分别对两种龙船花的8种回归方程估测值的均值进行比较,差异不显著(P >0.05)。说明橙红龙船花、邦德胡卡红仙丹草基于叶片长×叶水平宽的 8种回归方程都能较好地估测叶面积。橙红龙船花的对数函数、逆函数、三次方程与复合函数的叶面积实测值与估测值差值为正值,表明回归方程估测的叶面积平均值要小于实际测定值,一元线性方程、二次方程、幂函数、指数函数方程的叶面积差值为负值,表明回归方程计算的叶面积平均值要大于实测值;橙红龙船花叶面积的估测值与实测值的平均差值与差异率由小到大为:对数函数 <幂函数 < 二次方程 < 复合函数 < 一元线性方程 < 逆函数 < 三次方程 < 指数函数。邦德胡卡红仙丹草的8种方程叶面积的实测值与估测值差值为负值,表明8种回归方程估测的叶面积平均值要小于实际测定值;邦德胡卡红仙丹草叶面积的估测值与实测值的差值与差异率由小到大为:二次方程 < 复合函数 < 幂函数 < 一元线性方程 < 三次方程 < 指数函数 < 对数函数 < 逆函数。可发现,两种龙船花的二次方程、复合函数、幂函数的估测值与实测值差异较小,能较好地估测叶面积。
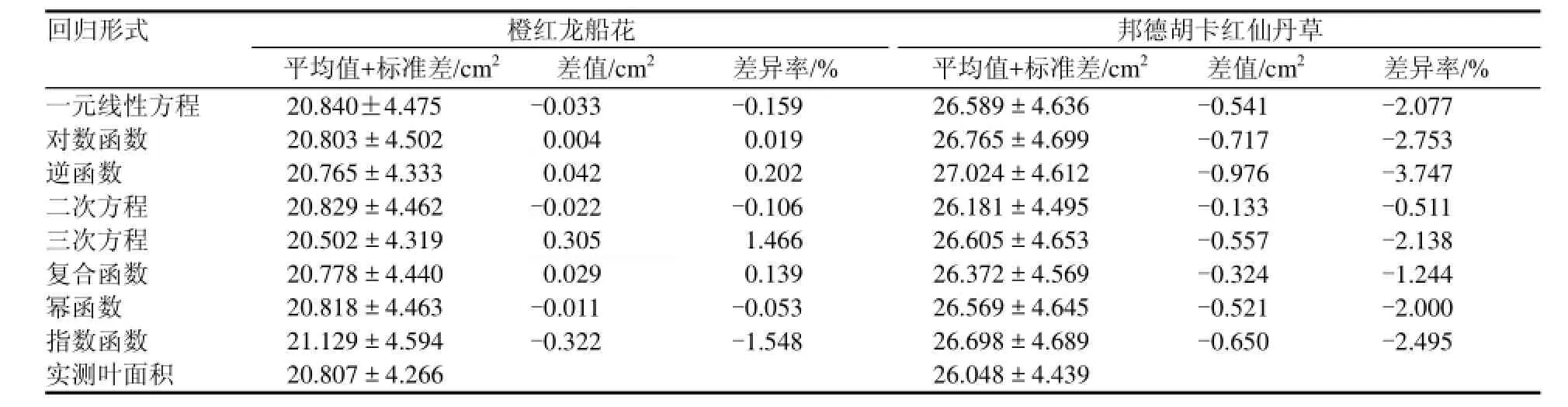
表4 龙船花两变种叶面积实测值与基于叶片长×叶水平宽回归方程估测值比较Table 4 The comparison of actual leaf area and estimated leaf area based on leaf blade length×leaf horizontal wide of two varieties of Ixora coccinea
2.5适合龙船花两变种的叶面积回归方程分析与检验
以橙红龙船花、邦德胡卡红仙丹草用作叶面积回归分析的160片叶片进行总的叶面积回归分析,建立幂函数LA= 0.725(LW)1.005(R2= 0.991)、二次方程LA= -0.240 + 0.748LW - 0.0001(LW)2(R2= 0.993)、复合函数LA= 9.030(1.029LW) (R2= 0.968)。3种总的叶面积回归方程与两种龙船花的叶面积均极显著相关(P<0.01)。分别用两种龙船花剩下的各20片叶样的实测值与总的叶面积方程估测值进行可靠性检验(表5),经差异性检验发现,橙红龙船花、邦德胡卡红仙丹草的叶面积实测值与3种总的叶面积回归方程的估测值均不存在显著差异性(P>0.05);用LSD多重比较分别对两种龙船花的3种总的回归方程的估测值均值进行比较,均不存在显著差异性(P>0.05)。
邦德胡卡红仙丹草的实测值与估测值的平均差值、差异率均比橙红龙船花大,说明总的回归方程用于估测橙红龙船花的叶面积更准确。总体上 3种方程的估测值与实测值之间差异较小,均可用于估测两种龙船花的叶面积,但总的复合函数与幂函数的估测值与实测值的平均差值与差异率比二次方程的小,说明总的复合函数与幂函数用于估测两种龙船花的叶面积比二次方程更准确。橙红龙船花叶面积的实测值与幂函数方程的估测值之间的差异比复合函数小,邦德胡卡红仙丹草叶面积的实测值与复合函数的估测值的差异比幂函数小,说明幂函数方程用于估测橙红龙船花的叶面积更精确,而复合函数用于估测邦德胡卡红仙丹草的叶面积更精确。

表5 两变种龙船花叶面积实测值与总回归方程估测值比较Table 5 The comparison of actual leaf area and estimated leaf area of regression equation both suitable for two varieties of Ixora coccinea
3 讨论
3.1叶形态指标比较
邦德胡卡红仙丹草的叶面积、叶周长、叶垂直长、叶片长和叶水平宽的均值均比橙红龙船花的大。两种龙船花的叶面积、叶周长、叶垂直长、叶片长、叶水平宽以及叶片长/叶水平宽等叶形指标之间的差异极显著(P<0.01)。随着栽培技术的发展,龙船花属的种类、品种、变种及变型越来越多,更新速度快,给分类与鉴别工作带来较大困难,也阻碍了龙船花属相关研究的进展。叶片长、叶水平宽以及叶片长/叶水平宽是植物形态分类学重要指标,两种龙船花叶形指标之间的显著差异可为辨认植物以及龙船花属的分类提供参考。
龙船花两变种的叶周长、叶垂直长、叶片长、叶水平宽、叶片长×叶水平宽、叶片长×叶片长以及叶水平宽×叶水平宽与叶面积均表现出显著正相关,说明这些叶形指标皆可作为叶面积无损测定的自变量,但考虑到叶周长在实测中需要用到特定的工具或仪器才能测得,相比于叶片长、叶水平宽等指标较难测量,故不建议在实际应用中将叶周长作为建立叶面积回归方程的指标[12]。
3.2叶面积回归方程的建立与应用
研究表明,龙船花两变种基于叶周长、叶垂直长、叶片长、叶水平宽、叶片长×叶水平宽、叶片长×叶片长以及叶水平宽×叶水平宽等7个叶形态指标建立的一元线性方程、对数函数、逆函数、二次方程、三次方程、复合函数、幂函数、指数函数等 8种回归方程均可用于叶面积回归测算。两种龙船花基于叶片长×叶水平宽的8种叶面积回归方程的复相关系数R2在0.890以上,拟合效果最好,这与前人的研究相似[13—14]。因此,叶片长×叶水平宽可作为叶面积无损测定优先选择的模型指标。
本研究发现,橙红龙船花基于叶片长×叶水平宽的对数函数、幂函数、二次方程、复合函数,以及邦德胡卡红仙丹草的二次方程、复合函数、幂函数、一元线性方程估测两者叶面积的精确度较高,这说明不同变种的最适方程各不相同,建立叶面积方程时应各自进行全面的分析,使建立的回归方程预测结果更准确。用龙船花两变种的叶片样本共同建立的、基于叶片长×叶水平宽的复合函数、幂函数、二次方程等 3种叶面积回归方程,均可用于估测两种龙船花的叶面积,但总的复合函数、幂函数估测叶面积的误差更小,比二次方程更准确。本研究结果与前人关于火棘、雷公藤等以幂函数为最佳拟合方程的结论有一定的相似性[13,15],但也略有不同,这可能是不同植物的不同叶形态所建立最适回归方程类型不一样的原因。本研究所提出的回归方程适用于橙红龙船花与邦德胡卡红仙丹草,但是否适用于龙船花属的其他种类,还需进一步验证。
龙船花两变种各自建立的基于叶片长×叶水平宽的8种回归方程,以及由两者叶片共同建立的基于叶片长×叶水平宽的二次方程、复合函数、幂函数3种总的叶面积回归方程,经检验发现其估测值与叶面积实测值没有显著差异,且平均差值与差异率较小,都可用于估测各自的叶面积,在实际应用中可根据精度需要、工作量以及计算难易程度选用。
[1] 中国科学院中国植物志编辑委员会. 中国植物志(第71卷第2分册)[M]. 北京: 科学出版社, 1999: 30—45.
[2] 陆銮眉,林金水,张亚兰,杜晓娜,卢伟志. 6 种龙船花的光合特性研究[J]. 热带作物学报, 2010,31(10): 1736—1742.
[3] 唐玉贵. 龙船花新品种及其栽培技术[J]. 广西林业科学, 2002,31(2): 101—102.
[4] 李颖欣,翁殊斐,张波. 龙船花属(Ixora)植物研究现状及其园林应用[J]. 热带农业科学, 2013(1): 96—101.
[5] 周鹏,翁殊斐,杭夏子. 5种龙船花属植物幼苗生长与生物量的研究[J]. 西北林学院学报, 2014(3): 75—78.
[6] 李仙岳,杨培岭,任树梅,张少炎. 基于叶面积与冠层辐射的果树蒸腾预测模型[J]. 生态学报, 2009,29(5): 2312—2319.
[7] 刘金环,曾德慧,Lee D K. 科尔沁沙地东南部地区主要植物叶片性状及其相互关系[J]. 生态学杂志, 2006,25(8): 921—925.
[8] 黄文娟,李志军,杨赵平,白冠章. 胡杨异形叶结构型性状及其相互关系[J]. 生态学报, 2010(17): 4636—4642.
[9] 柏军华,王克如,初振东,陈兵,李少昆. 叶面积测定方法的比较研究[J]. 石河子大学学报(自然科学版), 2005(2): 216—218.
[10] 谢安德,王凌晖,潘启龙. 灰木莲叶面积回归方程的建立[J]. 广东农业科学, 2011(14): 28—29,32.
[11] 陈宗礼,雷婷,齐向英,王晓涧,张向前,刘世鹏,薛皓. 20个品种枣树叶面积回归方程的建立[J]. 生物学杂志, 2013(1): 86—90.
[12] 柯娴氡,周庆,苏志尧. 我国南方四种植物的叶面积无损测定[J]. 广东林业科技, 2009(6): 39—44.
[13] 王勇,杜晓军,招礼军,焦志华,安明态. 五种火棘属植物的叶面积回归分析[J]. 广西植物, 2013(6): 756—762.
[14] Pompelli M F, Antunes W C, Ferreira D T R G, Cavalcante P G S, Wanderley-Filho H C L, Endres L. Allometric models for non-destructive leaf area estimation of Jatropha curcas[J]. Biomass Bioenergy, 2012,36: 77—85.
[15] 涂育合. 雷公藤叶面积回归方程法测算[J]. 西南林学院学报, 2007(4): 16—19.
Regression Equation of Leaves Area on Two Varieties of Ixora coccinea
LI Bi-ru, WENG Shu-fei, FENG Jia-yi, OU Yong-xin (College of Forestry and Landscape Architecture, South China Agricultural University, Guangzhou 510642, Guangdong China)
Quick and non-destructive methods for estimating leaf area were important for future related research of Ixora. In order to estimate leaf area of two varieties of Ixora, mature leaves of I. coccinea var. coccinea and I. coccinea var. bandhuca were collected as the experiment materials. The WinFolia software was used to measure leaf shape indices such as leaf area(LA), leaf perimeter(LP), leaf vertical length(VL), leaf blade length(L), leaf horizontal width(W), LW, LL, WW, and L/W. The respective regression analysis between leaf area and other leaf shape indices of the varieties of Ixora were carried out by using 8 common regression models. Besides, the general regression equation that suitable for two Ixora varieties were established. The results indicated that the correlation and the multiple correlation coefficients between the leaf area and the leaf shape indices,such as LW, LP, VL, L, W, LL, and WW, were at extremely significant level (P<0.01); the correlation and the multiple correlation coefficients between the leaf area and LW were the highest, respectively; leaf area could be predicted better with LW by quadratic function, composite function and power function; among the three kinds of regression equations that both suitable for two Ixora varieties, the composite function and power function could be better to predict leaf area.
Ixora coccinea var. coccinea; Ixora coccinea var. bandhuca; leaf area; regression equation
10.3969/j.issn.1009-7791.2015.03.008
S685.99
A
1009-7791(2015)03-0218-05
2015-05-08
广东省科技计划项目(2013B020302004)
李碧洳,硕士研究生,从事园林植物研究。E-mail: libiru1008@163.com
注:翁殊斐为通讯作者。E-mail: shufeiweng@scau.edu.cn

