泥页岩地层破裂压力计算模型研究

严向阳，胡永全，李楠，申贝贝

（1.美国能新科国际有限公司，成都610000；2.西南石油大学石油与天然气工程学院，成都610500；3.中国石化西北油田分公司工程技术研究院，乌鲁木齐830000；4.中国石化华北油田分公司工程技术研究院，郑州450000）

泥页岩地层破裂压力计算模型研究

严向阳1，胡永全2，李楠3，申贝贝4

（1.美国能新科国际有限公司，成都610000；2.西南石油大学石油与天然气工程学院，成都610500；3.中国石化西北油田分公司工程技术研究院，乌鲁木齐830000；4.中国石化华北油田分公司工程技术研究院，郑州450000）

准确预测压裂井的破裂压力对水力压裂的成功实施具有重要作用。由于存在水化现象，使得泥页岩的岩石力学性质发生变化，从而使泥页岩地层的破裂压力计算与常规地层的破裂压力计算存在一定的差异，因此，不能简单地把常规地层的破裂压力计算方法应用到泥页岩地层中，需要对泥页岩地层破裂压力计算方法进行深入研究。为此，基于弹性力学和岩石力学相关理论，并考虑水化应力对井筒周围应力场的影响，应用最大张应力准则，建立了考虑水化应力计算破裂压力的简单模型，并用此模型结合2种泥页岩水化应力的方法进行实例计算。结果表明，考虑水化应力后比不考虑这一情况的泥页岩地层的破裂压力更接近实际的地层破裂压力。该计算模型为快速预测地层破裂压力提供了依据。

泥页岩；破裂压力；压裂施工；水化应力；水力压裂；岩石力学

0引言

开采页岩油气，水力压裂是必备的技术之一［1-7］。作为水力压裂设计的重要组成部分，破裂压力计算对水力压裂施工具有重要意义。泥页岩地层存在水化现象［8-9］，产生的水化应力使得井筒周围的应力场发生改变［10-11］。应力的改变对井壁的稳定性以及水力压裂都会产生影响，使得泥页岩地层水力压裂与常规地层水力压裂存在一定的差异。目前，国内对泥页岩地层破裂机理方面的研究十分欠缺。因此，为了更好地满足泥页岩储层破裂压力计算的需求，在前人研究的基础上［12］，结合泥页岩水化特征，建立泥页岩储层破裂压力计算新模型，以期为泥页岩储层破裂压力计算提供依据。

1考虑水化应力的破裂压力计算模型

页岩储层的水化效应导致井周围的应力发生变化，从而改变储层的破裂压力。笔者根据弹性力学和岩石力学的相关理论，考虑水化应力对井筒应力场的影响，并根据最大张应力准则，建立了泥页岩地层压裂的破裂压力计算新模型。由于考虑了泥页岩的水化特性，该模型比现有的破裂压力计算模型更能反映泥页岩地层的破裂特征。

1.1井筒应力场模型

垂直井井筒可以看做是平面上的圆孔（图1），对井筒周围的应力分布可以按照矩形平板上的圆孔应力分布进行研究。根据弹性力学的基本原理［13］，井筒周围的应力分布应为［12］

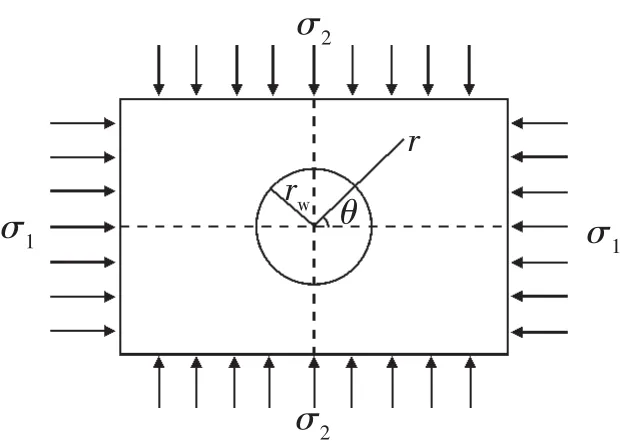
图1矩形平板圆孔周围的应力Fig.1 Stressdistribution around round holeof rectangular plate

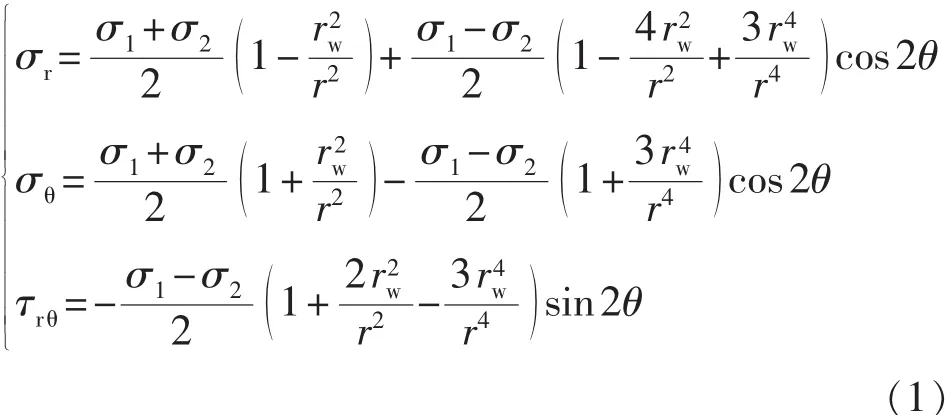
式中：σr，σθ和τrθ分别为径向、周向及剪切的应力，MPa；σ1和σ2分别为水平最大、最小主应力，MPa（这里假设σ1＞σ2）；rw和r分别为井筒和地层任一点半径，m；θ为任意径向与σ1所在轴形成的极角，（°）。

井眼内压引起的应力分量为

液体渗滤引起的切向应力的增加值［13］为

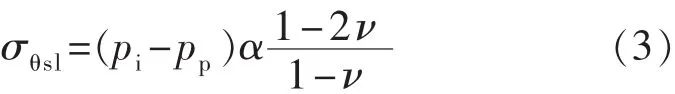
式（2）～（3）中：σθsl为渗滤引起的周向应力增加值，MPa；pi为井筒内压（井底注入压力），MPa；pp为孔隙压力，MPa；α为多孔介质Biot常数，α=1-Cr/Cb；Cr和Cb分别为岩石骨架压缩率和岩石容积压缩率；ν为岩石的泊松比。

由式（1）、式（2）和式（3）可得最终井壁处的周向应力，即

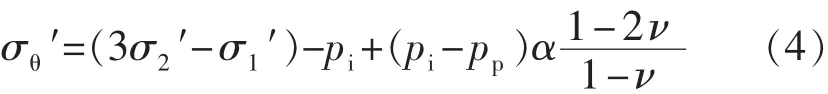
由于地层本身存在孔隙压力pp，因此井壁上的有效周向应力为

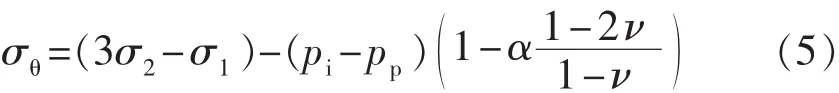
1.2水化应力计算模型

目前，有关泥页岩水化问题，都是针对钻井时的井壁稳定性进行研究的，而水化问题最终都会反映在井壁应力的大小上，因此，这些研究同样也适用于水力压裂的破裂压力计算。

国内外常见的水化应力的计算模型有以下几种：

（1）Chenevert等［14-15］采用的是Marshall提出的计算模型来表述水化应力，这种模型假定泥页岩地层具有半透膜性质，将水化应力当成静水压力来处理，则计算公式为

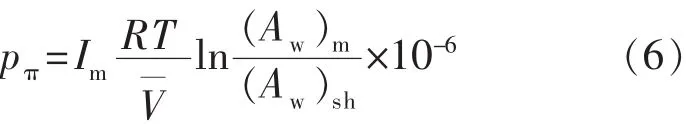
式中：pπ为水化应力，MPa；Im为透膜效率；R为气体常数，8.314 J·mol-1·K-1；T为绝对温度，K；V为纯水偏摩尔体积，m3·mol-1；（Aw）m和（Aw）sh分别为进入液体和页岩的活度。

（2）Tan等［16-17］应用膨胀岩土工程材料增量弹性理论来研究水化膨胀和水化应力，认为水化膨胀会影响基质（有效）应力。按照这种思路，他们通过有效应力和给定应力下的体积改变系数表示出水化引起的体积改变，然后利用刚度矩阵求解出水化应力，即

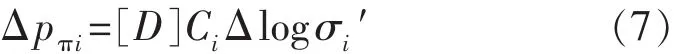
式中：［D］为刚度矩阵；Ci为i方向给定应力下的体积改变系数；σi′为i方向有效应力，MPa。

（3）Huang［18］提出了水化应力计算模型，这种模型的计算公式为?

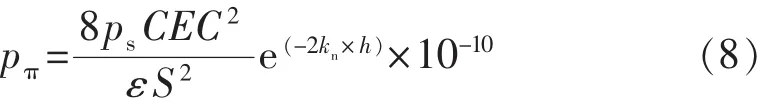
其中

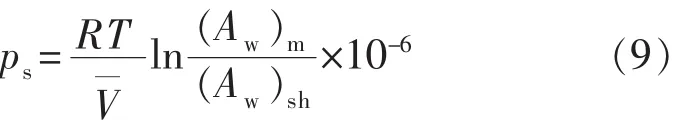
对于氯化钙溶液

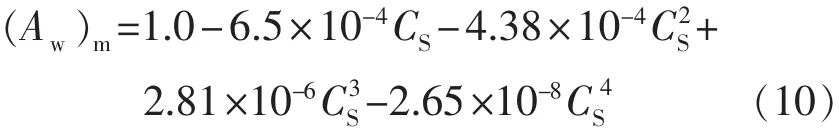
对于氯化钠溶液

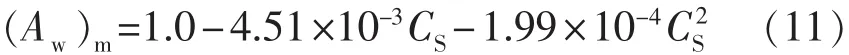
对于氯化钾溶液

式（8）～（12）中：CEC为阳离子交换系数，mEq/100 g；ps为理想透膜的渗透压，MPa；ε为介电常数；S为比表面积，cm2/g；kn为双电层厚度，10-10m-1；h为黏土层间半距，10-10m；CS为孔隙中的平均盐浓度，%。

（4）徐加放等［19］结合实验研究，根据孔隙-线弹性力学基本原理，推导出泥页岩水化应力经验公式。其模型适合于渗透率小于1×10-9D的泥页岩水化应力的微观定量描述，计算公式如下：

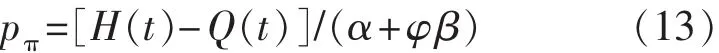
其中

式中：H（t）为实际泥页岩体积膨胀率；Q（t）为t时间的排液体积，cm3/s；k为泥页岩渗透率，D；A为泥页岩横截面积，cm2；Δp为泥页岩两端的压差，Pa；t为水化时间，s；μ为流体黏度，Pa·s；l为岩性长度，cm；α为岩石基质压缩率；φ为泥页岩孔隙度，%；β为流体静态压缩率。

以上4种水化应力计算模型均需要大量的实验数据作为支撑才能计算出水化应力。其中，Marshall和Huang及徐加方等的计算最为直接，Tan等的计算较为复杂。由于徐加放等的计算模型没有考虑储层微裂缝问题，因此计算结果具有一定的偏差性。本次研究中计算水化应力采用的是Marshall和Huang这2种计算模型。

1.3考虑水化应力的破裂压力计算模型

泥页岩地层井壁周围的应力场实际上是力学和化学耦合的结果，国内外学者主要通过2种方法来表征：一种是直接将水化应力作为有效应力的一部分［20］，认为泥页岩水化使得井壁的应力状态发生改变，此方法直观且较简便；另一种是从泥页岩吸水和水化后岩石体积膨胀的关系出发，根据平面应变的弹性力学基本方程，再采用有限元或者有限差分法解出井筒周围的应力状态［21-25］，这种方法在计算上较为复杂，且需要很多的实验数据作为支撑。因此，笔者采用前一种方法来建立考虑水化应力的破裂压力计算模型。

井筒的周向（切向）应力是导致岩石破裂的主要因素，在研究破裂压力时其余应力分量可不做考虑。根据上述思路，将水化应力直接作为有效应力的一部分，并结合公式（5），可得到井壁处的周向有效应力，即

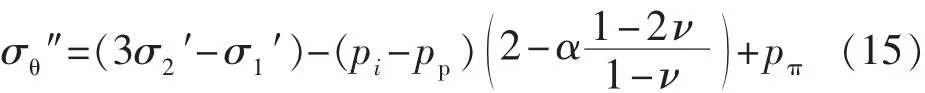
在水力压裂中，破裂压力的计算应用最为广泛的是最大张应力准则，根据这一准则，当井壁岩石的有效周向应力σθ″达到井壁岩石水平方向的最小抗张强度后，岩石将垂直于张应力方向发生破裂，即

由以上可得地层破裂压力pF的表达式为

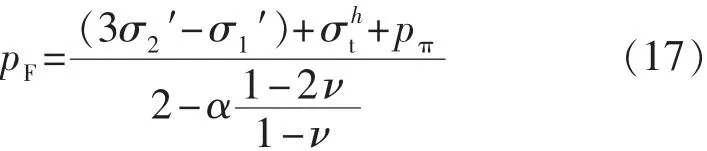
式中：pF为地层破裂压力，MPa；σ1′和σ2′分别为最大和最小水平有效应力，MPa；σt为岩石最小抗张强度，MPa；pπ为水化应力，MPa；α为孔隙弹性常数，无因次；ν为泊松比。

2实例计算

计算所采用的基本参数［26］如表1所列。

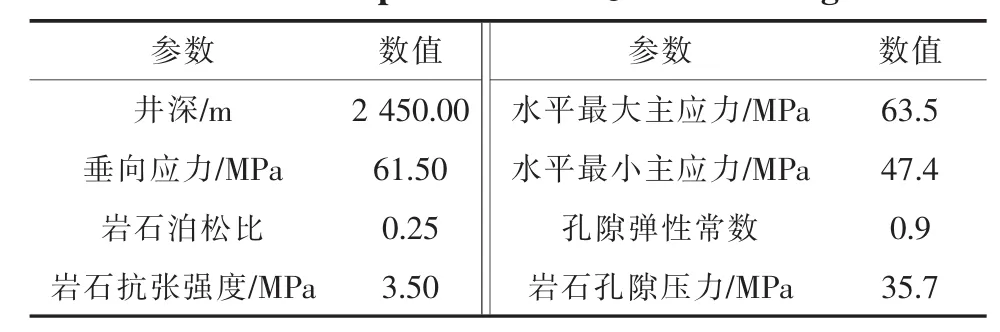
表1　JY1HF页岩气井基本参数Table 1 Thebasic parametersof JY1HF shale gaswell

笔者采用Marshall及Huang模型进行定量计算需要补充的参数如下：

①采用Marshall的计算模型［14-15］。根据文献［15］提供的相关实验数据，其透膜效率为0.1，气体常数为8.314，采用的绝对温度为363 K，纯水偏摩尔体积为1.8×10-5m3·mol-1。由于一般泥页岩地层采用清水或滑溜水进行压裂，则进入地层液体活度可假定为0.78，页岩中水的活度为0.915。

②采用Huang的计算模型。根据文献［18］补充的参数有：阳离子交换系数为20mEq/100 g，比表面积为70m2/g，孔隙中的平均盐浓度为30%，其他相同参数取值同上，其计算结果如表2所列。

表2　地层破裂压力计算结果对比Table 2 Com parison of calculation resultsof fracture pressure

由表2可看出，实际的地层破裂压力为55MPa，不考虑水化应力时所得的破裂压力为53.9MPa，而考虑水化应力后，利用Marshall公式计算出的破裂压力为55.8MPa；采用Huang公式计算出的破裂压力为55.6MPa，比不考虑水化应力的破裂压力计算结果更接近于实际情况。

通过以上计算，表明考虑水化应力泥页岩的破裂压力会增加。这是因为对泥页岩地层进行水力压裂时，钻井液（水基）或压裂液（清水/滑溜水等）进入泥页岩地层使得泥页岩地层发生水化而产生水化应力，造成井筒周围应力的增加，最终导致泥页岩地层的破裂压力增加。

3　结论

（1）笔者建立的新模型为研究泥页岩地层水化应力对破裂压力的影响提供了一种研究思路，但由于没有考虑射孔孔眼以及天然裂缝对水力裂缝的起裂影响，因此本模型只适合于预测裸眼直井情况下的沿岩石本体破裂的压力预测，与实际情况有一定的出入，还需进一步验证，但是笔者提出的新模型的简单计算方法为快速预测页岩储层的破裂压力提供了依据。

（2）笔者采用的2种水化应力计算方法，都只是从理论上对水化应力的破裂压力进行定量分析，而在实际情况下，水化应力可能要比理论计算出的值高很多。因此，在泥页岩储层水力压裂中须要认真考虑这一因素，便于更为准确地预测出储层破裂压力，为施工参数优化提供依据。

（3）目前，对于水化应力的研究需要实验数据来支撑，这为研究水化应力造成了很多困难。因此，需要建立更为全面的模型来研究水化应力，以便能够更好地研究水化应力对泥页岩地层应力的影响，为泥页岩地层钻井、压裂施工等提供可靠的依据。

（References）：

［1］唐颖，唐玄，王广源，等.页岩气开发水力压裂技术综述［J］.地质通报，2011，30（2/3）：393-399. Tang Ying，Tang Xuan，WangGuanyuan，etal.Summaryofhydraulic fracturing technology in shale gas development［J］.Geological Bulletin ofChina，2011，30（2/3）：393-399.

［2］林森虎，邹才能，袁选俊，等.美国致密油开发现状及启示［J］.岩性油气藏，2011，23（4）：25-30. Lin Senhu，Zhou Caineng，Yuan Xuanjun，etal.Status quo of tight oilexploitation in the United Statesand itsimplication［J］.Lithologic Reservoirs，2011，23（4）：25-30.

［3］李传亮，朱苏阳.页岩气其实是自由气［J］.岩性油气藏，2013，25（1）：1-3. Li Chuanliang，Zhu Suyang.Shale gas is free gas underground［J］. Lithologic Reservoirs，2013，25（1）：1-3.

［4］张小龙，张同伟，李艳芳，等.页岩气勘探和开发进展综述［J］.岩性油气藏，2013，25（2）：116-122. ZhangXiaolong，Zhang Tongwei，LiYanghua，etal.Researchadvance inexplorationand developmentofshalegas［J］.Lithologic Reservoirs，2013，25（2）：116-122.

［5］王拓，朱如凯，白斌，等.非常规油气勘探、评价和开发新方法［J］.岩性油气藏，2013，25（6）：35-39. Wang Tuo，Zhu Rukai，BaiBin，etal.Newmethods for theexploration，evaluation and development of unconventional reservoirs［J］.Lithologic Reservoirs，2013，25（6）：35-39.

［6］赵海峰，陈勉，金衍，等.页岩气藏网状裂缝系统的岩石断裂动力学［J］.石油勘探与开发，2012，39（4）：465-470. Zhao Haifeng，Chen Mian，Jin Yan，etal.Rock fracture kinetics of the fracturemesh system in shalegas reservoirs［J］.Petroleum Exploration and Development，2012，39（4）：465-470.

［7］袁俊亮，邓金根，张定宇，等.页岩气储层可压裂性评价技术［J］.石油学报，2013，34（3）：523-527. Yuan Junliang，Deng Jingen，Zhang Dingyu，etal.Fracability evaluation of shale-gas reservoirs［J］.Acta Petrolei Sinica，2013，34（3）：523-527.

［8］路保平，林永学，张传进.水化对泥页岩力学性质影响的实验研究［J］.地质力学学报，1999，5（1）：65-70. Lu Baoping，Lin Yongxue，ZhangChuanjin.Laboratory studyoneffect ofhydration toshalemechanics［J］.JournalofGeomechanics，1999，5（1）：65-70.

［9］张莹莹，黄思静.华庆地区长6油层组方解石胶结物特征［J］.岩性油气藏，2012，24（2）：48-52. Zhang Yingying，Huang Sijing.Characteristics of calcite cements of Chang 6 oil reservoir set in Huaqing area［J］.Lithologic Reservoirs，2012，24（2）：48-52.

［10］和冰.泥页岩地层水化后井眼周围应力的计算模型［J］.钻采工艺，2008，31（增刊1）：11-13. He Bing.A model of calculating the stress distribution near the borehole under hydration［J］.Drilling&Production Technology，2008，31（S1）：11-13.

［11］孙文化，楼一珊，李忠慧，等.水化应力和滤饼质量对地层坍塌压力的影响分析［J］.石油钻探技术，2008，36（1）：28-29. SunWenhua，Lou Yishan，Li Zhonghui，etal.Effectsof hydration stressand filtration cakeon formation collapsingpressure［J］.Petroleum Drilling Techniques，2008，36（1）：28-29.

［12］黄荣樽.水力压裂裂缝的起裂和扩展［J］.石油勘探与开发，1981，8（5）：62-74. HuangRongzun.The fracture initiation and propagation ofhydraulic fracture［J］.Petroleum Exploration and Development，1981，8（5）：62-74.

［13］薛强.弹性力学［M］.北京：北京大学出版社，2006：125-130. Xue Qiang.Elasticity［M］.Beijing：Peking University Press，2006：125-130.

［14］ChenevertM E，PernotV.Controlofshaleswellingpressuresusing inhibitivewater-basemuds［R］.SPE 49263，1998.

［15］Chen Guizhong，ChenevertM E，SharmaMM，etal.A studyofwellborestability in shales including poroelastic，chemical，and thermal effects［J］.Journal of Petroleum Science and Engineering，2003，38：167-176.

［16］Tan CP，RichardsBG，Rahman SS，etal.Effectsofswellingand hydrationalstress in shalesonwellbore stability［R］.SPE 38057，1997.

［17］Tan CP，Rahman SS，Richards BG，etal.Integrated approach to drilling fluid optimisation for efficientshale instabilitymanagement［R］.SPE 48875，1998.

［18］Huang Hong.Numerical simulation and experimental studies of shale interaction with water-base drilling fluid［R］.SPE 47796，1998.

［19］徐加放，邱正松，王瑞和，等.泥页岩水化应力经验公式的推导与计算［J］.石油钻探技术，2003，31（2）：33-35. Xu Jiafang，Qiu Zhengsong，Wang Ruihe，et al.The hydrationstress formula and calculation for deduction of shale formations［J］.Petroleum Drilling Techniques，2003，31（2）：33-35.

［20］刘玉石.地层坍塌压力及井壁稳定对策研究［J］.岩石力学与工程学报，2004，23（14）：2421-2423. Liu Yushi.Collapse pressure and precautions for stability ofwellborewall［J］.Chinese JournalofRock Mechanicsand Engineering，2004，23（14）：2421-2423.

［21］黄荣樽，陈勉，邓金根，等.泥页岩井壁稳定力学与化学的藕合研究［J］.钻井液与完井液，1995，12（3）：15-21. Huang Rongzun，Chen Mian，Deng Jingen，et al.Study on shale stability ofwellbore bymechanics couplingwith chemistrymethod［J］.Driuing Fluid and Completion Fluid，1995，12（3）：15-21.

［22］唐林，罗平亚.泥页岩井壁稳定性的化学与力学耦合研究现状［J］.西南石油学院学报，1997，19（2）：85-88. Tang Lin，Luo Pingya.Research statusof shale stability ofwellbore by chemistry couplingwithmechanicsmethod［J］.Journalof SouthwestPetroleum Institute，1997，19（2）：85-88.

［23］刘平德，张梅，孙明鑫，等.泥页岩井眼稳定的力学及化学耦合方法研究［J］.钻采工艺，2000，23（6）：10-12. Liu Pingde，Zhang Mei，Sun Mingxin，et al.The couplingmethod research on themechanics and chemistry of the shale hole stabilization［J］.Drilling&Production Technology，2000，23（6）：10-12.

［24］邓虎，孟英峰.泥页岩稳定性的化学与力学耦合研究综述［J］.石油勘探与开发，2003，30（1）：109-111. Deng Hu，Meng Yingfeng.A discussion on shalestability coupling withmechanicsand chemistry［J］.Petroleum Exploration and Development，2003，30（1）：109-111.

［25］王炳印，邓金根，宋念友.力学温度和化学耦合作用下泥页岩地层井壁失稳研究［J］.钻采工艺，2006，29（6）：1-4. Wang Bingyin，Deng Jingen，Song Nianyou.Effectsof temperature，chemicaland percolation on wellbore instability in shale［J］.Drilling&Production Technology，2006，29（6）：1-4.

［26］周德华，焦方正，贾长贵，等.JY1HF页岩气水平井大型分段压裂技术［J］.石油钻探技术，2014，42（1）：75-80. Zhou Dehua，Jiao Fangzheng，Jia Changgui，etal.Large-scalemultistage hydraulic fracturing technology for shale gas horizontalwell JY1HF［J］.Petroleum Drilling Techniques，2014，42（1）：75-80.

［27］李传亮，孔祥言.油井压裂过程中岩石破裂压力计算公式的理论研究［J］.石油钻采工艺，2000，22（2）：54-56. LiChuanliang，Kong Xiangyan.A theoreticalstudy on rock breakdown pressure calculation equationsof fracturing process［J］.Oil Drilling&Production Technology，2000，22（2）：54-56.

（本文编辑：杨琦）

Calculationmodelof breakdown pressure in shale formation

YAN Xiangyang1，HU Yongquan2，LINan3，SHEN Beibei4
（1.ENTI，Chengdu 610000，China；2.College ofPetroleum Engineering，SouthwestPetroleum University，Chengdu 610500，China；3.Research Institute of Engineering and Technology，NorthwestOilfield Company，Sinopec，Urmuqi830000，China；4.Research Institute ofEngineering and Technology，HuabeiOilfield Company，Sinopec，Zhengzhou 450000，China）

It is very important to predict formation fracture pressure accurately for successful hydraulic fracturing. Calculating the fracturepressure in shale formation isdifferent from thatin common formationsasa resultofchangesof mechanical properties due to hydration，so the calculationmethod of common formations cannotbe applied tomud shale formation and an in-depth research should bemade on the calculation method of fracture pressure in shale formation.Therefore，based on theoriesofelasticmechanicsand rockmechanics，considering theeffectofhydration on thewellbore stress field，this paper appliedmaximum tensile stress criterion to establish a newmodel for calculating fracturepressureby takinghydration stressintoaccount.Besides，thispaper carried outcalculation examplesby using theestablishedmodelcombinedwith twoways to calculatehydration stressofshale.The resultshows that the fracture pressure in shale formationwith hydration stressconsidered ismuch closer to the fracture pressure in actual formation than thatnot considered.Hence，this calculationmodel provides a reference basis for fast predicting the formation fracturepressure.

shale；fracturepressure；fracturingoperation；hydration stress；hydraulic fracturing；rockmechanics

TE249.6

A

1673-8926（2015）02-0109-05

2014-07-19；

2014-10-25

西南石油大学研究生创新基金项目“页岩地层水力裂缝破裂与延伸机理研究”（编号：GIFSS1118）资助

严向阳（1985-），男，硕士，工程师，主要从事油气田增产理论与改造技术方面的工作。地址：（610000）四川省成都市成华区府青路二段2号。电话：（028）83521801。E-m ail：xycy911@163.com。