简化的DES算法在RFID系统中的应用
苗素贞,彭平
(1.广东技术师范学院,广州 510665;2.广东技术师范学院计算机科学学院,广州 510665)
简化的DES算法在RFID系统中的应用
苗素贞1,彭平2
(1.广东技术师范学院,广州510665;2.广东技术师范学院计算机科学学院,广州510665)
0 引言
无线射频识别(RFID)是一种使用无线通信的方式进行信息识别的技术,由电子标签和识别装置组成,利用它可以对目标对象进行识别并进行相关的数据采集。RFID技术属于自动识别技术中的一种,它也是构成物联网的一项核心技术[1],在20世纪末逐渐进入企业应用领域。RFID技术与其他的技术一样,在它最初被应用的时候人们往往对其充满了想象,并且由于美国国防部和沃尔玛公司的一些举措,人们对该技术在实际中的应用前景充满了期待。然而随着它在不同环境中的应用,人们在对其狂热追捧的同时不得不冷静下来面对RFID应用系统突显出的一系列问题[2]。因RFID系统“对外完全开放”的设计思想,当标签进入阅读器读取范围内时,其信息被读取,阅读器获取物品的信息,甚至是消费者的个人行为如位置、行程、时间等信息。不仅如此,若将RFID技术运用到身份证、工作证等方面,必会招致黑客的入侵,个人的隐私信息将随时面临着暴露的危险性,人们的合法权益将会受到直接影响。由此可见,为了推动RFID技术更好的发展与普及,首先要解决其应用系统的安全与隐私问题[3]。
其实,造成RFID应用系统存在安全风险的原因很多。其中,最主要来源于RFID系统的设计思想,即它的对外应用是完全开放的[4]。其次,该系统的读写机制存在缺陷、标签本身的缺陷以及阅读器与标签之间的通信信道存在不安全性等,这些都会威胁到RFID应用系统的安全。目前,针对该问题的解决方法也有很多,大致上可以分为三大类:物理方法、逻辑方法及两者的结合。主要的物理方法有:Kill命令机制[5]、法拉第网罩[6]、休眠机制、主动干扰[7]和可分离标签[8]等技术,这些方法主要运用于低成本的RFID标签。为了弥补物理方法的不足,很多基于密码学的安全协议和信息加密算法相继被提出。其中,比较有影响性的方法主要有Hash锁协议、随机化Hash锁协议、Hash链协议、基于Hash的ID变化协议、LCAP协议等,经过分析,这些协议虽然可以在特定的应该场景下解决部分的安全与隐私问题,但遗憾的是它们往往在解决某一问题的同时,又会带来新的问题。总的来看,目前尚不存在一个公认的高效、实用、低成本、适用于RFID环境的安全的解决方案,这也为后续的进一步研究与改进提供了发展空间。
1 混沌加密技术及RFID信息加密系统

混沌加密是利用确定的混沌系统经过多次迭代之后生成的混沌序列作为密钥序列,利用该序列对明文信息进行加密,密文经信道传输,接收方收到密文后用混沌同步的方法进行解密得到明文的一个过程。其原理可以通过图1来表示:其中,P表示明文,C表示密文;F(K0)表示混沌系统的初始状态,即动力学方程的初始值及其参数;∑(KE)和∑(KD)分别表示用于加密和解密的密钥生成器;E(P,KE)和D(C,KD)分别表示加密和解密的过程。

图1
在图1中,P表示明文,C表示密文;F(K0)表示混沌系统的初始状态,即动力学方程的初始值及其参数;∑(KE)和∑(KD)分别表示用于加密和解密的密钥生成器;E(P,KE)和D(C,KD)分别表示加密和解密的过程。在进行安全通信之前,首先需要设定混沌系统的初始状态,即动力学方程的参数及其初始值,这些数据经过RSA加密算法加密之后在通信双方之间进行安全传递。因混沌系统产生的序列具有随机性,保证了每次用于加密的密钥KE是不相同的,并且该序列具有不可预测性,因此,本文中选择的是混沌加密算法。

事实上,并不存在绝对安全的密码系统,在通常情况下我们认为下面几种情况的加密系统是安全的:如果攻击者破译一个加密算法所需的费用远远超过被加密信息本身的价值,或者破译时所需要的时间过长超过信息本身的保密期,或者破译时需要大量的数据超过了信息本身的数量,则认为该加密算法是安全的。
在进行加密系统设计时,一般需要考虑以下几个问题:
(1)一个好的加密系统其安全性应该只和加密密钥相关,即使攻击者获取了加密算法的细节,加密系统应具备的保密程度也不会降低。
(2)密钥量应该足够大,以满足“一次一密”的保密要求和所需的保密等级。
(3)算法中不应该存在“弱密钥”,即所用密钥的保密程度应该是相同的。
(4)加密算法应具备抵御已知明文攻击的能力,即使攻击者获取了一部分的明文及其相应的密文,也无法实现数据其他部分的解密,更不可能破解密钥。
除此之外,针对RFID应用系统而言,还需考虑到电子标签的运算能力、存储空间、加密的硬件成本等问题,在进行加密系统设计时尽量做到以下几点:
(1)选用的算法的加密方式尽量是较为简单,因RFID应用系统中电子标签的容量非常有限,若选用复杂的算法,加密时就需要付出巨大的代价。另外,从实时性方面考虑,进行算法设计时尽量选用可并行处理的算法。
(2)考虑要RFID应用系统中电子标签的硬件成本,本文中选择在标签的芯片内只加入加密模块,而在阅读器的控制处理模块中可以加入加密与解密的模块,从而来实现操作和提高速度。

为了获取更大的混沌空间以及对初始状态更高的敏感性,本文在Logistic映射的基础上对其进行改进,改进的Logistic映射表达式为:
f(x)=μx(1-x2)(1)
我们取x0=0.2,讨论μ的取值情况:
当0<μ≤1时,(μ=0.3时,如图2(a)所示)该模型所决定的离散动力系统的动力学形态十分简单,曲线迅速趋于0,且x0=0为吸引不动点,0就是吸引子。除了不动点之外,再也没有其他的周期点。
当1<μ<2时,(μ=1.8时,如图2(b)所示)系统的动力学形态也较简单。
当2≤μ≤3时,(μ=2.4,μ=2.99时,如图2(c)、(d)所示)系统的动力学形态十分复杂,系统由倍周期通向混沌。
当μ>3时,此时该系统状态毫无混沌现象,0为唯一的吸引子。
经过MATLAB仿真实验发现,当2.3<μ≤3.0时,该模型出现混沌状态。取参数μ=3.0时,改进的Logistic映射的吸引子图如图3所示;当参数x0=0.2时,其倍周期分岔图如图4所示。
为了验证其是否具备初始条件敏感性,我们取x0=0.32560和x0=0.32561进行测试,改进后的Logistic映射轨道间的指数分离现象如图5所示,由此可以说明,改进后的Logistic映射具备对初始条件极端敏感的特性。同时,我们可以发现,改进后的Logistic映射的混沌区间为(2.3,3.0),明显大于改进前的混沌区间(3.57,4.0),也就是说改进后的Logistic映射能够产生密钥的空间更大了,可以为后期的加密算法提供更多的密钥。

图2 时间序列图

图3 改进的Logistic的吸引子图

图4 改进的Logistic映射的分岔图

图5 轨道的指数分离图
2 简化的DES加密算法
商用数据加密标准DES算法是由美国国家标准局颁布的,该算法执行速度较快,适用于大量数据的加密,并且加密之后的数据具有很好的雪崩效应。但是DES算法每加密一组数据要进行16轮的循环加密,且16轮的密钥之间存在相关性,基于这些原因,本文选择在DES加密算法的基础上提出一种简化算法用于RFID应用系统中,从而对RFID用户的安全与隐私起到一定的保护作用。

DES是一个分组密码算法,属于私钥加密体制,其密钥长度为56位,但是用64位表示,有8位为校验位。该算法首先对明文进行分组,每组明文的长度为64位,之后分别对每个分组进行加密。但是直接用DES算法对RFID系统的数据进行加密会存在以下问题:
(1)利用该算法时,每组明文需要进行16轮的加密,导致加密速度较慢,占用存储空间大。
(2)每轮的轮密钥均是由初始密钥先置换后移位的方式获取,因此子密钥与初始密钥之间存在线性相关性。并且初始密钥固定不变,那么轮密钥也不会发生变化。如果要增强该算法的抗破译性,就需定期地更换DES算法的初始密钥,这样会造成加密端和解密端初始密钥不同步的问题。
针对以上问题,本文在DES算法的基础上对其做以下简化:
(1)减少加密轮数,由原来的16轮降低为4轮;相应的,轮密钥直接由Logistic映射生成48位的轮密钥,这样可以大幅度地降低加密算法的复杂度。
DES采用的结构通常称为Feistel系统,1988年Michael Luby和Charles Rackoff分析了该结构,证明如果轮函数是以密钥Ki为种子的安全伪随机函数,则进行三轮足以使分组加密后数据是伪随机排列,进行四轮足以使得加密后数据成为“强”伪随机排列[9]。因此本文将DES算法中的16轮循环加密简化为4轮。
(2)由混沌映射作为轮密钥发生器,确保轮密钥处于变化之中且相互独立,实现了“一次一密”,提高了加密算法的安全性。并且运用混沌加密技术时,只要在互相通信的两端分别构造混沌映射,在初始状态相同的情况下,就可保证通信双方能够生成相同的混沌序列,实现密钥的同步。

图6 简化的DES算法加密过程示意图

图7 简化的DES的f函数

简化后的加密算法过程如图6所示,主要涉及三个步骤:
(1)明文P经过初始置换,得到P0=IP(P)。记作P0= L0R0,其中L0是P0的前32位,R0是P0的后32位。
(2)对1≤i≤4,执行以下操作:Li=Ri-1;Ri=Li-1⊕f(Ri-1,Ki),其中Ki是由混沌映射迭代产生的混沌序列经量化后得到的。Ki是加密算法的轮密钥,是一个48位的串,Ki相互之间是独立的。f是一个函数,如图7所示。
(3)左右交换,得到R4L4,用初始置换的逆作用得到密文C=IP-1(R4L4)。解密过程完全一样,只是密钥K1,K2,…,K4的次序颠倒。在加密过程中的第三步有一个左右交换,这样在解密时就没有必要再做左右交换。其解密过程如下:
①输入密文C(即RnLn),输出[Ln][Rn⊕f(Ln,Kn)]。从加密过程得知Ln=Rn-1,Rn=Ln-1⊕f(Rn-1,Kn),因[Ln][Rn⊕f(Ln,Kn)]=[Rn-1][Ln-1⊕f(Rn-1,Kn)]=Rn-1Ln-1。
②同理,第二步解密将Rn-1Ln-1变为Rn-2Ln-2。继续下去,解密过程最后得到L0R0。

改进的Logistic映射的离散模型为:
f(x)=μx(1-x2)
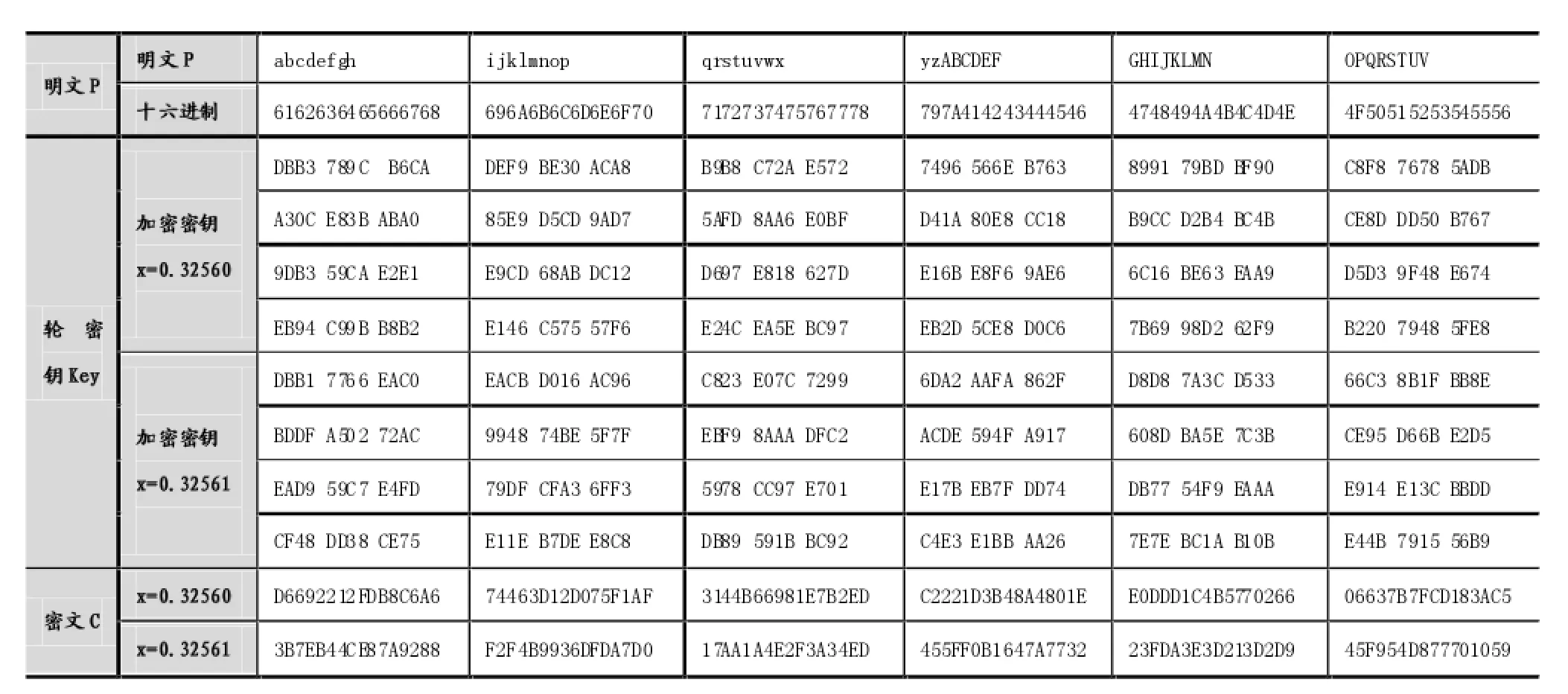
其中,1<μ≤3,-1 为了获取加密算法的轮密钥,需要对混沌序列进行二进制编码,本文中采用的映射函数为gk,其定义为:gk(x)=x×2k,x∈(-1,1),其中k为二进制编码长度。因受到计算机精度的限制以及混沌映射的倍周期规律,本文中取混沌映射的初始迭代次数n=1000,二进制编码长度k=16。将3个连续的混沌序列项进行处理,得到一个轮密钥Ki,即Ki={g16(x1)g16(x2)g16(x3)}。 在本文中利用MATLAB进行仿真实验,包括两个部分:第一部分主要是进行加密算法初始值敏感性的测试,给定两个仅仅相差10-5的初始值进行MATLAB仿真,比较生成的密文信息;第二部分主要是对于给定的明文字段分别利用DES算法和简化后的DES算法进行加密处理。 本文中选定的明文字段P为:abcdefgh ijklmnop qrstuvwx yzABCDEF GHIJKLMN OPQRSTUV,其对应的十六进制形式为:6162636465666768 696A6B6C6 D6E6F70 7172737475767778 797A414243444546 4748 494A4B4C4D4E 4F50515253545556。 实例1:利用简化算法对明文字段进行加密,分别给定两个不同的初始值对明文进行加密,其结果如表1所示。 其中两次仿真的初始值分别为x0=0.32560和x0= 0.32561值,在表1中可以看出因初始值不同,用于加密的轮密钥发生很大的变化,从而使两次仿真得到的密文完全不同,这也很好地验证了简化后的DES算法具有很好的抗破译性。 实例2:利用简化算法和原算法对同一明文字段进行加密,其加密结果如表2所示:其中,原算法的初始密钥为:“D17A530F930A4B2E”,其轮密钥是通过对初始密钥进行置换与移位获得的。 从加密所占用的时间来看,简化后的算法由于每组明文循环加密的轮数降低,且轮密钥不再需要通过置换与移位操作获得,因此,对于同一段明文信息,其加密时所需的时间相对较短,约为原算法所需时间的52%。从占用的存储空间来看,DES算法加密轮数和移位计算次数较多,占用的内存和外存储空间较多;简化后加密的轮数降低,轮密钥不再通过循环移位获取,占用的存储空间相对较少。因此,简化后的算法比较具有优势。 在信息加密领域,目前经常使用的攻击方法主要有明文攻击、差分攻击、统计攻击以及其他各种恶意攻击。在本文中主要通过进行密钥敏感性分析、统计分析和差分分析来检验加密算法的安全性。 一个好的加密算法其安全性应该只和密钥相关,即使攻击者知道了算法的细节,也不能降低算法的保密程度。同时,加密算法应该能够提供足够多的密钥,这样才能保障加密算法能够抵抗穷举攻击。 (1)密钥敏感性测试 通过图5和表1可以看出,该算法对初始状态十分敏感。该算法属于对称加密体制,解密过程为加密的逆过程,解密时若初始值发生微小的改变,解密得到的信息将会发生很大的改变,在该算法中初始值是通过安全性极高的RSA算法加密,攻击者很难破获其初始值。因此,即使非法分子截获了部分的信息,也很难将其进行正确的解密得到明文信息。 表1 简化后的DES加密效果图 表2 简化后的DES加密效果图 (2)密钥空间分析 在该算法中,混沌映射参数μ可取(2.3,3.0)之间的任意实数,初始值可以取(-1,1)之间的任意实数,仅参数μ的选取就具有无穷性。因此,该加密算法拥有足够大的密钥空间,利用穷举法获取加密系统的初始状态是不可能的。 简化后的算法,其轮密钥是由混沌映射产生的混沌序列进行二值化处理得到的,具有随机性,且相互之间彼此独立。因此,加密系统可实现“一次一密”,具有较强的抗统计分析能力。 差分攻击是一种明文攻击方式,主要是通过对一定的明文信息进行微小的改变,分析该变化对密文造成的影响来获取密钥的相关信息。简化后的算法只要对明文信息进行微小的改变,加密得到的密文信息将会发生巨大的改变,攻击者通过这种方式得到的结果是没有任何意义的。 通过以上分析可以看出本文提出的简化算法在理论上是可行的,并且能够实现。由于混沌系统对初值的极端敏感性,只有通信双方的混沌映射函数、函数的初始状态完全一致的情况下,才能正确地解密。如果不能获取这些信息,要想破解出明文信息是非常困难的。 本文在分析了RFID存在的安全与隐私问题之后,针对RFID应用系统的特点将混沌加密技术应用到加密系统中。主要针对典型的混沌映射Logistic映射进行改进,并将其作为加密算法的轮密钥生成器;在对称加密算法DES的基础上提出一种简化算法,经MATLAB仿真验证简化后的DES算法在一定程度上提高了系统的安全性,适合RFID应用系统。 [1]胡向东,魏琴芳,向敏等.物联网安全[M].北京:科学出版社,2012:313. [2]黄玉兰.基于物联网的RFID电子标签研究进展[J].电讯技术,2013,53(4):522-529. [3]黄玉兰.基于物联网的RFID电子标签研究进展[J].电讯技术,2013,53(4):522-529. [4]李仲阳,刘金平,李婷婷.RFID系统安全性研究[J].计算机安全,2011,2:36-38. [5]Auto-ID Center.860MHz-960MHz class I radio frequency identification tag radio frequency&logical communication Interface specification proposed recommendation Version 1.0.0[R].Technical Report MIT-AUTOID-TR-007.Nov.2002. [6]A.Juels,R.L.Rivest,M.Szydlo.The blocker tag:selective blocking of RFID tags for consumer privacy[C].Proceedings of the 10th ACM Conference on Computer and Communication Security(CCS 2003).Washington DC,USA,2003:103-111. [7]T.Hjorth.Supporting privacy in RFID systems[D].Technical University of Denmark,Master thesis.2004. [8]胡向东,魏琴芳,向敏等.物联网安全[M].北京:科学出版社,2012:325. [9]Michael L,Charles R.How to construct pseudorandom permutations from pseudo random functions[J].SIAM Journal on Computing,1988,17(2):373-386. RFID System;Chaotic Sequence;Logistic Map;DES Application of Simplified DES Algorithm in RFID System MIAO Su-zhen,PENG Ping 1007-1423(2015)19-0003-07 10.3969/j.issn.1007-1423.2015.19.001 2015-05-20 2015-06-25 目前,无线射频识别技术被广泛地应用到很多领域,但随着RFID标签应用到单品级消费品中,RFID系统突显出一些安全与隐私问题。主要针对Logistic映射进行改进,将它作为加密算法的轮密钥发生器,并在DES算法的基础上提出一种简化算法,并利用MATLAB进行仿真实验。验证提出的简化算法在理论上具备一定的安全性和抗破译性,更适合RFID应用系统。 RFID系统;混沌序列;Logistic映射;DES 苗素贞(1987-),河南驻马店人,研究生,研究方向为信息系统工程 彭平(1956-),教授,研究方向为智能信息处理、智能学习系统 At present,Radio Frequency Identification technology has been widely applied to many fields,but with the electronic tags applied to a single grade in consumer products,the system of RFID highlights a number of the security and privacy issues.Focuses on the Logistic map and tries to improve it as a chaos sequence generator.Proposes a simplified algorithm based on DES algorithm and carries out the simulation with MATLAB software to further verify that the simplified DES algorithm has a certain security and anti-attack in theory.It is more suitable for RFID application systems.
3 加密算法的安全性能分析



4 结语
(1.Guangdong Polytechnic Normal University,Guangzhou 510665;2.School of Computer Science,Guangdong Polytechnic Normal University,Guangzhou 510665)

