基于最优格拉斯曼序列的多用户检测*

陆家明，汪立新，2，祁 浩

0 引言

在CDMA系统中，常见的CDMA扩频码本能够容纳的用户数一般都不超过扩频码的长度，如m序列、Gold序列。当频带资源受限，激活用户数超过扩频码本长度时，称该CDMA系统处于“过载”状态，相应地就必须考虑能够容纳更多用户数的码本［1］。WBE(Welch Bound Equality)序列是指总平方互相关达到最低的序列，能够用来组建“过载”状态下CDMA系统的扩频码本［2－3］。最优格拉斯曼序列又被称为MWBE(Maximum Welch Bound E-quality)序列，是一种特殊的WBE序列。相比于一般的WBE序列，最优格拉斯曼序列具有更稳定的结构，所有元素间均具有相同的互相关，更适合用来作为CDMA的扩频码本［4－5］。然而，当系统“过载”时，用户间的干扰就会变的非常大，虽然最优格拉斯曼序列是所有相同大小的码本中，序列间最不相关的码本，但是采用已有的多用户检测方法还是会有较大的误码率。本文借鉴了文献［6］中对于二值优化问题的处理方法，提出了一种基于最优格拉斯曼序列的多用户检测预处理的方法，使得系统的误码率得到进一步的降低，并且能够同时减少后续多用户检测的运算量。

1 CDMA信道模型

考虑某一同步CDMA系统，总共有N个用户，扩频增益为m，即每个用户都用一个长度为m的序列进行扩频，令 sk表示第k个用户的扩频码，且‖sk‖ =1，k=1，2，…，N，其中，‖·‖为 l2范数。定义矩阵 S= [s1，s2，…，sN]。在一个符号周期内，到达接收机的信号可以用下式来表示:

式中，Ak表示第k个用户的信号到达幅度，bk表示第k个用户发送的信息，n表示高斯白噪声。经过匹配滤波器后，信号可以表示为:

式中，A=diag{ A1，A2，…，AN}，R为码本的互相关矩阵。

最优多用户检测［7］是用穷举的方法挑选出最可能的比特序列，又被称为最大似然序列检测(Maximum Likelihood Sequences Detection，MLSD)。最优多用户检测可用如下式子表示:

式中，H=ARA。最优多用户检测理论上可以通过最优多用户检测方法使系统达到最低的误码率，但是由于过于复杂的计算，最优多用户检测很难在实际中得到应用［8］。

2 二值优化问题

首先给出形如下式的二值优化问题:

式中，B是一个N×N的对称矩阵，其非对角线元素相对于对角线元素拥有较小的值。对于式(4)中的矩阵B可以作如下分解:

式中，Bd是由B中的对角线元素组成的对角矩阵，B+和B－分别保留了B中所有正的和负的非对角元素，其余值取0。设中，xi，xj∈{0，1}，1≤i，j≤N则对于任一i，Q(x)可以分解为:

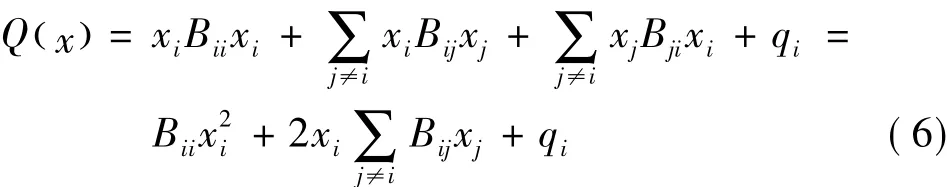
式中，qi表示与xi无关的项。由于xi只能取0或者1，因此xi满足xi=x2i，则上式可进一步简化为

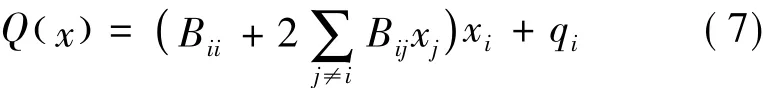
假设除xi外，其他值均已得到最优判决，pi的值便可以确定，则

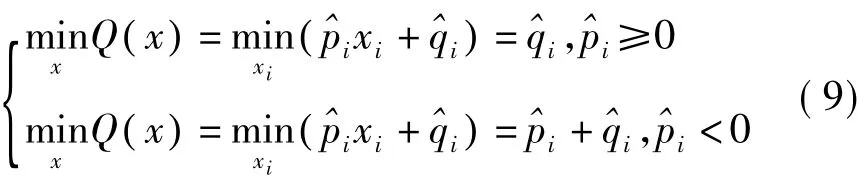
根据上式的取值条件，对应地可以得到

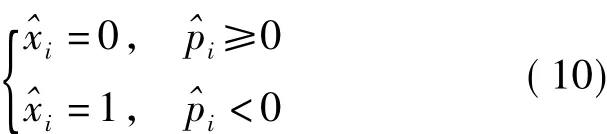
则

而对于¯pi，根据式(5)有

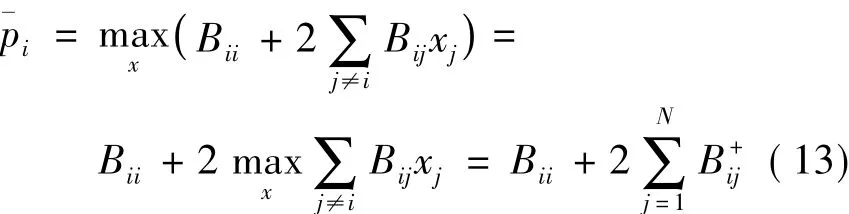
式(13)的最后一步是基于这样一个简单的推断:由于 xj只能取 0 和 1，则当 Bij＞0 时，xj取 1，当 Bij＜0时，xj取0，能使求和部分够取得最大值。同理，有

这样式(12)便可以写成如下形式:

而对于式(4)，最优判决表达式可以写成如下的形式:

3 多用户检测预处理方法

为了将上一节的方法运用到多用户检测中，可将最优多用户检测的表达式(3)稍作修改，写成如下形式:

设^b=2¯b－e，其中e为所有元素均为1的列向量，这样，¯b中的0，{}1分别对应于^b中的－1，{}1。则式(17)可以转化为:

式(18)最后一步中省略了常数项。采用最优格拉斯曼序列作为扩频码本时，根据框架理论中最优格拉斯曼框架的概念可知，码本的互相关达到了最低，而且任意两个用户间的互相关是相等的。因此，最优格拉斯曼序列的互相关矩阵中有较小的非对角线元素，此时的H满足式(4)中B的条件。这样，最优多用户检测便转化为式(4)的形式，而式(16)的判决条件可以转化为:

根据式(19)便可对接收信号进行多用户检测前的预处理，对某些符合上述判决条件的用户信号进行提前判决，且该判决是最优的。随后，从总接收信号中去掉这些已经得到判决的用户的信号。对于剩余的无法最优判决的用户信号，可通过前面提到的多用户检测方法进行检测。由于预处理后的接收信号中已经去掉了最优判决的用户信号，后续的多用户检测所需检测的用户数得到了降低，而且同时减小了剩余信号中的用户间干扰，使得再用多用户检测技术解调时变得更加简单，系统的误码率性能得到了改善。根据式(4)中对矩阵B的要求可知，在多用户检测中使用上述预处理方法时，要求系统所使用的码本具有较低的互相关度。

当系统采用最优格拉斯曼序列作为扩频码本时，根据框架理论中最优格拉斯曼框架［9］的概念可知，码本的互相关达到了最低，而且任意两个用户间的互相关是相等的。因此，最优格拉斯曼序列的互相关矩阵中有较小的非对角线元素，且这些元素的绝对值均相等，满足上述预处理方法的要求。设最优格拉斯曼序列中任意两个用户的互相关为ρ，则:

使用最优格拉斯曼序列时，若有良好的功率控制，所有用户信号的到达功率均为A，则上述式(19)的判决条件可进一步简化为:

式中，¯N表示系统中的激活用户数。

图1为使用上述预处理方法的解相关［10］多用户检测和单纯的解相关多用户检测时，系统中所有用户的平均误码率仿真结果，其中，系统均采用10，()16最优格拉斯曼序列作为用户的扩频码本，激活用户数为11，即系统处于“过载”状态，并假设系统处于高斯白噪声环境，且具有理想的功率控制。从图中可以看出，使用预处理方法后，系统的误码率得到了改善。而图2为信噪比固定为8 dB，激活用户数从2逐渐增加到16的过程中，使用预处理方法和不使用预处理方法的解相关多用户检测误码率。从图中可以看出，在各种用户数条件下，使用预处理方法的多用户检测技术均具有较明显的优势，尤其是在用户数较多，用户间干扰较大时。而且该预处理方法属于简单的硬判决，本身的计算量较低，判决之后，剩余信号中的用户数和用户间干扰均得到了降低，在一定程度上也为后续的多用户检测减少了运算量。

图1 使用预处理方法和不使用预处理方法的解相关多用户检测误码率

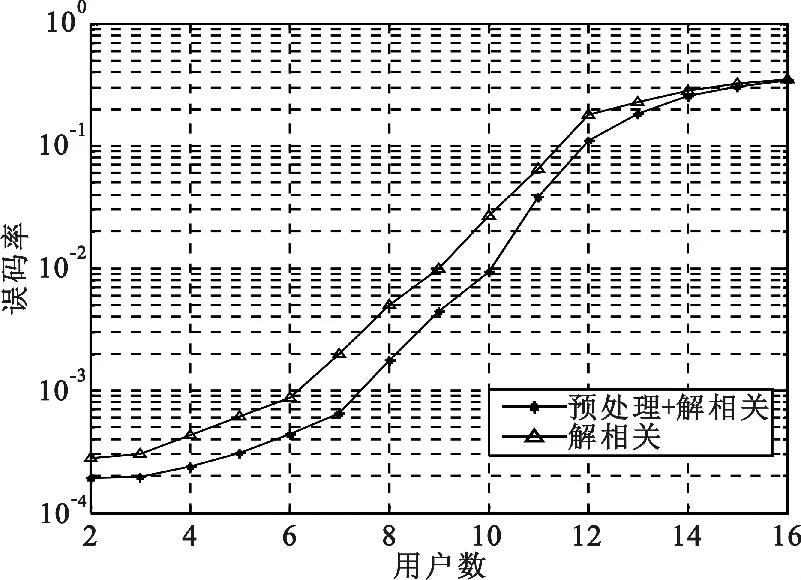
图2 不同激活用户数情况下使用预处理方法的解相关多用户检测误码率

4 结语

针对CDMA系统“过载”状态下用户间干扰过高的问题，本文提出了一种基于最优格拉斯曼序列的多用户检测预处理方法。相较于普通的多用户检测技术，采用最优格拉斯曼序列作为扩频码本，使系统能够达到更低的误码率，同时能降低对多用户检测的运算量。但是，当激活用户数较多时，系统还是有较高的误码率。最优格拉斯曼序列具有非常好的结构特点，如何充分利用最优格拉斯曼序列的特性，进一步降低误码率从而扩大系统容量依然值得深入研究。

［1］ Kumar P，Chakrabarti S．BER Analysis of Hard Decision Interference Cancellation Receiver for Overloaded DSCDMA System［C］//Sarnoff Symposium．Princeton，NJ:IEEE，2008(4):1－5．

［2］ Sarwate D V．Meeting the Welch Bound with Equality［M］．Sequences and Their Applications．Springer London，1999:79－102．

［3］ HU Hong－gang，WU Jin－song．New Constructions of Codebooks Nearly Meeting the Welch Bound with Equality［J］．IEEE Transactions on Information Theory，2014，60(2):1348－1355．

［4］ Heath R W，Strohmer T，Paulraj A J．Grassmannian Signatures for CDMA Systems［C］//Global Telecommunications Conference，San Francisco，USA:IEEE，2003:1553－1557．

［5］ Heath R W，Strohmer T，Paulraj A J．On Quasi－Orthogonal Signature for CDMA Systems［J］．IEEE Transactions on Information Theory，2006，53(3):1217 －1226．

［6］ Axehill D，Hansson A．A Preprocessing Algorithm for MIQP Solvers with Applications to MPC ［C］//43rd IEEE Conference Decision Control，Atlantis，Paradise Island，Bahamas:IEEE，2004:2497－2502．

［7］ Rose C，Ulukus S，Yates R D．Interference Avoidance for Wireless System［C］//Vehicular Technology Conference Proceedings，Tokyo:IEEE，2000:901－906．

［8］ 方雷，梁晓雯．基于球形译码的联合多用户检测［J］．通信技术，2011，44(09):56 －58．FANG Lei，LIANG Xiao － wen．Joint Multi－ user Detectors based on Sphere Decoding in MIMO Multi－Carrier System［J］．Communications Technology，2011，09:56 －58．

［9］ 江宁馨，李峰．多用户检测中解相关检测和最小均方误差检测的研究［J］．计算技术与自动化，2010，29(04):7－10．JIANG Ning－ xin，LI Feng．The Study of Decorrelation Detection and MMSE Detection in Multi－user Detection［J］．Computing Technology and Automation，2010，29(04):7－10．

［10］ Strohmer T，Heath R W．Grassmannian Frames with Applications to Coding and Communication［J］．Applied and Computational Harmonic Analysis，2003，14(3):257－275．