最大化能量效率的协作频谱感知优化算法*

唐菁敏，曹操，张晓颍，马社方

0 引言

近年来的研究表明，认知无线电的大部分的授权频谱没有得到充分有效的利用，但是频谱资源却非常的短缺［1］。美国联邦通信委员会(Federal Communications Commission，FCC)对此现象作了深入的研究，发现实际授权频段的利用率仅15% ～85%［2］。为了解决这个问题，并满足现代日益发展的通信需求，使已分配的授权频谱得到更充分的利用，认知无线电这一重要技术应运而生。频谱共享是认知无线电最基本的思想，它通过检测授权信道的空洞后在对现有授权用户只造成微小限制干扰前提下有效地利用频谱空洞利用空闲的信道进行通信。但是，由于实际通信情况下会有多径衰落以及阴影效应等因素的存在，单个认知用户的检测性能以及可靠性已经满足不了实际的要求了。因此越来越多的采用多个认知用户合作参与频谱感知的方法来进行协作频谱通信。尽管认知无线电协作频谱感知的方法提高了认知无线电的整体性能以及降低多路径衰落和阴影，然而，大量用户的协作频谱感知却增加了系统的能耗，以及协作过程中感知结果的交换浪费了宝贵的时间，还导致了系统的延迟和降低了系统的性能［3-4］。文献［5］提出了一种仅用于优化感知用户数量的最优量化器的方法。文献［6］提出了一种信任投票的方案，每个用户只有在给定的置信标准下才发送其感测结果，而置信标准是从本地的历史结果与最终结果相比计算出来的。文献［7］提出了只有有用的测试统计数据才能被传输到融合中心的方法，但是在这种方法之下，所有的感知用户仍然在时刻进行频谱感知，消耗了大量的能量。文献［8］提出了一种用于优化决策的方法被以便最大化能源效率。文献［9］提出了一种基于集群的频谱感知方法，让每个组用户选择簇头，以处理他们的感知结果，然后上报一个代表所有的感知用户的最终决策。但是，在这种情况下，所有的用户仍感测的频谱。此外，由于簇头和集群成员之间的信息交换，额外的能量仍被消耗。从这些方面考虑，它遵循了减少感知的用户数的做法，因为它降低了感知能量和传送感知结果所消耗的能量，基于文献［10-12］所提的此种方案考虑，本文在一个有限的时间资源内，分析协作频谱感知过程对系统的能量消耗和吞吐量的影响，提出了一种基于最大能量效率的协作频谱感知优化算法。通过优化感知用户的数量来降低能量消耗和最大化系统的吞吐量，进而达到最大化系统的能量利用效率的目的。

1 系统模型

假设一个认知无线网络有NT个认知用户，认知用户必须在不干扰授权用户的前提下进行数据的传输，因此，认知用户须进行频谱感知检测未使用的授权频谱，以便能够进行数据传输，文中我们用最简单并且最有效的频谱检测技术:能量检测［13］。运用能量检测技术，用户检测的基本模型被假设为是二元假设检验问题:

式中，n(t)是随机变量t服从均值为0，方差为σ2n的高斯白噪声信号，x(t)是服从方差为σ2x的高斯分布的主要用户的信号。

在频谱感知之后，所有的感知结果都被传送到融合中心，融合中心将对所有的结果进行加权融合得出最终判决结果［14］，这个协作频谱感知的过程是非常有用的，它减轻了多路径衰落和阴影的影响。在每个认知用户发送的能量样本传送到融合中心后，融合中心将把这些接收到的数据的平均值与预设的阈值进行比较，并作如下决策:

式中，D表示决策结果，A表示数据的平均值，λ表示预设的阈值。

1． 1 频谱感知精确度

有两个非常重要的指标来评估协作频谱感知的性能:探测概率PD和虚警概率PF。探测概率表示在授权用户出现时认知用户探测到授权用户出现时的概率，探测概率的值偏低代表认知用户对首要用户的干扰大;虚警概率表示在授权用户未出现时系统误判其出现了的概率，虚警概率的值高表示系统对频谱的利用率低。本地判决门限的选取对二者的值的高低也有很大的影响。假如判决门限设置的过低，则虚警概率相应的上升。PD和PF的表达式如下［15］:

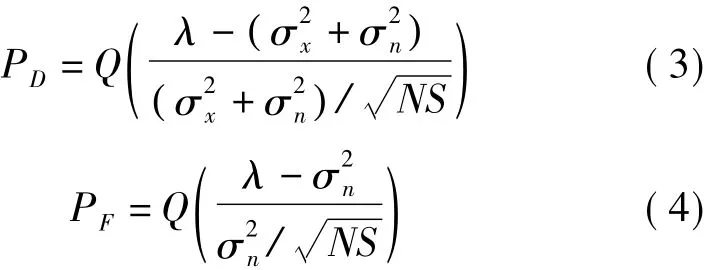
在这里，假设一个探测概率为PthD以满足给定的阈值 λ，其表达式为［16］:

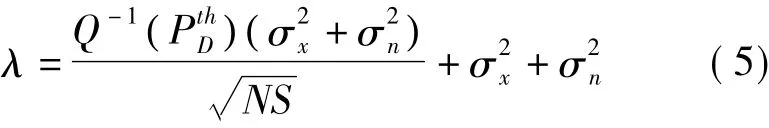
将式(5)代入式(4)可得出:

1． 2 合作频谱感知帧结构

协作频谱感知的时间资源的利用分为3个过程:频谱感知过程、传送感知结果的过程、主要数据传输过程。其帧结构如图1所示。这里假设一帧的总时间为T，频谱感知时间为Ts，传送感知结果时间为Tr，主要数据传输时间为Tt。可得出T=Tt+Ts+Tr。假设一般情况下，数据传输时间Tt是固定不变的，Ts和Tr在不同的系统里是变化的。这里把每个认知用户传送感知结果见融合中心的时间设为τ，则 Tr=Nτ，在每一帧里有(见图1):

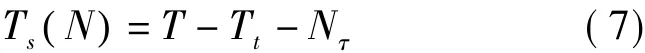
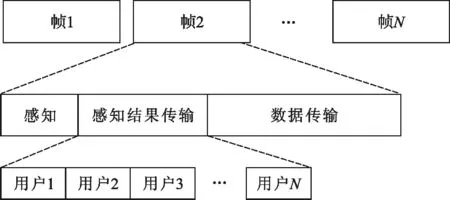
图1 合作频谱感知帧结构

1． 3 频谱感知过程中的最小能量消耗

在频谱的感知过程中，能量的消耗主要有3个部分:频谱感知过程消耗的能量Es、传送感知结果的过程消耗的能量Er、主要数据传输过程消耗的能量Et。在协作频谱感知过程中，只有当频谱被判定为空闲时才能被认知用户利用，在频谱感知信道为空闲时的频谱空闲概率Pf为:

式中，P0是频谱实际为空闲的概率，P1是频谱实际为被占用的概率，P0+P1=1，又因为 PD=PthD，所以有:

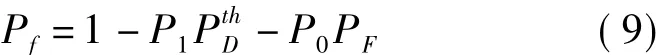
因此，以N个认知用户为变量的系统能量消耗表达式为:

式中，Es()N为频谱感知过程消耗的能量，Er( )N为传送感知结果的过程消耗的能量，Et为主要数据传输过程消耗的能量。

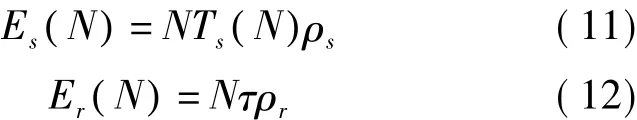
式中，ρs为每个认知用户频谱感知过程消耗的能量，ρt为每个认知用户主要数据传输过程消耗的能量。ρr为每个认知用户传送感知结果的过程消耗的能量。

因为不同数量的认知用户会引起频谱感知和传送感知结果的时间的不同，必然会导致能量消耗的改变，因此存在一个最优的感知用户数量可以将系统的能量消耗降到最低。优化如下:

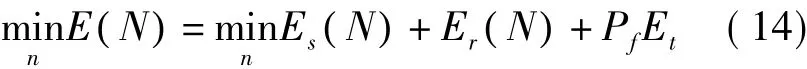
将式(8)～式(13)代入式(14)，可以将E(N)表达为:

可得出Et是N∈［1，NT］的一个凹函数，使能量消耗达到最小的认知用户的数量可表达为:

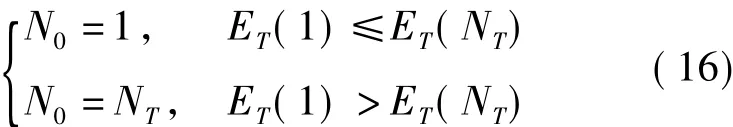
式中，ET(1)和ET是相应个数的认知用户参与

1． 4 系统的吞吐量

系统的吞吐量与参与协作频谱感知用户的数量密切相关。当参与协作频谱感知的用户数量N非常大时，虽然系统的探测概率增高，虚警概率降低，但是系统的感知时间和能量消耗也增大了，这也相应的降低了认知系统的吞吐量，当参与感知的用户数量N非常小时，系统的探测概率降低，虚警概率增高，此时的误差非常大，也不利于系统性能的稳定。因此，优化参与协作频谱感知的用户数量N对系统的吞吐量的影响非常大。下面给出了优化参与协作频谱感知的用户数量N的算法，定义的系统的吞吐量函数如下:频谱感知消耗的能量。因此有:

式中，R0表示认知用户检测到授权用户时的吞吐量(此时授权用户未出现)。

式中，C0为授权用户未出现时的系统的吞吐量C0=lb( 1 +SNRs)，信噪比为代表认知用户接收到的信号的功率，N0代表噪声功率。R1表示认知用户未检测到授权用户时的吞吐量(此时授权用户已出现)。

式中，C1为授权用户出现时的系统的吞吐量，其表达式为:

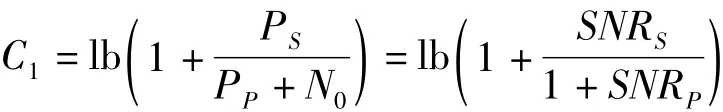
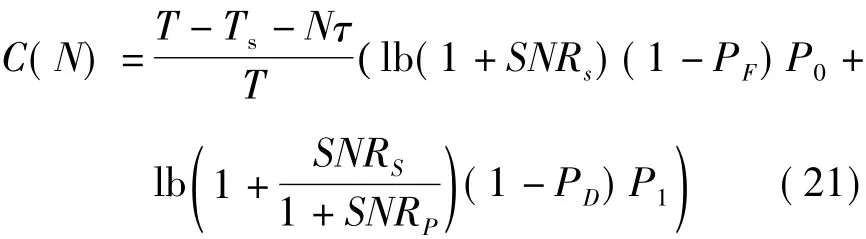
根据IEEE 802．22的标准，在信噪比SNR为-20 dB时探测概率PD≥90% ，而且当授权用户出现的概率值相对比较小时P1＜0．3，此时R1＜＜R0，因此可将R1忽略不计。

2 文中提出的优化算法

本文将能量效率的优化算法分为了两步进行:通过最小化整个协作频谱感知用户对能量的消耗来优化参与感知用户的数量和通过最大化整个协作频谱感知系统的吞吐量来优化参与感知用户的数量以达到最大化系统的能量效率。我们为了最优化系统的性能，将这两者一起考虑，对这两步进行折衷以取得最好的系统性能，以下是算法表达式:

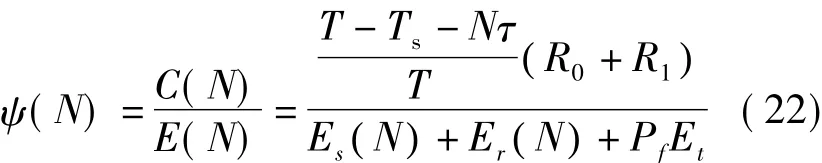
将式(10)与式(21)代入式(22)可得:

在这里若要得到N的最优值是非常困难的，因此考虑到使用迭代二分法［17］。因为N是一个有界的数，根据式(17)得出的数据，可以用如下方法得出最优的参与频谱感知的用户数量来使能量效率最大:

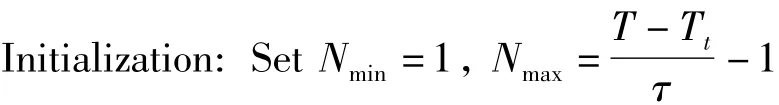
Define i=1

Compute μ(N-1)，μ(N)and μ(N+1)

ifμ(N+1) ＞ μ(N) ＞ μ(N-1)then Nmin=N

end

ifμ(N+1) ＜ μ(N) ＜ μ(N-1)then Nmax=N

end

ifμ(N+1)≤μ(N)＆μ(N)≥μ(N-1)then N0=N，i=0

end

3 仿真结果和分析

假设在一个认知用户数量为NT的认知无线网络的环境下。认知用户接收到的信号的功率与噪声功率比为ζ=-20 dB，信号的带宽设置为6 MHz，帧长为50 ms。在频谱感知阶段，每个认知用户的采样频率为 fs=1 MHz，每次采用消耗的能量为 ρs=0．1 w。在传送感知结果阶段，每个认知用户消耗τ=0．1 ms的传送时间，每次传送消耗的能量为ρr=1 w。在数据传输阶段，数据传输率假设为Dt=200 kb/s，每次数据传输消耗的能量为ρt=1 w。参与频谱感知的认知用户数量设为24。

图2是在探测概率门限PthD=0．8的情况下，系统在参与感知的认知用户数量变换时对应的系统平均能量消耗。对于4种不同的Tr+Ts，系统的能量消耗是一个关于N的凹函数，当系统的认知用户数量增加时，系统的能耗会逐渐增加，但是，由于每一帧的时间的约束，在本地感知和数据传输的方面消耗的能量将会减少。

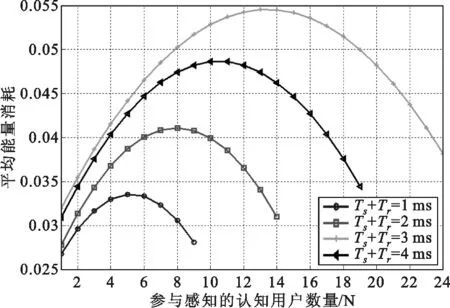
图2 参与感知的认知用户数量变换时对应的系统平均能量消耗

图3是在不同的探测概率门限下，与不同的Tr+Ts相对应的系统最小能量消耗的情况。可以明显的看出，探测概率门限越低，系统所消耗的能量越多，探测概率门限越高，能量消耗越少。随着Tr+Ts的增加，系统消耗的能量逐渐增加，但是到一定的值以后，系统消耗的能量会慢慢减少，这是因为在此情况下，数据传输阶段所消耗的能量减小了。

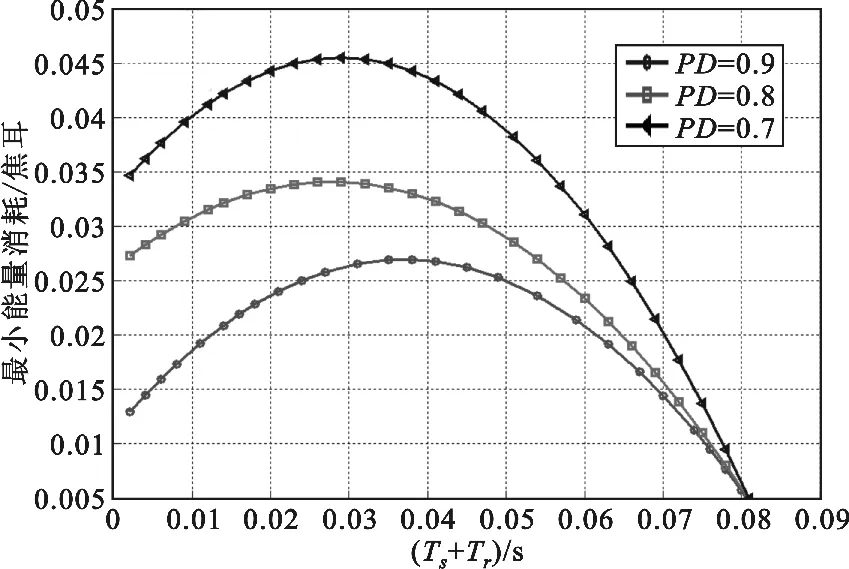
图3 不同的PthD值对应不同的(T s+Tr)值下的最小能量消耗

图4 是在不同的Tr+Ts值下，参与感知的认知用户数量与归一化的吞吐量形成的对应值。从图中可以看出，Tr+Ts的值越大，系统的归一化吞吐量相对越大。在参与感知的认知用户数量刚增加的阶段，系统的吞吐量先是增加，当数量达到一定的量后，系统的虚警概率降低、探测概率升高。根据式(21)系统的吞吐量会逐渐减小。

图4 不同的(T s+Tr)值对应的参与感知的认知用户数量所获得的归一化吞吐量

图5 是不同的能量效率优化方案在相应的探测概率下的取值。可以看出，探测概率的精度越大，本文所列的方案的能量效率明显高于本文所列举的单个优化方案和文献［18］所提出的优化方案。

图5 本文所述算法(23)与式(17)和文献［18］的所提的能量效率优化方案在相应的探测概率下的取值

4 结语

本文在固定的帧结构时间下，对协作频谱感知优化进行了研究。主要结论有:(1)在满足设定的探测概率的阈值情况下，通过优化参与感知用户数量从而使系统的吞吐量达到了最大;(2)在满足设定的探测概率的阈值情况下，通过优化参与感知用户数量从而使系统的能量消耗最小化;(3)通过一个二分法得出了最佳的参与频谱感知的用户的数量，从而使系统的能量效率达到最大。

本文与传统的优化能量效率方案相比，在优化的同时，更多考虑到了影响系统性能的吞吐量，在使用二分法求最优值算法中，更精确地得出了结论，使得本文所列算法更适合于求解考虑多个因素的复杂问题。:

［1］ Federal Communications Commission，Spectrum Policy Task Force，Rep［R］．ET docket．No．02-135，2002．

［2］ Federal Communications Commission，Spectrum Policy Task Force Report［R］．ET Docket No．02-155，Nov 02，2002．

［3］ Akyildiz IF，B FLo，Balakrishnan R．Cooperative Spectrum Sensing in Cognitive Radio Networks:A Survey［J］．Comput Phys Commun，11(2011)40-62．

［4］ Bhattacharjee Sh，Sengupta S，Chatterjee M．Vulnerabilities in Cognitive Radio Networks:a Survey［J］．Comput Phys Commun，36(2013)1387-1398．

［5］ Tani Y，Saba T．Quantization Scheme for Energy Detector of Soft Decision Cooperative Spectrum Sensing in Cognitive Radio［J］．IEEE GLOBECOM，2010，1387-1398．

［6］ Lee C，Wolf W．Energy Efficient Techniques for Cooperative Spectrum Sensing in Cognitive Radios［J］．IEEE CCNC，2013．

［7］ Lunden J，Koivunen V，Huttunen A，Poor H．Collaborative Cyclostationary Spectrum Sensing for Cognitive Radio Systems［J］．IEEE Trans．Signal Process．57(11)(2009)4182-4195．

［8］ Althunibat S，Narayanan S，Di Renzo M，Granelli F．On the Energy Consumption of the Decision-Fusion Rules in Cognitive Radio Networks［J］．IEEE CAMAD，2012，pp．17-19，125，129．

［9］ SUN C，ZHANG W，Ben K．Cluster-based Cooperative Spectrum Sensing in Cognitive Radio Systems［J］．IEEE ICC-2007，2012，pp．2511-2515．

［10］ Pham H N，ZHANG Y，Engelstad P，Skeie T，Eliassen F．Energy Minimization Method for Optimal Cooperative Spectrum Sensing in Sensor-Aided Cognitive Radio Networks［J］．ICST WiCON，2010，p．19．

［11］ Althunibat S，Palacios R，Granelli F．Energy-Efficient Spectrum Sensing in Cognitive Radio Networks by Coordinated Reduction of the Sensing Users［C］．IEEE ICC，Ottawa，Canada，2012．

［12］ Adelantado F，Juan A，Verikoukis C．Adaptive Sensing User Selection Mechanism in Cognitive Wireless Networks［J］．IEEE Commun．Lett．14(9)(2013)．

［13］ Mishra SM，Sahai A，Brodersen R．Cooperative Sensing Among Cognitive Radios［C］．IEEE International Conference in Communications(ICC06)，Turkey，vol．4，2006，pp．1658-1663．

［14］ 兰昆伟，赵杭生，李湘洋．认知无线电中基于感知门限的频谱预测研究［J］．通信技术，2015，47(02):1002-0802．LAN Kun-wei，ZHAO Hang-sheng，LI Xiangyang，Prediction Research based on Spectrum Sensing Threshold in Cognitive Radio Spectrum ［J］．Communications Technology，2015，47(02):1002-0802．

［15］ Peh E CY，LIANG Y C，GUAN Y L，ZENG Y．Optimization of Cooperative Sensing in Cognitive Radio Networks:A Sensing-Throughput Tradeoff View［J］．IEEE Trans．Veh．Technol．58(9)(2014)5294-5299．

［16］ Srinivasa S，Jafar S A．Cognitive Radios for Dynamic Spectrum Access-the Throughput Potential of Cognitive Radio:a Theoretical Perspective［J］．IEE Commun．Mag．45(5)(2007)73-79．

［17］ Richard L Burden，Douglas Faires J，Numerical Aanalysis［M］．PWS-Kent Pub．Co．，c1993，5th，ed．

［18］ 秦臻，薛峰，梁继民．最大系统效用合作频谱感知优化算法［J］．信号处理，2013，29(02):1003-0530．QIN Zhen，XUE Feng，LIANG Ji-min．Cooperative Spectrum Sensing Optimization Algorithm of Maximum System utility［J］．Journal of Signal Processing，2013，29(0 2):1003-0530．