随机共振现象与微弱信号接收

石盛超，李广侠，李志强，朱文明，张卫同

（解放军理工大学通信工程学院天基信息教研中心，南京 210007）

随机共振现象与微弱信号接收

石盛超，李广侠，李志强，朱文明，张卫同

（解放军理工大学通信工程学院天基信息教研中心，南京 210007）

本文从随机共振（Stochastic Resonance）可增强信号信噪比的现象出发，介绍了随机共振非线性双稳势阱模型和参数调节随机共振理论。在此基础上，分析了随机共振现象在微弱信号接收中两种可能的应用途径，通过仿真验证了应用的可行性。最后，分析提出了将随机共振理论应用于弱信号接收需要突破的三大关键技术，即：大参数信号变尺度与还原技术、参数自适应调节技术和调制信号随机共振技术，还提出了初步解决的思路。为拓宽随机共振现象的应用领域和探究解决低信噪比条件下的信号接收提供新的方法和途径。

随机共振；微弱信号接收；低载噪比；参数调节

1　引言

意大利学者R.Benzi在研究古气象冰川演化问题时发现：在过去的70万年中，地球的冰川期和暖气候期大概以10万年为周期交替出现。对这一时期地球气候的研究结果表明，地球绕太阳转动偏心率的变化周期大约为10万年，这意味着太阳对地球施加了周期信号。然而，这一周期信号本身很小，不足以使地球气候产生从冰川期到暖气候期的大幅度变化。为此，1981年R.Benzi［1］-［3］等人首次提出了随机共振的概念，对这种现象进行了很好的解释，他们认为这一周期信号与地球本身能够产生冷态和暖态的非线性条件，以及地球所受到的随机力（如太阳的各种无规则变化）三者之间达到了协同，通过随机共振引起了地球古气象的大幅度变动。

随机共振理论一经提出，不仅得到了物理、化学、生物医学、控制、通信和传感等自然科学界的关注，甚至被用于解决经济和社会科学界面临的一些关键问题，成为近三十年来持续的研究热点。

随机共振理论［4］-［7］指出，当淹没在强噪声背景中的微弱信号通过一个非线性系统时，当非线性系统、信号和噪声达到匹配时，噪声的能量会增强信号，使得处理后的信号信噪比增加。这为丰富信号检测方法提供了新的思路。与传统经典的消除或者抑制噪声的处理方法不同，一般的随机共振用于弱信号检测的方法［8］-［13］是：设计基于随机共振的非线性检测器，通过调整系统参数或改变进入检测器的噪声，使得非线性系统、信号和噪声达到随机共振状态，以随机共振输出信号为依据，可以实现微弱信号检测的目的。

2　随机共振理论

随机共振现象发生的三个基本要素是非线性系统、输入信号和噪声。考虑最简单的非线性双稳态系统，它可以由朗之万（langevin）微分方程［8］-［13］描述，如式（1）所示：

式中，x（t）为随机共振系统输出信号；s（t）为输入信号；a和b为正值的系统参数；n（t）为加性高斯白噪声，且满足E［n（t）］=0，D［n（t）］=σ2。

定义V（x）为双稳态系统的势函数，当不存在周期信号s（t）时，其表达式为：

，一个势垒点xb=0，如图1所示。但是当系统输入周期信号时，势函数会随着周期信号的变化而发生变化，如图2所示。

从力学角度出发，式（1）可用一个布朗粒子在双稳态势阱中的运动来形象地解释。当周期信号不存在时，势函数左右对称，噪声驱动粒子在其中一个势阱内随机波动，或者能够跃过势垒以克莱默斯（Kramers）速率在两个势阱之间来回穿梭。当加入周期信号后，势函数的变化导致势阱具有了非对称性，粒子从高势阱跃迁到低势阱的概率变大。在适量噪声能量的帮助下，当粒子来回跃迁周期与信号周期一致时，就出现了噪声、微弱信号和粒子运动协同的现象，这就是随机共振。

图1　双稳系统势函数图

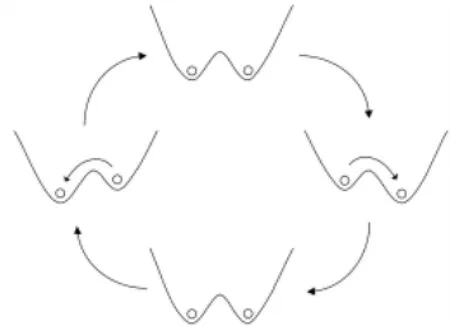
图2　双稳系统势函数变化图

在研究的早期阶段，噪声调节随机共振得到了较多关注，即通过改变噪声强度来实现非线性系统的随机共振。而在实际应用中，噪声调节随机共振方法可操作性较差，并且当噪声的强度已经超过发生随机共振的阈值条件时，进一步增加噪声强度只会使系统性能恶化，而减小噪声强度在实际应用中又难以实现。这样，通过调节参数来实现随机共振的理论［14］应运而生。

Xu［14］等于2002年提出了参数调节随机共振理论。简单地说，参数调节随机共振就是对于确定的输入信号和加性噪声，通过调节非线性系统的参数，逐步改变最小势高的值，促使发生随机共振。Duan等［14］的研究证明，增加噪声产生的随机共振现象和通过参数调节随机共振的现象具有一致性，调节参数相应地调节噪声的大小。

仍然考察双稳态系统，对系统作如式（3）变换

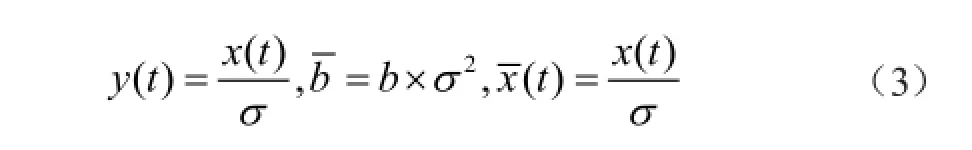
则方程（1）变为

式（4）所示的双稳态系统的势函数为：

势垒的高度为

式（6）说明，增大噪声强度σ和增大系统参数b均可降低系统势垒的高度，二者具有相同的调节效果。参数调节可以更灵活地改变最小势高，进而加速粒子实现成功跃迁的概率，随机共振现象就得以发生。参数调节随机共振既可以加强非线性系统的作用，又可以减弱非线性系统的作用。

3　两种基于随机共振的微弱信号接收方法

强噪声背景下微弱信号的接收一直是通信中亟需解决的问题。常规的微弱信号检测方法主要是基于时域和频域两种，有时域的相关方法、取样积分方法和频域的谱分析方法等。然而，这些方法都有一定的局限性，主要表现在所能检测到的微弱信号的信噪比门限值较高。因此，人们一直在寻找新的微弱信号接收方法以弥补传统方法的不足。随机共振现象中噪声增强信号的特性给研究人员提供了新的微弱信号接收的思路，对于噪声由传统的抑制噪声变为随机共振处理中利用噪声。将噪声N（t）和信号S（t）同时通入非线性处理器，调节系统参数使非线性系统、信号和噪声产生随机共振，继而从系统输出信号y（t）中提取信号。

基于现有的相关研究工作［10］［20］，将随机共振理论应用于微弱信号接收有两种基本的方法和途径：单频微弱信号随机共振接收；基带微弱信号随机共振接收。两种方法分别描述如下：

根据单频信号的频谱特点，在对单频信号进行接收中，往往对随机共振系统的输出信号 进行频谱分析，并以此来恢复单频信号得到 。具体原理框图如图3所示。

图3　基于随机共振的单频信号接收原理框图

将噪声N（t）和信号S（t）同时通入随机共振模块，通过调节系统参数a和b使系统达到随机共振，然后对随机共振模块的输出信号进行频谱分析得到单频微弱信号的频率特性进而恢复单频信号，随机共振模块的原理框图如图4。图中，（A）子模块是加法器，能够对输入信号及输出信号的反馈叠加；（B）子模块是积分器，起到对叠加信号的积分作用；（C）子模块是一个运算器，对输出信号进行立方运算并且取反；（D）（E）子模块均是倍乘器。可见，输入信号与输出信号的a次倍以及输出信号取反后立方值的b次倍共同经过积分，最终得到经随机共振作用的输出信号。这与朗之万方程是吻合的。

图4　参数调节随机共振模块原理框图

为了验证方法的有效性，本文选取频率f=20Hz的单频信号，在信噪比SNR=-18dB条件下进行了仿真，时域仿真结果如图5。

图5　单频信号随机共振处理时域效果图

仿真结果显示，通过随机共振处理之后的加噪单频信号，部分噪声能量转化为信号能量，淹没在强噪声下的信号特征恢复效果明显。

（2）基带微弱信号随机共振接收

早期随机共振处理的信号仅仅局限于周期信号，20世纪90年代初，Collins［19］提出了非周期随机共振的理论，对描述系统特性的朗之万方程进行了修改如式（7），取得了很好的效果。

非周期随机共振理论的提出使得随机共振与信息理论结合起来，人们将随机共振用于强噪声背景的微弱基带信号接收，取得了很好的效果，基本原理框图如图6。

印度消费的石油有多达80%为进口石油，这使得它面对价格波动时比其他进口国更加脆弱。最近几个月，由于卢比贬值导致石油进口价格膨胀，更加剧了其脆弱性。八月，印度政府估算，如果石油价格居高不下，2018/2019财年的进口石油支出将上升至高达260亿美元。

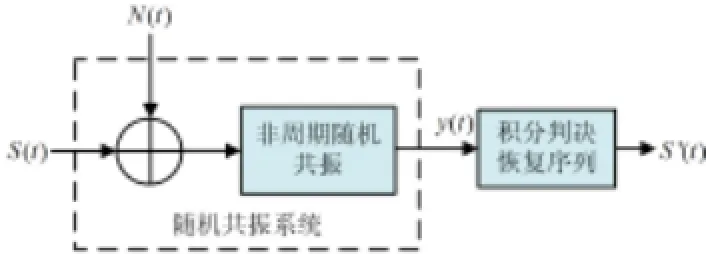
图6　基于随机共振的基带信号接收原理图

将噪声N（t）和信号S（t）同时通入非周期随机共振模块，通过调节系统参数A使系统达到随机共振，然后对随机共振输出信号进行积分判决恢复信息序列。为了适应非周期信号特性，对随机共振模块进行了相应的修改，具体结构如图7，取消了立方取反模块之后的倍乘器，在输入端增加（D）相乘取反模块，这与修改后的朗之万方程相对应。

图7　非周期随机共振模块原理框图

图8　基于随机共振的PAM信号接收

本文对比特率r=1000b/s，噪声方差σ2=16的PAM信号进行了仿真，具体结果如图8。仿真结果表明经过随机共振处理之后PAM信号得到了很好的恢复。

4　需突破的关键技术与初步思路

虽然随机共振现象应用于微弱信号检测可取得优于传统微弱信号检测的效果，但是发生随机共振现象有着苛刻的前提条件：信号必须是慢变信号并且振幅不能过大。因此，为了将随机共振理论应用于实际通信、导航或其他信息传输系统，必须突破以下三个关键技术：为了突破传统随机共振小参数条件的限制，必须研究新的变尺度随机共振算法；为了应对信号未知且多变的实际情况，实现对信号的快速捕获与连续跟踪，必须研究适用于信号传输的自适应随机共振算法；针对通信系统中常用的调制方式（如PSK，FSK，MSK等），必须研究相应的调制信号随机共振处理方法。

（1）大参数信号变尺度随机共振算法

针对通信信号是大参数的特点，研究将大参数信号变换到小参数信号从而触发随机共振的变尺度算法。在研究二次采样算法［17］［18］的基础上，提出一种基于互质欠采样的变尺度随机共振算法，使该算法适用于通信系统随机共振传输系统。

对加噪信号进行采样，采样频率为：

采用互质欠采样的方式对第一次采样得到的序列进行欠采样，欠采样频率为：

N，M互质，且满足：

采用互质欠采样得到的类小信号频率为：

选择合适的采样系数N和M，可以使类小参数信号满足随机共振条件。对小参数信号进行随机共振处理得到频率信息后，即可再按公式还原大参数信号。

（2）参数自适应随机共振技术

针对通信中信号和噪声的不确定性问题，研究提出新的自适应随机共振算法。根据随机共振的输出，以输出信噪比、波形与原始波形相关性、互信息量等为性能准则，自适应地调节系统参数。在可实现计算复杂度的基础上，能够完成信号的快速捕获和动态跟踪，满足通信系统信息可靠传输的需求。

针对已有的自适应随机共振算法冗余度高、计算量大等问题，拟在随机共振处理前增加自适应预调节模块，根据对噪声强度和信号频率的初步估计调整系统参数，在随机共振处理后的自适应再调节模块根据输出的信号进行再调节，最终实现随机共振。具体结构如图9所示。

图9　双自适应参数调节随机共振示意图

（3）通信系统调制信号随机共振算法

针对通信系统中典型的调制方式（PSK，FSK，MSK等），研究与随机共振结合进行信息传输的可行性，分析可获得的性能增益，通过比较，得出适合于通信系统调制信号随机共振的调制方式。

宽带调制信号信息速率高，频谱带宽较宽，这使得随机共振的增强作用并不明显。据此，在发端加入弱导频或残留载波辅助，在接收端对导频信号或残留载波进行随机共振处理，以此进行载波恢复，用于调制信号解调，具体结构如图10所示。

图10　有辅助导频PSK调制信号随机共振

窄带调制信号瞬时频谱为窄带，可直接对窄带调制信号进行随机共振处理，具体结构如图11所示。

图11　无辅助导频FSK调制信号随机共振

5　总结与展望

随机共振理论在非线性信号处理中发挥着重要的作用。通过建立参数调节双稳随机共振模型，文章对现有的基于随机共振的微弱信号接收的两种常见途径分别进行了计算机仿真，仿真结果表明了基于随机共振的微弱信号接收方法的有效性和在此应用领域的巨大应用前景。

经典随机共振理论只能够适用于慢变弱信号，这大大限制了随机共振的应用范围。为此，本文针对提出的需要突破大参数信号变尺度随机共振、参数自适应随机共振和调制信号随机共振三大关键技术，在现有研究成果的基础上，分别提出了初步的解决方案，为下一步问题的解决提供了参考。

随机共振理论和关键技术的不断完善势必将大大拓宽随机共振应用范围，为探究解决低信噪比条件下的信号处理提供新的思路和途径。

［1］R.Benzi，A.Sutera，and A.Vulpiani，“The mechanism of stochastic resonance ”. J.Phys. A：Math. Gen. 14（1981） L453-L457

［2］R.Benzi， “Stochastic resonance in climatic change”，Tellus，IEEE，vol.34，pp.10-16，1982

［3］B.McNamara and K.Wiesenfeld，“Theory of stochastic resonance”Physical Review A， vol.39， no.9， pp.4854-4869，May 1989

［4］S.Mitaim and B.Kosko，”Adaptive stochastic resonance”，Proceedings of the IEEE， vol.86， no.11， pp.2152-2183，Nov.1988

［5］F.C.Blondeau，”Input-output gains for signal in noise in stochastic resonance”，Elsevier Physics Lettersm232（1997）：41-48

［6］K.Loerincz，Z.Gingl，L.B.Kiss，”A stochastic resonator is able to greatly improve signal-to-noise ratio”Elsevier Physical Letters A，224（1996）：63-67

［7］Z.Ginal，L.B.Kiss，and F.Moss，”Non-dynamical stochastic resonance：theory and experiments with white and arbitrarily coloured noise”，Europhys.Lett.29（3），pp.191-196，1995

［8］杨祥龙，汪乐宇.随机共振技术在弱信号检测中的应用.电路与系统学报，2001，6（2）：94-97

［9］段江海，宋爱国，王一清.随机共振理论在微弱信号检测中的应用研究.信号处理，2003，19（6） ：569-572

［10］梁军利，杨树元，唐志峰.基于随机共振的微弱信号检测.电子与信息学报，2006，28（6）：1068-1072

［11］何大海，赵文礼，梅晓俊.基于随机共振原理的微弱信号检测与应用.机电工程，2008，25（4 ） ：71-74

［12］H.Chen.P.K.Varshney，S.Kay，and J.H.Michels， ”Theory of the stochastic resonance effect in signal detection：part I-fixed detectors” IEEE Trans. Signal process.，vol.55，no.7，pp.3172-3184，July，2007

［13］H.Chen.P.K.Varshney， ”Theory of the stochastic resonance effect in signal detection：part I-variable detectors”， IEEE Trans .Signalprocess.，vol.56，no.10，pp.5031-5041，Oct，2008

［14］Xu Bohou， Duan Fabing， Bao Ronghao， et al. Stochastic resonance with tuning system parameters：the application of bistable systems in signal processing［J］. Chaos， Solitons&Fractals， 2002， 13（4）：633-644

［15］F.Duan，D. Abbott，”Binary modulated signal detection in a bistable receiver with stochastic resonance”，Physica A：Statistical Mechanics and its Applications，2007；376：176-190

［16］F.Duan，B.Xu，”Parameter-induced stochastic resonance and baseband binary PAM signals transmission over an AWGN channel”，International Journal of Bifurcation and Chaos，vol.13，no.2（2007）411-425

［17］Leng Y.G.，Leng Y.S.，Wang T.Y.，et al，“Numerical analysis and engineering application of large parameter stochastic resonance”，Journal of Sound and Vibration，2006，292（3-5）：788-801

［18］Leng Y.G.，Wang T.Y.，Guo Y.，et a1.，“Engineering signal processing based on bistable stochastic resonance”，Mechanical System and Signal processing，2007，21：138-150

［19］J.J.Collins，Carson C. Chow，and Thomas T. Imhoff. “Aperiod stochastic resonance in excitable systems， ”Phys. Rev. E，1995，52（4），：R3321-3324

［20］段法兵.参数调节随机共振在数字信号传输中的应用.博士学位论文.浙江大学，2002

Stochastic Resonance Phenomenon and Weak Signal Receiving

Shi Shengchao， Li Guangxia， Li Zhiqiang， Zhu Wenming， Zhang Weitong
（College of Communications Engineering PLA University of Science and Technology， Nanjing， 210007）

On the basis of the phenomenon that Stochastic Resonance （SR） can enhance the signal noise ratio （SNR）， the Stochastic Resonance nonlinear Bistable-well model and parameter-induced Stochastic Resonance theory are introduced in this paper. Moreover， two weak signal receiving methods based on Stochastic Resonance are analyzed and simulation results are given. In addition， three key techniques including the scale-transforming SR algorithm， the adaptive parameter-adjusting SR algorithm and the SR algorithm for modulated signal are proposed. The elementary solving ideas are also put forward. The related researches will broaden the application area of Stochastic Resonance and provide novel ways for weak signal receiving under very low signal noise ratio circumstance.

stochastic resonance； weak signal receiving ； low carrier to noise ratio （CNR） ； parameter-induced

10.3969/j.issn.1672-7274.2015.03.003

TN75，TN85

A

1672-7274（2015）03-0013-06

国家自然科学基金资助项目（61032004，91338201）；国家高技术研究发展计划（“863”计划）资助项目（2012AA121605，2012AA01A 503，2012AA01A510）。