基于Matlabatlab的FIRFIR数字滤波器设计

郭天赐

（河南大学欧亚国际学院，河南　开封　47755000011）

基于Matlabatlab的FIRFIR数字滤波器设计

郭天赐

（河南大学欧亚国际学院，河南开封47755000011）

FIR数字滤波器是数字信号处理的一个重要组成部分，由于FIR数字滤波器具有严格的线性相位，因此，在信息采集和处理过程中得到了广泛的应用。本文介绍了FIR数字滤波器的概念，并在分析三种设计方法原理的基础上，借助Matlab仿真软件工具分别实现窗函数法、频率采样法和等波纹逼近法设计FIR滤波器。

数字滤波器；FIR滤波器；设计

现实中我们经常接触的信号有很多种。对于信号的各个应用，滤波器是必不可少的一种工具。选用合适的滤波器对产品的质量有一定的提升作用。同样，不适合的滤波器将影响产品的使用。

1　FIR滤波器及其设计方法

1.1FIR滤波器的基本概念

FIR滤波器即冲激响应是有限单位长的滤波器，是一个稳定的系统。因此，FIR滤波器在生活的各个方面都有广泛的应用。

1.1.1FIR滤波器的优点

①对于严格的线性相位要求能简单地完成，同时被处理的信号产生可减少相位失真；

②可得到多带幅频特性；

③极点全部在原点（永远稳定），无稳定性问题；

④总是满足因果性；

⑤无反馈运算，运算误差小。

1.1.2FIR滤波器的缺点

①因为无极点，要获得好的过渡带特性，须以较高的阶数为代价；

②需要计算机辅助设计以使程序完成。

1.2数字滤波器的设计方法

FIR数字滤波器有很多设计的方式，其中较为常用的是频率采样设计法、窗最优化设计法和函数设计法。本文主要论述利用窗函数法、频率采样法和等波纹切比雪夫逼近法来实现FIR滤波器的多种设计。

2　FIR数字滤波器设计

FIR数字滤波器设计过程一般包括以下基本问题：

①根据实际要求确定数字滤波器性能指标；

②用一个因果稳定的系统函数去逼近这个理想性能指标。

2.1窗函数法

窗函数法从时域出发，传输函数的系数由截取一段理想滤波器的单位脉冲响应来表示，被称为设计FIR数字滤波器的最简单的方法。由于窗函数法设计FIR数字滤波器是在时域进行的，且理想单位脉冲响应一般是非因果、无限长的，这就需要截取，截取的方法就是加窗。Matlab工具箱中加入了许多的窗函数，其中三角窗的最小阻带值为25db、主瓣宽度为8π/M、精确过度带宽6.1π/M，矩形窗最小阻带值为21db、主瓣宽度为4π/M、精确过度带宽1.8π/M，布拉克曼窗最小阻带值为74db、主瓣宽度为12π/M、精确过度带宽为11π/M，切比雪夫窗最小阻带值为21db、主瓣宽度为4π/M、精确过度带宽为1.1π/M，汉宁窗最小阻带值为44db、主瓣宽度为8π/M、精确过度带宽为6.6π/M，海明窗最小阻带值为53db、主瓣宽度为4π/M、精确过度带宽为1.8π/M，凯塞窗最小阻带值为21db、主瓣宽度为4π/M、精确过度带宽为1.8π/M［1-2］。由频率相应Hd（ejw）求取冲击响应，即分析出系统的稳定性和耦合性，然后通过在Matlab上编写软件程序，从而设计出一个近似的频率响应，实现了硬件滤波器软件的设计。设计过程如下：

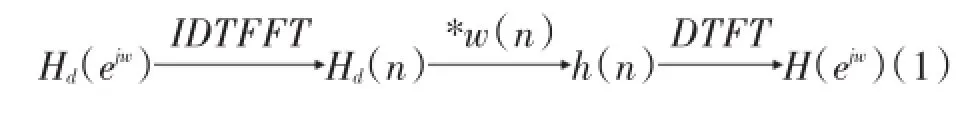
为了把理想滤波器的无限长脉冲响应hd（n）乘以窗函数w（n）来产生一个被截断的脉冲响应，人们使用了加窗的方法，即h（n）=hd（n）w（n），并且对频率响应进行平滑。

窗函数主要用来减少序列因截断而产生的Gibbs效应。为了克服这种现象，应该在设计窗函数时，滤波器的频率特性最大程度地降低主瓣宽度的数值，且能量要求尽可能不被浪费；窗函数频率特性中的ω越接近π其能量越接近零点［3］。

2.2频率采样法

频率采样法从频域出发，理想滤波器的频率响应为H（ejw），进行相同间隔的抽样，将得出的理想频率响应通过采样的方式得到hd（k）：

再利用Hd（k）可求得FIR滤波器的系统函数H（Z）及频率响应H（ejw），通过离散傅立叶反变换。而在各采样点间的频率响应则是其加权内插函数延伸叠加的结果。但在现实中信号大多是无限长的序列，插值逼近理论在实际应用中会有理想的频率响应曲线和理想的频率响应特性，内插函数的值越接近理想值，误差越小，逐步转变形状的近似误差，误差的大小，为此设计时需要随机地在不连续的区域添加不等量过度点。为了提高逼近的质量，可以通过在频率相应的过渡带内插入比较连续的采样点，从而使得通带和阻带之间变换比较缓慢，以达到减少逼近误差的目的。选取w∈［0，2π］内N个采样点的约束条件为：

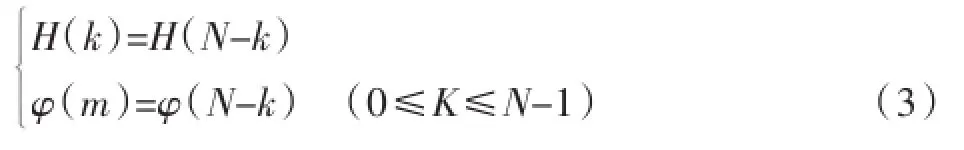
2.3等波纹逼近法

2.3.1等波纹切比雪夫逼近准则

对于通带和阻带的误差数值在滤波器的设计中有不同的要求。等波纹切比雪夫逼近准则通过对通带应用加权函数A，对阻带使用应用加权函数B，以此来实现相同的在不同频段的（通常指的是通带和阻带）加权误差最大值，从而实现滤波器最大误差在满足性能指标的条件下达到最小值。

窗函数法与频率采样法在FIR数字滤波器的设计中被人们广泛地应用，但两者均无法成为最优化的设计，被广泛应用的原因是因为考虑到成本与使用的问题。通常情况下线性相位滤波在不同的频带内逼近的最大容许误差要求不同。即使得Hd（ejw）和H（ejw）之间的最大绝对误差最小［4］。

等波纹切比雪夫逼近是采用加权逼近误差E（ejw），它可以表示为：

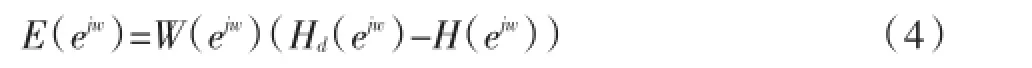
其中，W（ejw）为逼近误差加权函数在误差要求高的频段上，可以取较大的加权值，否则，应当取较小的加权值。

虽然按照FIR数字滤波器单位取样响应h（n）的对称性和采样点数的奇偶性，FIR滤波器可被分为不同类型的几种滤波器，但滤波器的频率响应的公式却是可以写成同样的式子：

其中，k∈｛0，1｝，H（ω）为幅度函数，且是一个纯实数，表达式也可以写成统一的形式：

其中，Q（ω）为ω的固定函数，P（ω）为M个余弦函数的线性组合［5］。

2.3.2仿真函数

利用remezord和remez函数可以实现FIRDF的最优化设计，而且remezord和remez函数存在于数字信号处理工具箱中：

（1）n，f0，a0，weight=remezord（f，a，dev）

是用来代替remezord中的N，归一化频带边缘、频带的振幅频带振幅中存在的功能和在每个频带之内权重的加权系数的输入参数，它们代表不同的含义。

（2）h=reme（n，f0，a0，weight，′ftype′）

功能：利用remez函数可以得到最优化设计的FIR DF的h（n）系数，输入参数中滤波器的阶数由第一个数据n来表示。为了区分滤波器的类型，人们在最后加入ftype值来区分不同类型的滤波器。remezord函数的阶数n提升的高估或低估。因此在通过remezoed函数求出滤波器的系数后，对于阻带最小衰减的检测观察其是否满足设计要求［6］。如果此时的阻带最小衰减不能满足设计要求，那么就必须提高滤波器的阶数。

3　结果分析

在间断点处增加一个过渡点后的情况。可以看出滤波器的带外衰减指标有了明显的改善，但同时增加了滤波器的过渡带宽。

采样点上2/N点集中在指定的通带和阻带截止频率的整数倍的频率，这种方法受到一定的限制，相对而言，不够灵活。充分地提高N，对于任何给定的频率可以接近。但计算量和复杂性增加。频率采样法明显偏离设计指标，且相对来说更不易操作，只有过渡带样点值与实际相对出入较小时，衰耗特性才会取得令人满意的结果。

4　结论

在设计中，要使设计的滤波器的冲激响应同时满足预先设定的全部参数是十分困难的，如果该滤波器的特性不满足要求，但是原有参数必须做适当调整。这在程序中很容易实现，只需对参数M、δ1、δ2事先给定，允许ωp与ωs随着要求的改变而变化，就可以得到新条件下滤波器的特性。从而达到节约资源的效果。这样使得设计出来的滤波器更为简单经济。

相对于前两种滤波器的设计方法，等波纹逼近法有着无法忽视的优势。其不仅程序简单而且在实现中的应用层面也相对较宽广。当一个产品需要压缩程序空间时，对于滤波器设计模块最优化设计给出的滤波器必定是我们的首选方式。

［1］郭士剑，贺志国.Matlab7.x数字信号处理［M］.北京：人民邮电出版社，2008.

［2］程耕国，陈华丽.信号与系统实验教程（Matlab）版［M］.北京：机械工业出版社，2009.

［3］谢仕宏.Matlab R2008控制系统动态仿真实例教程［M］.北京：化学工业出版社，2005.

［4］徐昕，伯晓晨，等.Matlab工具箱应用指南——控制工程篇［M］.北京：电子工业出版社，2000.

［5］程耕国.信号与系统：上册［M］.北京：机械工业出版社，2009.

［6］程耕国.信号与系统：下册［M］.北京：机械工业出版社，2009.

Design of FIR Digital Filter based on Matlab

Guo Tianci
（Eurasian International College，Henan University，Kaifeng Henan 475001）

FIR digital filter is an important part of digital signal processing，due to its strict linear phase，so in the process of information acquisition and processing，it has been widely used.The concept of FIR digital filter is introduced in this paper，and based on the analysis of three design principles and methods，with the tool of MATLAB simulation software，FIR digital filter is designed by the window function method and frequency sampling method and the ripple approximation method respectively.

digital filter；FIR filter；design

TN713.7

A

1003-5168（2015）10-0042-3

2015-9-20

郭天赐（1995-），男，本科，研究方向：通信工程。