环网处理器阵列的容错重构技术*

祝龙婷，武继刚，姜桂圆，王 超

（1.天津工业大学计算机科学与软件学院，天津 300387；2.天津大学计算机科学与技术学院，天津 300072）

环网处理器阵列的容错重构技术*

祝龙婷1，武继刚1，姜桂圆2，王 超1

（1.天津工业大学计算机科学与软件学院，天津 300387；2.天津大学计算机科学与技术学院，天津 300072）

高效的容错技术对于提高多处理器系统的可靠性至关重要。环网（Torus）是连接多处理器阵列的重要网络结构，而环网处理器阵列上的容错重构技术目前尚属空白。针对环网阵列的特殊连接方式，将环网阵列重构问题转化为矛盾图上求解最大独立集问题。矛盾图上的结点表示故障处理器的替换方案，而边代表了不同替换方案之间的不可共存特性。主要是根据三种不同的冗余处理器分布方案，设计生成矛盾图算法，求解最大独立集算法，以及由独立集生成逻辑处理器阵列算法，取得了令人满意的结果。实验结果表明，当阵列规模较小或故障率较低时，一行一列和十字型的冗余单元分布的重构能力较好；而随着阵列规模或故障率的增大，三种冗余单元分布策略的重构成功率都随之下降，但可通过增加冗余单元以及调整冗余分布来改善容错效果。此外，从实验结果中还可以看出，环网处理器阵列的容错能力显然优于网格（Mesh）处理器阵列。

环网处理器阵列；重构算法；容错技术；矛盾图

1 引言

随着超大规模集成电路VLSI（Very Large Scale Integration）和晶片规模集成电路WSI（Water Scale Integration）技术的快速发展，在单一芯片上集成成百上千的处理器单元PEs（Processing Elements）成为可能。然而，随着VLSI集成密度的迅速增加，多处理器系统的可靠性成为越来越严峻的问题，因而高效的容错技术对于提高多处理器系统的可靠性至关重要。总体来说，有两类策略来进行容错重构：冗余策略和降阶策略。降阶策略的特点是原阵列中不存在冗余单元，要尽量多地使用无故障单元来生成逻辑阵列。前人证明了基于降阶策略的重构问题大都为NP完全问题，同时还提出了多种启发式的解决算法及相关改进。一个称为GCR（Greedy Column Rerouting）的算法［1］能够在限定选路距离的条件下得到在选定行上重构问题的最大逻辑阵列。文献［2］结合 GCR算法，提出一个有效的算法，通过减少逻辑阵列中的长连接来降低功耗。文献［3，4］分别采用4-端口和6-端口的通道，研究了在行列同时选路的模式下重构，目的都是获得尽可能大的逻辑阵列。此外，文献［5，6］将阵列的重构问题从二维推广到三维上，并分别提出了一种三维VLSI阵列上的启发式重构算法和非回溯的重构算法。文献［7］还使用多线程技术来加速重构算法速度。然而，只要阵列中存在故障，则得到的阵列的规模就一定会下降，而冗余策略的目标是保证最终逻辑阵列与原始阵列保持相同规模，进而保证计算性能不降低。冗余策略［8］中，物理阵列中预留了一定数量的冗余单元。当电路中某些处理单元不能正常工作时，使用预留的冗余单元来替换故障单元。文献［9］为基于网格连接的处理器阵列提供了一个自修复的电路，使用提前集成的冗余单元来替换故障单元，但这是通过面积和功耗来减少时间上的延迟，需要在面积、功耗和时间延迟间寻求一个合理的平衡。在冗余单元重构中，还存在不同的开关机制，文献［10］通过选择多通道开关来提高阵列的重构率，但是单通道开关显然占用硬件面积小且出现故障率低，故本文的研究与大多数以往研究一样，都是基于单通道开关的。

总结国内外的研究现状可知，阵列的容错重构技术正处于日益发展的阶段。尽管前人做出了很多这方面的研究成果，但目前的容错重构技术大多基于网格（Mesh）处理器阵列，对于环网（Torus）处理器阵列的容错重构方面的工作涉及较少，尤其是环网的冗余容错技术尚属空白。而近年来，环网互连网络越来越受重视，基于环网提出的可重构系统、映射算法、片上网络结构、路由算法等大量涌现［11，12］，这是因为与网格 相比，环网 具 有更 高的 通信性能。因而，本文研究基于环网处理器阵列的容错重构技术。本文将环网处理器阵列的容错重构问题转化为矛盾图上的最大独立集问题，并设计高效算法来实现矛盾图构造、最大独立集求解以及逻辑处理器阵列生成的过程。

2 基本定义及相关研究工作

2.1 物理阵列模型

令H表示原始物理阵列，H中含有故障单元，逻辑阵列是指重构后不含故障单元的阵列，称为T。对于给定的一个m×n的物理阵列H，用Nf表示阵列中所含故障单元的个数，对于第i个故障单元，用ei表示，则row（ei）表示第i个故障单元的物理行坐标，col（ei）表示第i个故障单元的物理列坐标，1≤i≤Nf。

本文所讨论的物理阵列包含处理单元、冗余单元、开关单元和连线。如图1所示是一个规模为2× 3的环网处理器阵列，在其上一行和左一列集成了冗余单元。容错重构的功能是通过向阵列中插入开关和连线实现的，开关和连线将每个处理单元连接在一起，从而使得阵列可以灵活地改变处理单元之间的连接方式。其中开关单元具有三种状态，这些状态可以根据阵列的需求进行切换。为了单独考虑处理单元的重构情况，本文做出了如下假设：

（1）故障单元能够转化为连接单元，即连线；

（2）开关单元、连线及冗余单元均不含故障。

Figure 1 Reconfigurable architecture图1 可重构结构

多数文献都采用假设（1）；而假设（2），因为开关单元和连线比处理单元有着更加简单的硬件结构，而冗余单元个数比处理单元要少得多，故相对于处理单元而言，可认为三者均不含故障。

为了更好地理解后面的内容，在此处介绍几个重要的概念。

（1）补偿通道。如果一个故障单元在物理位置（x，y）处存在故障，它可能被一个位置在（x1，y1）的正常单元 代 替，而 （x1，y1）又 被 另 一 个 位 置在（x2，y2）的正常单元代替，如此替换下去，直到一个冗余单元被利用时，替换过程结束。这个按物理单元的次序（x，y），（x1，y1），（x2，y2），…的替换过程就定义了一个补偿通道。

随着冗余单元分布的不同，每个故障单元可能有着不同个数的补偿通道。当冗余单元的分布如图1所示时，每个故障单元在理论上有两个可能的补偿通道，其方向分别是向上、向左，用［x—，y］、［x，y—］来表示。类似地用［x+，y］、［x，y+］表示补偿通道的方向向下、向右。

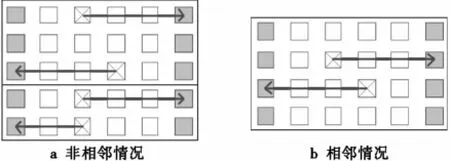
Figure 2 Replacement paths图2 相邻和非相邻补偿通道

（3）相交。包括两种情况：

①两个故障单元不在同一行或同一列上；

②两个故障单元位于同一行或同一列上。

图3a所示为两个故障单元既非同一行，也非同一列，图3b所示为两个故障单元位于同一行。

Figure 3 Intersect图3 相交

2.2 问题描述及以往研究工作

问题R 给定一个规模为m×n的环网连接的物理阵列H，H中还包含一定数量的冗余处理器单元。当H中部分处理器发生故障时，利用冗余处理器单元对故障处理器单元进行替换，得到一个m×n逻辑阵列。

为了构造有效的逻辑阵列，原始的m×n的物理阵列中所有故障单元都必须能够被冗余单元所替换，并且替换补偿通道间不能出现相交和相邻的情况。如图4所示，当故障单元u向右进行补偿，故障单元v向左进行补偿时，即为所定义的相邻情况，此时需要使用双通道进行布线才能实现（圆圈标记处），而本文所研究的是在单通道的情况下，因而不允许存在相邻情况。由于环网在水平和垂直方向上都有环绕，因此补偿通道上可以存在弯曲，但不可以有折线存在，即不允许某个故障单元被与其非同行或同列的冗余单元替换。此外，两个故障单元不能出现争用现象，即两个故障单元位于同一行或同一列上，而这一行或一列上只有一个冗余单元用于替换故障单元。

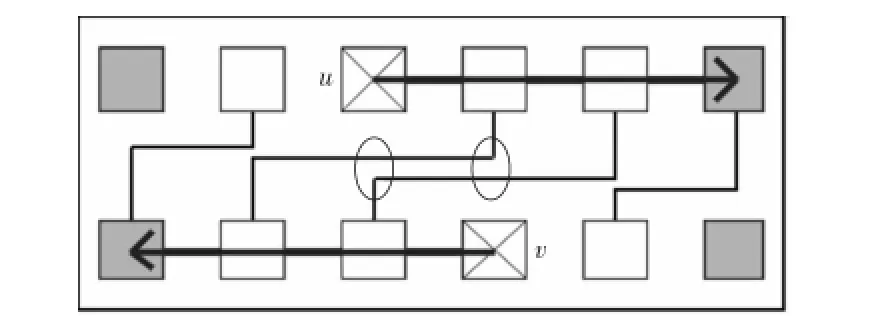
Figure 4 Adjacent relation of replacement paths图4 故障单元补偿通道间的相邻关系

3 基于矛盾图理论的重构算法

容错重构问题就是对于一个含有故障单元的物理阵列，为每一个故障处理器找到一个补偿通道，使得所有的故障处理器都可以被非故障处理器替换。本文将容错重构问题转化为矛盾图上求解独立集的问题：首先利用包含故障单元的物理阵列构造矛盾图，之后求解矛盾图的最大独立集，则可以得到对应的逻辑阵列。在本节将介绍如何将故障阵列转换为对应的矛盾图。给定物理阵列H，对H中任意一个故障单元ei（1≤i≤Nf），用Vi表示其所有可能的补偿通道方向的集合，即，其中分别表示上、下、左、右四个补偿通道方向。本文构造矛盾图G（V，E）如下：V是顶点集，每个顶点表示某个故障单元的一个补偿通道方向，E是边集。对于u，v∈V，当且仅当u、v不可共存时，u和v之间有边相连。

3.1 冗余单元呈上下两行分布

如图5a所示，物理阵列中包含上下两行的冗余单元，则每个故障单元有两个可能的补偿通道，其方向分别是向上和向下。该阵列包含四个故障单元，故有八个补偿通道供选择，即所构造的矛盾图将包含八个结点。

Figure 5 Physical arrays and the corresponding contradiction graphs图5 物理阵列与对应的矛盾图

本文提出的生成矛盾图G（V，E）的算法GCG （Generating Contradiction Graph）过程如下：对于H中的每个故障单元ei，将两个结点和加入到顶点集合V，其中和分别表示对故障单元ei采用向上补偿和向下补偿。矛盾图的边集E初始化为Ø，其构造过程如下：

（1）对于关联同一故障单元的顶点之间添加边，将这些边加入边集合E中；

（2）对于任意两个故障单元，若它们的补偿通道存在相邻关系（此处仅考虑列相邻），将相应顶点之间应添加的边加入到E中；

（3）对于任意两个故障单元，若一个故障单元的补偿通道上存在另一个故障单元，则存在相交关系，将相应顶点之间应添加的边加入到E中。因篇幅所限，GCG的伪代码已省略。

现在我们分析GCG的时间复杂度。生成矛盾图的算法GCG包含两个步骤，步骤1是添加结点到矛盾图中，显然步骤1可在线性时间完成；步骤2是生成矛盾图的边集，主要包括构造边集的三个过程：构造矛盾图边集的过程（1）可在O（Nf）时间内完成，Nf为故障单元个数；构造边集的过程（2）、（3），需要检查每个故障单元与其它故障单元之间的位置关系至多需要O（Nf·Nf）时间。因而，步骤2的时间复杂度上界为O（Nf·Nf）。综上，算法GCG的时间复杂度为O（）。

图5a展示了将一个包含两行冗余处理器的物理阵列转换为矛盾图的例子：首先，每个故障单元都有向上和向下两个可能的补偿通道方向，分别用两个点表示，因而矛盾图中有八个节点；然后按照边的生成规则，对相互矛盾的两个点之间添加边相连，最终得到的矛盾图如图5a下方所示。需要说明的是，顶点6和顶点7违反了相交规则中的一个故障单元的补偿通道上存在另一个故障单元，最后这两个顶点都不可能出现在正确的重构中，故使用虚线连接。

3.2 冗余单元呈一行一列分布

如图5b所示，物理阵列中包含一行一列的冗余单元，每个故障单元有四个可能的补偿通道，其方向分别是向上、向下、向左和向右。该阵列包含四个故障单元，所构造的矛盾图将包含16个结点。对应的矛盾图如图5b所示，上方为物理阵列，下方为对应的矛盾图。

生成矛盾图G（V，E）的过程如下：对于H中的每一个故障单元ei，将四个结点加入到顶点集合V，其中分别表示对故障单元ei采用向上补偿、向下补偿、向左补偿、向右补偿。矛盾图的边集E初始化为Ø，其构造过程如下：

（1）对于关联同一故障单元的顶点之间添加边，将这些边加入边集合E中；

（2）对于任意两个故障单元，若它们的补偿通道间存在相邻关系（包括列相邻和行相邻），将相应的顶点之间应添加的边加入到E中；

（3）对于任意两个故障单元，若存在相交关系（此处包括：①一个故障单元比另一个故障单元行数大列数大；②一个故障单元的补偿通道上存在另一个故障单元），将相应的顶点之间应添加的边加入到E中；

（4）当两个故障单元间存在争用同一冗余单元的现象时，将相应的顶点之间应添加的边加入到E中。

3.3 冗余单元呈十字型分布

如图5c所示，物理阵列中包含十字型分布的冗余单元，该十字型的冗余单元将物理阵列分成了

四个区间，按逆时针方向，从左上依次记为一、二、三、四区间。图5c上方所示的阵列包含四个故障单元，每个故障单元有四个可能的补偿通道，其方向分别是向上、向下、向左和向右，所构造的矛盾图将包含16个结点。生成的矛盾图如图5c下方所示。

生成矛盾图G（V，E）的过程与一行一列的情况类似。考虑到区间的问题，边的构造过程中的

（2）和（3）略有不同。具体变动如下，其中（2′）、（3′）分别对应于原步骤的（2）与（3）：

（2′）对于任意两个故障单元，若它们的补偿通道间存在相邻关系（包括列相邻和行相邻，同时要考虑两个故障单元是否处于同一区间），将相应顶点之间应添加的边加入到E中；

（3′）对于任意两个故障单元：

①两故障单元同区间时，与一行一列的相交情况一样；

②两故障单元不同区间时，按以下区间组合分别考虑：两个故障单元分别在（一、二）区间或（三、四）区间；两个故障单元分别在（一、四）区间或（二、三）区间；两个故障单元在（一、三）区间；两个故障单元在（二、四）区间，若存在相交关系，将相应顶点之间应添加的边加入到E中。

3.4 求解矛盾图的最大独立集

由于最大独立集问题是一个 NP完全问题，而蚁群算法是模拟蚂蚁觅食来寻求解的一种启发式算法，经常被用于求解组合优化这一类问题。故对于生成的矛盾图，本文设计了最大最小蚁群算法MMAS（Max-Min Ant System）来求其最大独立集，根据最大独立集可以判断该物理阵列是否能够重构。MMAS是一个以迭代的方式进行寻找全局最优解的过程，迭代过程中包括定义启发信息，设置状态转移规则和信息素更新策略。具体过程详见文献［13］。

4 基于最大独立集的生成逻辑阵列算法

本文提出的生成逻辑阵列的算法具体如下：首先，初始化逻辑阵列即为物理阵列。然后，以列为单位，按行号从小到大依次遍历每个非冗余单元，若该单元为故障单元，根据它的补偿通道方向判断该单元将被哪个单元替换，即重构后该单元的逻辑下标；如果该单元为非故障单元，检查该单元是否在列上用于替换了其它单元，若是，根据该单元所在补偿通道的方向决定其重构后的逻辑下标，否则就直接输出该单元的物理下标；如果该单元的逻辑下标与物理下标一致，再检查其是否在行上用于替换了其它单元，若是，根据该单元所在补偿通道的方向决定其重构后的逻辑下标，否则就直接输出该单元的物理下标。

生成逻辑阵列的伪代码Log Arr（Logical Array）如下：

现在我们分析该算法的时间复杂度。规模为m×n的处理器阵列上包含Nf个故障处理器。显然，在第1行（初始化）所需要的时间为O（m·n），这是因为处理器规模为m×n。在第2～11行，分别判断每个处理器，当其为故障处理器时，需要确定其补偿通道的方向，所花费时间为O（Nf）；当其为非故障处理器时，还要分别判断其在列上、行上是否用于替换其它单元，该操作分别需要的时间为O（Nf·m）、O（Nf·n）。因而，第2～11行的时间复杂度为O（m·n·max｛m，n｝·Nf），因为需要遍历的处理器个数为m×n。综上，算法Log Arr的时间复杂度为O（m·n·max｛m，n｝·Nf）。

需要说明的是，当冗余单元呈上下两行分布时，只需要考虑其在列上是否用于替换其它单元；而冗余单元呈十字型时，在计算其逻辑位置时，还要注意区间的考虑。

图6展示了当冗余单元呈一行一列分布时，其生成逻辑阵列的例子。图6a中单元r在u的补偿通道上，故单元u被r所替换。阵列中开关状态及连线如图6b所示，由于本文将故障单元直接转换成为连线，故在图中表现出来是直接用连线将故障单元穿过，而对于未使用的冗余单元本文也通过使用连线直接穿过来处理。

Figure 6 One-row-one-column distribution图6 冗余单元呈一行一列分布

5 实验与分析

本文编程使用的语言为C/C++，环境为Intel Core CPU 3.3 GHz 2 GB。为了客观公正地评价三种冗余分布的性能，在初始阵列中使用随机方法来产生故障单元，从而保证了实验数据的随机性。本文分别在特定的阵列规模和特定的故障率下，比较这三种冗余单元分布随着故障率的增高和阵列规模的增大，阵列重构率是如何变化的。本文将阵列重构率定义为30次实验中重构成功的概率，用Reliability表示；将三种冗余分布按上下两行、一行一列及十字型依次定义为case 1、case 2、case 3。

表1展示的是固定阵列规模分别为16×16和32×32时，三种冗余单元分布在不同故障率下的重构率。从表1中可以看出，在阵列规模一定的情况下，随着故障率的增加，三种冗余单元分布的重构率都有所下降。这是由于阵列规模不变，则冗余单元数量不变，而故障率增加使得故障单元数量增多，最终导致冗余单元无法满足替换全部故障单元的情况。例如，当故障率从3%上升到4%时，在阵列规模为16×16和32×32的情况下，三种冗余单元分布的重构率都下降了，其中上下两行的重构率下降最快，因为这种冗余分布的阵列只能在列上进行重构，故重构能力较差。

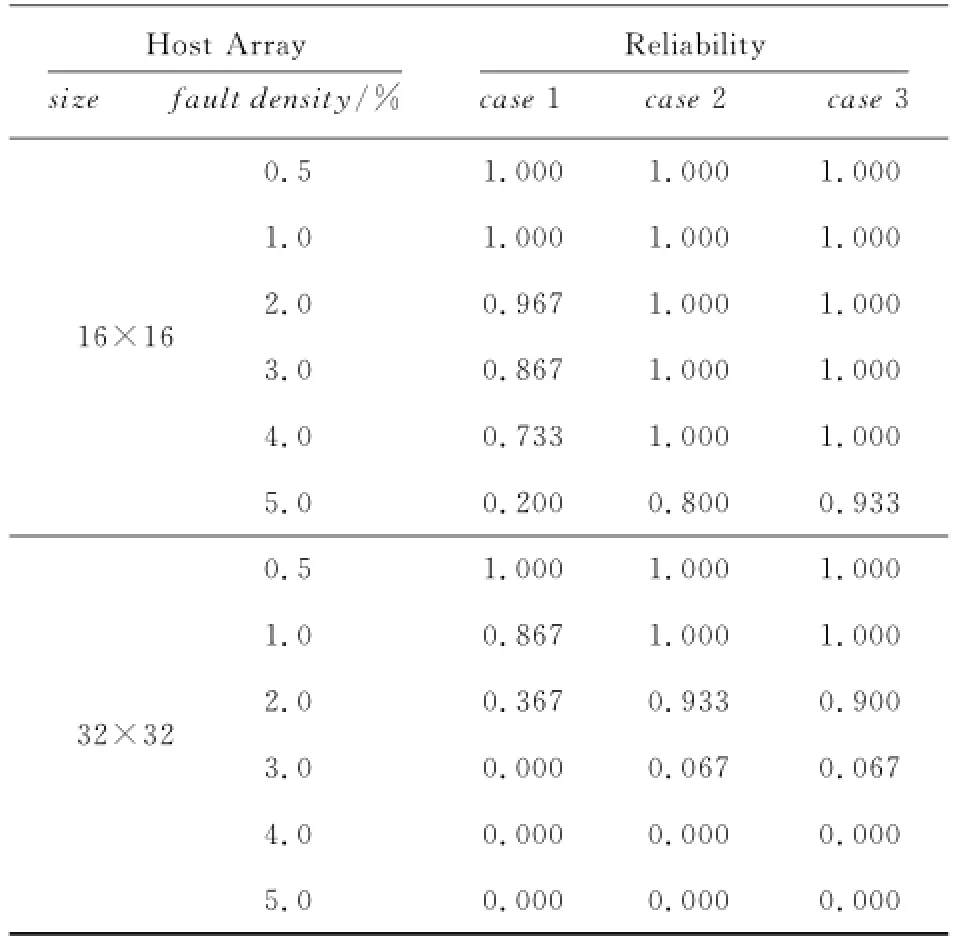
Table 1 Impact of fault density on reliability表1 故障率对重构成功率的影响

图7是将故障率设为8%，针对Mesh和Torus的三种冗余单元分布，在不同阵列规模下得到的重构率。从图7中可以看出，在故障率固定的情况下，随着阵列规模的增大，对于Mesh和Torus网络的三种冗余单元分布的重构能力都有所下降，尤其是上下两行的冗余单元分布下降得更明显。这是因为虽然阵列规模增大，使得冗余单元和故障单元同时都有所增大，但是由于冗余单元的分布情况使得故障单元数量比冗余单元数量增长得快，因而随着阵列规模的增加，三种冗余单元的重构能力都有所下降。例如，当阵列规模从8×8上升到16× 16时，三种冗余单元分布的重构率都有所下降。同时，从图7中可以看出，对于三种情况下的冗余分布，Torus网络比Mesh网络的重构成功率要高，这是因为Torus具有更灵活的连接方式，故比Mesh中的每个冗余单元有更多的机会选择替换哪个故障单元。需要说明的是，当阵列规模为16×16时，在图7a和图7b中，Mesh网络的重构率为0。

不同的冗余分布可以发现，当冗余单元数目为故障单元的两倍时，一行一列和十字型的冗余单元分布的重构能力较好，使得阵列具有较高的稳定性。

Figure 7 Reliability comparison of Torus and Mesh图7 Torus与Mesh重构率的对比图

6 结束语

本文在环网处理器阵列上，率先提出了基于矛盾图理论的容错方法。通过将故障单元的补偿通道方向表示成矛盾图的顶点集合，从而将故障阵列能否重构的问题转化为求解矛盾图的最大独立集问题，并对于能够重构的阵列提出了一种生成逻辑阵列的算法。实验结果表明，只要保证冗余单元数目为故障单元的两倍，就可以使得一行一列和十字型的冗余单元分布得到较好的重构率，使得阵列具有较高的稳定性。

在本文中，当故障单元增多时，重构率较低，这是因为摆放的冗余单元数较少。在接下来的工作中，作者计划研究更多的结点摆放方案，同时考虑按照不同的阵列规模设定不同的冗余方案，从而使得既不浪费大量的冗余单元，还能保证较好的重构率。

［1］ Low C P，Leong H W.On the reconfiguration of degradable VLSI/WSI arrays［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，1997，16（10）：1213-1221.

［2］ Wu J G，Srikanthan T，Jiang G Y，et al.Constructing sub-arrays with short interconnects from degradable VLSI arrays ［J］.IEEE Transactions on Parallel and Distributed Systems，2014，25（4）：929-938.

［3］ Wu J G，Srikanthan T.Integrated row and column re-routing for reconfiguration of VLSI arrays with 4-port switches［J］. IEEE Transactions on Computers，2007，56（10）：1387-1400.

［4］ Wu J G，Srikanthan T，Schroder H.Efficient reconfigurable techniques for VLSI arrays with 6-port switches［J］.IEEE Transactions on Very Large Scale Integration Systems，2005，13（8）：976-979.

［5］ Jiang G Y，Wu J G，Sun J Z.Efficient reconfiguration algorithms for communication-aware three-dimensional processor arrays［J］.Parallel Computing，2013，39（9）：490-503.

［6］ Jiang G Y，Wu J G，Sun J Z.Non-backtracking reconfiguration algorithm for three-dimensional VLSI arrays［C］∥Proc of the 18th International Conference on Parallel and Distributed Systems，2012：362-367.

［7］ Shen Y Z，Wu J G，Jiang G Y.Multithread reconfiguration algorithm for mesh-connected processor arrays［C］∥Proc of the 13th International Conference on Parallel and Distributed Computing，Applications and Technologies，2012：659-663.

［8］ Zhang L.Fault-tolerant meshes with small degree［J］.IEEE Transactions on Computers，2002，51（5）：553-560.

［9］ Takanami I，Horita T.A built-in circuit for self-repairing mesh-connected processor arrays by direct spare replacement ［C］∥Proc of the 18th Pacific Rim International Symposium on Dependable Computing，2012：96-104.

［10］ Horita T，Takanami I.Fault-tolerant processor arrays based on the 1.5-track switches with flexible spare distributions ［J］.IEEE Transactions on Computers，2000，49（6）：542-552.

［11］ Luo W，Dong X.An efficient adaptive deadlock-free routing algorithm for torus networks［J］.IEEE Transactions on Parallel and Distributed Systems，2012，23（5）：800-808.

［12］ Ramanujam R S，Lin B.Randomized throughput-optimal oblivious routing for torus networks［J］.IEEE Transactions on Computers，2013，62（3）：561-574.

［13］ Li Y M，Xul Z B.An ant colony optimization heuristic for solving maximum independent set problems［C］∥Proc of the 5th International Conference on Computational Intelligence and Multimedia Applications，2003：206-211.

祝龙婷（1990），女，安徽桐城人，硕士生，研究方向为高性能体系结构。E-mail：zlongting@gmail.com

ZHU Long-ting，born in 1990，MS candidate，her research interest includes high performance architecture.

Reconfiguration approaches for fault-tolerant torus-connected processor arrays

ZHU Long-ting1，WU Ji-gang1，JIANG Gui-yuan2，WANG Chao1
（1.School of Computer Science and Software Engineering，Tianjin Polytechnic University，Tianjin 300387；2.School of Computer Science and Technology，Tianjin University，Tianjin 300072，China）

High-efficient fault-tolerant techniques are essential for improving the reliability of multiprocessor systems.It is well known that torus is an important interconnection network for multiprocessor arrays，but no work has been reported on the faulty tolerance of torus-connected processor arrays.In our work，reconfiguring a torus-connected processor array is modeled to be a maximum independent set problem.The nodes on the contradiction graph represent alternatives of the fault processing elements （PEs），and the edge denotes that different alternatives cannot coexist.Three different distributions of redundant PEs are discussed，and three algorithms are proposed to construct contradiction graphs，solve maximum independent set，and generate logic arrays based on the produced maximum independent set. Simulation results show that，the cross distribution and one-row-one-column distribution perform well in reconfiguration for smaller arrays and smaller fault densities.In addition，the reconfiguration ability of the three proposed distribution patterns decreases as the fault density and array size increase，thus other spare distribution patterns should be investigated，or more spare PEs should be integrated.Moreover，torus arrays outperform mesh arrays in terms of fault-tolerance performance.

torus-connected processor array；reconfiguration algorithm；fault-tolerance；contradiction graph

TP303

A

10.3969/j.issn.1007-130X.2015.08.002

1007-130X（2015）08-1423-07

2014-08-11；

2014-10-11

国家自然科学基金资助项目（61173032）；国家自然科学基金天元青年基金资助项目（11326211）

通信地址：300387天津市西青区宾水西道399号天津工业大学计算机科学与软件学院

Address：School of Computer Science and Software Engineering，Tianjin Polytechnic University，399 Binshui Rd West，Xiqing District，

Tianjin 300387，P.R.China