前端调速式风电机组功率优化控制研究＊

张生睿，董海鹰

（兰州交通大学自动化与电气工程学院，甘肃兰州730070）

1 引言

随着风电产业的快速发展和逐渐成熟，风电机组的运行效率受到越来越多的关注和研究。在有效提高风电机组功率输出的同时保证输出功率的平滑性水平、提高风电质量、保证风电安全可靠并网已成为当前风力发电技术的研究重点。

目前以双馈型和直驱型机组为代表的变速恒频风电机组已成为风力发电技术的主流，针对此类风电机组的功率控制已有一定研究［1－5]。文献［1]基于微分跟踪器对双馈风电机组的功率曲线自寻优控制策略进行了研究；文献［2、3]提出了一种自适应增益调度线性二次型高斯最优控制策略，对变速恒频风电机组的运行优化问题进行了研究；文献［4]基于奇异摄动理论和逆系统方法对变速变桨距风机的水平功率控制进行了研究；文献［5]通过模态线性化过程建模被控对象，对风电机组的转矩控制、桨距控制及整机协调控制进行了研究。

以上文献从提高风电机组发电效率、稳定风轮转速、减轻传动链载荷、平滑输出功率、改善风电并网发电质量等不同方面进行了研究并取得了一定成果。

不同于传统后端稳频式风电机组，前端调速式风电机组采用无刷电励磁同步发电机发电，以液力变矩调速驱动取代传统的变频馈电模式，在同步发电机前端进行调速，有效解决了传统风电机组存在的低电压穿越能力差、无功输出能力不足等问题，为风电机组与电网直接耦合提供了条件［6]。

目前已经有相关文献针对此新型机组进行了研究［7－10]。文献［7]通过建立传动系统动态模型，对液力调速系统的速度调节特性进行了仿真研究；文献［8]对液力传动系统的结构参数优化进行了研究，并设计了相应的控制系统；文献［10]对液力传动装置主要参数及其对风力发电系统性能的影响规律进行了研究。以上文献主要针对液力变矩调速系统，从传动系统特性分析、结构参数优化及控制系统设计等不同方面进行了研究。

本文以前端调速式风电机组为对象，对其输出功率优化控制进行研究，采用差分进化算法对机组桨距角与导叶开度角两个控制参数进行优化，风电机组的变桨控制器与液力调速控制器根据优化后的参数进行控制，确保两个系统相互配合、协调工作，实现对风电机组输出功率的优化控制。

2 前端调速式风电机组

2.1 工作原理

传统的风电机组采用变频调速技术，通过变频器控制实现风机转速、频率和功率的调节。前端调速式风电机组采用无刷电励磁同步发电机（EESG）发电，通过液力变矩调速技术在EESG前端进行调速。风能由风轮输入，经过增速齿轮箱增速和液力变矩调速系统WinDrive将变化的风轮转速转化为EESG正常工作所需的恒定输入转速，最后通过EESG直接并入电网提供电能，其机组结构如图1所示。

图1 前端调速式风电机组结构图

2.2 变桨系统

根据空气动力学特性，风力机的风能捕获与风速v存在以下关系：

式中：Pm为风力机机械功率，S为风轮扫掠面积，ρ为空气密度，v为风速，λ为叶尖速比，β为桨距角。CP为风能利用系数，描述其变化的精确表达式目前还难以获得，为了研究需要，本文对CP进行近似处理，给出其近似表达式：

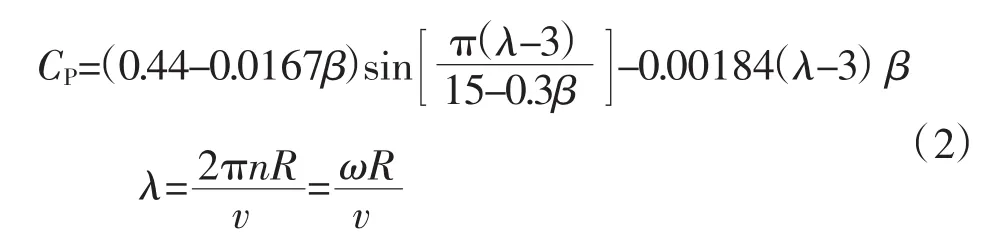
式中，ω为风力机主轴转速，R为风轮半径。风轮输出转矩Tm与风速v的关系式如下：

由式（2）分析可知：桨距角β一定时，风能利用系数CP存在唯一最大值；桨距角β为零时，风能利用系数CP最大；当β增大时，CP值逐渐减小。根据变桨距风力发电机的工作特性确定其不同运行状态下的变桨控制策略：在低于额定风速时，为了获得最大风能利用率，令β＝0，可最大程度捕获风能；在高于额定风速时，根据实时风速调节桨距角，使风电机组的输出功率保持在额定值附近。

2.3 液力变矩调速系统

从功率传递角度分析，由风轮输入的变速变转矩的功率，经过行星齿轮箱及液力变矩调速系统转换成恒转速变转矩的功率输出，直接作为EESG的输入功率，从而保证风电机组正常工作向电网输送有功功率。

液力变矩调速系统在变速输入与恒速输出的转换过程中起调节控制的作用，对其工作原理及特性进行分析可知，风轮转矩与液力变矩系统行星架转矩关系式如下：

液力变矩调速系统内部泵轮转矩与涡轮转矩关系式如下：

其中，TT为涡轮转矩；TP为泵轮转矩；D为液力变矩器油密度；μ为液力变矩器变矩比；λP为泵轮力矩系数。

变化的风轮转速，恒定的发电机输入转速，即涡轮输出转速与风轮转速之间的匹配关系为：

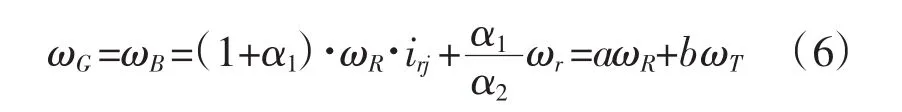
其中，ωG为发电机输入转速，ωB为泵轮输出转速，ωT为涡轮输出转速，irj为风轮到行星架的传动比，a和b为液力变矩调速系统的结构常数。式（6）为发电机正常工作时涡轮转速与风轮转速之间应保持的关系。风轮通过驱动行星架旋转，太阳轮驱动液力变矩器泵轮和发电机，涡轮驱动齿圈旋转，通过液力变矩器涡轮输出转速的调节，使齿圈转速响应风轮转速变化，从而达到发电机恒转速输入的目的。最后液力变矩器输出的转矩与同步发电机输入的转矩之间的关系式如下：

对以上各式进行分析：λP是关于iTB和导叶开度x的函数，iTB是关于风速v和ωP的函数，ωP是关于与风速v的函数。将式（4）、（5）代入式（6），则电励磁同步发电机的输入转矩可表示为关于风速v和导叶开度x的函数，如式（7）所示：

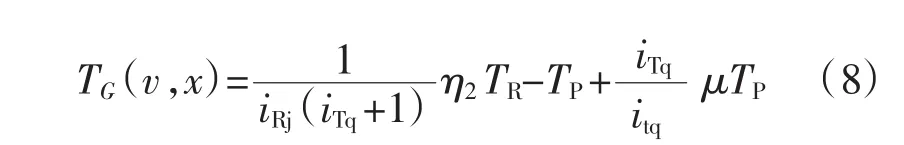
由液力变矩调速系统内部导叶调节机构分析，得到导叶开度角θ的表达式为：

以上各式的推导以及具体参数定义请参阅参考文献［7-10]。

针对液力变矩系统工作原理分析及相关参数的推导确定液力变矩调速系统的控制策略：在变风速情况下，通过导叶开度的调节，改变液力变矩器传动比，实现对涡轮转速的控制，液力变矩器输出的涡轮转速通过差动轮系与外齿圈相互作用，带动主轴转动，保证EESG输入保持在1500rpm的额定转速，即实现前端调速功能；同时通过对导叶开度的调节改变液流动量矩，进而改变涡轮的力矩，即实现变矩功能。综合以上分析，设计前端调速式风电机组有功功率控制结构框图如图2所示。

图2 风电机组有功功率控制结构框图

3 风电机组功率优化控制

3.1 优化控制策略

由于风能的不确定性以及风电机组本身的特性，风电并网输出有功功率波动较大，会对电网电能质量造成负面影响。因此有必要对风电机组输出功率进行控制，提高输出有功的平滑性，进而提高机组并网运行的稳定性。

本文针对额定风速以上前端调速式风电机组有功功率优化控制进行研究。功率优化控制方法采用分级递阶控制结构，将前端调速式风电系统分为两级，上级为功率优化控制系统，下级分为两个子系统，系统结构示意图如图3所示。

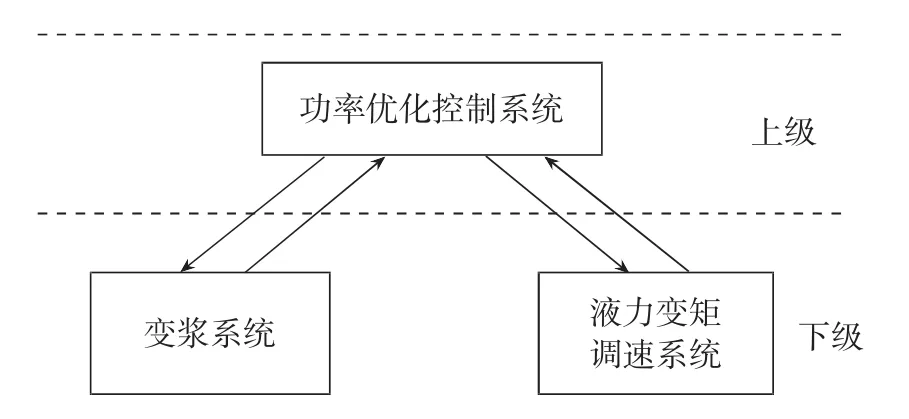
图3 系统结构示意图

3.2 目标函数

根据液力变矩调速系统输出转速稳定性与风电机组输出功率平滑性构建目标函数。使Wind－Drive的输出转速趋于稳定，机组输出功率平滑性趋于最优。建立风电系统参数优化数学模型如下：

式中，f01（β，θ）为液力变矩器输出转速的波动大小；f02（β，θ）为风电机组输出功率的波动大小，二者均取最小值，即满足液力变矩调速系统输出转速恒定，风电机组输出功率曲线平滑性最优。其表达式如下：

式中：ωref＝1500rpm，为同步发电机正常工作所需要的额定转速；ωG为液力变矩调速系统实际输出转速，由式（4）、（5）、（6）给出；Pref＝2000kW，为风电机组输出额定功率；PG为风电机组实际输出功率；v为输入变量；β与θ为待优化参数。

在功率优化控制系统中，根据所构建的目标函数，采用差分进化算法寻优，在给定约束条件下求解风电机组的最佳运行控制参数桨距角β和导叶开度角θ。一方面，变桨控制器根据优化后给出的桨距角控制执行机构动作，保证输出功率的平滑与稳定；另一方面，液力变矩控制器根据优化后给出的导叶开度进行转矩调节，进一步平滑机组的输出功率。

3.3 约束条件

（1）风电机组出力上下限约束

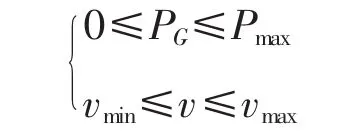
该约束保证机组持续输出有功，同时其上限应维持在额定值附近；对变量v要求其在额定风速12m／s以上，同时又不能超出机组切除风速25m／s，保证机组在正常工况下运行。

（2）桨距角与导叶开度角调节范围约束

该约束考虑变桨系统桨距角调节范围，β在0°至90°间变化；考虑变矩系统导叶调节范围，θ在0°至37°之间变化；也考虑限定待优化变量范围，以方便算法快速寻优。

（3）有功输出误差与转速输出误差约束

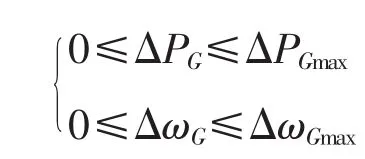
该约束考虑同步发电机输入转速要求，保证其稳定在额定转速值附近，且波动误差不超过5rpm；也考虑风电机组有功输出范围要求，波动误差不超过200kW。ΔPG与ΔωG分别为一个控制周期内机组输出有功与液力变矩调速系统输出转速的误差变化。

3.4 差分进化算法

差分进化算法（Differential Evolution Algorithm，DE）由Storn和Price于1995年提出，是一种基于实数编码的进化计算技术。最初设想用于解决切比雪夫多项式问题，后来发现DE算法也是解决复杂优化问题的有效技术。DE算法通过群体内个体间的合作与竞争产生的群体智能指导优化搜索。相比于传统进化算法保留了基于种群的全局搜索策略，采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性［11]。

在可行域内讨论研究minf（x）优化问题，假设初始种群为第 t代种群为种群规模为 N，变异常数为 F，交叉概率为 CR，变异后的中间个体为 ui（t），原目标个体与变异后中间个体随机交叉得到的中间个体为 Wi（t），则 DE 算法过程描述如下：

（1）初始化：在解空间内选择 X（0）作为初始种群，设置变异常数为F、交叉概率为CR、种群规模为N。为保证初始种群内每个个体都是优化问题的可能解，初始化种群使之在给定范围内进行随机取值。

（2）变异：随机选择 r1，r2，r3∈rand（1，n），且 i≠r1≠r2≠r3，则：

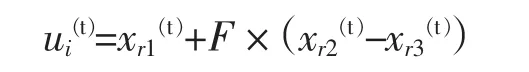
其中 N≥4，变异算子 F∈［0，2] ，是一个实常数因数，控制偏差变量的放大。

（3）交叉：

（4）选择：

本文所建立的功率优化模型为多约束非线性模型，对该模型的求解为多目标优化求解。本文采用将子代个体和父代个体进行选择操作后获得混合种群的多目标差分进化（Differential Evolution for Multi-objective Optimization，DEMO）。DEMO 中采用与标准差分进化算法一致的种群初始化、选择、交叉操作。不同点在于，针对多目标求解问题，在个体进行选择操作时，引入Pareto支配概念。按照子代个体与父代个体的目标适应值，确定进入临时种群P的个体。对经过选择操作后的临时种群，为维持种群规模，对其进行基于快速支配排序和拥挤度计算的阶段操作，从而确定进入下一代的个体。

差分进化算法运行参数少，但每个参数对算法的求解效率和优化结果有很大影响。变异因子F控制差分向量的变异程度，影响优化求解的收敛速度。交叉概率CR影响种群多样性，避免算法陷入局部最优解。本文对参数选择采取动态调整策略［12]。在进化初期选择较小的变异因子与交叉概率，保证算法稳定性；进化后期选择较大的变异因子与交叉概率，提高优化求解的收敛速度。

在本文所设计的功率优化控制器中，采用DEMO对两个目标函数进行优化。开始随机生成种群P，种群规模为N。对种群进行非支配排序，每对解的适应度就是它的非支配水平。进行选择、交叉和变异，生成子代种群Q，进入DEMO循环，最后得到Pareto解集，对解集中的解加权平均作为目标优化的最优解。

4 仿真与分析

4.1 算法实例

本文在前端调速式风电机组实际运行数据基础上，运用MATLAB语言编写优化算法程序并生成m文件。取额定风速v＝11m／s工况下进行优化。风电机组基本参数如表1所示。

表1 风电机组参数表

算法基本参数设置如下：初始种群大小N＝50，最优前端个体系数为 0.4，变异因子 Fmax＝0.7、Fmin＝0.3，交叉概率 CRmax＝0.8，CRmin＝0.2，最大迭代次数tmax＝200，适应度函数偏差值为 0.1。

在DEMO优化运行过程中，自动绘制出第一前端中个体的分布情况，个体分布随着算法进化一代而更新一次。当满足最大迭代次数迭代停止后，得到如图4所示的第一前端个体分布图。

图4 第一前端个体分布图

由图4可以看出，第一前端的Pareto最优解分布均匀，同时，在Workspace中返回本次运行所得到的Pareto最优解如表2所示。

表2 算法运行所得Pareto最优解

从表2可以看出，返回的Pareto最优解个数为20个，对比算法初始种群大小50，最优前端个体系数0.4的设置发挥了作用，同时可以看出个体被限制在［0，37] 、［0，90] 的范围内。由于算法初始种群随机产生，因此每次运行的结果不一样，但是可以保证算法每次优化所得的解是满足目标函数的最优解。

4.2 整机运行仿真与分析

在Simulink环境下搭建前端调速式风电机组整机运行仿真模型。所编写的参数优化程序通过自定义S函数实现与仿真模型的连接，如图5所示。

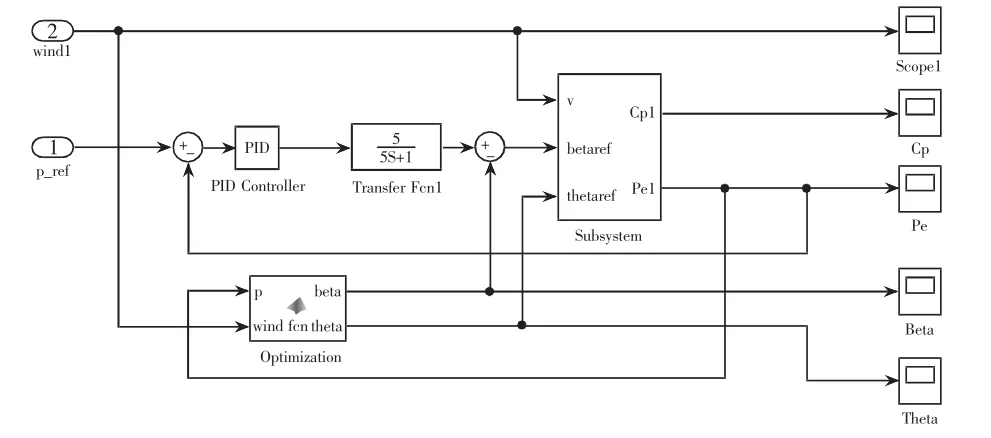
图5 风电机组功率优化控制仿真模型图

以10秒为时长进行仿真，运行结果如图6-图10所示。

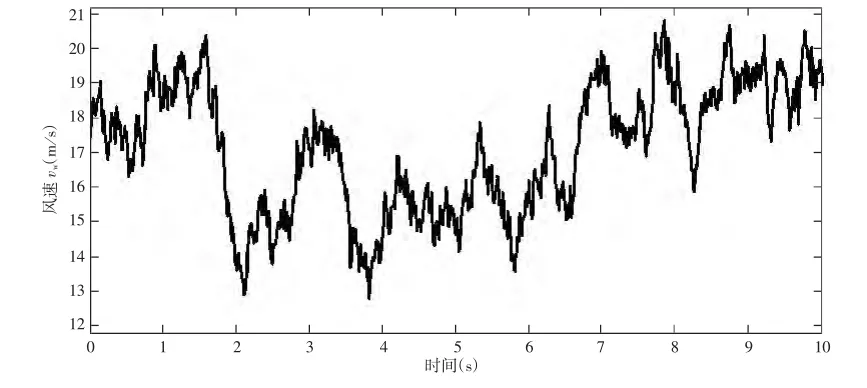
图6 风速曲线图

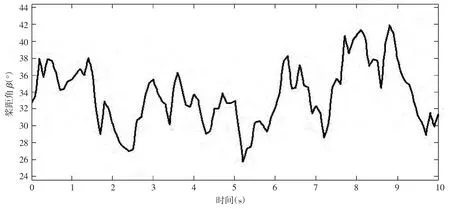
图7 桨距角变化曲线图

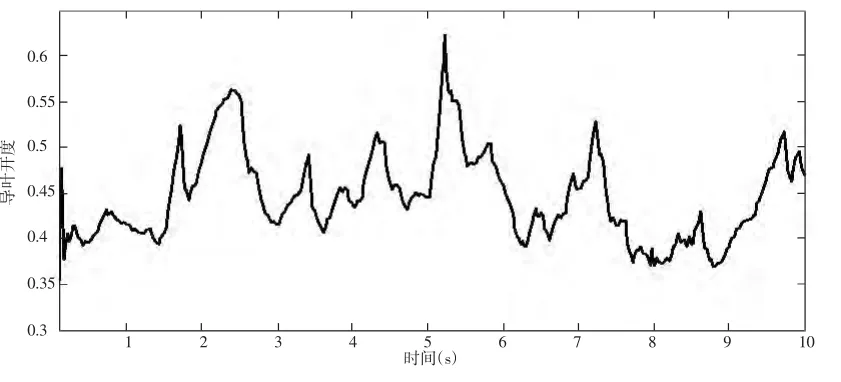
图8 导叶开度变化曲线图

图9 桨距角曲线对比图

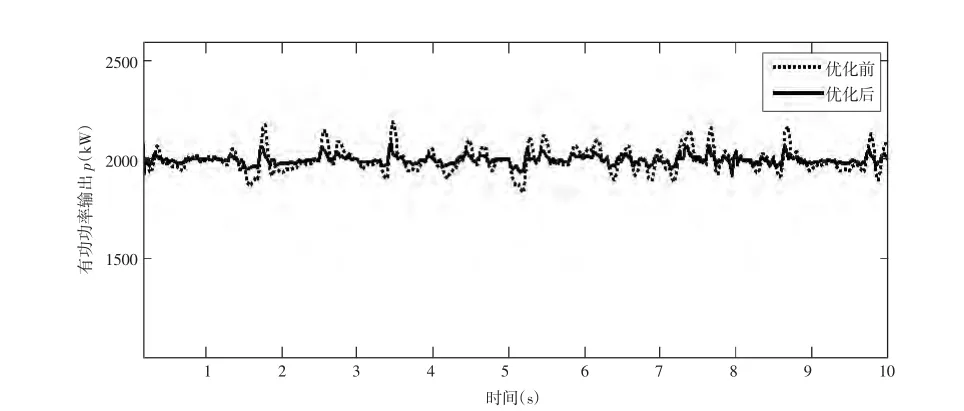
图10 机组输出功率曲线对比图

图6所示为仿真所用的风速样本。图7所示为优化控制模块根据实时风速优化后给出的变桨系统桨距角变化曲线图。可以看出桨距角随风速变化，风速较大时，桨距角增大，风速较小时，桨距角减小，其变化趋势与理论分析情况相符合。变桨系统根据优化给出的桨距角进行控制，在高风速情况下限制风能吸收，保证机组输出功率稳定在额定值附近。

图8所示为优化所得液力变矩调速系统的导叶开度变化曲线。导叶开度随风速在0.3－0.6范围内变化，对应的导叶开度角在 11.1°－22.2°范围内变化，液力调速系统根据优化后所提供的导叶开度进行控制，一方面实现液力调速系统1500rpm额定输出转速的调节，作为同步发电机的输入转速保证其正常工作；另一方面液力变矩器根据导叶开度对涡轮输出转矩进行调节，进而对同步电机主轴转矩进行控制，实现了机组输出功率的平滑性调节。

图9所示为优化前后机组桨距角的变化曲线对比图。从趋势上看，优化后桨距角变化与实际运行情况保持一致。从数值上看，通过参数优化控制模块直接求解提供精确桨距角给变桨系统进行控制调节，减小了变桨系统动作频率，减轻了风轮处的振动及由此引起的部分载荷。

图10所示是将加入优化算法前后的风机模型联合仿真得出的机组输出功率曲线对比图。从图中可以看出，机组的输出功率随风速变化，优化前机组输出功率波动较大，且瞬时幅值最高为300kW，优化后功率波动较小，瞬时幅值最高为100kW，输出有功的平滑性有了明显提高。

5 结束语

本文针对新型前端调速式风电机组有功功率控制进行研究，从参数优化角度出发，提出了基于差分进化算法的风电机组功率优化控制策略，编写优化算法程序，通过自定义模块与前端调速式风电机组模型连接运行，求解得出符合当前工况的最优桨距角和导叶开度角，机组控制系统以此为参考分别对变桨与液力变矩系统调速系统进行控制。仿真结果表明优化后的控制策略明显抑制了发电机的功率波动，保证了机组输出功率的平滑性，也验证了该控制方法的有效性和可行性。

［1] 夏安俊，徐浩，胡书举，许洪华.大型风电机组的功率曲线自寻优控制策略［J] .高电压技术，2012，（8）：2023－2029.

［2] 白焰，范晓旭，吕跃刚，徐大平，杨锡运.大型风力发电机组动态最优控制策略研究［J] .电力系统自动化，2010，（12）：90－94.

［3] 范晓旭，白焰，吕跃刚，徐大平.大型风力发电机组线性二次型高斯最优控制策略［J] .中国电机工程学报，2010，（20）：100－105.

［4] 耿华，杨耕.变速变桨距风电系统的功率水平控制［J] .中国电机工程学报，2008，（25）：130－137.

［5] 姚兴佳，邢作霞，刘颖明，王晓东.变速变距风力发电机组整机协调控制策略研究［J] .太阳能学报，2009，（5）：639－644.

［6] A unique solution to generating electricity from the wind WinDrive technology［R] .Voith Turbo Wind，2008.

［7] 李成武.大功率风电机组新型传动系统建模与仿真研究［D] .重庆：重庆大学，2007.20－26.

［8] 刘彬.风力发电液力调速系统及其控制研究［D] .长春：吉林大学，2012.29－35.

［9] 马文星，刘彬，刘春宝等.风力发电液力调速系统及其控制［J] .吉林大学学报（工学版），2013，43（5）：1276－1283.

［10] 闫国军，董泳.风力发电液力机械传动装置的特性及设计［J] .太阳能学报，2012，（4）：571－576.

［11] 刘波，王凌，金以慧.差分进化算法研究进展［J] .控制与决策，2007，（7）：721－729.

［12] 彭春华，相龙阳，刘刚，易洪京.基于支持向量机和微分进化算法的风电机优化运行［J] .电网技术，2012，（4）：57－62.

［13] Voith WinDrive for large converterless wind turbines［R] .China Wind Power Information.2011.

［14] H.Muller，M.P.ller，A.Basteck，et al.Grid－com－patibility of variable speed wind turbines with directly coupled synchronous generator and hydro－dynamically controlled gearbox［A] .In large－scale integration of wind power and transmission networks for offshore wind farms.The 6th International Workshop［C] .Delft：LSIWPTNOWF，2006.307－315.

［15] Soliman，M.Malik，O.P.Westwick，D.T.Multiple model pedictive control for wind turbines with doubly fed induction generators［J] .IEEE Transactions on Sustainable Energy，2011，2（3）：215－225.

［16] （罗）蒙特安努.风力发电系统优化控制［M] .北京：机械工业出版社，2010.

［17] 姚兴佳，宋俊.风力发电机组原理与应用［M] .北京：机械工业出版社，2009.