移动荷载作用下长大纵坡饱和沥青路面的水力耦合分析

王海峰，但汉成，滕旭秋（.宁夏公路建设管理局，宁夏 银川 750000；.中南大学 土木工程学院，湖南 长沙 40075；.兰州交通大学，甘肃 兰州 70070）

移动荷载作用下长大纵坡饱和沥青路面的水力耦合分析

王海峰1，但汉成2，滕旭秋3
（1.宁夏公路建设管理局，宁夏 银川 750000；2.中南大学 土木工程学院，湖南 长沙 410075；3.兰州交通大学，甘肃 兰州 730070）

为了解长大纵坡饱和沥青路面的水损害机理，基于Biot固结理论和多雨地区长大纵坡的特点，建立了在移动荷载作用下长大纵坡饱和沥青路面“面层-基层-路基”二维三层体系水力耦合模型和水力耦合控制方程，在面层底部为完全排水边界条件下全面系统地分析了车辆荷载、荷载移动速度和纵坡坡度对面层中正应力、孔隙水压力、剪应力和面层位移等物理量分布的影响，为长大纵坡沥青路面结构设计提供理论基础和参考。结果表明：车辆荷载和荷载移动速度对面层中正应力、孔隙水压力、剪应力和面层位移产生显著影响，而纵坡坡度对面层中正应力、孔隙水压力、剪应力和面层位移几乎不产生影响。

长大纵坡；饱和沥青路面；移动荷载；水力耦合；路面结构设计

0　引言

目前，长大纵坡沥青路面水损坏被认为是最常见的一种路面早期破坏行为，但其损害机理到现在为止还不明确。在出现了这种损害之后，研究者们通常都是通过室内试验模拟或者从化学和物理方面研究静水作用下沥青膜是怎样剥落的[1]，但对超载、车速、坡度对路面内孔隙水压力、正应力、剪应力和位移产生何种影响等一系列问题研究得还不够深入。为了阐述水对路面的破坏机理，Khalili等从不同角度、采用不同方法研究了动载荷和水的耦合作用下路面各种物理场的分布情况，傅搏峰等[2]以Biot固结固结理论、疲劳损伤力学原理和各向同性线弹性损伤理论为基础，建立了沥青路面水损害的力学分析模型。学者们虽然对水损坏是如何发展以及水对路面的作用进行过一些研究和总结，但事实上都是从经验出发，缺乏理论方面的定量研究。因此，本文提出了长大纵坡饱和沥青路面的数值计算模型，综合考虑在行车荷载、水以及坡度的共同作用下路面的受力情况，从理论上研究了长大纵坡水损坏的破坏机理，然后尽可能提出有效的防治措施，具有一定的理论指导和工程意义[3]。

1　水力耦合模型及动态响应控制方程

1.1水力耦合模型

选取长大纵坡路面的一部分作为研究对象，建立一个以x轴为路面横向、z轴为路面深度方向，包含面层、基层和路基的二维模型。把纵坡路段面层视为饱和的弹性多孔介质，面层厚度为H1，把纵坡路段基层和路基视为干燥的弹性介质，基层厚度为H2，路基的厚度为H3。现假定路基在某一深度处的位移为0，或者路基在某一深度处固定于刚性路床上，将面层、基层和路基的横向宽度视为无限大，纵坡路段面层内的水在车辆荷载作用下可以自由溢出顶面。本文考虑了纵坡路段面层处于最不利条件下的水损害情况，即面层孔隙都处于饱水状态[3-4]，二维模型如图1所示。

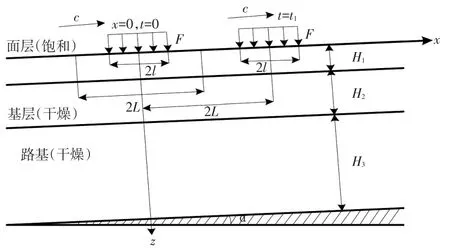
图1　水力耦合模型示意图

根据长大纵坡饱和沥青路面的状况，基于Mat⁃lab编程计算，建立了能够分析纵坡段沥青路面水损坏的简化模型。为了方便建立模型，还需做如下假设[5-6]：

①路面各结构层为均质的各向同性的弹性材料；

②在荷载作用下面层材料会产生变形，但假定渗透系数保持不变；

③仍然可以采用达西定律描述液相的动量；

④固相和液相的体积应力不计；

⑤各结构层间位移和应力连续；

⑥孔隙水和沥青混凝土均不可压缩，即只有变形，没有体积变化；

⑦不考虑水平荷载的作用。

长大纵坡沥青路面面层由沥青和集料组成，沥青和集料具有孔隙，水填充于孔隙中。假设液相运动的平均速度为n（nx和nz），固相运动的平均速度为w（wx和wz），液相的密度为ρf，固相的密度为ρs，孔隙率为n。根据Biot动力固结理论，有如下控制方程[7]：

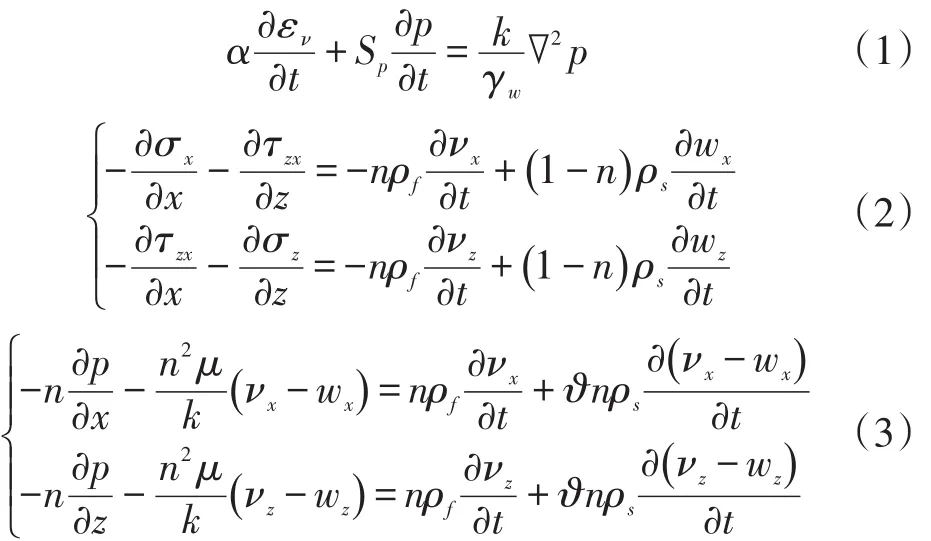
式（1）~式（3）中：Cm为多孔介质压缩系数（Pa-1）；Cs为固相材料的压缩系数（Pa-1）；a为Biot固结系数，a=1-Cs/CM；Sp为孔隙的弹性释水系数（Pa-1），表示为Sp=nCf+(a-n)Cs；Cf为液相（水）的压缩系数；ev为体积应变；k为渗透系数（m/s）；sx、sz、tzx为固相在x、z面上的正应力（Pa）和剪切应力（Pa）；p为孔隙水压力（Pa）；k为渗透率（m2）；ϑ为孔隙分布的曲率系数；m为孔隙水的动力黏滞系数（Pa·s）；gw为水的容重（kg·m-2·s-2）；t为时间坐标；∇2为Laplace算子。

式（1）为由质量守恒定律得到的连续性方程，式（2）为液相与固相共同作用下的动量方程，式（3）为液相的动量方程。

根据本文模型的第③条假设，可以将式（3）等号右边整体化为0；对于二维平面应变问题，依据Hooke应力应变原理以及材料的阻尼特性，由上述质量守恒定律控制方程（式（1））、液相与固相动量控制方程（式（2））和液相动量方程（式（3））可以得到面层、基层和路基动态响应控制方程。

面层渗流模型的动态响应控制方程为：

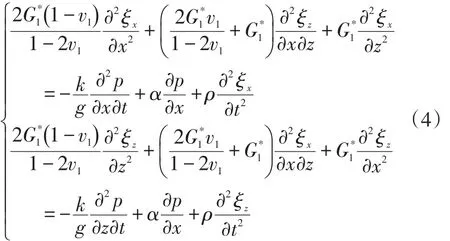
根据对面层系统的研究，同样，基层和路基也可以采用动力平衡方程来描述。

基层模型的动态响应控制方程为：

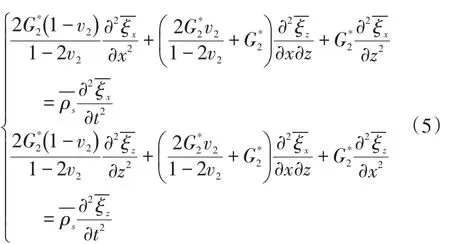
路基模型的动态响应控制方程为：

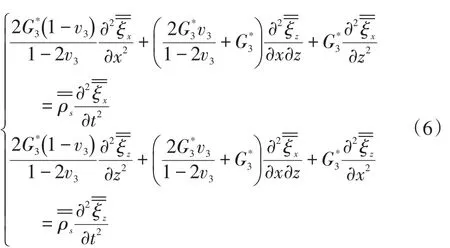
G*为复弹性剪切模量，可以表示为：

式中：d为材料阻尼系数；G为固相在静止状态下的剪切模量（Pa）；i为复数，i=。

1.2面层、基层和路基模型的动态响应控制方程通解

1.2.1移动交通荷载表达式

在二维情况下，可以将交通荷载简化为条形荷载。荷载宽度为2l，强度为F，以速度c移动。作用于路面的荷载采用Fourier级数展开。假设从第一次荷载作用到下一次荷载作用的距离为2L（如图1所示），这个长度可以看作是两个交通荷载之间的距离，移动荷载函数（t=0）可以表示如下[8-10]：

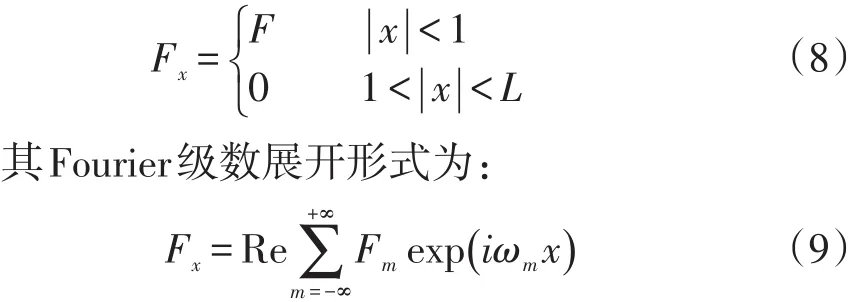
式中：Re表示取实部值，Fm和ωm均为只与m有关的函数，ωm=2πmT；T为移动荷载的分布周期，文中设为2L；m为实数，范围为-∞到+∞。

如果采用移动坐标体系，即假设坐标体系的移动速度和移动方向与荷载的移动速和方向相同，那么移动荷载在任意时刻t的Fourier级数表达式如下：

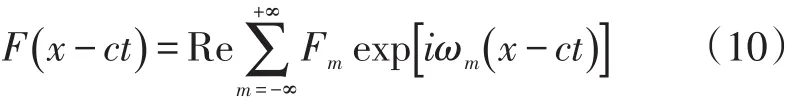
根据Fourier变换和坡度，作用于纵坡路面的Fm可以表示为：

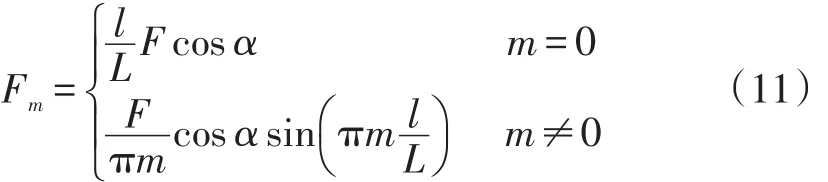
式中：a为坡面的夹角。

1.2.2控制方程的求解

由于面层的性质是独立于坐标系统的（各向同性），线性系统中的任何函数f(x,z,t)都可以表示为一组线性的谐函数的级数和[8]，其表示形式如下：

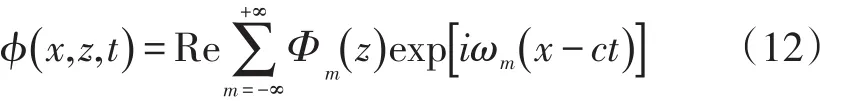
式中：Fm(z)仅为独立变量z的函数，Fm(z)=Fm为m次谐函数，指数函数部分仅为x-ct的函数。

根据式（12），面层控制方程可以表示为：

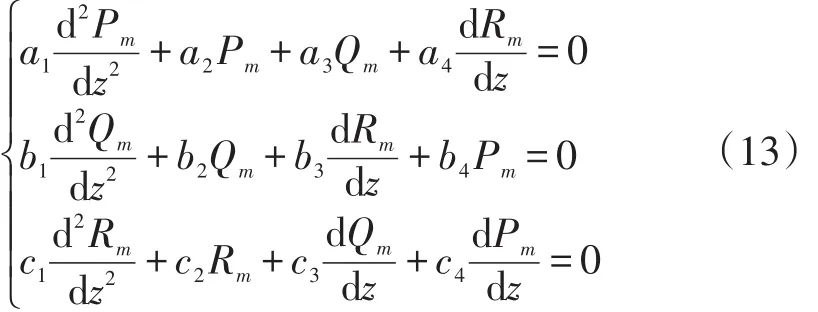
式（12）中的参数分别为：

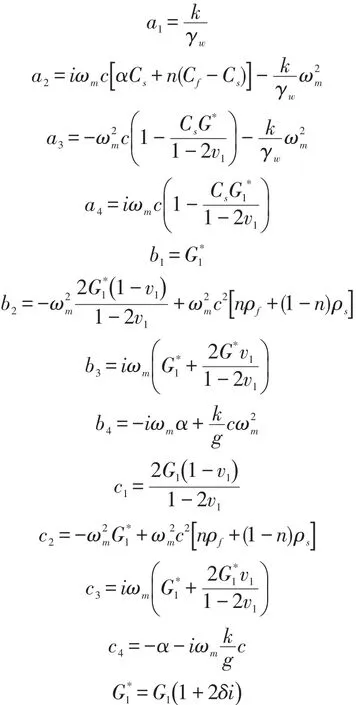
式中：G1为面层材料的剪切模量（Pa）；v1为面层材料泊松比。

因此，式（13）的通解可以表示为：

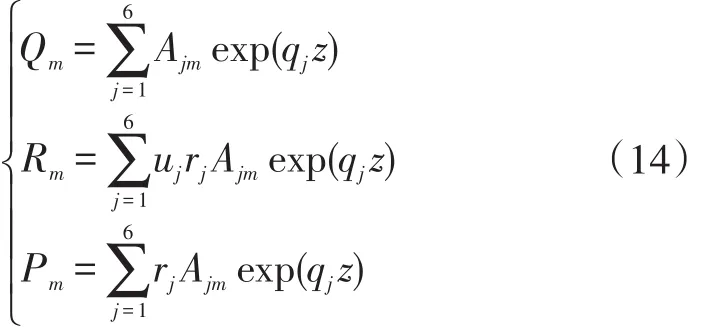
将式（14）代入到式（13）后简化得到：

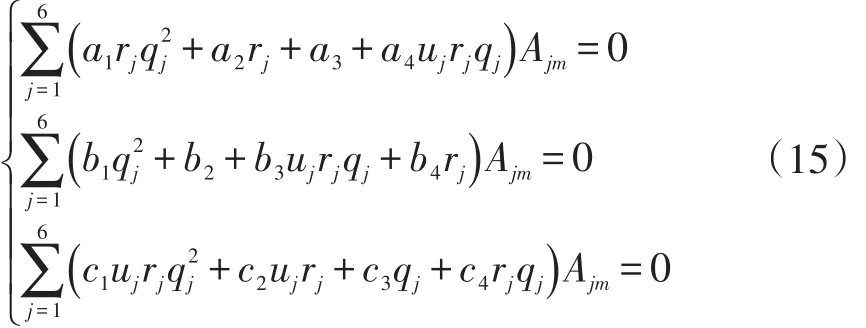
其中：

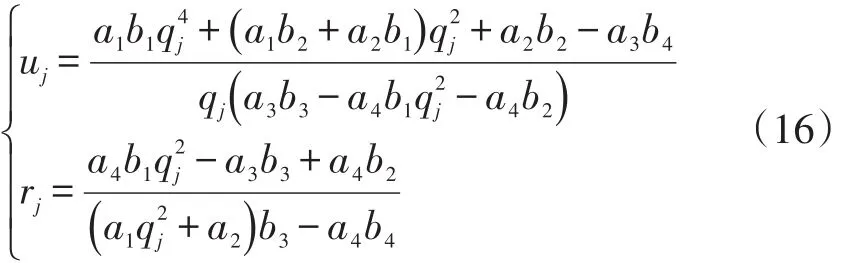
qj=(1，2，…，6)为以下六阶多项式（式（17））的解：

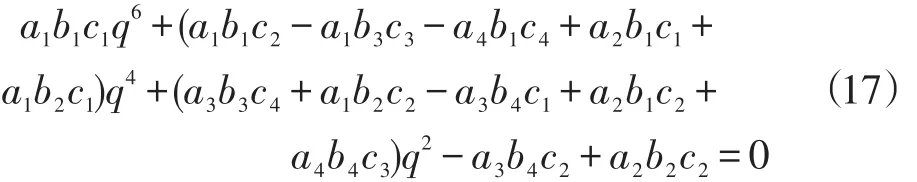
同理可得基层动态响应控制方程通解：

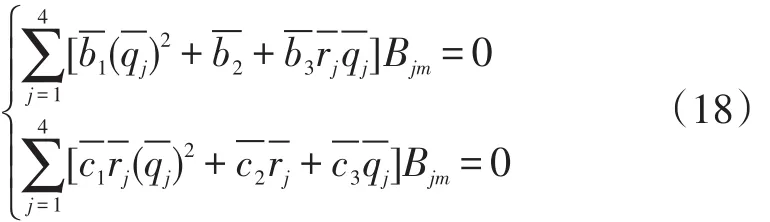
四阶多项式根，这个四阶多项式为：

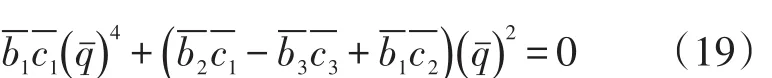
式（19）中的参数表示为：

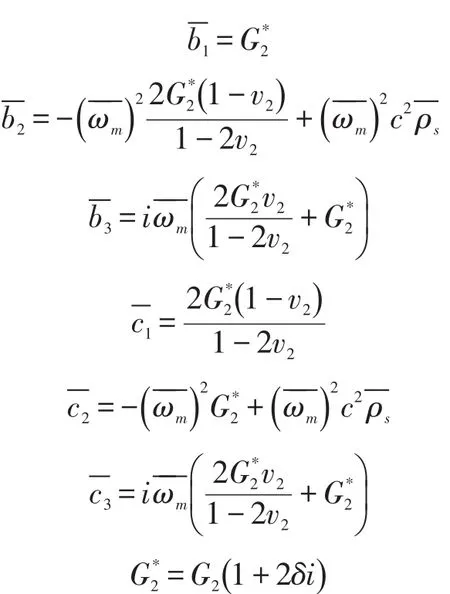
式中：G2为基层材料的剪切模量（Pa）；v2为基层材料泊松比。

路基动态响应控制方程通解为：

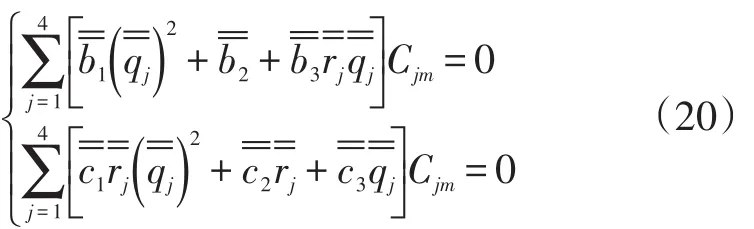
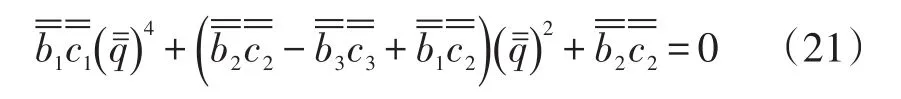
式中的参数表示为：

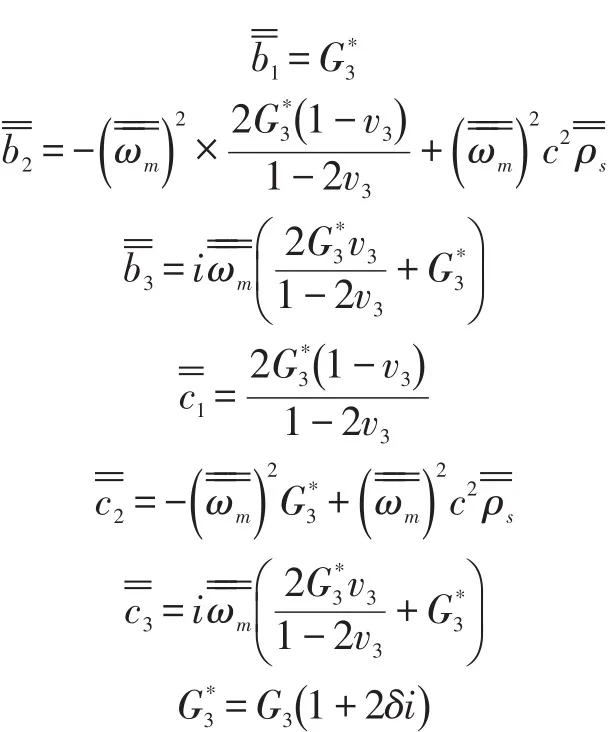
式中：G3为路基材料的剪切模量（Pa）；v3为路基材料泊松比。

1.3边界条件

要得到控制方程的解，就必须计算出积分常数，即Ajm(j=1,2,3,4,5,6)、Bjm(j=1,2,3,4)和Cjm(j= 1,2,3,4)，Ajm、Bjm及Cjm表示矩阵。由于车轮与沥青路面之间的摩擦为滚动摩擦，滚动摩擦力与长大纵坡路面上的车辆荷载相比，数量级特别小，所以车轮与路面产生的摩擦力的大小忽略不计。为了使得求解控制方程简易化，假设车轮与面层的剪切应力为0。综上所述，得到下面的边界条件：在面层顶面，即z=0处，剪应力txz=0，z方向正应力σz= F，孔隙水压力p=0；在面层底部的位移边界条件，即z=H1处，x方向的位移xx=d1，z方向的位移xz=δ2；同时在面层底部，为完全排水边界（p=0），即只考虑完全排水边界，不考虑不排水边界。就基层和路基模型而言，根据前文的连续性假设，可得到对应的边界条件，这里不再罗列[11]。

1.4位移、孔隙水压力、剪应力和正应力的表达式

根据面层、基层和路基的边界条件，利用Mat⁃lab编程计算可得位移、应力，然后代入路面系统动态响应控制方程的通解中，就可得到位移ξx、孔隙水压力p、剪应力txz和正应力σx的表达式：

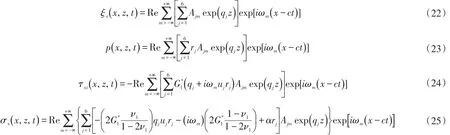
2　数值计算与分析

本文选择的荷载表达式为Fourier级数展开式，荷载函数为4 048个谐函数的级数和，轮胎与路面的接触压力为标准轴载下的荷载F（标准情况下接触压力为0.701 3MPa）。此外，还考虑了其他超载情况。纵坡坡度选取了0、2%、4%和6%四种情况，荷载移动速度c也采用了四种作计算对比：20m/s、40m/s、60m/s和80m/s。其他参数为：l=0.1m（轮胎与底面接触的单宽为0.2m），L= 50m（荷载间距为100m），H1=0.2m，δ=5%（多孔介质材料阻尼系数）[5]。沿着水平方向（xt=x-ct为变量）[12]，如果以xt作为参考坐标的话，动力响应可视为稳态分析，时间这一概念将被xt所替代，这样就将抽象的时间概念转变为具体位移形式，此时将z=0.1m（可设z等于其他深度值）处作为计算观察断面，其他参数见表1和表2[5]。

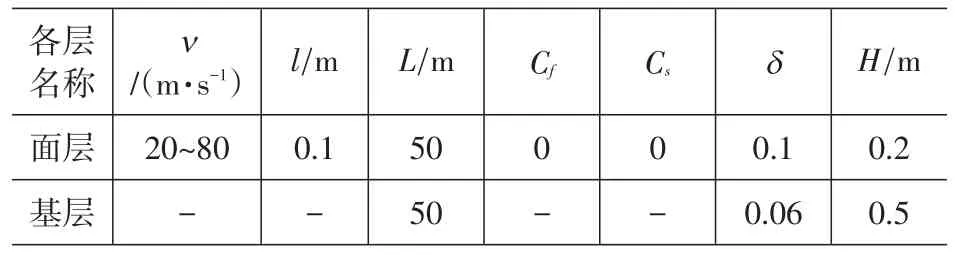
表1　与交通荷载和路面材料有关的参数

表1（续）

2.1车辆荷载的影响

本节将分别研究标准轴载和超载率为20%、40%、60%和80%五种情况，选取路面纵向坡度为4%，渗透系数k=10-6m/s，荷载移动速度c=40m/s，研究在不同荷载作用下路面正应力、孔隙水压力、剪应力和水平位移沿着路面横向的变化规律，计算结果如图2~图5所示。

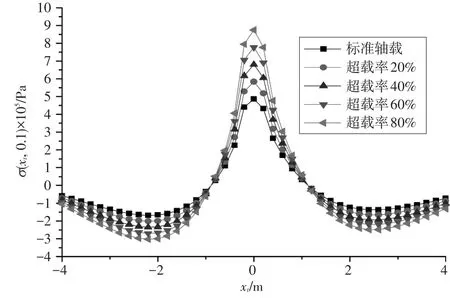
图2　不同轴载下正应力沿着水平方向的变化规律

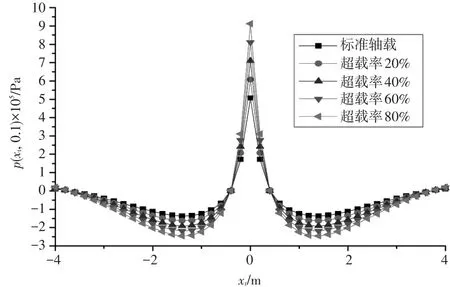
图3　不同轴载下孔隙水压力沿着水平方向的变化规律

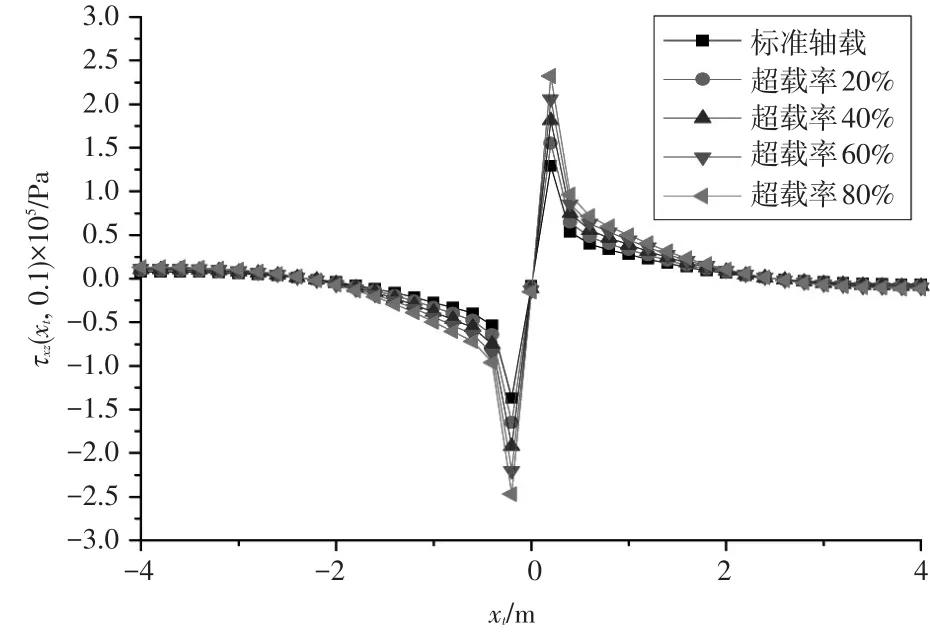
图4　不同轴载下剪应力沿着水平方向的变化规律

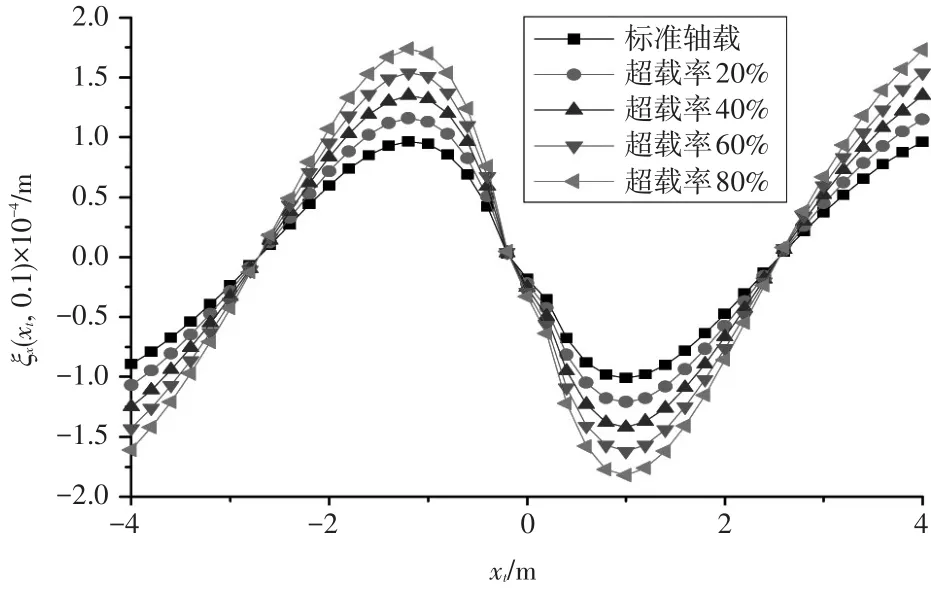
图5　不同轴载下水平位移沿着水平方向的变化规律

从图2可以看出，无论是标准轴载还是超载的情况，面层正应力沿着路面水平方向的分布特点相同，都是关于原点对称，正应力在荷载接近观察断面大约xt=±1m处出现剧烈变化，在较远处变化比较平缓，并在xt=0处达到了最大值，且其峰值为正值（面层受拉），即拉应力区集中出现在面层荷载作用中心处；当荷载由标准轴载100kN增大到120kN、140kN、160kN和180kN时，最大正应力分别增加了19.9%、39.9%、59.9%和79.8%，说明超载情况下的正应力大于标准轴载下的正应力。由此可以看出，超载对正应力的影响非常显著，是不可忽视的因素之一。

从图3可以看出，同水平正应力一样，孔隙水压力也在xt=±1m时出现剧烈变化，在较远处变化比较平缓，孔隙水压力在xt=0处达到最大值，孔隙水压力沿水平方向先衰减后增大；当车辆荷载由标准轴载100kN增大到180kN时，最大孔隙水压力由5.07×105Pa增大到9.12×105Pa，这就说明超载情况下孔隙水压力要大于标准轴载下的孔隙水压力，车辆超载情况越严重，面层内产生的孔隙水压力也就越大。因此，在长大纵坡路段，为防止路面过早破坏，就要严格限制车辆超载。

从图4可以看出，当荷载移动距离xt为1～4m时，剪应力迅速减小，最后趋于0；当荷载移动距离xt为0～1m时，剪应力先增大后减小，在xt=0时剪应力等于0；在荷载边缘（xt=±0.1m）处，面层中的剪切应力达到最大值，方向相反。整体来看，剪应力沿观察面水平方向变化响应程度不一致，超载下的剪应力要大于标准轴载下的剪应力。当车辆荷载由标准轴载100kN增大到180kN时，剪应力由1.29×10-5Pa增大到2.32×10-5Pa。

从图5可以看出，当荷载移动距离xt为1～4m时，水平位移随水平方向长度增大而增大；当荷载移动距离xt为0～1m时，水平位移随水平方向长度增大而减小；当荷载移动距离xt=0时，水平位移为0。由此可知，荷载在移动过程中，面层水平位移随水平方向长度变化的响应不一致，越接近观察面，这种变化幅度就越大；同时，随着车辆荷载的增大，水平位移也相应增大。

2.2荷载移动速度的影响

本小节研究在荷载移动速度c为20m/s、40m/s、60m/s和80m/s四种情况下，选取路面纵向坡度为4%，面层渗透系数k=10-6m/s，轴载为静载作用下的标准轴载BZZ-100（荷载压力为0.701 3MPa），研究在不同荷载移动速度下路面的正应力、剪应力水平位移和孔隙水压力沿着路面横向的变化规律，计算结果如图6~图9所示。

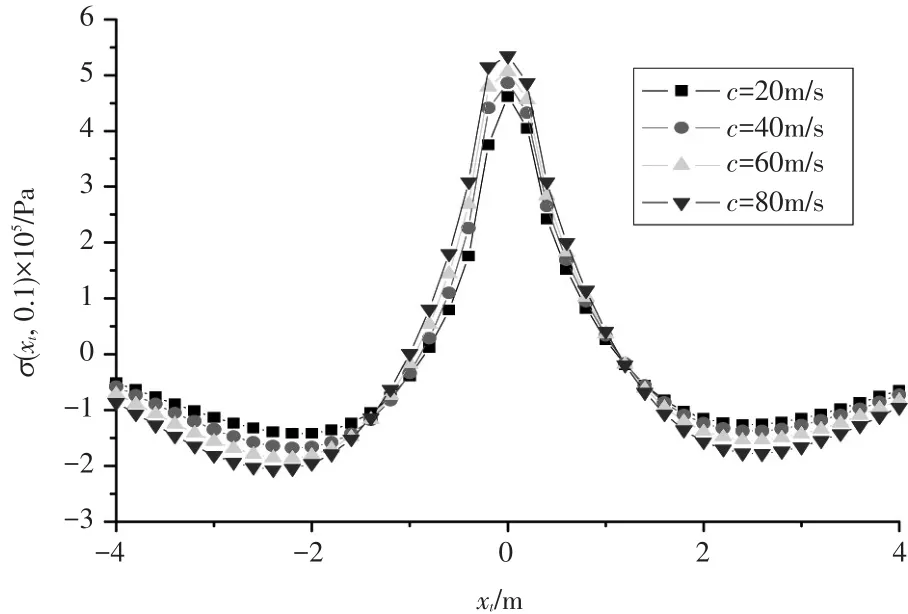
图6　不同移动荷载速度下正应力沿着水平方向的变化规律

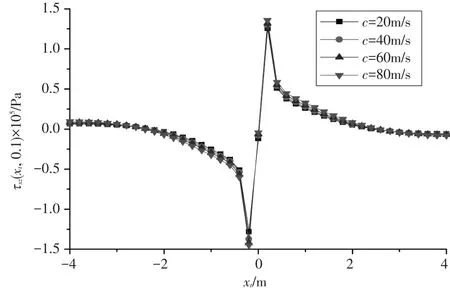
图7　不同移动荷载速度下剪应力沿着水平方向的变化规律

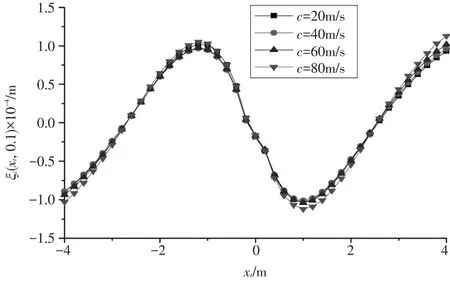
图8　不同移动荷载速度下水平位移沿着水平方向的变化规律

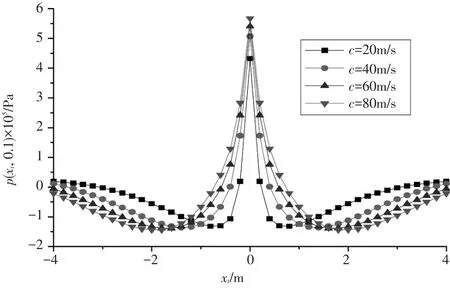
图9　不同移动荷载速度下孔隙水压力沿着水平方向的变化规律

从图6可以看出，正应力在xt为-1～1m处出现剧烈变化，在较远处变化相对较平缓，并且在xt=0处达到最大值，且其峰值为正值（面层受拉），即拉应力区集中出现在面层荷载作用中心处。整体来看，正应力沿水平方向先减小后增大；当荷载移动速度由20m/s增大到40m/s、60m/s和80m/s时，最大正应力分别增大了5.4%、9.8%和16.0%和79.8，说明移动荷载速度越大，正应力就越大。由此可以看出，移动荷载速度对正应力的影响非常显著，是不可忽视的因素之一。

从图7可以看出，当荷载移动距离xt为1～4m时，剪应力迅速减小，最后趋于0；当荷载移动距离xt为0～1m时，剪应力先增大后减小，xt=0时剪应力等于0；在荷载边缘（xt=±0.lm）处，面层中的剪切应力达到最大值，剪应力方向相反，而且剪应力的变化趋势沿观察面变化响应不一致。当荷载移动速度由c=20m/s增大到c=80m/s时，沿着x轴正方向，面层最大剪应力由0.125MPa增大到0.136MPa，可见荷载移动速度对水平方向的剪应力影响不明显。

从图8可以看出，当荷载移动距离xt为1～4m时，水平位移随水平方向长度增大而增加；当荷载移动距离xt为0～1m时，水平位移随着水平长度的增大而减小；当荷载移动距离xt=0时，水平位移为0；荷载移动至离开观察面后，这种变化趋势相反。由此可知，荷载在移动过程中，越接近观察面，这种变化幅度就越大。整体来看，荷载移动速度对水平位移的影响不是太明显。但也可以看出，荷载移动速度越快，面层水平位移也就相对越大。因此，荷载移动速度对路面的影响也是很重要的，如果长大纵坡上车辆行驶速度太慢，产生的水平位移就会使得路面出现推移和拥抱。

从图9可以看出，孔隙水压力沿着水平方向先减小后增大，在面层底部，孔隙水压力接近于0，正的最大孔隙水压力出现在荷载作用中心（xt=0）处，负的最大孔隙水压力产生的位置随着荷载移动速度的增大逐渐向观察面移动；当荷载移动速度由20m/s增大到80m/s时，最大孔隙水压力由4.31×10-5Pa增大到5.67×10-5Pa，孔隙水压力随着荷载移动速度的增加而增加。当荷载速度较小（c=20m/s）时，荷载驶向观察面时孔隙水压力沿水平方向上升，在xt=±1m处，急剧上升达到最大值；而当荷载移动速度为80m/s时，孔隙水压力沿水平方向上升，在xt=±2m处，急剧上升达到最大值。这就说明，当荷载以不同的速度移动过程中，路面内孔隙水压力沿着路面水平方向的响应程度是不一样的，越接近面层顶面和面层底面，荷载移动速度越大，产生的孔隙水压力就越大。

2.3纵坡坡度的影响

现假设行驶在长大纵坡沥青路面上的车辆车轮重力为25kN，静载作用下的标准轴载为BZZ-100（荷载压力为0.701 3MPa），车辆荷载移动的速度c= 40m/s，面层渗透系数k=10-6m/s。现取沥青路面的纵坡坡度分别为0、2%、4%、6%（如表3所示），研究在不同的纵坡坡度下路面的正应力、剪应力、孔隙水压力和水平位移沿着路面横向的变化规律，计算结果如图10~图13所示。

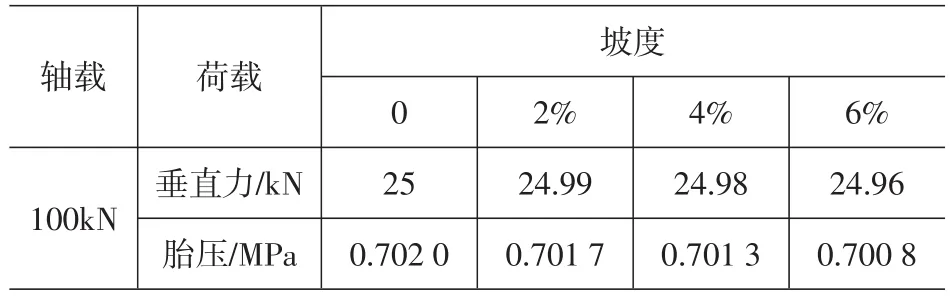
表3　标准轴载随路面坡度的变化

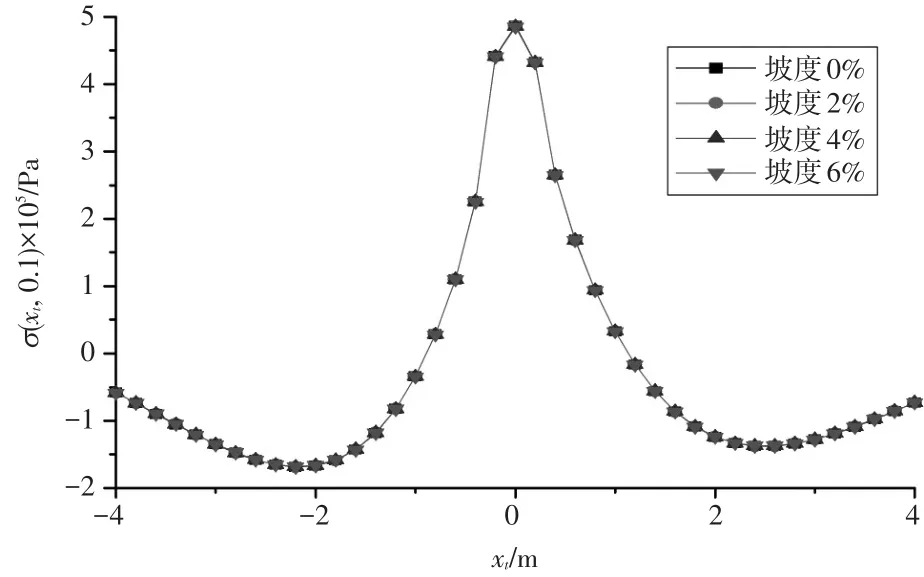
图10　不同坡度下正应力沿着水平方向的变化规律

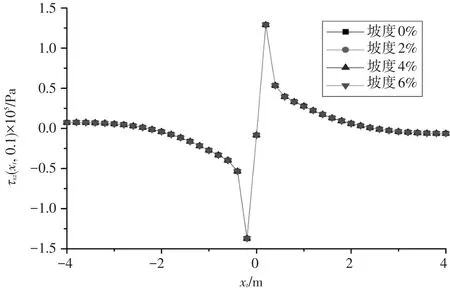
图11　不同坡度下剪应力沿着水平方向的变化规律

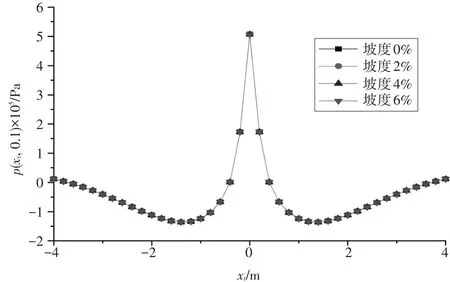
图12　不同坡度下孔隙水压力沿着水平方向的变化规律

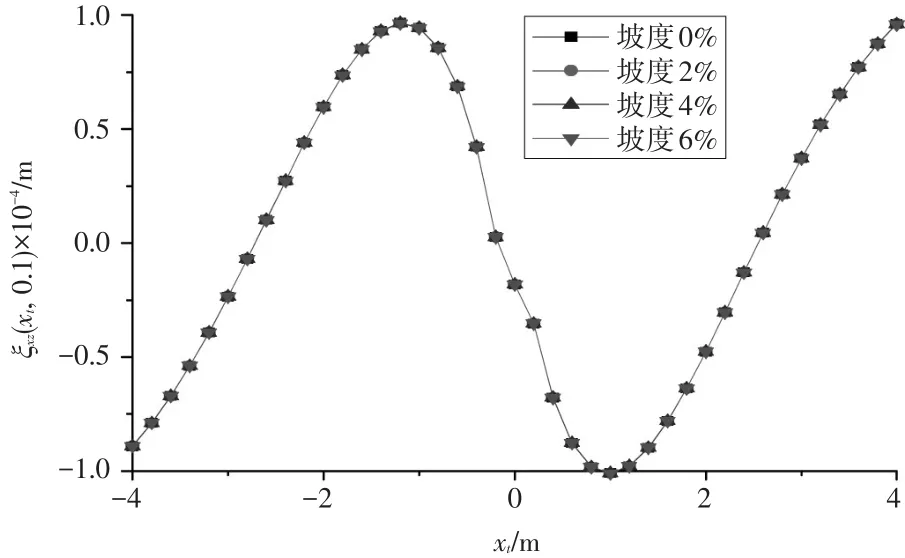
图13　不同坡度下水平位移沿着水平方向的变化规律

从图10可以看出，在xt为-1~1m处正应力出现剧烈变化，在较远处变化相对较平缓，并且在xt=0处正应力达到最大值，且其峰值为正值（面层受拉），即拉应力区集中出现在面层荷载作用中心处。整体来看，正应力沿水平方向先减小后增大，路面在不同的坡度条件下，当纵坡坡度由0增大到6%时，正应力几乎没有发生变化，最大正应力产生的位置也没有变化。这就说明，当车辆在不同坡度的路面行驶时，纵坡对面层正应力的影响响应程度是不显著的。

从图11可以看出，当荷载移动距离xt为1～4m时，剪应力迅速减小，最后等于0；当荷载移动距离xt=1m时，剪应力急剧变化；当荷载移动距离xt= 0时，剪应力接近于0；在荷载边缘（xt=±0.1m）处，面层中的剪应力达到最大值，方向相反。整体来看，剪应力沿路面水平方向变化规律相反，同时路面在不同的坡度条件下（纵坡坡度由0增大到6%），水平应力几乎没有发生变化，最大水平应力产生的位置也没有变化。

从图12可以看出，当荷载移动距离xt为0～4m时，孔隙水压力沿着水平方向先减小后增大；当荷载移动距离在xt为-1～1m时，孔隙水压力急剧变化，在面层底部，孔隙水压力接近于0，最大孔隙水压力出现在荷载作用中心处（xt=0）。整体来看，路面在不同的坡度条件下（纵坡坡度由0增大到6%），孔隙水压力几乎没有发生变化，最大孔隙水压力产生的位置也没有变化，这就说明，当荷载在不同坡度的道路上行驶时，路面内孔隙水压力沿着路面水平方向的响应程度微乎其微。

从图13可以看出，当荷载移动距离xt为1～4m时，水平位移随着水平方向长度增大而增大；当荷载移动距离xt为0～1m时，水平位移随着水平方向长度的增大而减小。当荷载移动距离xt=0时，水平位移为0。当荷载移动至离开观察面后，这种变化趋势相反。由此可知，在荷载移动过程中，面层水平位移沿着水平长度的变化幅度是不相同的，越接近观察面，这种变化幅度就越大。整体来看，不同纵坡坡度所对应的水平位移几乎相同，所以说，纵坡坡度对面层的水平位移的影响响应比较微弱。

3　结论

（1）车辆荷载对正应力、孔隙水压力、剪应力和位移的影响

沿着面层深度方向，面层竖向应力、孔隙水压力、剪应力和竖向位移都随着车辆荷载的增大而增大；沿着面层水平方向，水平应力、孔隙水压力、剪应力和水平位移也是随着车辆荷载的增大而增大。这就说明，超载对正应力、剪应力、位移和孔隙水压力的影响是非常显著的。

（2）荷载移动速度对正应力、孔隙水压力、剪应力和位移的影响

沿着面层深度方向，荷载移动速度对竖向应力几乎不产生影响，对孔隙水压力、剪应力和位移产生显著影响，荷载移动速度越大，面层孔隙水压力就越大，面层竖向位移就越小，面层顶面和底面产生的剪应力也就越小；沿着面层水平方向，荷载移动速度对剪应力和水平位移的影响不明显，对正应力和孔隙水压力的影响显著，面层水平应力和孔隙水压力随着荷载移动速度的增大而增大。

（3）纵坡坡度对正应力、孔隙水压力、剪应力和位移的影响

通过数值计算可知，正应力、孔隙水压力、剪应力和位移几乎不受纵坡坡度的影响。

[1]Dawson A.Water in Road Structure[M].Berlin:Springer, 2008.

[2]傅搏峰，周志刚，陈晓鸿.沥青路面水损害疲劳破坏过程的数值模拟分析[J].郑州大学学报：工学版，2006，27（1）：51-58.

[3]欧金秋.沥青路面水损坏的动水压力驱动机理研究[D].济南：山东大学，2012.

[4]董泽蛟，谭忆秋，曹丽萍，等.水-荷载耦合作用下沥青路面孔隙水压力研究[J].哈尔滨工业大学学报，2007，39（10）：1614-1617.

[5]罗苏平，但汉成.移动交通荷载下饱和沥青路面的水力耦合分析[J].华南理工大学学报，2012，40（2）：105-107.

[6]但汉成，李亮，杨小礼.基于渗流理论的沥青路面渗入率计算与分析[J].中南大学学报：自然科学版，2010，41（2）：742-748.

[7]Verruijt A.An Introduction to Soil Dynamics[M].Berlin: Springer,2010．

[8]Theodorakopoulos D D.Dynamic Analysis of a Poroelastic Half-Plane Soil Medium under Moving Loads[J].Soil Dy⁃namics and Earthquake Engineering,2003,23(7):521-533.

[9]Siddharthan R,Zafir Z,Norris G M.Moving Load Response of Layered Soil.Ⅰ:Formulation[J].Journal of Engineering Mechanics-Asce,1993,119(10):2052-2071.

[10]Siddharthan R,Zafir Z,Norris G M.Moving Load Response of Layered Soil.Ⅱ:Verification and Application[J].Journal of EngineeringMechanics-Asce,1993,119(10):2072-2089.

[11]薛强，盛谦.沥青路面破坏的多场耦合效应及控制技术[M].北京：科学出版社，2009.

[12]Jin B.Dynamics Response of a Poroelastic Half Space Gener⁃ated by High Speed Load[J].Chinese Quarterly of Mechan⁃ics,2004,25(2):168-174.

Coupled Hydro-MechanicalAnalysis of SaturatedAsphalt
Pavement at Longitudinal Long Slope under Moving Traffic Loads

WANG Hai-feng1,DAN Han-cheng2,TENG Xu-qiu3
(1.Ningxia Highway Construction Administration,Yinchuan 750000,China; 2.School of Civil Engineering,Central South University,Changsha 410075,China; 3.Lanzhou Jiaotong University,Lanzhou 730070,China)

In order to reveal the mechanism of water-induced damage to longitudinal slope saturated as⁃phalt pavement,based on the Biot Consolidation Theory and characteristics of the longitudinal slope in rainy regions,the hydro-mechanical coupled mode and hydro-mechanical coupled governing equations with two-dimensional three-layer system of"Surface-Base-Subgrade"of saturated asphalt pavement be⁃ing subject to moving traffic loads were established.With the boundary condition that the bottom of the surface could completely drain,the influence of vehicle load,driving speed and longitudinal slope on dis⁃tribution of normal stress,pore-water pressure,shear stress,surface course displacement and other phys⁃ical quantities were analyzed comprehensively and systematically,offering the theoretical foundation and reference to the design of longitudinal slope asphalt pavement structure.The results show that the vehi⁃cle load and moving traffic loads speed have significant influence on the normal stress,pore water pres⁃sure,shear stress and surface displacement,and the longitudinal slope has almost no impact on the nor⁃mal stress and pore water pressure,shear stress and surface displacement.

longitudinal long slope;saturated asphalt pavement;moving traffic load;hydro-mechan⁃ical coupling;pavement structure design

U416.01

A

2095-9931（2015）02-0081-09

10.16503/j.cnki.2095-9931.2015.02.015

2015-01-20

王海峰（1986—），男，硕士，助理工程师，主要研究方向为路基路面工程。E-mail：465654568@qq.com。