电力系统暂态稳定性闭环控制(六)
——控制地点的选择
张保会,王怀远,杨松浩
(西安交通大学 电气工程学院,陕西 西安 710049)
0 引言
在电力系统遭受大扰动后,需要对系统施加一定的控制措施[1-9]才能使得系统恢复稳定,当确定控制量之后,控制地点的选择关系到控制的有效性和经济性。文献[4]论述了切机地点要选择在超前失稳机群中,避免切被动失稳机组的阻止失稳的控制效果,本文将探讨如何根据实测信息选择有效的切机地点。
切机地点的选择是在超前失稳机群中进行,而超前失稳机群中往往有很多发电机组,不同的发电机组控制效果各有差异,因此有必要研究如何根据发电机的实时信息,避免具有控制负效应[10-12]的机组,选择有效的切机地点。
目前切机地点的实时选择主要是根据经验的方式得到[13-14],或根据超前失稳机群中各发电机组的暂态动能排序进行切机,或根据其功角大小排序进行切机,或优先选择距离故障位置电气距离较近的机组,然而这些切机地点的选择方法,随着故障类型和运行方式的不同,得到的切机效果也是时好时坏。
本文根据发电机的实时响应信息,依据发电机的有符号动能和功角的组合进行排序,得到初始有效切机地点集合;再通过计算等值机械功率切机前后的变化,剔除超前失稳机群中的被动失稳机组,得到最终的切机地点实时选择方法。在IEEE 39节点系统和三华联网系统的仿真中,通过对比3种不同切机地点的实时选择方法,验证了本文提出的切机地点选择方法的有效性。
1 切机地点的选择排序
目前在仿真计算控制措施时,常采用优先切除暂态动能最大[8-9]、功角摆开最大或距离故障点电气距离最近的机组。以上切机选择原则经本文仿真,其效果在多种失稳场景下,不能保证阻止失稳效果最好。分析其阻止失稳效果不是最好的原因,有以下几个方面。
a.优先切除暂态动能最大的机组:按照能量函数的方法分析系统的暂态稳定性,暂态不稳定是由于故障形成的系统暂态能量无法完全被系统所吸收,系统在控制不稳定平衡点处的动能不能被完全转化为势能,具有多余动能而失稳。如果能够减少系统的多余动能,使之在控制不稳定平衡点前完全转化为势能,则系统可以稳定。依据以上观点,在计算控制措施时,优先切除暂态动能最大的机组。然而,暂态动能最大的机组不一定距离控制不稳定平衡点最近,切除它们的同时其他机组可能已经越过不稳定平衡点,无法阻止不稳定了[15]。
b.优先切除功角摆开最大的机组:功角最容易摆开的机组往往是惯性较小的机组,也有可能它已经开始减速了,或对于等值系统角度持续摆大的贡献较小,切除它对于阻止失稳作用不明显。
c.优先切除距离故障点较近的机组:距离故障点较近的机组有可能是滞后群A中的机组,可能是被动失稳机组,也可能是惯性较小的机组等。
总结以上方法的优点和不足,本文提出的切机优先原则为:机组动能大、距离控制不稳定平衡点较近且在加速中的机组。对于超前失稳的情况,切除机组的动能越大,系统需要吸收的暂态能量越小,越能体现控制效果;发电机相对超前群局部惯性中心的功角为正值且较大时,表示该发电机有可能会率先达到不稳定平衡点而发生失稳;如果该发电机的角速度也为正值,表示该发电机还要以更快的速度到达、越过控制不稳定平衡点。
归纳以上分析,提出一个指标Wc(i),综合考虑发电机的暂态动能和功角的影响:
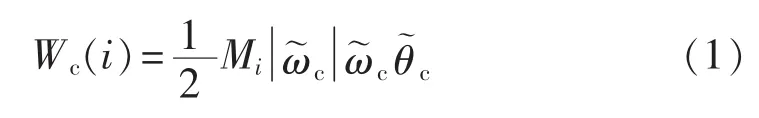
Wc(i)的计算考虑了发电机组临界机群局部惯性中心坐标下角速度的正负,可以避免一些相对减速的机组。 选择 Wc(i)大于零的发电机组,并按照 Wc(i)大小排序,超前失稳机群中发电机组初始的切机顺序集合记为:

其中,S为临界机群机组。
2 剔除被动失稳机群
多机电力系统的失稳是由超前失稳机群的暂态能量主导的,而超前失稳机群还可分为主动失稳机群和被动失稳机群[7]。主动失稳机群是由受扰程度比较严重从而直接导致系统失稳的发电机组成,而被动失稳机群是指受主动失稳机群的作用力影响而被动失稳的机群。为了快速有效地阻止系统失稳,切机控制地点应避免被动失稳机群中的发电机,切机措施切除了发电机的部分机械功率PM和机组的转动惯量,因此执行切机操作时,不仅仅需要考虑各机组的功角、角速度等信息,还需要考虑切除的转动惯量对超前机群加速功率的影响。由于切机措施不仅仅切除了机组的机械输入功率,同时也影响了系统的惯性时间常数,受惯性时间常数的影响,当超前失稳机群中的某台发电机被切除后,等值系统的等值机械输入功率P′M有时反而会增大,使系统的稳定性恶化,这样的机组就是被动失稳机组。因此,在候选切机地点中应剔除切机后系统等值机械功率反而增大的被动失稳机组。
回顾文献[2]中多机系统等值为单机无穷大系统的等值式:
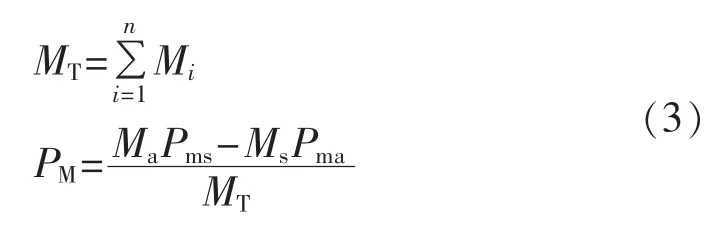
其中,Ms和Ma分别为超前机群S和落后机群A的等值惯量;Pms和Pma分别为S和A群的等值机械输入功率;n为全系统机组总台数;MT为所有机组的转动惯量之和。
当发电机被切除时,该发电机的机械功率和转动惯量在等值系统中作用均为零。因此为寻找被动失稳机组,可以通过假设逐次切除超前机群S中的每台发电机,来观察其对等值系统机械输入功率P′M的影响。假定第i台发电机被切除,则等值机械功率P′M变为:
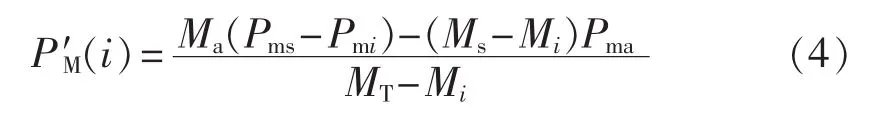
其中,Pmi为第i台发电机的机械输入功率。以上实测参数都是已知的。
如果 P′M(i)>PM,则第 i台发电机就是被动失稳机组,应该从候选切机S群中剔除这台发电机。
因此在初始切机顺序集合 Ω(i)中,由 P′M(i)<PM的机组形成主动失稳机群,被切机组在以下集合中选取,记为:
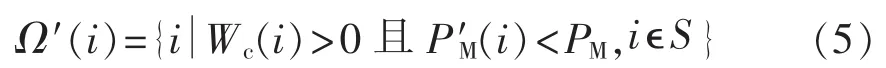
将 Ω′(i)中的所有发电机按照 Wc(i)从大到小的顺序进行排序便可得到最终切机地点排序表。当切机控制量ΔPm确定后,可取总容量大于ΔPm且最接近于ΔPm的切机地点排序表中的前几台发电机作为最终的切机控制策略。
3 仿真
3.1 剔除被动失稳机组
以IEEE 39节点系统为例进行仿真,系统接线图如图1所示。
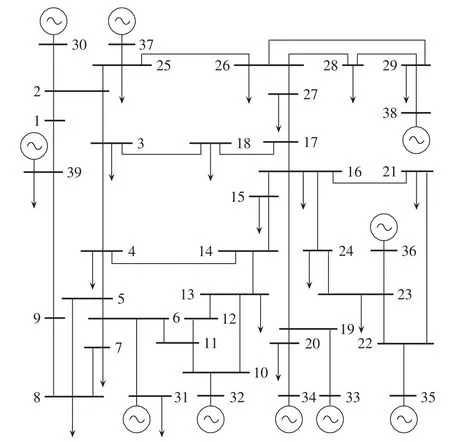
图1 IEEE 39节点系统接线图Fig.1 Wiring diagram of IEEE 39-bus system
故障设置为母线13和母线14之间线路0 s发生三相短路故障,0.2 s断开线路切除故障。系统的功角摇摆曲线图如图2所示,超前失稳机群为发电机G31和G32。
由文献[2]的方法分群,得到超前机组中有2台发电机 G31和 G32,在 0.4 s 判出系统不稳定[1-3],假设0.45 s时完成切机,由文献[5]的方法算得切机量550 MW,因此需要剔除控制负效应的发电机,将2台发电机信息代入式(4)中得到表1(表中数据为标幺值)。
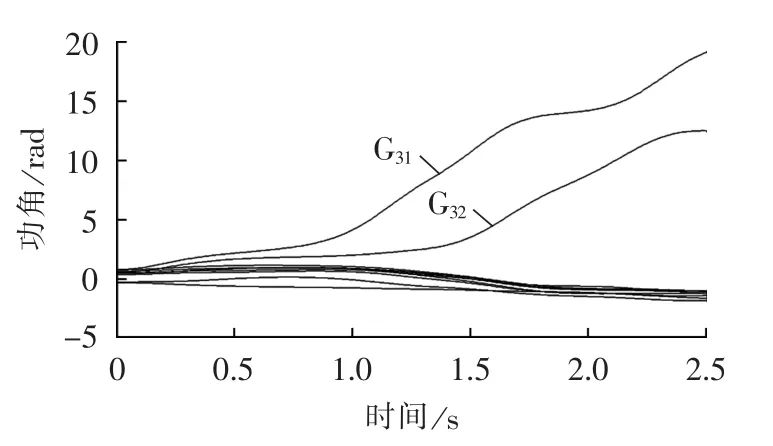
图2 线路13-14发生故障后的功角失稳图Fig.2 Power angle curves when line 13-14 has fault

表1 切机后系统等值机械功率Table 1 Equivalent mechanical power after generator-shedding
最后的切机措施为切除发电机G31550 MW(即60%)有功出力,摇摆曲线如图3所示,切机量合适,系统保持稳定。
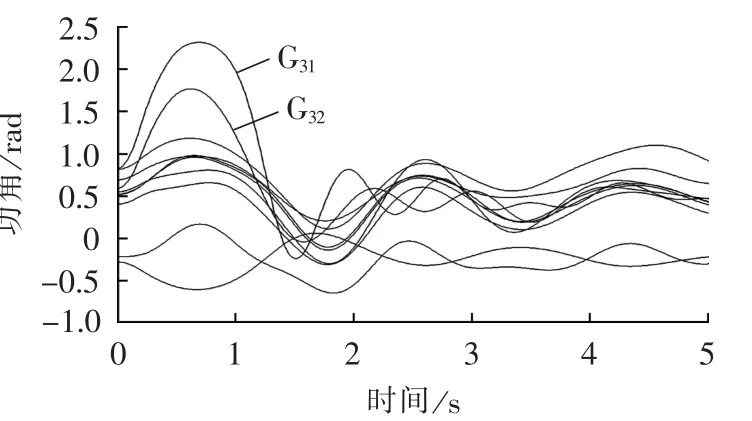
图3 切除发电机G31550 MW的功角稳定图Fig.3 Power angle curves,with 550 MW of G31shed
如果不剔除被动失稳机组G32,在0.45 s时切除发电机G31550 MW和发电机G32200 MW的有功出力,功角曲线如图4所示,系统仍然失稳。比较图3与图4的切机方案,尽管图4方案多切除了G32的发电量200 MW,反而将系统控制得不稳定了。可以看出,G31是有效的控制机组,而G32是具有控制负效应的机组,通过式(4)可以准确剔除该被动失稳机组。
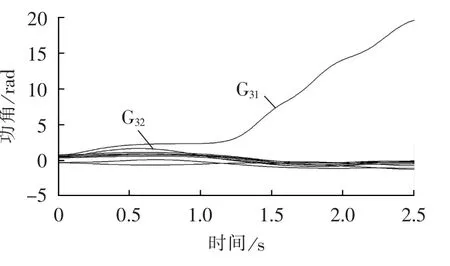
图4 切除G31550 MW和G32200 MW的功角失稳图Fig.4 Power angle curves,with 550 MW of G31 shed and 200 MW of G32shed
3.2 考察切机地点选择的正确性
考察切机选择原则为:方案1按照动能大小排序切除,方案2按照功角大小排序切除,方案3按照本文排序原则切除。比较切除相同容量而被切机组不同,阻尼系统失稳的效果不同。
3.2.1 IEEE 39节点系统
双重故障设置为母线15和母线16之间线路0 s发生三相短路故障,0.35 s断开线路切除故障,同时母线21和母线22之间线路0 s发生三相短路故障,0.2 s断开线路切除故障,系统的功角摇摆曲线图如图5所示。由文献[2]的方法分群,得到超前机群包含G31—G38这8台机组,并在0.38 s判别出系统将要失稳,若控制措施在0.43 s完成,用文献[5]的方法求得的切机控制量为1400 MW。
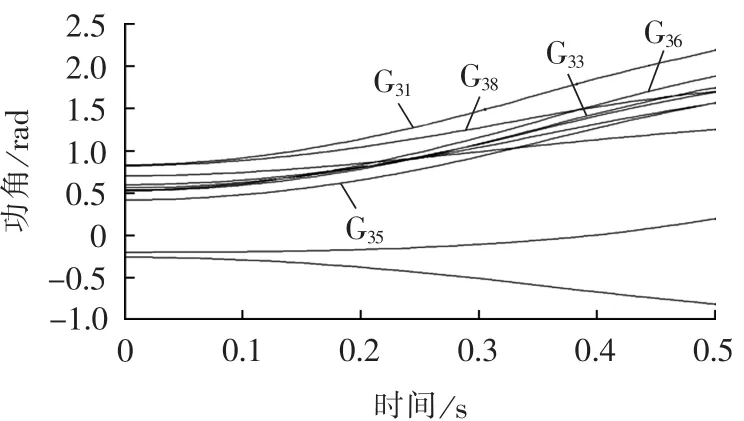
图5 线路15-16、21-22间双重故障后的功角失稳图Fig.5 Power angle curves when line 15-16 and line 21-22 both have fault
列出3种不同的切机地点选择方法,其切机地点与切机容量如表2所示,表中括号中的百分数表示切除容量占装机容量比例,切机控制后的系统功角曲线图如图6—8所示,可以明显看出,方案1、2的切机容量大于1400 MW时仍不能阻止系统失稳,而按照本文的切机选择原则,当切除1331 MW时已经阻止了系统失稳,切机控制的效果最好,切除的容量也最小。
3.2.2 三华联网系统
在三华联网系统对所得的控制地点选择方法进行仿真,故障设置为洪沟—板桥发生短路接地故障0.1 s跳开双回线。由文献[2]的分群及不稳定判别方法,在0.94 s时得到系统将要失去稳定的切机启动信号,切机控制在0.3 s之后,即1.24 s时完成。
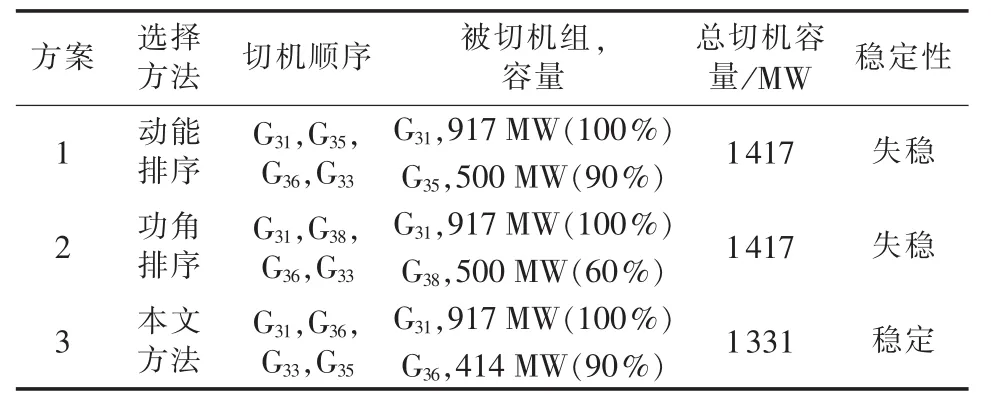
表2 IEEE 39节点系统切机方案及效果对比表Table 2 Comparison of generator-shedding scheme and effect for IEEE 39-bus system
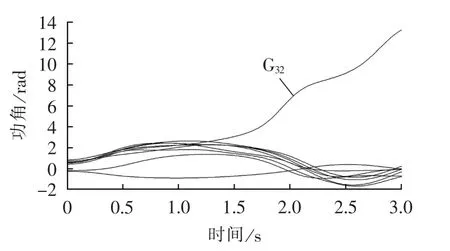
图6 方案1切除发电机G31和G35的功角失稳图Fig.6 Power angle curves of scheme 1,with G31and G35shed
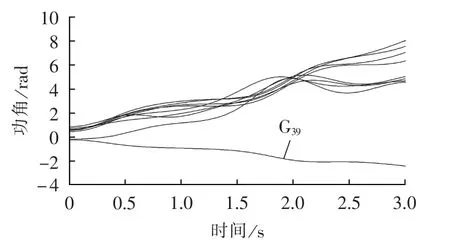
图7 方案2切除发电机G31和G38的功角失稳图Fig.7 Power angle curves of scheme 2,with G31and G38shed

图8 本文方案切除发电机G31和G36的功角稳定图Fig.8 Power angle curves of proposed scheme,with G31and G36shed
对比3种不同的控制地点选择方法:方案1是按照机组暂态动能的排序,共切除4415 MW机械功率;方案2是根据相对于惯性中心的功角进行排序,切除了4 412 MW机械功率;方案3是按照本文提出的方法,按照机组的有符号动能和功角的乘积进行排序,并剔除具有控制负效应的机组,共切除4568 MW机械功率。控制后的系统功角曲线图如图9—11所示,控制效果的对比如表3所示。
由表3可以看出,方案1和方案3可以使得系统恢复稳定,且方案3的控制效果要优于方案1,而方案2按照功角的排序进行选择无法使得系统恢复稳定。方案3综合考虑了发电机组的暂态动能和功角,所需要的参数也都可以通过广域测量系统得到,运算速度快,控制效果相对较好,可以适用于在线实时控制中。
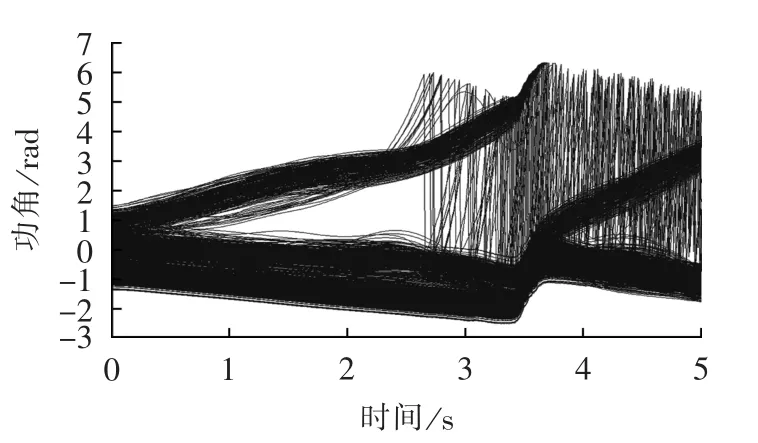
图9 方案1的控制效果Fig.9 Control effect of scheme 1
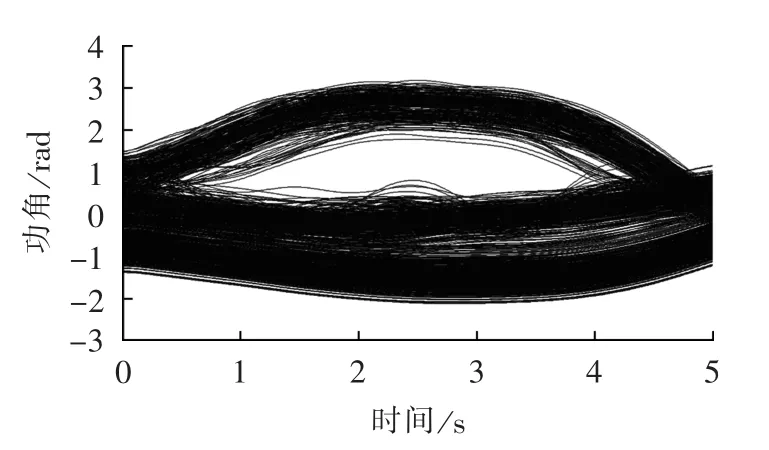
图10 方案2的控制效果Fig.10 Control effect of scheme 2
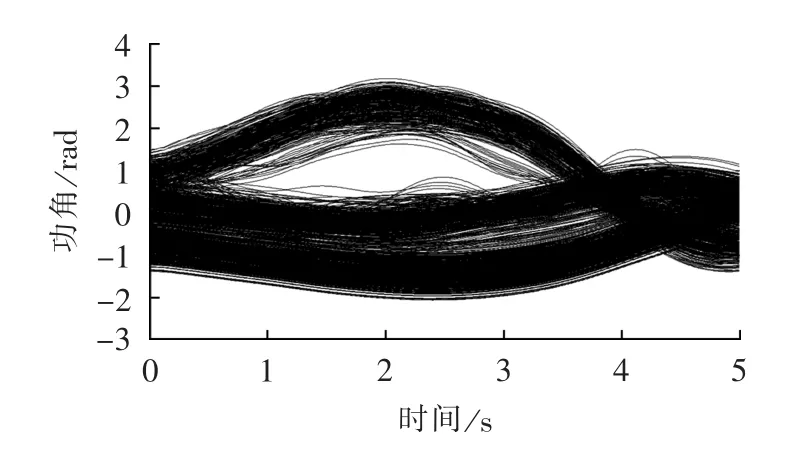
图11 方案3的控制效果Fig.11 Control effect of scheme 3
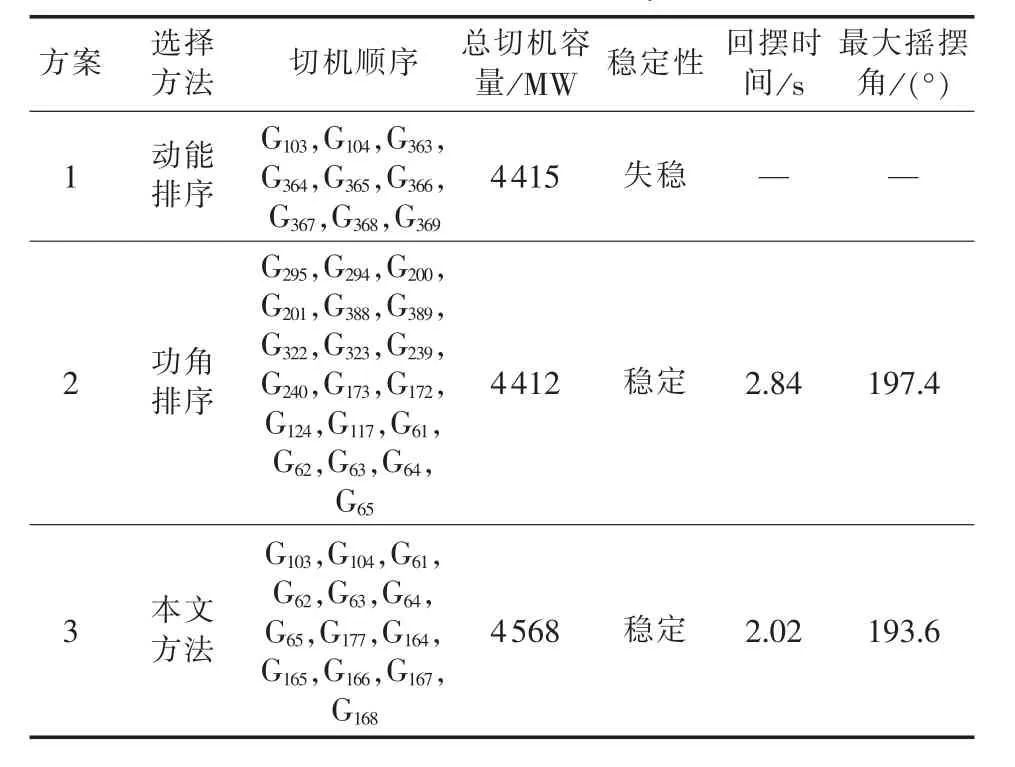
表3 三华系统切机方案及效果对比表Table 3 Comparison of generator-shedding scheme and effect for Sanhua System
4 结论
暂态稳定性闭环控制的效果与控制量的作用位置紧密相关,本文根据发电机组有符号动能与功角的乘积的大小对被切机组进行排序,并通过切机后等值机械功率变大剔除具有控制负效应的机组,在以上切机序列中选出满足文献[5]计算所得的切机量进行切机控制。在IEEE 39节点系统和三华联网系统的仿真,验证了本文提出的控制地点选择方法的有效性。

