混合蛙跳在网络编码协作系统资源分配的应用

刘紫燕，唐思腾，冯 丽，毛 攀，张达敏

(1.贵州大学 大数据与信息工程学院，贵州 贵阳550025;2.国网重庆市电力公司，重庆400014)

协作通信系统通过节点协作传输信号来获得空间分集增益，能有效提高系统的传输速率和吞吐量［1］。由于协作中继系统采用半双工工作方式，物理层网络编码(PNC)被应用到双向中继协作系统提高频谱效率，相比传统的双向中继协作系统，采用PNC 协议的系统一次传输仅需要两个时隙就能完成点对点通信。在节点的转发方式上，放大转发AF(Amplify and Forward)只需将源节点的信息直接做放大处理，简单易实现，更容易在实际系统中实现。此外，由于OFDM 技术能克服多径衰落，所以基于PNC－AF 的OFDM 协作系统有很大的研究意义。

资源分配能有效提高OFDM 双向中继协作系统的性能［2－4］。文献［5］研究了QoS 约束下OFDM 双向中继协作系统的资源分配，然而没有考虑AF 中继协作方式，文献［5］研究了QoS 约束下OFDM 双向AF 中继协作系统的资源分配问题。混合蛙跳算法［6－7］将局部搜索和重新混合过程相间进行，有效地将全局信息交互和局部进化搜索相结合，具有高效的计算性能和优良的全局搜索能力。已有的OFDM 双向AF 中继系统资源分配文献中，还没有考虑混合蛙跳算法对资源分配的优化。本文考虑文献［6］中基于能效的资源分配模型，利用混合蛙跳算法优化系统资源。

本文将混合蛙跳算法引入到网络编码协作的多中继通信系统中，在考虑系统能量效率的情况下，以最小化系统传输功率为目标，利用混合蛙跳算法搜索的优势，实现节点的资源分配，降低了系统的传输功率，使系统性能得到优化。该资源分配算法不受优化目标函数特性的影响，能实现快速优化，算法简单，收敛速度快。

1 系统模型及问题论述

1.1 系统模型

考虑基于网络编码的双向多中继协作OFDM 系统。如图1 所示，一个源节点S 通过K 个中继节点Rk(k=1，2，…，K)与目的节点D 进行通信。每个中继节点R 采用PNC－AF转发协议和半双工工作方式进行转发信息。每个信道被划分为N 个相互正交的子信道，为了方便，假设每个信道的信道状态信息都已知，且每个子信道经历独立的平坦衰落。S 和D 交换一次信息只需要两个时隙，第一个时隙:R 通过子载波i(i=1，2，…，N)同时接收S 和D 发送的信息，第二个时隙，R将接收的信息进行XOR 操作后，通过子载波j(j=1，2，…，N)同时转发给S 和D，子载波i 可能不等于子载波j，形成子载波对(i，j)。为了避免干扰，每个子载波对分配给一个中继，记第k 个中继上的子载波对为(i，j，k)。和分别为S 和D通过子载波i 到中继Rk的信道因子，同时和分别为Rk通过子载波j 到中继S 和D 的信道因子。

图1 系统模型

第i 个子载波在中继k 上的放大因子［5］为

因此，通过第k 个中继转发，在子载波对(i，j)上的S 到D以及D 到S 的信息速率分别为

1.2 问题论述

记ρi，j∈(0，1)为子载波对分配因子，若第一跳第i 个子载波成功配对第二跳第j 个子载波，则ρi，j=1;相反，则ρi，j=0。记rs，i，j和rd，i，j为S 到D 以及D 到S 链路所要求的信息速率。在子载波配对过程中，每个子载波只能唯一配对另一个子载波，因此变量ρi，j必须满足如下约束条件:

子载波约束条件为

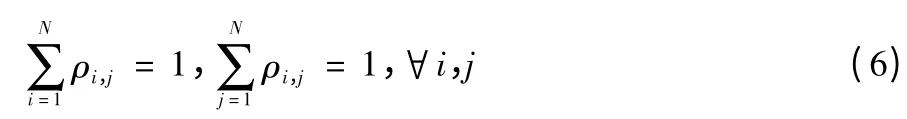
双向多中继OFDM 系统的总功率为

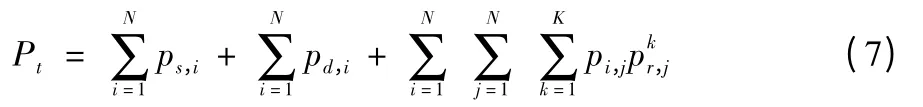
最优化问题

为了满足用户QoS，由约束条件可知

在满足用户QoS 下，由式(9)、(10)可知，最小节点功率为

由式(1)、(4)、(5)、(11)、(12)可得出最优âki的表达式为

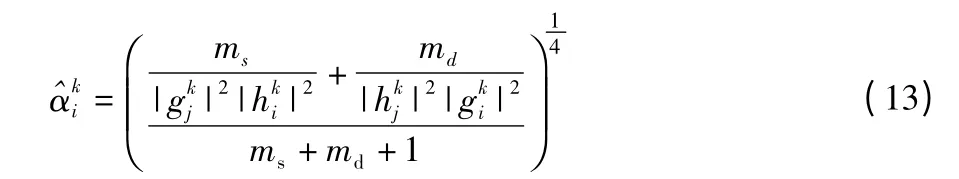
式中:ms=－1，md=－1。从式(1)、(11)、(12)、(13)可以得出

由式(11)、(12)、(14)重写式(8)的最优化问题为

2 基于混合蛙跳的资源分配算法

2.1 交换子和交换序［7］

1)交换子

假设n 个节点的资源分配解序列为sNode=(sNodei)，i=1，2，…，n。定义交换子swap(i1，i2)为解序列sNode 中的点sNode1和sNode2，则为解sNode 经过算子swap(i1，i2)操作后的新解。

例如有4 个子载波，记sNode=(1，2，3，4)为某条链路的待分配子载波，若交换子为swap(2，3)，则经过这个交换子运算后，得到的新解为

这里为符号“+”赋予了新的含义:经过算子swap(i1，i2)操作后，sNode 中的i1和i2进行交换，符号“+”记为交换操作。

2)交换序

不同的解序列相互作用，形成一个或多个交换子所构成的有序序列即为交换序，记为SwapQ，即

式中:swapi(i=1，2，…，n)为其中一个交换子。交换子之间的先后顺序是有意义的，不同顺序的交换子作用于同一个解会得到不同的解序列。交换序作用于某个解序列，意味着交换序中的交换子依次作用于这个解序列，记为

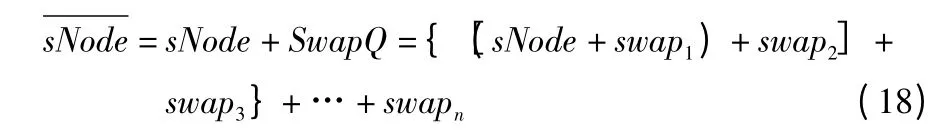
3)交换序的构造

若两个交换序SwapQ1和SwapQ2作用于同一个解sNode得到的新解相同，则记为等价交换序列集，在等价交换序列中，最少交换子的交换序称为基本交换序。所以构造交换序只需构造基本交换序即可，假设两个解序列sNodeA 和sNodeB，其基本交换序为swap，满足sNodeA=sNodeB+swap。sNodeA=(1 2 3 4);sNodeB=(4 3 1 2)。

基本交换序流程如图2 所示，构造交换序举例如下:

1)sNodeA(1)=1，查看sNodeB 中各值可以看出，sNodeB中的第3 个位置需要和第1 个位置交换才能使sNodeA(1)=sNodeB(1)，所以第1 个交换子为swap1(1，3)，得到sNodeB1=sNodeB+swap1(1，3)=(1 3 4 2);

2)sNodeA(2)=2，查看sNodeB 中各值可以看出，sNodeB1中的第2 个位置需要和第4 个位置交换才能使sNodeA(2)=sNodeB1(2)，所以第2 个交换子为swap2(2，4)，sNodeB2=sNodeB1+swap2(2，4)=(1 2 4 3);

3)sNodeA(3)=3，查看sNodeB 中各值可以看出，sNodeB2中的第3 个位置需要和第4 个位置交换才能使sNodeA(3)=sNodeB2(3)，所以第3 个交换子为swap3(3，4)，sNodeB3=sNodeB2+swap3(3，4)=(1 2 3 4);

4)sNodeA(4)= sNode23(4)，即sNode=sNode3，经过以上步骤，基本交换序为

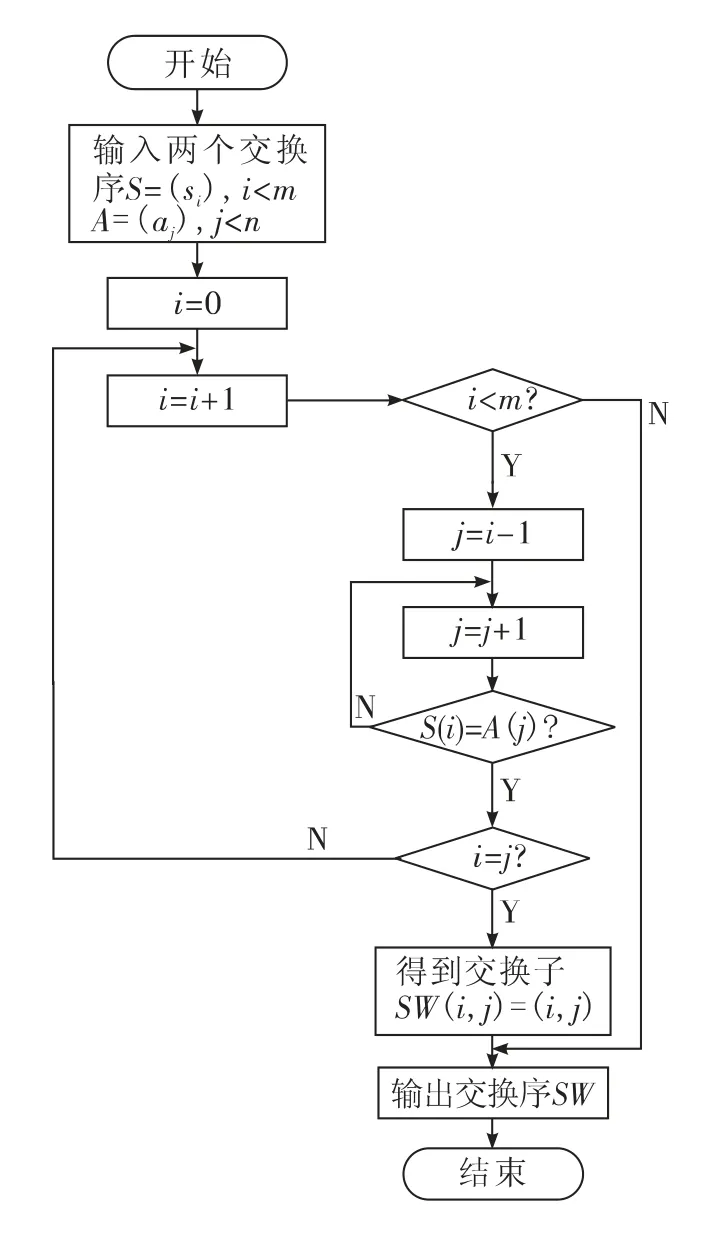
图2 基本交换序构造流程

这里为符号“－”也赋予了新的含义，即sNodeA 和sNodeB进行操作后，得到一个交换序，符号“－”记为交换操作。

2.2 基于交换序的混合蛙跳算法

基本的SFLA［8－9］速度公式和位置更新公式不能满足资源分配问题，将交换子和交换序的概念引入到SFLA 中，重新定义速度公式和位置更新公式如下:

速度公式为

式中:rand 是在［0，1］之间的随机数;Pib(t－1)是前一时刻种群最好位置的青蛙;Piw(t－1)是前一时刻种群最坏位置的青蛙。式(20)表示操作后得到的青蛙的移动速度以概率rand被保留下来，V(t)是当前时刻青蛙的移动速度。这里符号“－”为交换操作，例如:Pib(t－1)=(1 2 3 4);Piw(t－1)=(4 3 1 2)，则V(t)=Pib(t－1)－Piw(t－1)={1 3 2 4 3 4}。

位置更新公式(最坏青蛙进化后)为

式中:Piw(t)表示经过交换序V(t)操作后得到的新解序列;Vmax表示青蛙的最大移动速度。这里符号“+”为交换操作，若Piw(t－1)=(4 3 1 2)，V(t)=Pib(t－1)－Piw(t－1)={1 3 2 4 3 4}，则Piw(t)=Piw(t－1)+(1，3)+(2，4)+(3，4)={1 2，3，4}。

2.3 基于混合蛙跳算法的功率分配流程

步骤如下:

1)初始化。选择模因组数目m_Memeplex;每个模因组中的青蛙数目m_frog，整个蛙群大小满足F=m_Memeplex×m_frog;种群迭代次数MAXGEN 和模因组内迭代次数Ne。

2)构造模因组。生成F 个青蛙U(1)，U(2)，…，U(F)。每一个青蛙表示解空间的一个候选解，计算每一个青蛙U(ib)的适配值fitness，即总传输功率。

3)整个蛙群排序。按2)中计算的适配值对整个蛙群的青蛙进行升序排列，因此，U(1)就代表了整个种群中最好的青蛙。

4)构建模因组Y。对青蛙进行分组，分组方式为

5)模因组进化，即对每个模因组内的最差的青蛙进行局部搜索。

模因组进化(局部搜索)流程如下:

(1)设置im=0 表示种群计数，最大值为模因组数目m，满足0≤im≤m。设置iN=0 为种群进化次数，最大值为每个模因组青蛙的数目N，满足0≤iN≤N。

(2)im=im+1。

(3)iN=0。

(4)iN=iN+1。

(5)改善最坏青蛙位置:模因组内青蛙根据式(20)和(21)来更新自己的移动距离和位置。如果新青蛙的适配值较原来的适配值好，则用新产生的青蛙Pib(t)代替原来的青蛙并跳转到步骤(4)，否则，用U(1)代替Pib(t－1)重新计算青蛙的位置和适配值，如果还没有改善，则随机产生一个新的青蛙r 取代原来的青蛙。计算fitness=f(r)。

(6)更新模因组。将模因组按降序排列。

(7)如果iN ＜N，跳转到(4)。

(8)如果im ＜m，跳转到(2)，否则，返回到全局搜索。

6)整个蛙群进化:将青蛙混合，即青蛙在模因组之间跳跃。当每个模因组内完成进化之后，将各个子群Y1，Y2，…，Ym重新混合成X，即X={Yk|k=1，2，…，m_frog}。将X 按升序排列，更新种群中最好的青蛙Px。

7)迭代终止条件。如果满足迭代条件，则输出结果，否则转到步骤3)。一般而言，当迭代到一定次数后，代表最好解的青蛙位置就不会再改变，跳出循环。也可以设置迭代次数来作为循环终止条件。

3 仿真结果与分析

为了验证本文算法的性能，本文仿真对比了其他两种资源分配方案:基于第一跳最优子载波(Optimal Subcarrier for First Hop)资源分配方案、固定子载波对(Fixed Subcarrier Pairing)分配方案。

假设在静态瑞利信道无线环境下对资源分配方案进行仿真，源节点与目的节点的距离为3 km，随机分配5 个中继，具体位置如表1 所示。子载波数N=16，路径损耗因子为3，混合蛙跳的参数设置如表2 所示。

表1 中继位置

表2 混合蛙跳参数设置

图3 比较了第一跳和第二跳的信息速率相等时，基于混合蛙跳(SLFA)的资源分配方案、基于第一跳最优子载波(Optimal Subcarrier for First Hop)资源分配方案、FSP(Fixed Subcarrier Pairing)分配算法下的总传输功率。从图中可以看出，当第一跳和第二跳的总信息速率相等时，即R1=R2，3 种资源分配方案下系统所的传输功率随链路的速率增大而增加。在相同的信息速率下，基于SLFA 的资源分配方案比其他两种资源分配方案所需的传输功率少。

图3 相同速率下3 种资源分配方案的传输功率比较

图4 比较了第一跳和第二跳的信息速率不相等时基于混合蛙跳的资源分配方案、基于第一跳最优子载波资源分配方案、FSP 分配算法下的总传输功率。总信息速率不变，即，第一跳的信息速率R1占总传输功率比例分别设置为［0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9］，可以明显看出，当R1=R2时，3 种资源分配方案下系统所需的传输功率最少;此外，本文提出的基于混合蛙跳(SLFA)的资源分配方案优于基于其他两种资源的分配方案。

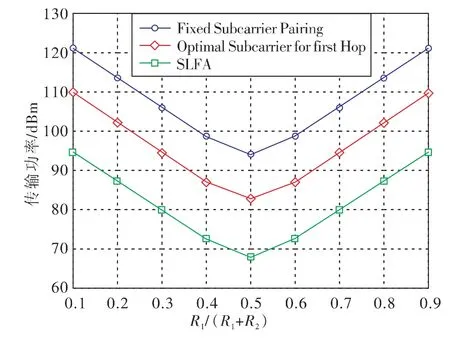
图4 不同速率下3 种资源分配方案的传输功率比较

图5 比较了在不同中继协作个数下基于混合蛙跳(SLFA)资源分配方案的总传输功率。从图中可以看出，设置中继个数为{2，4，6，8}，在相同的环境下，参与协作的中继个数越少，传输功率越小;当协作中继数目为2 时，此时系统消耗的功率最少。

图5 不同中继协作下基于SFLA 资源分配方案的传输功率比较

4 结论

本文针对双向OFDM 多中继协作通信系统，以最小化传输功率为目标提出了基于混合蛙跳算法的资源分配策略，利用混合蛙跳算法求解出每一跳链路的最优子载波对和最小功率。当第一跳和第二跳速率相同时并且采用较少的中继数，基于混合蛙跳算法的资源分配方案所需的功率最小;与基于第一跳最优子载波资源分配方案、固定子载波对分配方案相比，本文提出的基于混合蛙跳算法的资源分配方案更节省能量，该算法为多中继协作通信系统的资源分配提供了一种优化解决方案。

［1］KRISHNA R，CUMANAN K，XIONG Z L，et al. A novel cooperative relaying strategy for wireless networks with signal quantization［J］.IEEE Trans.Vehicular Technology，2010，59(1):485－489.

［2］ZHAO Hanhua，ILOW J. Adaptive resource allocation in OFDMA relay networks with network coding［C］//Proc. IEEE International Conference on Communications.［S.l.］:IEEE Press，2011:1－5.

［3］XIONG Ke，FAN Pingyi，LETAIEF B，et al. Resource allocation for minimal downlink delay in two－way OFDM relaying with network coding［C］//Proc. IEEE International Conference on Communications.［S.l.］:IEEE Press，2012:5343－5347.

［4］刘紫燕，唐思腾，冯亮，等.多中继协作系统量子遗传算法的功率分配仿真［J］.电子技术应用，2014，40(11):113－115.

［5］LIU Yuan，MO Jianhua，TAO Meixia.QoS－aware transmission policies for OFDM bidirectional decode－and－forward relaying［J］.IEEE Trans.Wireless Communications，2013，12(5):2206－2216.

［6］LIU Yinjun，CUI Qimei，FU Ting，et al.Energy－efficient resource allocation for two－way multiple relay OFDM system［C］//Proc.2013 IEEE Vehicular Technology Conference.［S.l.］:IEEE Press，2013:1－5.

［7］WANG Kangping，HUANG Lan，ZHOU Chunguang，et al.Particle swarm optimization for traveling salesman problem［C］//Proc.2003 International Conference on Machine Learning and Cybernetics.［S.l.］:IEEE Press，2003:1583－1585.

［8］EUSUFF M，LANSEY K，PASHA F. Shuffled frog－leaping algorithm:a memetic meta－heuristic for discrete optimization［J］.Engineering Optimization，2006，38(2):129－154.

［9］BABAK A，MOHAMMAD F，ALI M.Application of shuffled frogleaping algorithm on clustering［J］.The International Journal of Advanced Manufacturing Technology，2009，45(1/2):199－209.