权证定价模型及影响因素探讨

（潍坊科技学院 山东寿光262700）

一、有关权证定价研究回顾

随着权证交易的迅速发展，学术界对权证的研究也越来越重视。权证的研究角度很多，在此，只选取权证价格的影响因素和权证与标的证券市场关系的研究进行综述。由于权证是依赖于标的证券发行的衍生证券，因此权证的价格必然要受到标的证券价格的影响，这一点从B-S模型中就能看得出来。认购权证与标的证券的价格成正比，认沽权证与标的证券价格成反比，很多学者对这一规律进行了实证研究。

1973年，Fiseher Black和 Myron Scholes发表了“期权定价和公司财务（The Pricing of Options and Corporate Liability）一文，提出了举世闻名的BS模型，为期权市场的发展扫清了诸多疑惑，随后，很多学者在此基础上进行了更深入的研究，对模型进行了改进，使其更符合客观事实；R.F.Engle率先将GARCH过程应用于权证定价，由GARCH模型估计标的股价波动率，带入B-S模型求得权证的价格。F.Sinkey和R.E.Miles第一次使用B-S模型对权证定价做了研究。E.S.Sehwartz使用数值计算方法对美国电报电话公司 （AT&T）1970-1975年之间发行的权证进行了估价。F.Noreen和 M.Volfson，M.Ferri，J.Kremer 和 H.Obethelman，以及 B.Lairterbacl和 P.Schizltz，使用不同的样本标准，比较了B-S模型和其他波动率弹性恒定的期权定价模型在对权证定价时的能力及表现。R.Kremer和O.Roenfeldt也首次将跳跃扩散模型应用到权证定价当中。

二、权证B-S定价模型

从期权诞生之日起，期权定价就成为了困扰人们的一个难题，不管是发行者还是投资者都不能给期权一个公允的价格，这种情形也严重制约了期权交易的发展。直到20世纪70年代，诞生了著名的权证定价模型。该模型是Fiseher Black和Myron Scholes于1973年首次提出的，该模型在一系列严格的假设条件下，通过严密的数学推导和论证提出了后来被称为“Black-Scholes模型”的期权定价模型（以下简称为B-S模型），成为期权定价理论研究中具有划时代意义的里程碑成果，从此期权定价有了较为科学的参考依据。

B-S模型以欧式看涨期权为研究对象，提出了如下假设：（1）股价变动呈对数正态分布，其期望值与方差一定；（2）交易成本和税率为零，所有证券无限可分；（3）期权有效期（T）内无股息分配；（4）证券交易为连续性交易，不存在无风险套利机会；（5）投资者可以无风险利率进行借贷；（6）无风险利率r恒定。

在以上假设的基础上，提出了欧式看涨期权的价格公式：

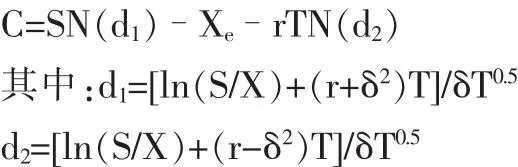
该模型的中心思想是在已知股票价格未来分布的假设下，可以用股票和一个无风险债券组合动态复制期权的收益进行避险，而期权的价格就等于动态复制所需的成本。这一定价模型现已成为交易商们所普遍使用的一个定价工具，极大地推动了衍生产品市场的发展。由于其严密的逻辑、形式上的优美及计算上的简单，B-S模型在实践应用方面被广泛采用，是权证定价应用的著名模型。但其理论本身涉及一些与实际环境不相吻合的假设，导致B-S模型价格与实际期权的市场价格经常有很大的差距。因此，对于其中标的证券价格服从几何布朗运动、波动率为常数的假设，学者们提出了多种修正，推广了建模方法。

三、权证B-S期权定价推广模型

为了使B-S定价模型具有更广泛的现实应用性，很多学者通过放松假设条件，对B-S模型进行了修正和推广。Engle提出的自回归条件异方差 （ARCH）模型成功地模拟了随时间变化的方差模型。该模型针对股票价格波动率聚类效应，假定收益率残差服从一个条件正态分布，条件期望为零，条件方差为以前若干几期收益率误差平方的函数。ARCH模型将方差和条件方差区分开来，并让条件方差作为过去误差的函数而变化，从而为解决异方差问题提供了新的途径。Bollerslev在ARCH模型中引入无穷期误差项，得到广义自回归条件异方差（GARCH）模型。GARCH模型较好地解决了ARCH模型在实际应用中待估参数较多的问题，特别适合于对金融时间系列数据的波动性和相关性进行建模，估计或预测波动性和相关性。Kuwahara&Marsh在使用GARCH模型对认股权证定价进行实证研究中发现，该模型对价内认股权证的定价准确度要优于经典B-S模型。尽管GARCH模型在描述金融时间序列的波动率上有诸多优势，但能够反映连续时间序列波动率的SV模型更受金融研究者青睐。该模型在波动率方程中引入了一个新的随机变量，提高了对长期波动率预测的准确性。

我国的香港和台湾地区权证市场起步早，发展快，因此针对这两个市场的研究较丰富，其中比较有代表性的著作有：陈松男证明B-S模型计算出的权证价格只是一个定价的参考值，时常背离其真实价值，因此存在应用的局限性。该研究利用实务观点并提供新的理论基础说明如何修正B-S模型理论，以改进其在实际应用中的效率，降低权证风险，并提高超额收益，具有较强的实际指导意义。陈信华选择我国台湾证券商最早发行的4只认购权证作为研究对象，探讨了台湾券商发行权证的发行定价、市场价格与理论价格的关系。其研究结果如下：由于证券商的权证发行价格制定采用高波动率政策，造成定价高于B-S模型与二项式理论价格的情况时有发生。

四、认购权证价格的影响因素

虽然B-S模型和二项式理论给出了权证定价的表达公式，但是在实际的交易中，权证价格还要受到诸多因素的影响。

（一）标的证券的价格

权证作为金融衍生产品，标的资产可以为个股、一篮子股票、指数以及其他衍生产品。所以说，从短期来看，标的证券的价格走势将直接影响到权证的交易价格。对于认购权证来说，发行时标的证券的价格越高，认购权证的发行价格也越高。同样的道理，认沽权证标的证券价格越高，权证发行时的价格就越低。通过B-S模型可以看出，标的证券价格是权证定价的重要影响因素。张成虎等对中国权证与其标的证券之间的价格协整关系进行实证研究，研究表明，从长期来看，认购权证价格与标的证券价格都是存在单位根的非平稳序列，都是一阶单整的。研究结果还显示不同的认购权证价格与其标的证券价格的均衡关系存在一定的差异。这与前人的研究成果是基本吻合的。

（二）权证有效期

在股票市场牛市环境下，权证离行权到期日时间越长，认购权证成为价内权证的可能性就越大，所以它的价格也相应的越高；随着到期日的趋近，认购权证成为这种价内权证的可能性越小，则它的交易价格也会逐渐趋向稳定。在股票市场牛市作用下，认沽权证离行权到期日时间越长，成为价外权证的可能性就越大，所以它的价格趋向下降；认沽权证到期时基本上都属于价外权证，没有行权可能。

（三）权证行权价格

权证的核心价值在于对标的证券价格的预期，价内权证具有一定的内在价值，而价外权证没有内在价值。价内权证行权价与标的股票价格的差距越大，那么权证提供的套利空间就越大，权证的内在价值就越高，所以权证的发行价格或交易价格就可能越高。认购权证所约定的行使价格越高，投资者到期行使认购权利时，行权价跟标的证券价格的差额越小，权证的收益率就越低，所以权证的发行价格或交易价格都会较低。认沽权证所约定的行权价格越低，投资者到期行使认沽权利时，行权价与标的证券价格的差额越小，权证的收益率就越低，这样权证的发行价格和交易价格也越低。

此外，根据以上分析的权证的定价模型可以看出，影响权证的因素还有标的证券的波幅、市场利率、标的证券预计派发的股息等。