基于应变路径法的压入管桩单桩挤土位移场的参数影响分析

汪敏，储召军，2，石少卿，2，孙建虎

（1后勤工程学院 军事土木工程系，重庆 401311；2岩土力学与地质环境保护重庆市重点实验室，重庆 401311）

0 引言

《基于应变路径法的压入管桩单桩挤土位移研究》中，作者基于应变路径法和球孔扩张理论[1-4]，结合真实源与虚拟源、真实源与虚拟汇的相互作用，并修正地表面处的附加剪应力和正应力，在小应变假定的前提下推导了开口型压入管桩（简称压入管桩）单桩挤土位移场[5-10]的解析解，得出压入管桩单桩竖向挤土位移场如式（1）所示、水平挤土位移场如式（2）所示。

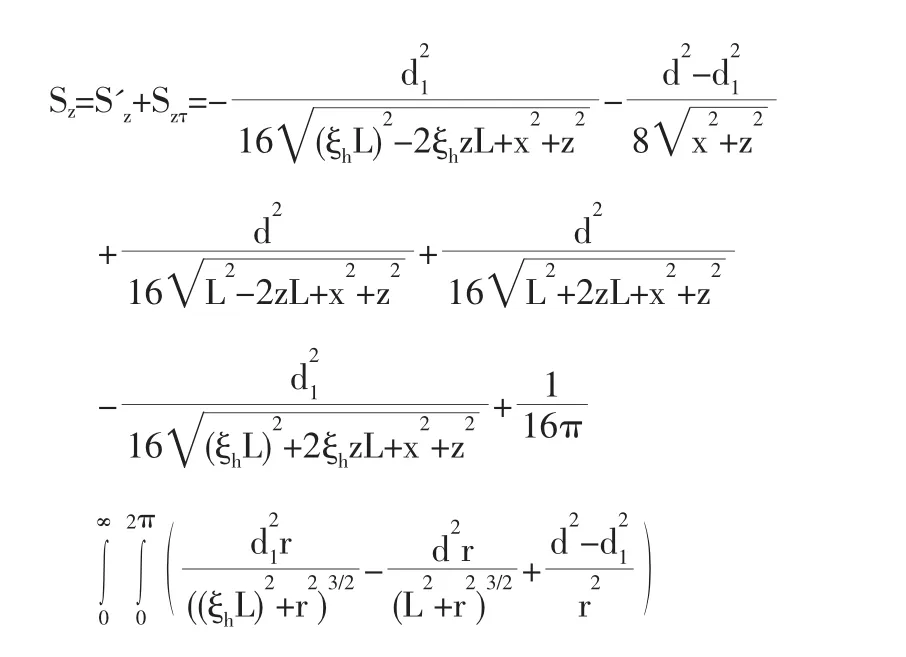
式中：d1、d表示管桩内外径；ξhL表示压桩过程中产生的土塞高度最大值；L表示桩长；x、z分别表示土中任一点P的x轴和z轴坐标。

但从解析解难以直接感受它的变化规律，而通过图形却可以直观形象地感受其内在本质。为了直观反映挤土位移场沿径向和深度方向的变化规律、分析各参数对挤土位移场的影响，本文借助Matlab软件绘制压入管桩单桩挤土位移场在不同深度处和不同径向处的二维曲线图。

分析式（1）与式（2）可知，压入管桩单桩挤土位移场的影响参数主要有：管桩外径d、管桩内径d1、桩长L（即压桩深度）和土塞高度最大值ξhL。为了研究问题的方便，本文将管桩外径d作为基本单位，并引入参数ξr来表征管桩内外径的比值。

1 应变路径法的基本原理

应变路径法是将光滑圆头桩的桩端看成一个点源，压桩时点源沿竖直方向运动，与桩周土体相互作用，而模拟了一个光滑圆头桩的压桩过程。它在忽略地表面边界条件的情况下得到了独立于本构关系的应变场，再由物理方程得到应力。

应变路径法的基本假定为：（1）土体为均匀、不排水、不可压缩且各向同性的无限体，压桩过程稳定；（2）桩尖到达处土体按球形孔扩张，并以一定的速度向下匀速运动；（3）土体变形不考虑本构关系，由不旋转的无粘性理想流体决定；（4）不计土体自重。

2 桩长对压入管桩单桩挤土位移的影响

不同桩长情况下各算例参数如表1所示。

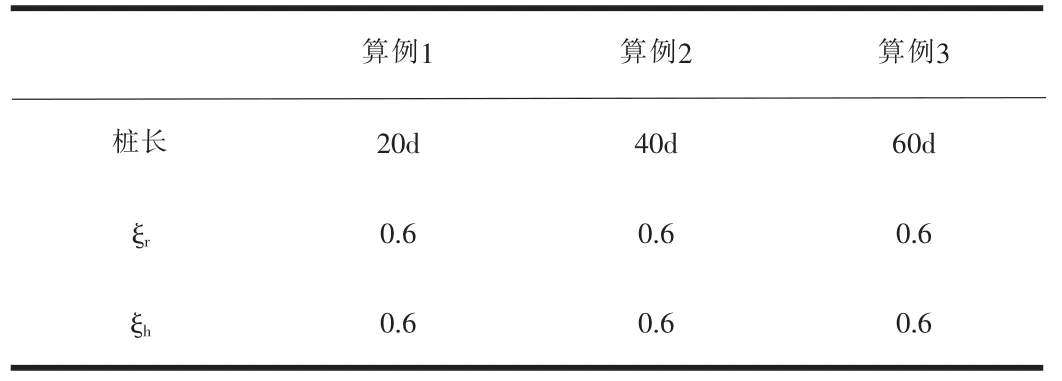
表1 不同桩长情况下的算例参数

2.1 竖向挤土位移的变化规律分析

当深度z为定值0、L时，改变压入管桩桩长，压桩所致的竖向挤土位移在径向的分布规律如图1所示。由图1可知，其分布规律趋于一致：（1）竖向挤土位移随径向距离的增大而逐渐减小；（2）地表土体的竖向挤土位移方向向上，表现为隆起；桩端处土体的竖向挤土位移方向向下，表现为沉降。

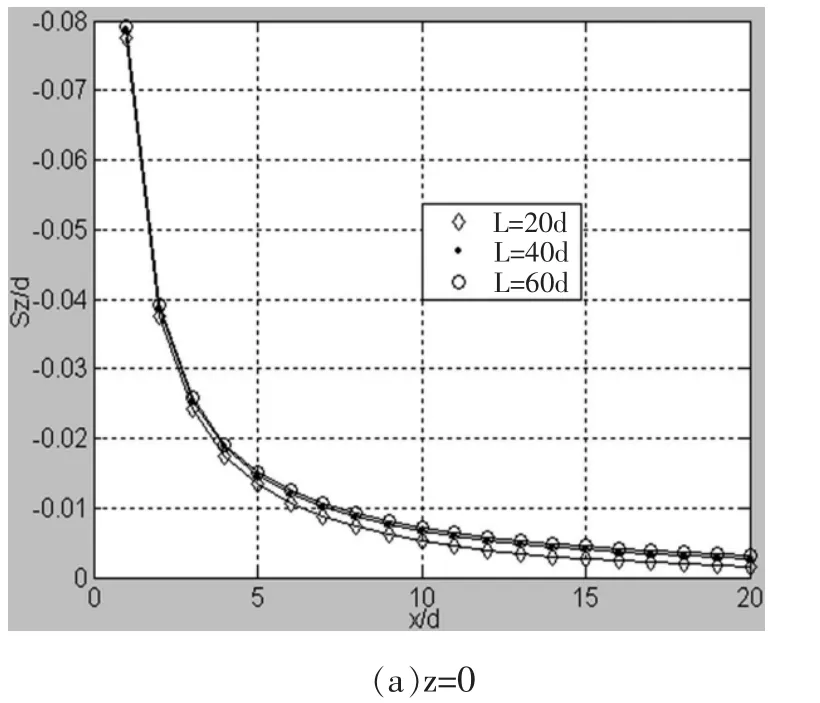
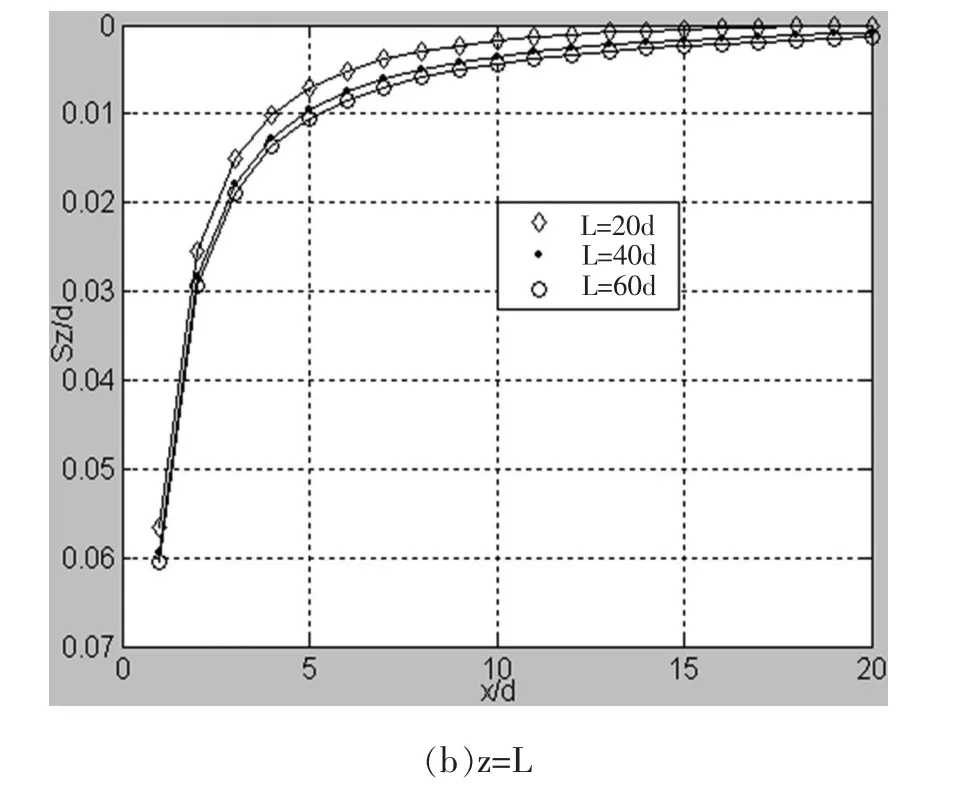
图1 不同桩长竖向挤土位移在不同深度沿径向的分布规律

当径向距离x为定值5d、15d时，改变压入管桩桩长，压桩所致的竖向挤土位移在深度方向的分布规律如图2所示。由图2可知，其分布规律趋于一致：（1）当深度增大时，竖向挤土位移逐渐由隆起变为沉降；（2）z=L深度处土体的沉降量最大，z=0处土体即地表土体隆起量最大。但径向距离为5d时，不同桩长情况下竖向挤土位移的变化过程有所差异：桩长为20d时，向上的竖向挤土位移沿深度始终逐渐减小；桩长为40d和60d时，向上的竖向挤土位移沿深度先逐渐减小再逐渐增大，随后又逐渐减小。

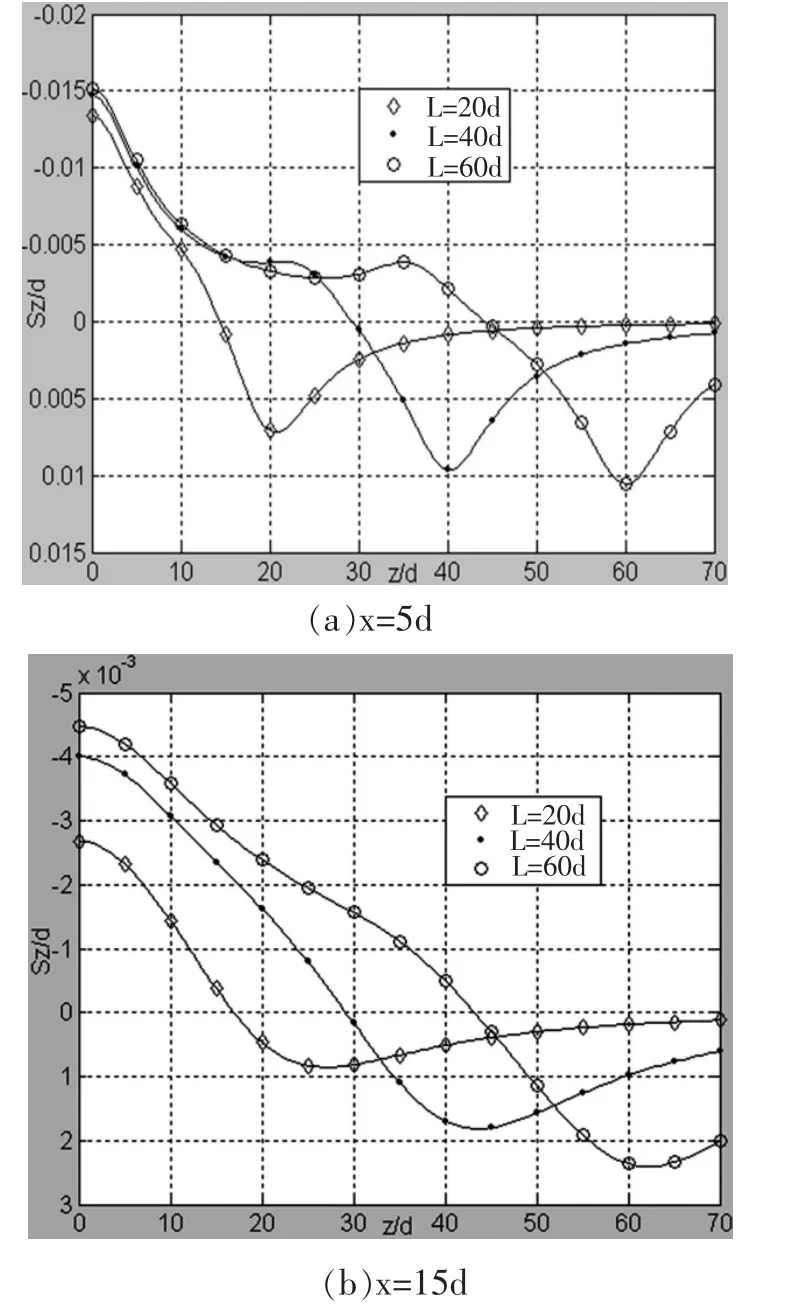
图2 不同桩长竖向挤土位移在不同径向沿深度的分布规律

2.2 水平挤土位移的变化规律分析

当深度z为定值0、L时，改变压入管桩桩长，压桩所致的水平挤土位移在径向的分布规律如图3所示。由图3可知，其分布规律趋于一致：当径向距离增大时，水平挤土位移逐渐减小。

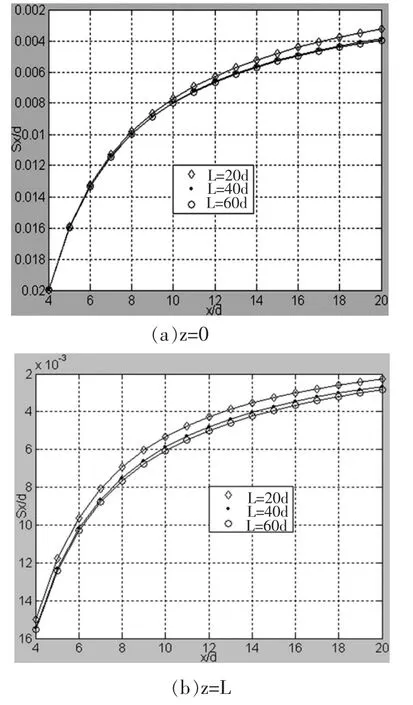
图3 不同桩长水平挤土位移在不同深度沿径向的分布规律

当径向距离x为定值5d、15d时，改变压入管桩桩长，压桩所致的水平挤土位移在深度方向的分布规律如图4所示。径向距离为5d时，其分布规律趋于一致：水平挤土位移随深度的增大先逐渐增大再逐渐减小，3L/4深度处达到最大。径向距离为15d时，分布规律有所差异：桩长为40d和60d时，分布规律同径向距离为5d时；桩长为20d时，当深度增大时，水平挤土位移逐渐减小。

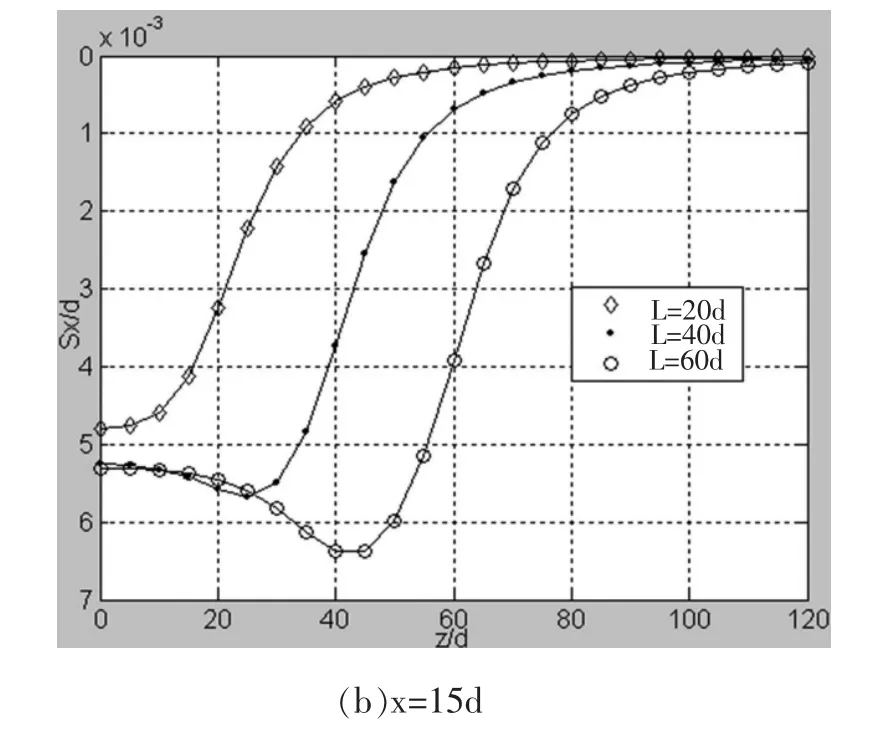
图4 不同桩长水平挤土位移在不同径向沿深度的分布规律

比较三种桩长情况下相同位置土体的竖向和水平挤土位移的大小，由大至小排列时桩长依次为：60d、40d、20d，表明相同管桩内外径和ξh时，桩越长，压入管桩压桩所致的竖向和水平挤土位移都越大。

3 ξr对压入管桩单桩挤土位移的影响

不同ξr情况下各算例参数如表2所示。

表2 不同ξr情况下的算例参数

3.1 竖向挤土位移的变化规律分析

当深度z为定值0、L时，改变压入管桩内外径的比值ξr，压桩所致的竖向挤土位移在径向的分布规律如图5所示。由图5可知，其分布规律趋于一致：（1）竖向挤土位移随径向距离的增大而逐渐减小；（2）地表土体的竖向挤土位移方向向上，表现为隆起；桩端处土体的竖向挤土位移方向向下，表现为沉降。

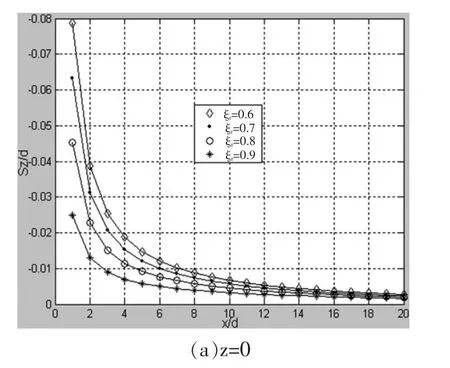
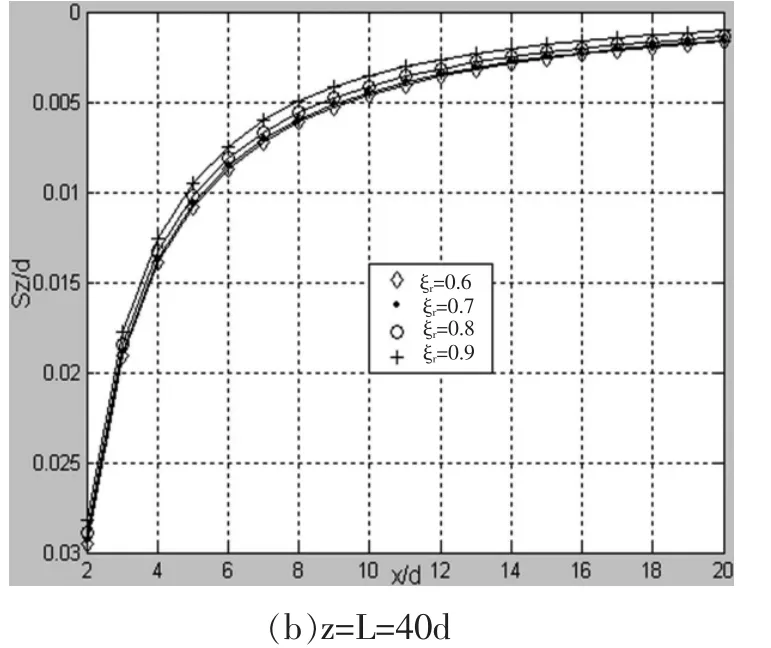
图5 不同ξr竖向挤土位移在不同深度沿径向的分布规律

当径向距离x为定值5d、15d时，改变压入管桩内外径的比值ξr，压桩所致的竖向挤土位移在深度方向的分布规律如图6所示。由图6可知，其分布规律基本一致：当深度增大时，竖向挤土位移逐渐由隆起变为沉降，于z=L深度处的沉降量最大。但径向距离为5d时，不同ξr的竖向挤土位移的变化过程有所差异：ξr为0.6时，向上的竖向挤土位移沿深度始终逐渐减小；ξr为0.7、0.8和0.9时，向上的竖向挤土位移沿深度先逐渐减小再逐渐增大，随后又逐渐减小。

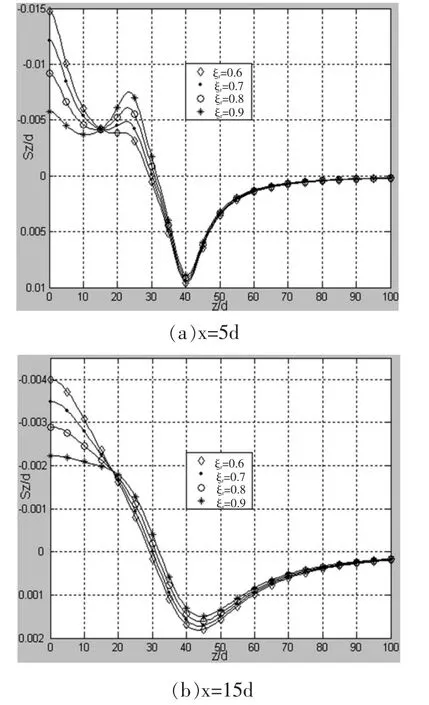
图6 不同ξr竖向挤土位移在不同径向沿深度的分布规律

3.2 水平挤土位移的变化规律分析

当深度z为定值0、L时，改变压入管桩内外径的比值ξr，压桩所致的水平挤土位移在径向的分布规律如图7所示。由图7可知，其分布规律趋于一致：当径向距离增大时，水平挤土位移逐渐减小。

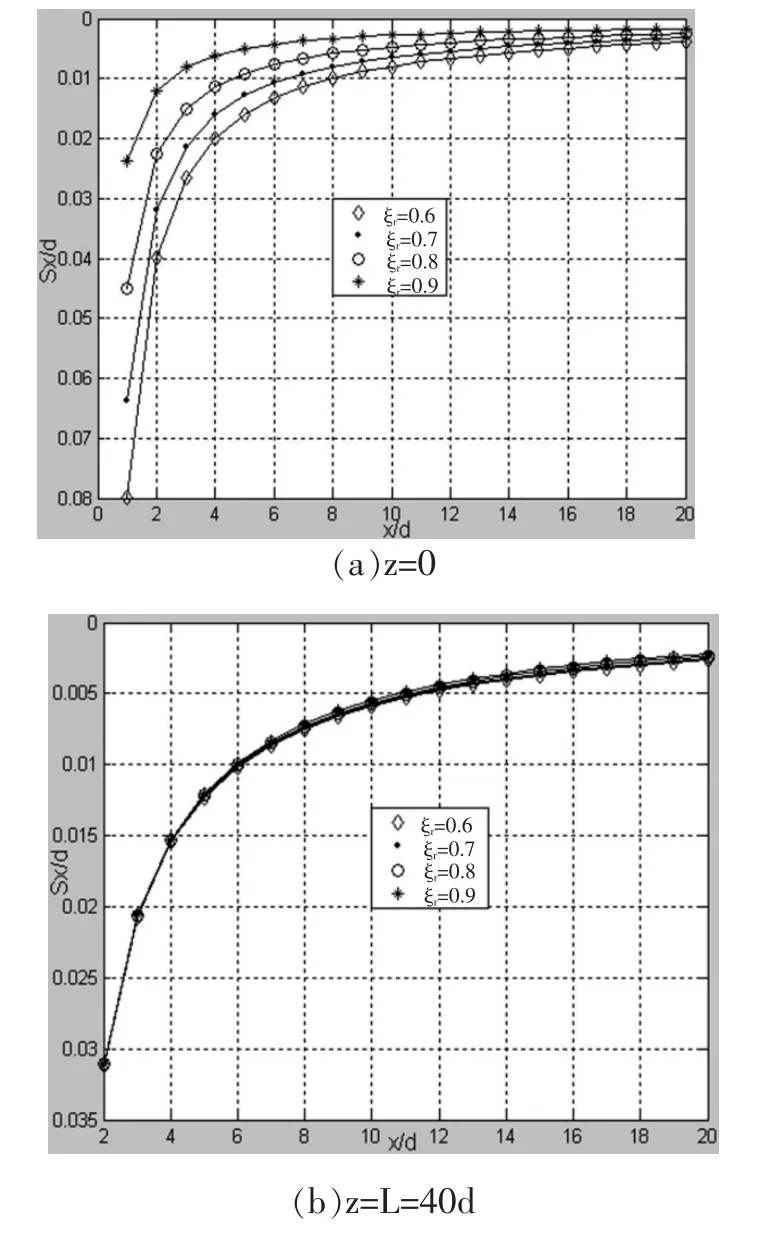
图7 不同ξr水平挤土位移在不同深度沿径向的分布规律

当径向距离x为定值5d、15d时，改变压入管桩内外径的比值ξr，压桩所致的水平挤土位移在深度方向的分布规律如图8所示。由图8可知，其分布规律趋于一致：当深度逐渐增大时，水平挤土位移先逐渐增大再逐渐减小，3L/4深度处达到最大。

图8 不同ξr水平挤土位移在不同径向沿深度的分布规律

比较四种ξr种情况下相同位置土体的竖向和水平挤土位移的大小，由大至小排列时ξr依次为：0.6、0.7、0.8、0.9，表明相同管桩外径、ξh和桩长时，ξr越大即管桩内径越大，管壁越薄，压入管桩压桩所致的竖向和水平挤土位移都越小。

4 ξh对挤土位移场的影响

不同ξh况下各算例参数如表3所示。

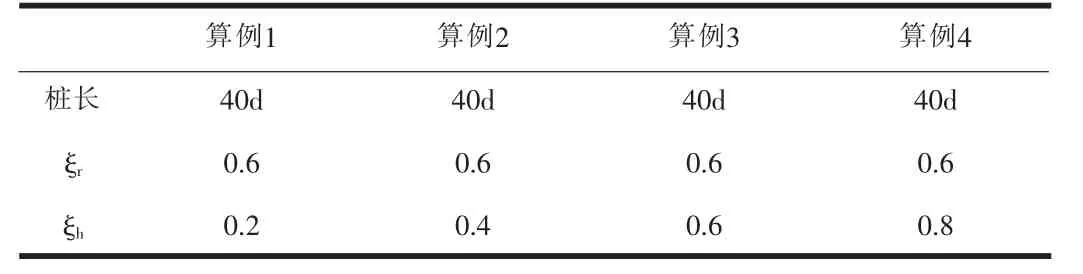
表3 不同ξh情况下的算例参数

4.1 竖向挤土位移的变化规律分析

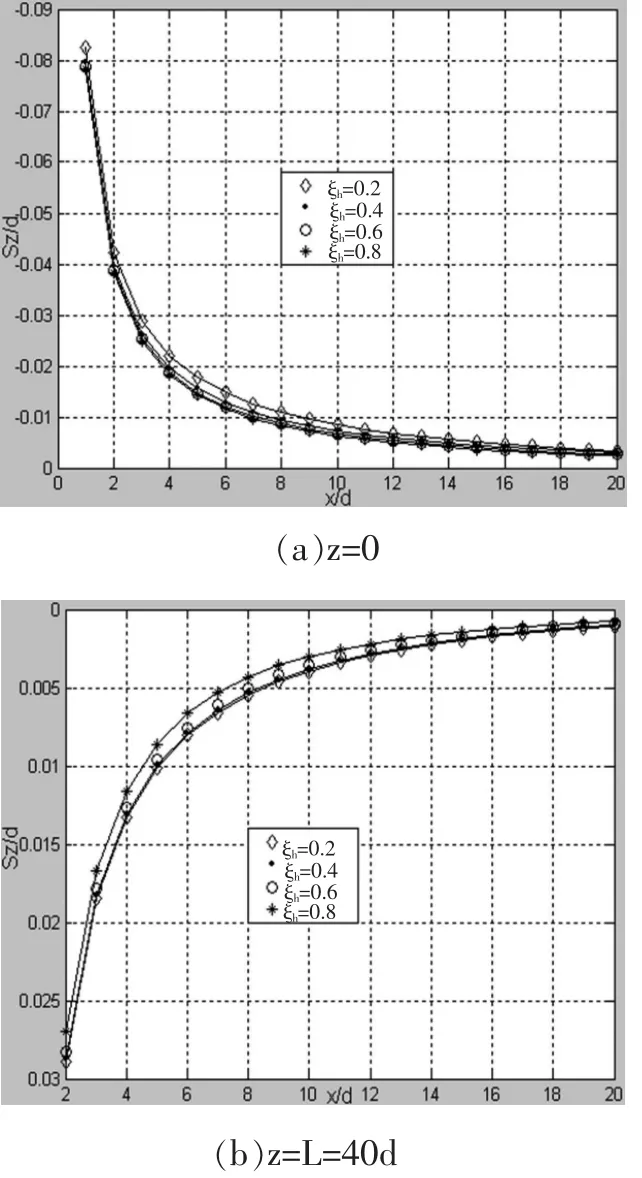
图9 不同ξh竖向挤土位移在不同深度沿径向的分布规律

当深度z为定值0、L时，改变土塞高度最大值与桩长的比值ξr，压入管桩压桩所致的竖向挤土位移在径向的分布规律如图9所示。由图9可知，其分布规律趋于一致：（1）竖向挤土位移随径向距离的增大而逐渐减小；（2）地表土体的竖向挤土位移方向向上，表现为隆起；桩端处土体的竖向挤土位移方向向下，表现为沉降。

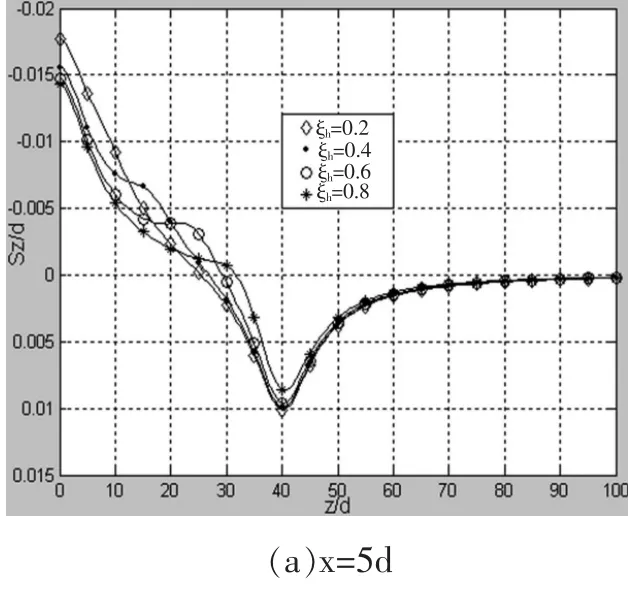
当径向距离x为定值5d、15d时， 改变土塞高度最大值与桩长的比值ξr，压入管桩压桩所致的竖向挤土位移在深度方向的分布规律如图10所示。由图10可知，其分布规律基本一致：（1）当深度逐渐增大时，竖向挤土位移逐渐由隆起变为沉降；（2）z=L深度处土体的沉降量最大，z=0处土体即地表土体的隆起量最大。

4.2 水平挤土位移的变化规律分析

当深度z为定值0、L时， 改变土塞高度最大值与桩长的比值ξr，压入管桩压桩所致的水平挤土位移在径向的分布规律如图11所示。由图11可知，其分布规律趋于一致：当径向距离增大时，水平挤土位移逐渐减小。

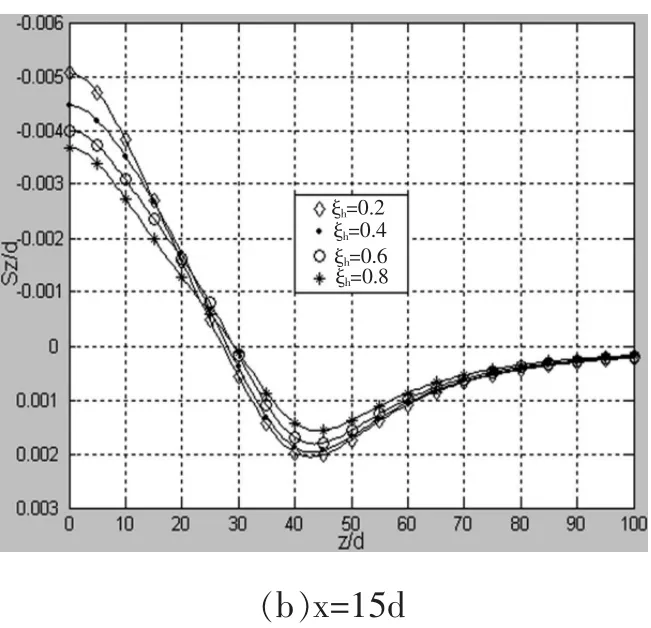
图10 不同ξh竖向挤土位移在不同径向沿深度的分布规律

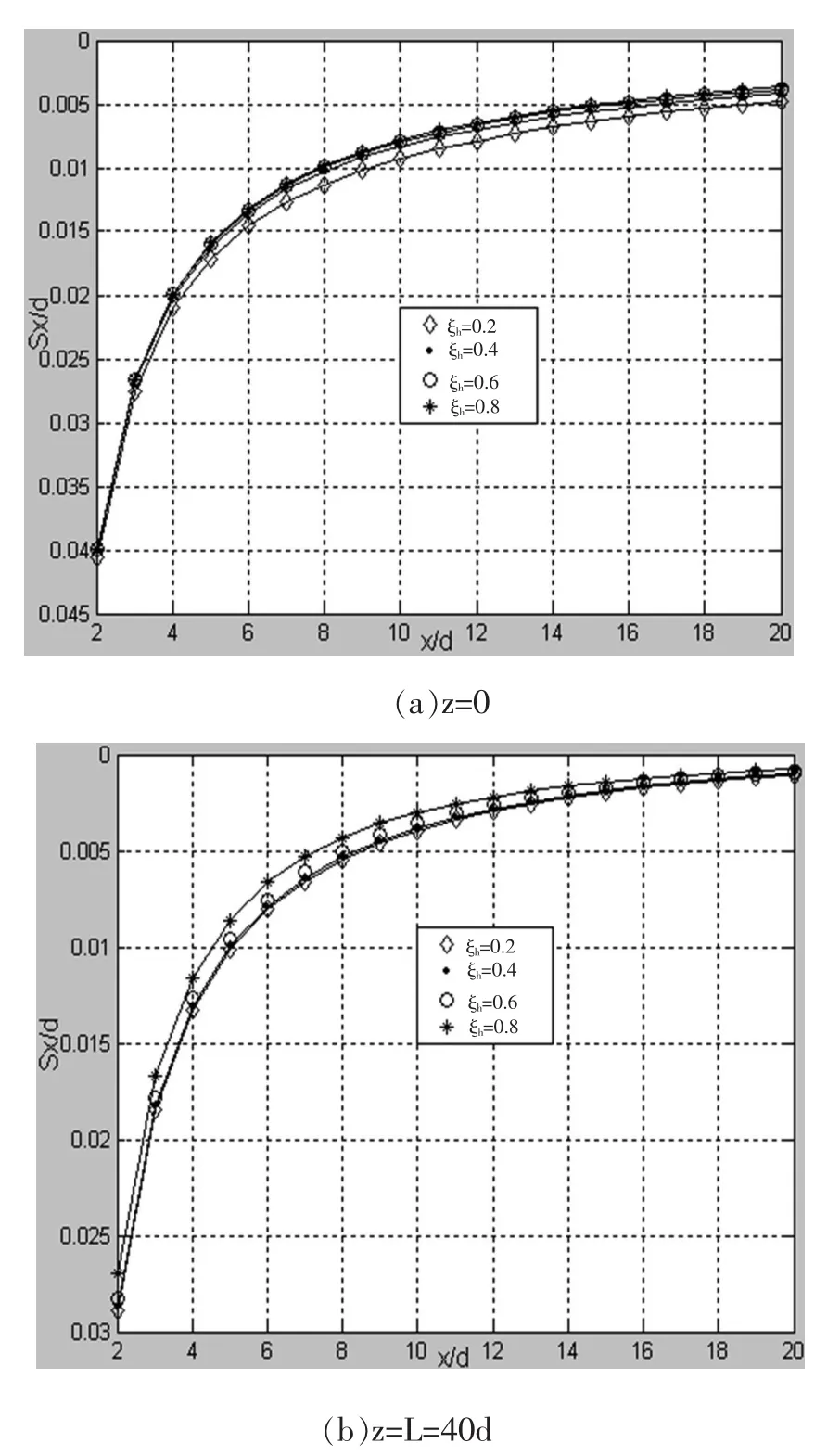
图11 不同ξh水平挤土位移在不同深度沿径向的分布规律

当径向距离x为定值5d、15d时，改变土塞高度最大值与桩长的比值ξr，压入管桩压桩所致的水平挤土位移在深度方向的分布规律如图12所示。径向距离为5d时，其分布规律趋于一致：当深度逐渐增大时，水平挤土位移先逐渐增大再逐渐减小。但水平挤土位移达到最大值的位置不同，ξh越大，达到最大值的深度越大。径向距离为15d时，其分布规律有所差异：ξh为0.2、0.4和0.6时，分布规律同径向距离为5d时；ξh为0.8时，当深度逐渐增大时，水平挤土位移逐渐减小。

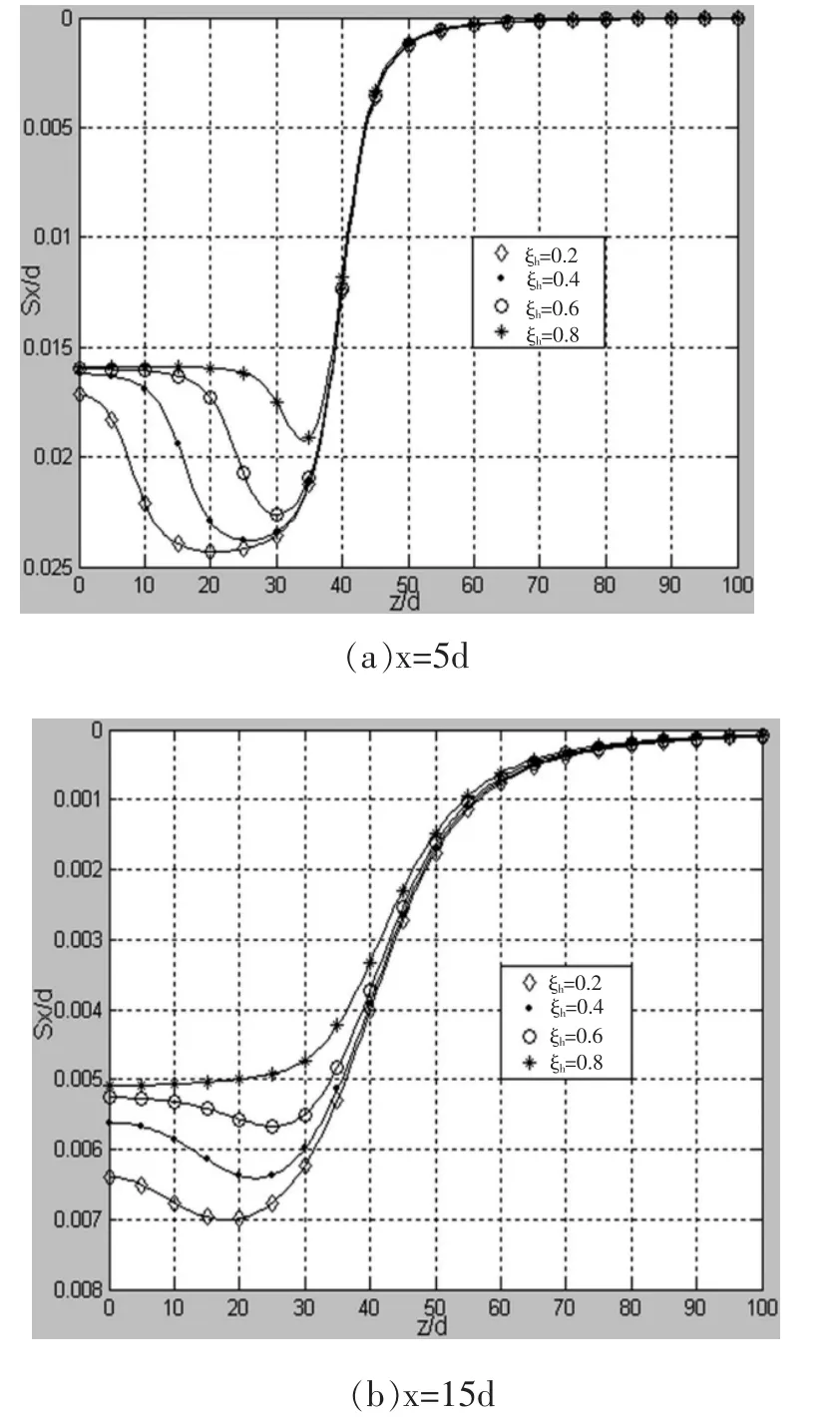
图12 不同ξh水平挤土位移在不同径向沿深度的分布规律

比较四种ξh情况下相同位置土体的竖向和水平挤土位移的大小，由大至小排列时ξh依次为：0.2、0.4、0.6、0.8，表明相同管桩内外径和桩长时，ξh越大即土塞高度最大值越大，压入管桩压桩所致的竖向和水平挤土位移都越小。

5 结语

针对 《基于应变路径法的压入管桩单桩挤土位移研究》中所得的压入管桩单桩挤土位移场的解析解，分析了不同管桩内外径d1与d、桩长L和土塞效应系数ξh情况下压桩产生的挤土位移，得出了如下结论，并为下一步压入管桩的优化设计奠定基础：

（1）改变压入管桩桩长，压桩所致的竖向和水平挤土位移在不同径向距离处沿深度方向和不同深度处沿径向的分布规律都趋于一致。数值上，桩长的变化对压入管桩压桩所致的挤土位移影响较小。相同管桩内外径和ξh（土塞高度最大值与桩长的比值）时，桩越长，压桩产生的挤土位移越大。

（2）改变压入管桩内外径比值ξr，压桩所致的竖向挤土位移在不同径向距离处沿深度方向和不同深度处沿径向的分布规律都趋于一致；压桩所致的水平挤土位移在不同深度处沿径向的分布规律趋于一致，不同径向距离处沿深度方向的分布规律有所差异。数值上，ξr的变化对压桩产生的挤土位移产生较大的影响。相同管桩外径、ξh和桩长时，ξr越大，压桩产生的挤土位移越小。

（3）改变土塞高度最大值与桩长的比值ξr，压入管桩压桩所致的竖向挤土位移在不同径向距离处沿深度方向和不同深度处沿径向的分布规律都趋于一致；压桩所致的水平挤土位移在不同深度处沿径向的分布规律趋于一致，在不同径向距离处沿深度方向的分布规律有所差异。数值上，ξh的变化对压桩产生的挤土位移产生较小的影响。相同管桩内外径和桩长时，ξh越大，压桩产生的挤土位移越小。

[1]Baligh， M.M.Strain path method[J].Geotech.Eng， ASCE，1985，111:1108-1136.

[2]David White， Tim Finlay， Malcolm Bolton， Grant Bearss.Press-in piling:Ground vibration and noise during pile installation[J].Proceedings of the International Deep Foundations Congress.Orlando，USA.ASCE Special Publication:363-371.

[3]潘林有.利用园孔扩张理论分析静压桩挤土效应[J].地下空间， 1999， 19（3）:174-177.

[4]Sagaseta，C.Analysis of undrained soil deformation due to ground loss[J].Geotechnique， 1987， 37（3）:301-320.

[5]罗战友，童健儿，龚晓南.预钻孔及管桩情况下的压桩挤土效应研究[J].地基处理， 2005， 16（1）:3-8.

[6]Mabsout， M.E.， Teese， L.C， and Tassoulas， J.L.Study of pile driving by finite element method[J].Joumal of Geotechnical Engineering，ASCE，1995，121:535-543.

[7]刘裕华，陈征宙，彭志军，等.应用圆孔柱扩张理论对预制管桩的挤土效应分析[J].岩土力学，2007，28（10）:2167-2172.

[8]肖昭然，张昭，杜明芳.饱和土体小孔扩张问题的弹塑性解析解[J].岩土力学， 2004， 25（9）:1373-1378.

[9]储召军，石少卿，陈怀庆，等.土体泊松比对压入管桩单桩挤土位移场的影响[J].后勤工程学院学报，2013，29（3）:1-7.

[10]储召军，陆新，石少卿，等.压入管桩压桩所致挤土位移的数值模拟[J].后勤工程学院学报，2013，29（2）:1-7.