基于轮球自平衡机构的机器人设计

毛丽民，卢振利，朱培逸，刘叔军

（常熟理工学院 电气与自动化工程学院，常熟 215500）

0 引言

自平衡机器人的概念源于二十世纪八十年代，基于倒立摆的模型，其系统是一个非线性、强耦合、多变量和自然不稳定的系统[1]。

轮球自平衡机构组成的机器人通过自身的平衡调节器，使其在球上近似平稳的站立，实现动态平衡。球与地面有一个微小的接触点，和一般的多轮车相比，单足平衡机器人灵活性更好。可以应用到大型购物中心、际会议或展览场所等领域，根据不同的应用场合加入各类不同功能，例如加入避障、定位和网络访问控制，实现物体运送的功能

1 机器人机构及自平衡原理

1.1 机器人机构

机器人结构主要由主控制器、主框架、蓝牙模块、陀螺仪模块、各类模块等组成。机器人总高度为28cm；身长25cm，宽25cm；全向轮直径5cm；球直径18cm。机器人模型如图1所示。

图1中数字代表：1为构架，2为电机驱动，3为主控制器独立电源，4为OLED，5为主控制器，6为蓝牙模块，7为24V电源8为稳压模块，9为总开关，10为直流电机，11为全向轮。

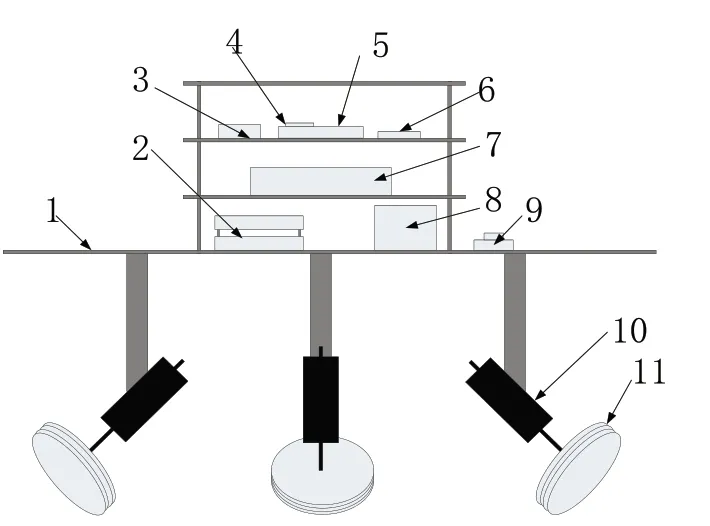
图1 轮球自平衡机器人模型（无球部分机构）

根据上述模型，设计完成第一代轮球自平衡机器人（无球部分机构）样机如图2所示。

图2 轮球自平衡机器人样机

1.2 轮球移动机器人自平衡原理

该机器人驱动部分是通过三个电机驱动的轮子，组成一个平面，彼此相差120度。该部分与球组成一个移动机构，该球直径应该满足R球＞α*R万向轮组, α为实验安全系数，这里取1.414。

在机器人维持平衡过程中，由于变化的角度相对较小，把机器人的运动系统近似的看成平面，建立的运动模型如图3所示。

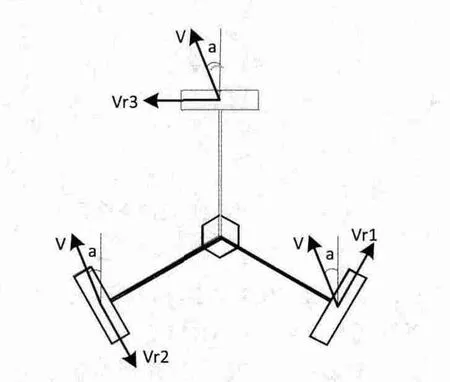
图3 运动模型

模型中三个电机两两相隔120度，Vr是万向轮运动正方向的运动速度，V是任意的某一方向的运动速度，a是V和0度线间的夹角，通过调节三个电机的转速和正反转合成V，由于本模型的建立是在刚性物体的基础上，得到以下公式：

通过上述的数学模型，实现机器人在保持自平衡基础上的二维运动。Vr1，Vr2，Vr3分别代表万向轮系统中3个轮的转速。

2 基于多传感器设计机器人控制系统

本文设计的单足自平衡机器人，以STM32为控制核心，以MPU-9150实现姿态检测，得到角速度和角加速度，经过卡尔曼数据融合得到真实的姿态值。通过PID算法对实时姿态值处理得到PWM波，对以F2807S为开关管的H桥电机驱动进行控制，以三号足球为机器人的单足，实现机器人在足球上保持平衡。利用OLED显示屏实现人机交互，通过蓝牙模块进行通讯。机器人多传感器控制系统框图如图4所示。

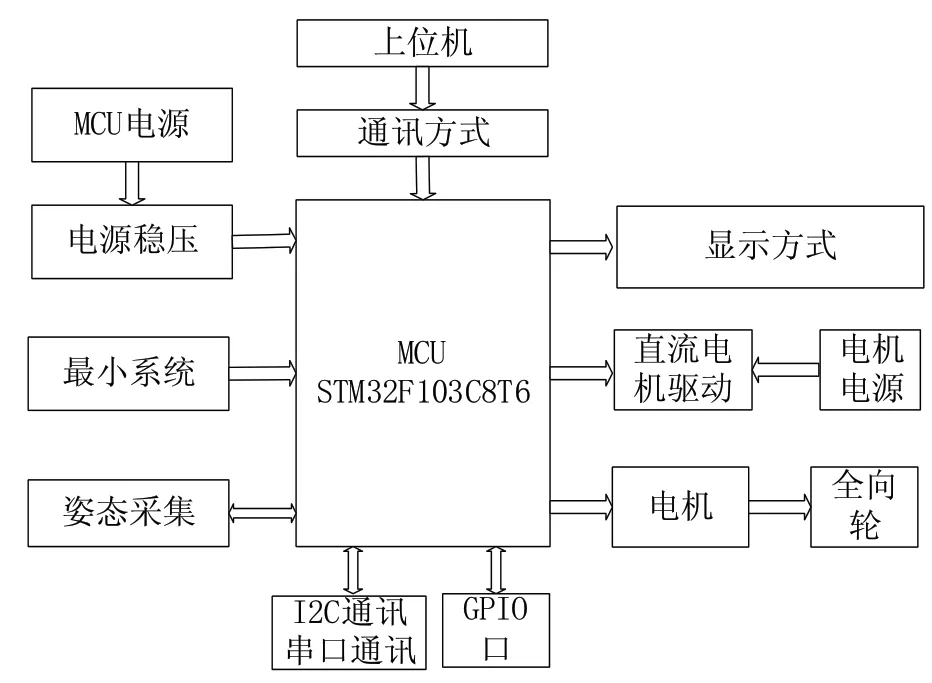
图4 机器人多传感器控制系统框图

3 机器人多传感器控制系统硬件设计

3.1 系统的供电电路设计

单足自平衡机器人的电源是3.7V的锂电池，选用AMS1117三端稳压器将3.7V电压转成3.3V给单片机供电，如图5所示。

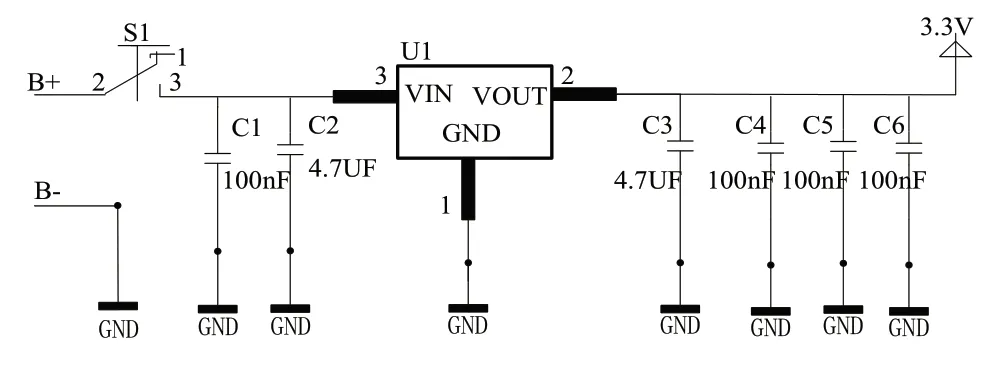
图5 AMS1117-3.3V稳压电路图

3.2 姿态检测电路设计

轮球自平衡移动机器人为保持平衡，需实时采集机器人的姿态值，在本设计选用MPU-9150姿态传感器，通过对加速度值和速度值的处理可得到机器人的姿态值。姿态检测电路如图6所示。

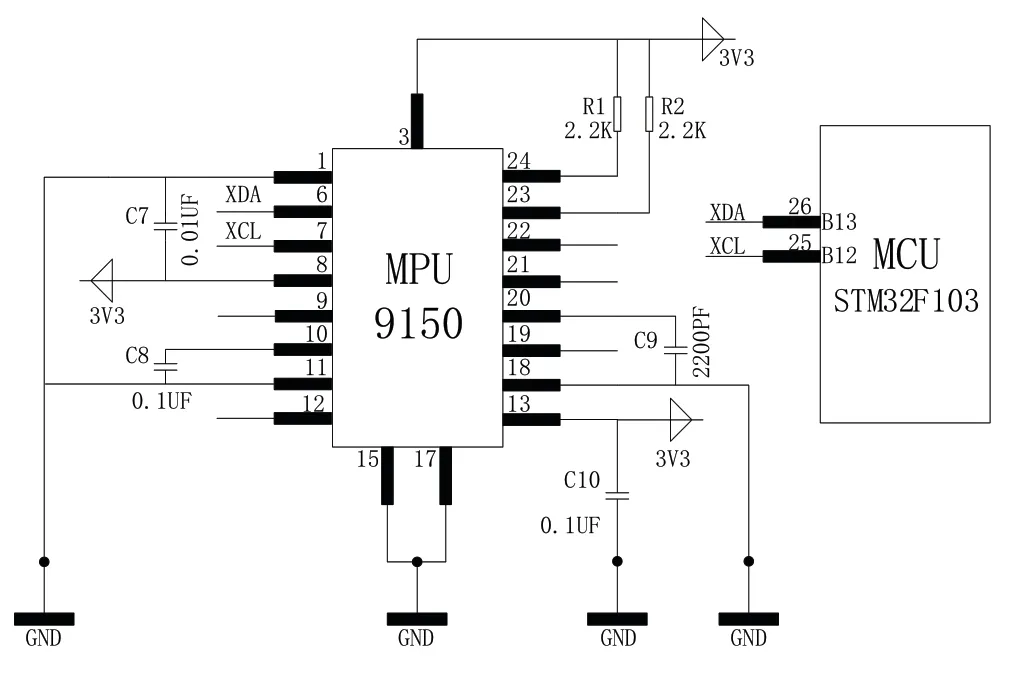
图6 姿态检测电路图

3.3 电机驱动电路设计

本文设计的电机驱动电路是N沟道MOS管全桥电路，主要由控制电路和主电路组成，实现直流电机的加、减速和正反转的功能。

图7为电机驱动信号逻辑电路图，图中控制电路使用与非门逻辑器，控制端口使用0和1来控制电机正反转，PWM波占空比来控制电机转速，达到最优的控制效果。

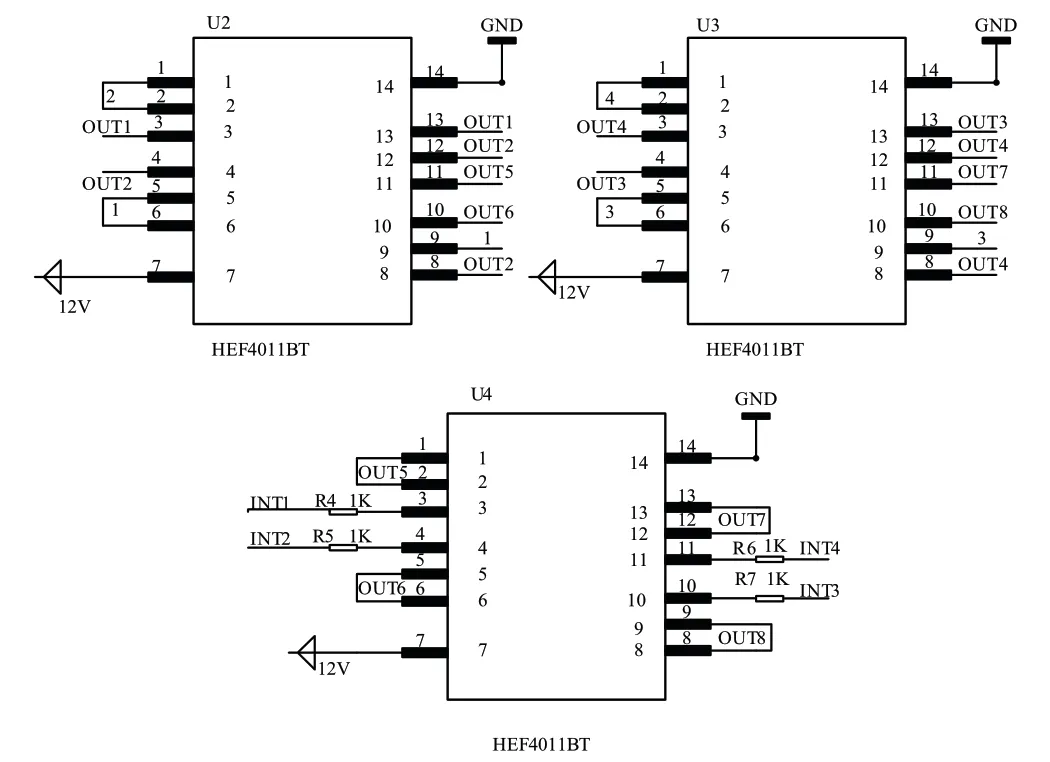
图7 信号逻辑电路图

图8为电机驱动主电路图，图中IRF2807S为MOS管，漏极电流为82A，最大电压为75V。IR2104S是半桥驱动器，使得电路可以无需脉冲变压器驱动，得到所须的工作频率，提高了电路的频率稳定性。

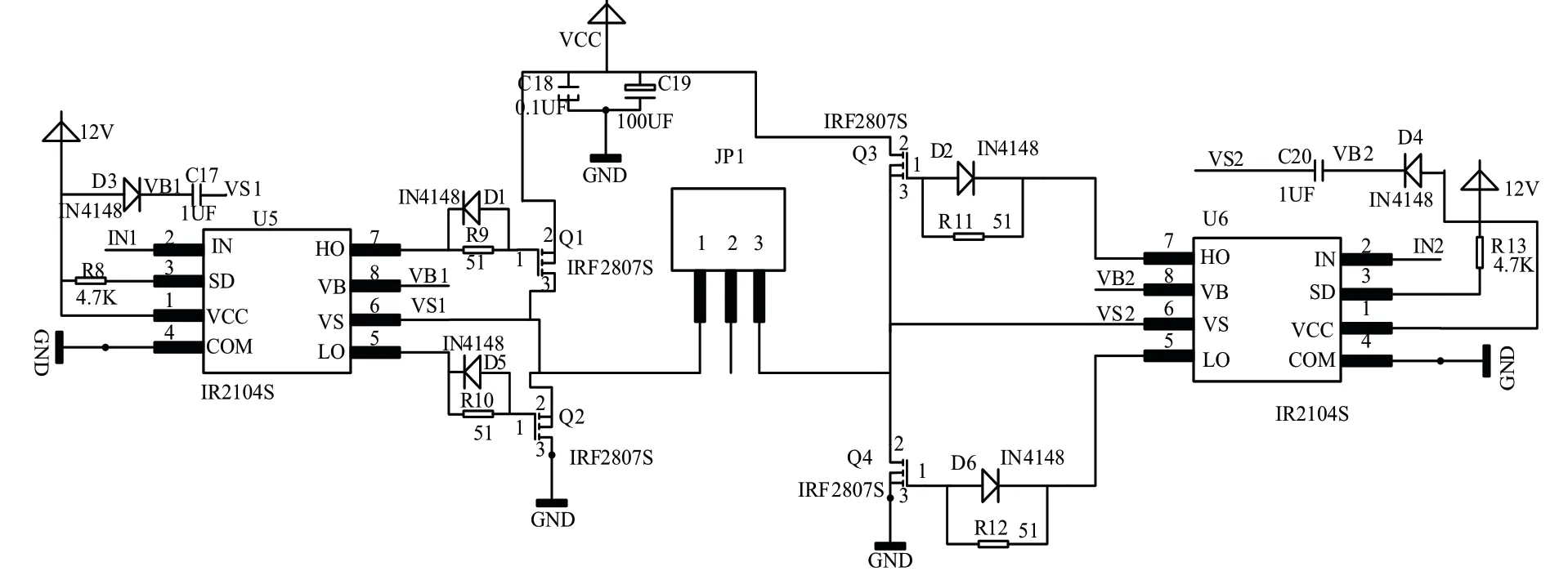
图8 电机驱动主电路图

4 机器人多传感器控制系统软件设计

4.1 姿态检测软件设计

控制器通过I2C传输协议读取姿态传感器中的速度和加速度值，进行处理，得出姿态角（倾斜角和航向角），流程如图12所示。

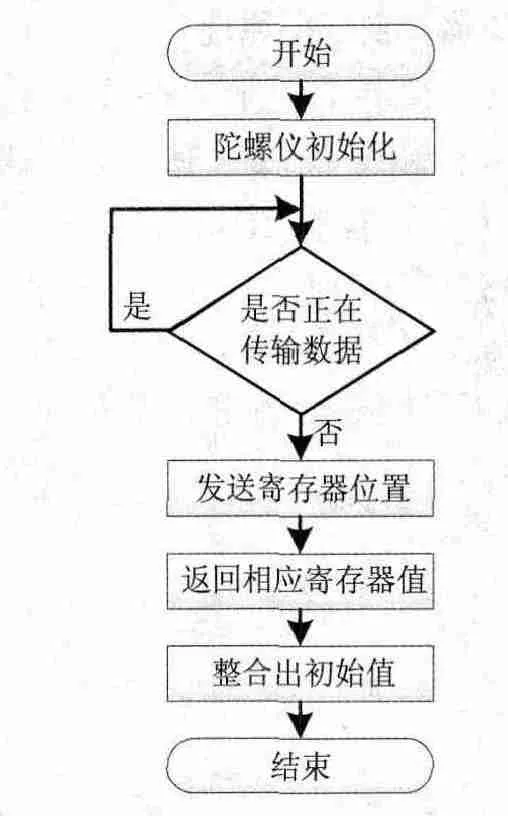
图9 陀螺仪软件设计流程图

图12 单足自平衡机器人调试

姿态传感器程序中包括读取相应寄存器中的值和整个处理得出初始值两个部分，其中BUF[12]是一个用于陀螺仪数据缓存的数组，ACCEL_XOUT_L、ACCEL_YOUT_L、ACCEL_ZOUT_L分别表示X、Y、Z轴的角加速度值得低八位数据；ACCEL_XOUT_H、ACCEL_YOUT_H、ACCEL_ZOUT_H分别表示X、Y、Z轴的角加速度值得高八位数据；GYRO_XOUT_L、GYRO_YOUT_L、GYRO_ZOUT_L分别表示X、Y、Z轴的角速度值得低八位数据；GYRO_XOUT_H、GYRO_YOUT_H、GYRO_ZOUT_H分别表示X、Y、Z轴的角速度值得高八位数据；A_X、A_Y、A_Z为整合处理后的角加速度初始值；G_X、G_Y、G_Z则为整合处理后的角速度初始值。

4.2 基于卡尔曼滤波器设计机器人姿态估计器

卡尔曼滤波器的控制主要有两个方面：预测与更新。在预测时，通过上一时刻状态的判断，计算出实时状态；在更新时，实时观测值使预测阶段取得的测量值最优化，得出最新估计值。卡尔曼滤波步骤如下：

1）先验状态估计：

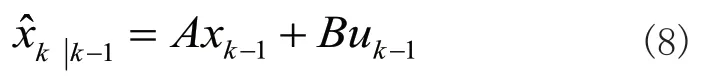
2）先验估计误差协方差：

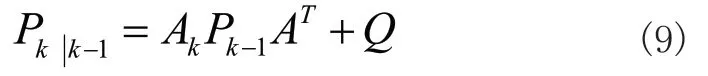
3）卡尔曼增益：

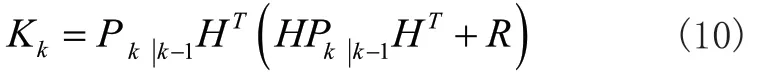
4）后验状态估计：

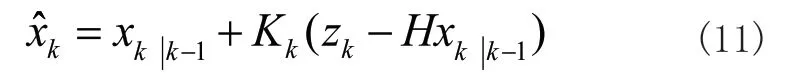
5）后验误差协方差：

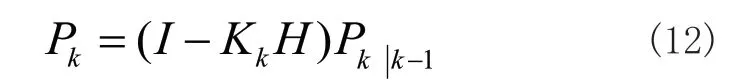
程序中使用公式Angle+=(Gyro_y-Q_bias)*dt计算出机器人某一个轴的角度，Q_bias表示陀螺仪输出值与期望值之间的误差，Angle就是系统预先估计值，然后得到观测方程；但加速度传感器采回的角度值Accel就是类似于系统中的测量值，从而得出系统的状态方程式。

Q_angle和Q_gyro各代表了系统对加速度传感器及陀螺仪传感器的信任程度。根据Pdot[0]=Q_angle-PP[0][1]-PP[1][0]计算出先验估计协方差的微分值，再把实时估计值进行线性化计算。之后计算系统估计角度的协方差矩阵PP。计算卡尔曼增益K_0和K_1，K_0用于最优预算值，K_1用于处理最优预算值的偏差和刷新协方差矩阵PP。通过进一步的计算得较真实的机器人姿态值。

4.3 PID控制器设计

4.3.1 PID控制器原理

PID因其简单的结构、较高的稳定性和便于调整的特性，得到了广泛的应用。

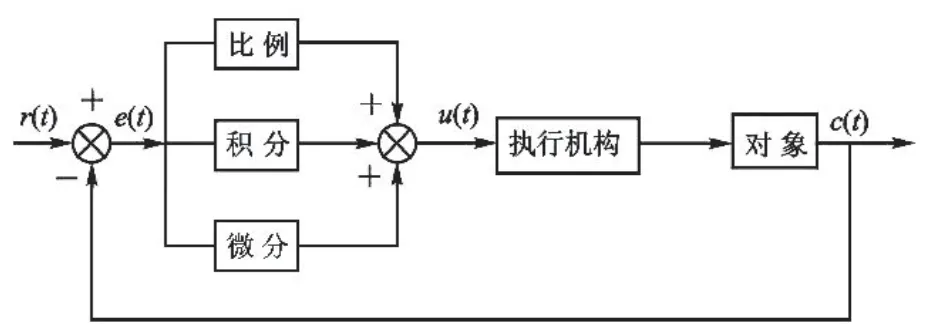
图10 PID控制示意图

上图为PID控制示意图，r(t)为输入量；e(t)为稳态误差量；u(t)为PID输出量；c(t)为实际输出量。PID的输入e(t)与输出u(t)的等式为：

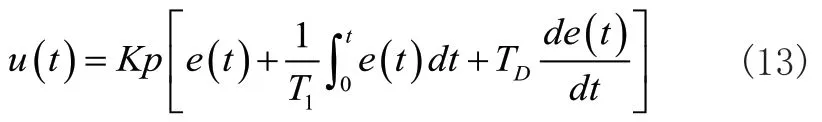
在式(13)中，Kp为比例系数；T1为积分系数；TD为微分系数，PID调节器原理简单、适应性强，实现自平衡机器人的控制方案是完全可行的。

4.3.2 PID控制器实现

在本系统中，Uk代表卡尔曼数据融合后机器人的实时倾斜角；U代表机器人直立时的倾斜角；ek为实时倾斜角度值与期望值的误差；Kp、Ki和Kd分别为比例、积分和微分环节的系数；Pp、Pi和Pd分别为比例环节、积分环节和微分环节增益量；P为PID输出量，用来控制PWM波的占空比，实现电机的转速控制。

5 基于多传感器的机器人自平衡实验

5.1 卡尔曼滤波器参数设计

机器人在调节过程中会出现轻微的抖动，通过卡尔曼滤波使抖动部分更为平缓。在对滤波器进行调试的过程中，要对卡尔曼滤波器的陀螺仪、加速度传感器的权值Q_gyro、Q_angle和卡尔曼增益R_angle设定参数，设定完成后可发送数据到上位机显示，如图11所示。

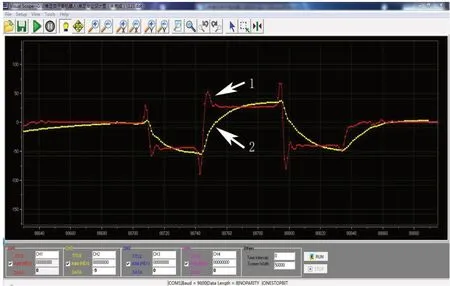
图11 卡尔曼滤波调试图

上图为卡尔曼滤波调试图，图中1表示姿态传感器原始曲线，2表示经过卡尔曼滤波后的曲线。从图可以看出，姿态值的初始曲线有很多的尖峰，噪声比较大，经过卡尔曼滤波后的波形比较的平滑，毛刺较少，可以比较精确的体现出机器人姿态的真实情况。

5.2 PID控制参数整定

通过实验，比例调节能使自平衡机器人完成动态平衡，但是响应时间较长，同时在稳定的位置不停地抖动，加入积分和微分调节使机器人的动态偏差减小，缩短调节反应时间。

图13 单足自平衡机器人PID参数整定

PID参数的整定过程：第一步调整比例系数值的大小，使机器人能直站立起来，机器人在实现站立的过程中可能会伴随着抖动现象，第二步，将比例系数值降低到设定值的70%左右，小幅度的增大微分的系数值让机器人可以稳定的平衡。

6 结束语

面向服务型行业中对移动机器人的需求，设计轮球自平衡机器人，应用多传感器实时检测机器人位姿信息，应用卡尔曼滤波算法对数据进行优化，通过整定PID控制器参数实现了该机器人的自平衡。实验结果表明该设计能使机器人在无干扰情况下实现自平衡，并通过有干扰自平衡实验表明了该控制器的鲁棒性。该设计为机器人实用化提供了新的技术和方法。

[1] 张友民,戴冠中,等.卡尔曼滤波计算方法研究进展[J].控制理论与应用.1995(05).

[2] 陆如华,徐传玉.卡尔曼滤波的初值计算方法及其应用[J].应用气象学报.1997(01)：1-3.

[3] 陆芳,刘俊.卡尔曼滤波在陀螺仪随机漂移中的应用[J].微计算机信息.2007(23)：12-16

[4] 张鹏飞,齐晓慧.基于N沟道MOS管H桥驱动电路设计与制作[J].科技信息.2012(20)：2-4.

[5] 张程.基于STM32的永磁同步电机驱动器设计[J].福建工程学院学报.2011(01)：5-10.

[6] 张志强.基于STM32的双轮平衡车[J].电子设计工程.2011(13)：19-25.

[7] 杨智,朱海锋,等.PID控制器设计与参数整定方法综述[J].化工自动化及仪表.2005(05)：25-27.

[8] 邹凌,孙玉强.基于卡尔曼滤波器的PID控制仿真研究[J].微计算机信息.2007(16)：1-20.