基于ANSYS塔机非线性变形风载跨度值的研究

王 毅，殷晨波，张首隆，蔡金群

（南京工业大学 车辆与工程机械研究所，南京 211816）

0 引言

塔式起重机具有工作效率高，回转半径大，起升高度大的特点，在民用建筑行业和工业等领域得到广泛应用，成为一种必不可少的机械装备。由于塔式起重机都是处于室外工作，受外界自然条件的影响较大，尤其是风荷载的影响。根据近20年全球塔机事故分析报告，恶劣天气所导致的塔机事故数量占总事故数量的18%。塔式起重机的安全事故，轻则塔机局部破坏，重则机毁人亡，给社会造成沉重的损失。根据不完全数据统计，在沿海台风高发地区，因为暴风侵袭而倒塌的塔机中，主肢位移失稳占事故中的30%。因此研究在大风作用下塔机的变形就成为塔机设计的重要内容。但根据现行塔式起重机设计规范GB/T13752-1992提出的计算风压设计出来的塔机并不适用于沿海台风高发地区。现提出风载作用下塔机非线性变形的计算方法，采用ANSYS数值分析法研究塔机非工作状态时，在静力风载作用下塔身的变形问题，通过选取不同跨度值进行比较，从而得出结论。

1 问题描述

现选取塔式起重机为研究对象，塔机塔身受力简图如图1所示，M为作用在塔身顶部的弯矩，包括风载、配重等引起的弯矩，F为水平力，包括小车起动、制动力，风对塔帽、臂架的作用力，N为轴向压力[1]。H为塔身总高度120m，q1，q2，…，qn分别表示各跨的均布载荷值，q1＜q2＜…＜qn。根据文献[2]给出的多点附着支撑之最佳附着间距的结论，敷设三道附墙架分别离地高度为36m，62m，89m，即图中所示A，B，C点。塔机塔身为格构式，采用1.5m×2.5m的标准节，采用等效惯性矩法求出其截面惯性矩I。

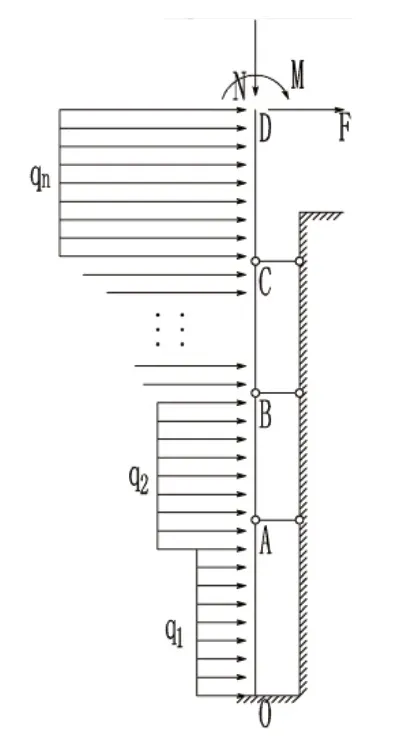
图1 塔机塔身风载荷计算简图

求解此塔式起重机塔身的位移的方法有解析法和数值法，但解析法计算需要解超越方程，计算冗杂且不方便，而ANSYS数值法只需要建立有限元模型，计算机辅助计算，所以我们采用目前工程上广泛采用的ANSYS数值法。

2 ANSYS数值法求解

垂直作用在塔机塔身纵轴线上的非工作状态风载荷按式(1)计算[3]：

式中：风力系数Cw=1.6；

计算风压pn=0.625(Khvvb)2，

计算风速vb=39.3m/s；

风速高度变化系数Khv=(h/10)0.14+0.4；迎风面积折减系数η取0.57。

四肢格构式塔身等效截面惯性矩按式(2)计算[4]：

选取跨度值分别为20m，10m，5m，0.1m，在ANSYS中建立四种情况下塔机塔身的模型，建立有限元模型的主要参数为：l1=36m，l2=26m，l3=27m，l4=31m，M=-310000N·m，F=75000N，N=250000N，塔身标准节轮廓尺寸为1.5m×2.5m，选用梁单元Beam3进行计算，弹性模量为E=206GPa，泊松比λ=0.3，截面惯性矩I=1.751×10-3cm4。

2.1 跨度值为20m时ANSYS计算

以20m为跨度值时，各跨度等压风载荷数值如表1所示。

表1 均布风载表1

根据表1在ANSYS中建立塔身模型如图2所示。

图2 塔机塔身ANSYS模型1

求解solve后提取出塔身变形图如图3所示。

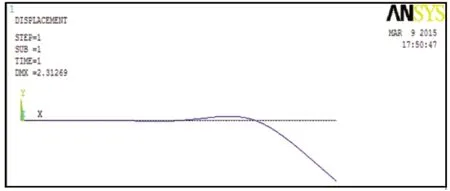
图3 塔身变形图1

得出结果，风载荷跨度值为20m时，塔身顶部位移为2.31269m。

2.2 跨度值为10m时ANSYS计算

以10m为跨度值时，各跨度等压风载荷数值如表2所示。

表2 均布风载表2

根据表2在ANSYS中建立塔身模型如图4所示。

图4 塔机塔身ANSYS模型2

求解solve后提取出塔身变形图如图5所示。

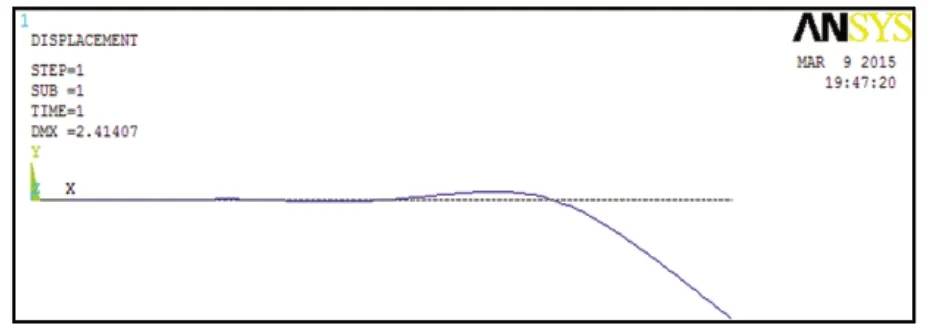
图5 塔身变形图2

得出结论，风载荷跨度值为10m时，塔身顶部位移为2.414m。

2.3 跨度值为5mANSYS计算

以5m为跨度值时，各跨度等压风载荷数值如表3所示。

表3 均布风载表3

根据表3在ANSYS中建立塔身模型如图6所示。

图6 塔机塔身ANSYS模型3

求解solve后提取出塔身变形图如图7所示。

图7 塔身变形图3

得出结果，风载荷跨度值为5m时，塔身顶部位移为2.43687m。

2.4 跨度值为0.1m时ANSYS计算

当跨度值△h=0.1m时，风载荷为：

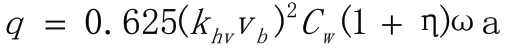
求解solve后提取出塔身变形图如图8所示。

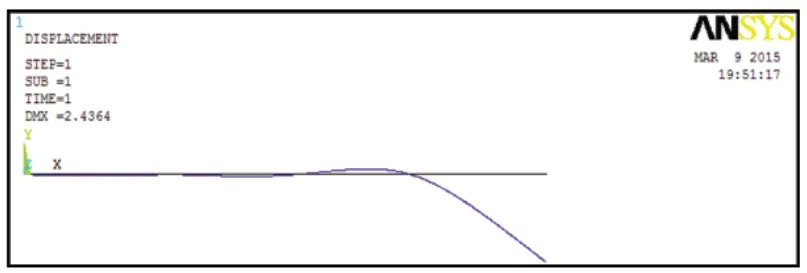
图8 塔身变形图4

得出结果，风载荷跨度值为0.1m时，塔身顶部位移为2.4364m。

3 结果分析

将本文变形计算结果及误差值列于表4中。

表4 计算结果及误差值

本文计算出来的误差采用的是相对误差法，当跨度值为0.1m时，塔身位移变形已经趋近于实际变形，故而分别将跨度值为20m，10m，5m的位移变形与跨度值为0.1m的位移进行比较，得到相对误差值。从表中的计算结果可以得出：

1）当跨度值不断减小，塔机塔身风载荷跨数越多，塔身顶部位移越接近实际情况，误差值越小。

2）第一组相对误差值为：

|2.31269-2.4364|/2.4364=5.1%＞5%，不满足工程精度需求，故而跨度值选20m不满足工程要求。

第二组相对误差值为：

|2.414-2.4364|/2.4364=0.38%＜5%，满足工程精度需求，故而跨度值选为10m满足工程要求。

第三组相对误差值为：

|2.43687-2.4364|/2.4364=0.02%＜5%，满足工程精度需求，故而跨度值选为5m满足工程要求。但是跨度值选为5m的时候，理论计算相对复杂，计算量是跨度值为10m的两倍，故而跨度值选择10m。

4 结论

本文采用ANSYS数值法求解了塔式起重机塔身的非线性变形问题，通过比较跨度值为20m，10m，5m，0.1m的塔身位移变形情况，可以得出以下结论：

1）在非工作情况下，塔式起重机受大风侵袭，塔身所受风载荷跨度值越小，分段越密集，塔顶位移精度越高。

2）在计算非工作状态时塔机所受的风载荷，可沿塔身高度划分成10m高的等风压段，以各段中点高度处风压为该段等风压值。

但本文研究的风载是垂直于塔身纵轴线上，实际情况下风的方向是与纵轴线有一定角度的，这种情况下的塔身位移需要进一步研究。另外，塔机依附的建筑物对作用在塔身上的风载也是有很大影响的，在建筑物环境下塔身上的风载跨度值还需要做进一步的理论和试验研究。

[1] 王文浩,叶学华,毛晓菲,高崇仁,苟文选.风载作用下塔式起重机非线性变形的近似计算法[J].中国工程机械学报,2013(11)：415-419.

[2] 罗冰,陆念力,夏拥军.塔式起重机合理附着间距与塔身最大外伸高度的确定[J].工程机械,2006(10)：12-15.

[3] GB/T13752-1992塔式起重机设计规范[S].北京.中国标准化出版社,1993.

[4] 陆念力,王佳,兰朋.格构式构件整体稳定性分析的等效惯性矩法[J].建筑机械,2008(08)：79-84.