引入先验知识的燃油加热器系统神经网络辨识
臧玉萍,张 洋,孙 博
ZANG Yu-ping1,ZHANG Yang1,SUN Bo2
(1.长春工业大学 人文信息学院,长春 130122;2.长春工业大学 基础科学学院,长春 130012)
0 引言
独立式汽车燃油加热器,是一种用于对工作在低温条件下的汽柴发动机进行预热的小型燃油内燃机系统。该系统一般由燃油供给、电控点火、助燃空气供给、燃烧及热交换、水循环、暖风循环、电控单元等主要部分构成。对加热器的控制目标之一是通过调整油泵的燃油供给量和风机的助燃空气供给量使发动机冷却液温度按预定的曲线变化。加热器-负载系统是一种具有滞后、系统外部不确定扰动引起时变等特征,且难以建立确定数学模型的被控系统,由此控制模型的设计必须解决系统模型在线辨识的问题。
系统辨识问题本质上是一个优化问题。传统辨识算法的基本思想,是通过建立一个与系统输入和输出响应相关的参数模型,将辨识问题转化为模型的参数识别问题,典型方法如最小二乘法、梯度校正法、极大似然法等。此类方法,在对具有不确定参数的线性、时不变系统的辨识和自适应控制问题中取得了很大的进展,但对于非线性、时变、滞后系统则还很难实行有效的辨识和自适应控制[1]。
神经网络建模方法的一大特点是“黑箱”特性,即不需要对系统的内部结构、动力学特性做任何分析,只需要知道输入输出即可[2]。神经网络用于系统辨识的本质,是选择一个合适的神经网络模型来逼近实际系统。辨识过程中,通过直接学习系统的输入/输出数据,使误差函数达到最小,从而归纳出隐含在系统输入/输出数据中的关系,从而完成对原系统的辨识。
1 SISO系统三层前向神经网络辨识器
1.1 神经网络辨识器拓扑结构
具有单输入输出关系的SISO(Single Input Single Output,单输入单输出)系统是一类工程中普遍存在的控制对象。设具有此特征的SISO系统:
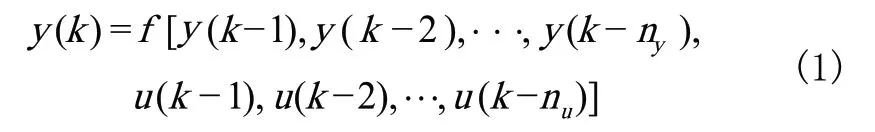
式中,u(k)、y(k)为由第k次采样得到的系统输入和输出;nu和ny为u和y的阶次;f[.]为非线性函数。
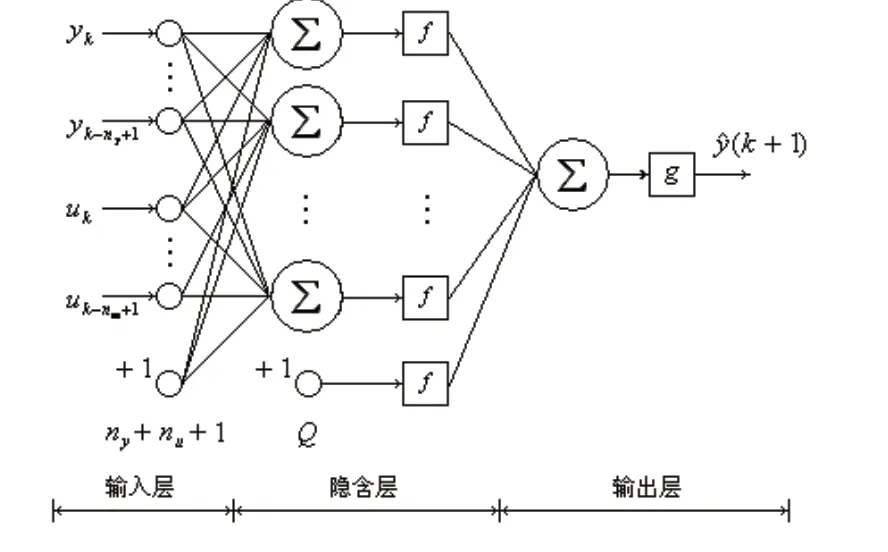
图1 SISO系统三层前向神经网络辨识器拓扑结构图
络辨识器模型NNI的输入-输出关系可表述为:

式中,k为采样序号,k=0,1,2…;

f[.],g[.]分别为隐含层、输出层传输函数,且有:
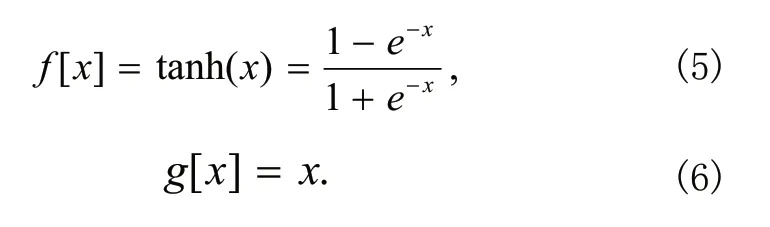
1.2 三层前向辨识网络权值系数调整算法
式(2)~式(6)给出的三层前向辨识器模型中的权值/阈值系数可借助反向传播学习算法确定[1]。修正权值系数的过程本质上是一个搜索过程。基于理想辨识模型将使系统输出y和辨识器预报输出之间误差最小的思想,及辨识准则:

可建立指标函数:
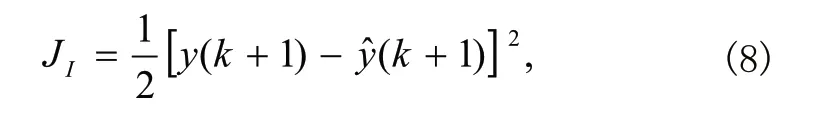
并由此得到权值系数的调整算法:
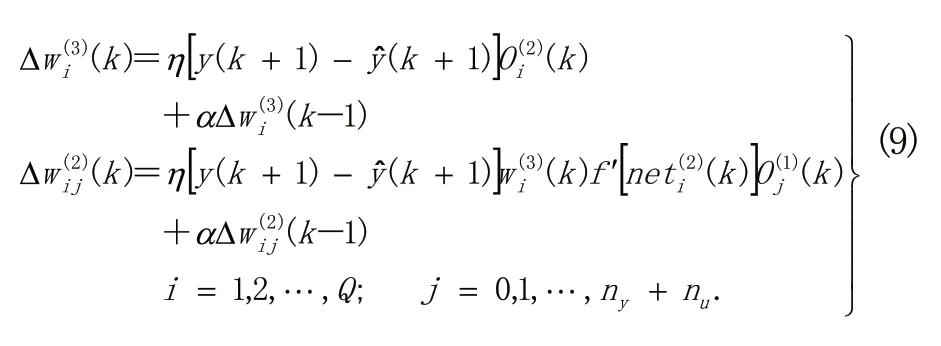
式中,η∈[0,1]为学习速率;α∈[0,1]为动量系数。引入动量系数是为了加快搜索过程,使其快速收敛于全局最小。
2 LLYCO-30KW加热器系统神经网络辨识器设计
LLYCO-30KW型加热器是雷克汽车供暖有限公司生产的独立式燃油加热器,实验研究表明,该加热器在负载不同的情况下,开环响应曲线表现出明显的S形特征,负载不同,滞后时间不同,系统特性随温度的变化具有明显的缓时变特征,本文以LLYCO-30KW型加热器为对象设计神经网络辨识器。
2.1 辨识器网络输入设计
式(2)~式(6)以及图1给出了SISO系统三层前向辨识器的基本理论构架,工程实践中需进一步确定网络输入层向量和隐含层神经元数量。
对于如式(1)给出的SISO系统,根据系统输入u和输出y的阶次nu和ny确定输入向量元素数。对于响应曲线具有明显S形特征的一类系统用三阶函数加以描述。记辨识器输入层输入向量为p,输入u的阶次为nu,输出y的阶次为ny,总节点数为nI,则有:

式中,y(k)为第k次采样得到的系统输出值;u(k)、u(k-1)、u(k-2)分别为第k、k-1、k-2次采样得到的系统输入值。
2.2 辨识器隐含层神经元设计
辨识网络隐含层神经元设计问题,与问题域密切相关,目前还没有一种可行的理论方法可借鉴,实践中通常是采用经验和实验的方法。对于本工作所涉及的高阶非线性研究对象而言,一般认为如下一些原则对隐含层拓扑结构设计具有借鉴意义:
神经元数量不少于输入数。
增加神经元数量有利于提高预测精度,但同时会由于结构复杂度的增加而增加计算时间,降低时间效率。
减少神经元数量会加大预测误差,同时也会由于预测值不能很快的收敛于目标值而增加计算时间,降低时间效率。
过多的神经元数量会增加过拟合的风险,降低鲁棒性。
基于上述考虑,本工作针对辨识网络隐含层设计问题,对含有不同隐含层神经元数的辨识网络进行了实验研究。实验结果表明,由3~5个神经元构成的隐含层网络,均可对本工作所对的目标系统实现有效的辨识;其间的区别在于简单的隐含层结构(如3神经元模型)有利于减小初始误差,但5神经元模型的辨识收敛速度则明显优于3神经元模型。而更复杂的隐含层结构,从各方面考虑都是不利的。
2.3 先验知识引导模型与基于先验知识的网络权值系数初始化
神经网络辨识器工作过程中,首先需要对网络权值系数进行初始化赋值[3,4]。通常情况下,可采用一组非零的随机数作为网络权值系数的初值。对被测目标系统的辨识、黑箱建模过程的本质是在一组由无穷多个备选模型组成的解空间中搜索出一个次优解(或满意解)。随机初始化权值系数的方法,相当于在解空间中随机选取一点作为搜索起点。显而易见,由随机起点收敛到接近次优解(或满意解)所在位置需要一段时间,而若能以接近次优解(或满意解)所在位置作为搜索起点,无疑会减少搜索步次,加快收敛速度,进而提高辨识器的时间效率。而对于实时在线辨识的应用目标而言,时间效率的提高有着重要的意义。
一种解决此问题的思想是借助于先验知识选择一组参数作为辨识网络的初始值。加入先验知识相当于减小了神经网络函数类的VC维数[5],在神经网络中使用任何一种先验知识都能改进网络的泛化能力。与此同时,引入先验知识后的神经网络,既可以满足一定的过程特性(增益、单调、凸性等),也能保证可靠的安全性(避免零增益和增益反转)[6]。考虑到导致加热器系统模型变化的主要原因为外部环境条件的变化,而一般情况下此时变过程为一缓变过程,由此可以利用前次辨识得到的系统模型参数作为先验知识初始化网络权值系数。可以预见,此权值系数初始化模型在最不利的情况下等价于随机数初始化模型;而在一般多数情况下将表现出更优良的时间效率。
基于上述思想,本工作在系统辨识器中增加了一个用于保存前次辨识得到的系统模型参数的知识库模块,作为先验知识引导本次辨识网络权值系数。知识引导学习算法的系统辨识器框图如图2所示。
图3为5神经元模型在两种初始化条件下辨识性能的比较,其中图3(a)为采用随机算法初始化网络权值系数的辨识误差曲线,图3(b)为采用先验知识引导算法初始化网络权值系数的辨识误差曲线。分析实验结果可见:基于先验知识的网络权值系数初始化模型对辨识器性能有明显改善作用;知识引导模型的最大辨识误差降低至随机模型的30%左右;辨识响应速度也有所提高。
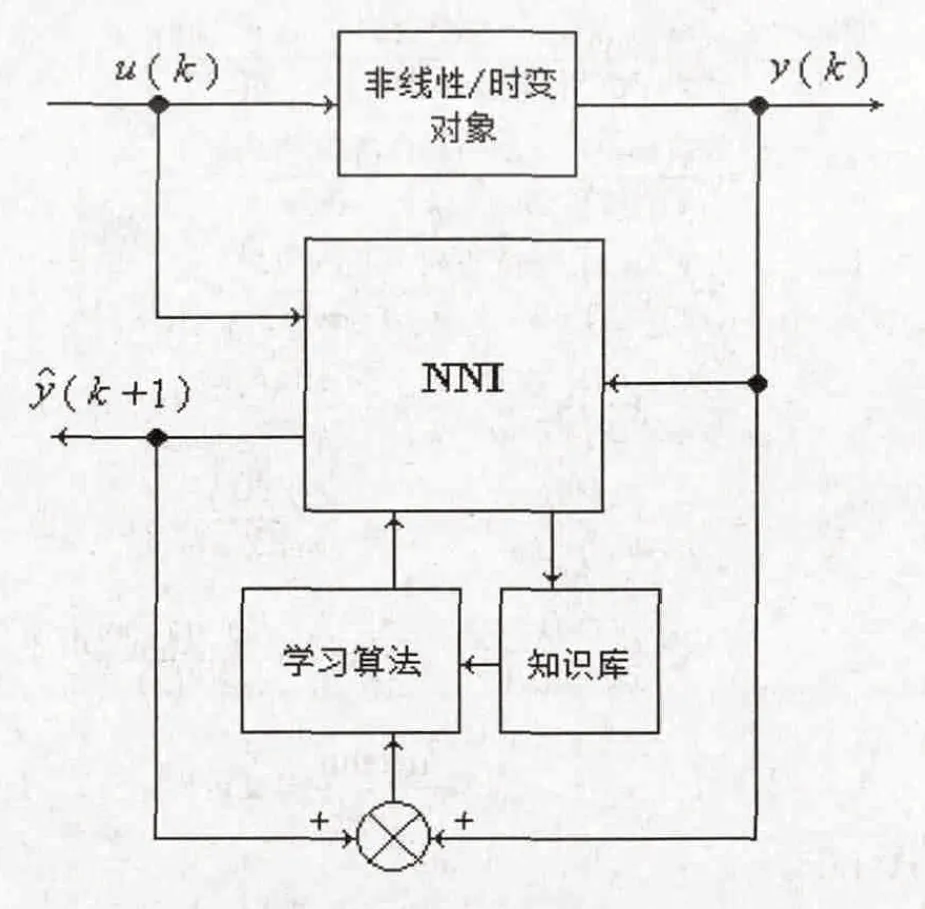
图2 知识引导学习系统辨识器结构框图
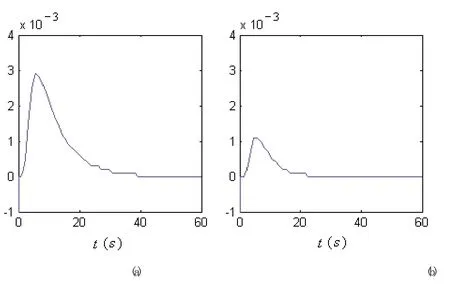
图3 两种初始化条件下5神经元结构辨识器辨识性能比较
其中:(a)为采用随机算法初始化网络权值系数的辨识误差曲线;(b)为采用先验知识引导算法初始化网络权值系数的辨识误差曲线。
2.4 辨识网络拓扑结构设计
式(2)~式(6)与图1给出的SISO系统三层前向神经网络辨识器的输出为第k+1次循环时系统的预报输出实践中还需要以的形式(即第k+1次循环系统预报输出对第k次采样得到的系统输入值的偏导数)作为系统输出,由式(2)~式(6),可导出的计算式:
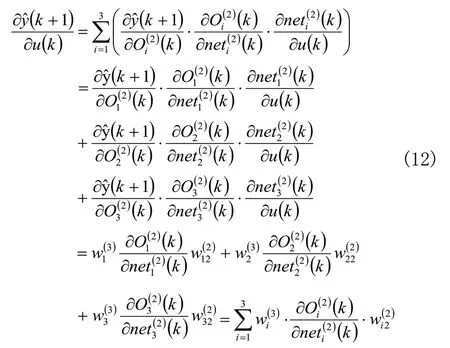

在前述讨论基础上,可构建加热器系统SISO三层前向神经网络辨识器NNI,拓扑结构如图4所示。为方便后续仿真计算起见,图中采用了Simulink仿真器符号系统。其中:
隐含层由5个神经元构成IW为隐含层5×4权值系数矩阵。b1为隐含层5×1偏值系数向量。n1为隐含层5×1累加器输出。f[.]为式(3)~式(7)所定义的隐含层双曲正切传输函数。a1为隐含层5×1输出向量。
输出层由1个神经元构成。IW为输出层1×5权值系数矩阵。b2为输出层1×1偏值系数向量。n2为输出层1×1累加器输出。g[.]为式(3)~式(8)所定义的输出层传输函数。为辨识器预报输出,1×1输出向量。为第k+1次循环系统预报输出对第k次采样得到的系统输入值的偏导数,1×1输出向量。
2.5 辨识器在线建模算法设计
辨识器在线建模算法如下:
调入知识库,读取:输入层节点数nI;隐含层节点数Q;学习速率η;
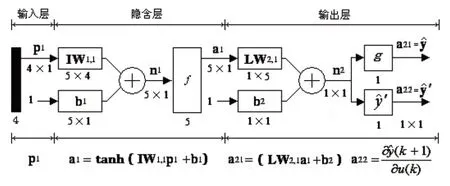
图4 加热器系统SISO三层神经网络辨识器拓扑结构
动量系数α;隐含层权值系数矩阵IW,偏置系数向量b1;输出层权值系数向量IW,偏置系数向量b2;采样序号k=0;输入向量初始化p1=(0,0,0,0);
读当前时刻输入/输出采样值u(k),y(k);
输入层输入向量p1赋值,
计算隐含层累加器输出:
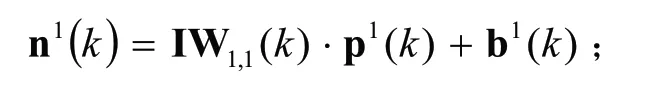
计算隐含层传输函数输出:
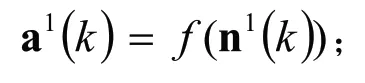
计算输出层传输函数输出:

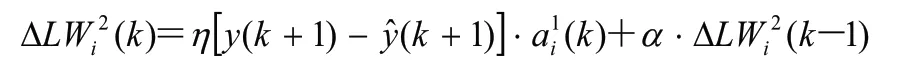
修正隐含层权值系数向量:

读停止指令;若指令继续,跳转至下一步;若指令停止,跳转至式(13);
采样序号k=k+1;
返回至式(3);
保存IW、LW至知识库;
退出。
3 辨识器Simulink仿真实验研究
利用MATLAB-Simulink仿真器平台,对3.3节加热器系统辨识模型和3.5节在线建模算法进行仿真调试。系统辨识器NNI仿真结果如表1所示,仿真曲线及仿真误差曲线如图5所示。
图5左图为燃油加热器系统辨识Simulink仿真曲线。图中阶跃线为单位阶跃信号,曲线为加热器传递函数输出曲线,*号线为辨识器辨识输出。右图为燃油加热器系统辨识Simulink仿真误差曲线。
分析NNI仿真数据可知:

表1 加热器系统辨识器Simulink仿真结果
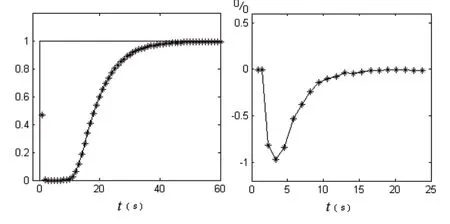
图5 燃油加热器系统辨识Simulink仿真曲线
NNI辨识器可以很好的实现对燃油加热器的系统辨识任务,最大辨识误差不大于1%,优于加热器设计的精度要求。
NNI辨识器具有良好的响应特性。辨识误差不大于1%的响应时间不大于3秒,优于加热器设计对缓慢时变系统实时在线辨识建模的响应速度要求。
4 结论
1)采用神经网络对燃油加热器系统进行在线辨识,设计了一种基于三层神经网络模型的系统辨识器NNI。NNI以由第k次采样得到的被控系统的输入、输出u(k)、u(k-1)、u(k-2)、y(k)作为辨识器的输入,隐含层采用5神经元结构和双曲正切函数作为传输函数,输出层采用单神经元结构和线性传输函数,采用了基于反向传播学习算法的网络权值系数调整算法。实验结果表明,NNI辨识器最大辨识误差不大于1%,优于加热器设计的精度要求;NNI辨识器具有良好的响应特性,辨识误差不大于1%的响应时间不大于3秒,优于加热器设计对缓慢时变系统实时在线辨识建模的响应速度要求。前向神经网络辨识器NNI是解决具有三阶非线性、时变不确定性、纯滞后等特征的系统辨识问题的有效方法。
2)构建了知识引导学习模型,采用了先验知识引导下的权值系数初始化策略,从而加快了搜索过程收敛于满意解的速度,更有利于实现对控制对象的实时在线辨识和建模。
[1]Martin T.Hagan,Howard B.Demuth,Mark H.Beale.神经网络设计[M].北京:机械工业出版社,2002.
[2]薛福珍,柏洁.基于先验知识和神经网络的非线性建模与预测控制[J].系统仿真学报,2004,16(5),1057-1063.
[3]Martin T.Hogan,Howard B.Demuth,Mark H.Beale.Neural Ntwork Design[M].北京:机械工业出版社,2002.
[4]Theodoridis,Koutroumbas.Pattern Recognition(2nd Edition)[M].北京:电子工业出版社,2004.
[5]Abu-Mostafa Y S.Hints and VC dimension[J].Neural Comut.1993,5:278-288.
[6]娄海川,苏宏业,谢磊.融合过程先验知识的递归神经网络模型及其应用[J].化工学报,2013,64(5):1665-1673.

